新工科背景下线性代数教学改革与探索

2020-10-21杨威高淑萍陈怀琛李兵斌

高教学刊 2020年5期

杨威高淑萍陈怀琛李兵斌

摘要：以国家精品在线开放课程《实用大众线性代数》为例，根据新工科背景下人才培养的成果导向理念，对线性代数教学进行改革，通过课程体系简洁化、教学内容形象化、应用实例多样化、MATLAB深入化及信息技术全面化等教学理念的应用，使得线性代数学以致用，培养了学生运用理论知识解决实际问题的能力。

关键词：新工科;成果导向;线性代数;MATLAB;MOOC

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2020）05-0008-05

Abstract： Taking "Applied Popular Linear Algebra with MATLAB" of the national quality MOOCs as an example. According to the OBE concept of personnel training under the background of emerging engineering education， the teaching of linear algebra is reformed. By using the teaching methods of concise curriculum system， visualization of teaching content， diversification of application examples， deepening of MATLAB and comprehensiveness of information technology， it is trained ability to solve practical problems by using theoretical knowledge.

Keywords： emerging engineering education（3E）; outcome based education（OBE）; linear algebra; MATLAB; MOOCs

一、新工科背景下人才培养新理念

随着我国经济转型、国家战略的实现及新经济快速发展，对新型工科人才需求增加，2016年，新工科概念首次提出，2017年初正式拉开了全国范围工程教育改革的帷幕。新工科的人才培养理念是用成果导向替代学科导向，成果导向又由以学生为中心、反向设计和持续改进三个理念组成。以学生为中心的教学内容主要取决于学生学什么，教学方法主要取决于学生怎么学，教学评价主要取决于学生学得怎么样。教学本质就是“教学生学”，教学生“乐学”、“会学”、“学会”。教学目的是：“教为不教，学为会学”。反向设计理念是针对传统的正向设计而言的，反向设计是从需求开始，由需求决定培养目标，再由培养目标决定毕业要求，再由毕业要求决定课程体系。成果导向是反向设计、正向实施，这时“需求”既是起点又是终点，从而最大程度上保证教育目标与结果的一致性[1]。

二、新工科背景下线性代数教学存在的问题

线性代数是所有高校工科专业的一门重要基础课程，同时它也是工程数学中最重要的组成部分，它还是学生学习后续课程的前提和工具。随着新技术的高速发展，线性代数也渗透到工程、经济、信息、社会等各个领域。在新工科的教育改革中，很多高校对公共基础课程都进行了压缩。以西安电子科技大学为例，线性代数课程从原来的56学时压缩到40学时，课时减少了近1/4。然而線性代数具有高度抽象、逻辑严密、符号独特等特点，因此很多初学者觉得这门课难理解;另一方面，新工科的人才培养新理念要求培养适应未来工程发展需求的具有可持续性竞争力的应用型工程人才[1]。线性代数内容抽象、课时又减少，而对人才培养又提出了新的要求，在这样的新工科背景下，线性代数课程的教学改革就显得非常重要。

目前，大多国内高校数学类课程教学模式落后，以教师为中心的现象仍然普遍存在，课堂填鸭式教学让学生苦不堪言。教学内容陈旧，缺乏应用案例，没有把MATLAB与线性代数相结合。教学评价单一，仅仅通过期中和期末考试来评定学生成绩。这些都严重影响了学生创新思维的培养。

三、新工科背景下线性代数教学改革

美国在1990年对线性代数课程改革提出以下建议：1.教学大纲必须响应其他学科的需求，在学生后续课程的学习中能感受到线性代数的作用。2.线性代数应从具体实际例子出发引出概念和理论。3.计算机技术必须应用在线性代数教学中[2]。

从2005年开始，西安电子科技大学对线性代数课程进行了长期、持续的改革与探索，教育部“使用信息技术工具改造课程项目”——用MATLAB和建模实践改造工科线性代数子项目带动了全国19所大学进行改革试点，其改革成果得到教育部数学教指委的高度认可，首批国家精品在线开放课程《实用大众线性代数》就是持续改革的成果之一[3]。

（一）课程体系简洁化

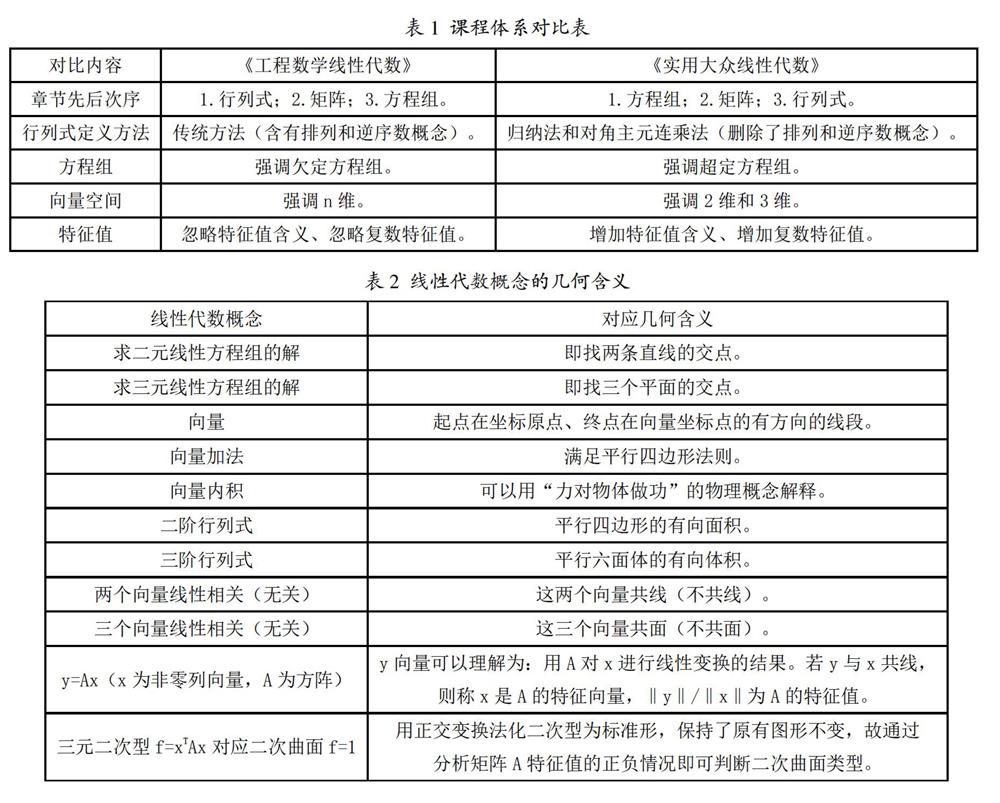
根据新工科人才培养的成果导向理念，课程体系的制定要从人才培养的需求入手，而新工科背景下，需要大量的可持续竞争力的应用型工程人才。《实用大众线性代数》以方程组为主线，从方程组出发，引出矩阵的定义、矩阵运算及应用、行列式、向量空间及特征值特征向量。表1给出了它与同济大学数学系编写的《工程数学线性代数》（第六版）在课程体系上的差异[4][5]。该课程删减了一些工程中不常用的复杂概念，增加了一些工程应用内容，降低了课程难度和理论门槛，减少了课时量，使大一学生及工作多年的工程技术人员都能容易掌握。课程体系的建立与新工科背景下人才培养理念相吻合。

（二）教学内容形象化

新工科人才培养强调了以学生为中心，教师考虑的最重要的问题是“学生怎样能学好”，这就要求发挥教师的主观能动性，把线性代数抽象概念形象化是教师的首要任务。

1. 几何概念全方位引入

线性代数与几何紧密相关，线性代数许多概念、公式和定理都可以得到几何意义的解释，另一方面，线性代数理论也为几何问题提供了有效的解决方法。所以把几何含义融入线性代数教学中，首先可以提高学生学习兴趣，帮助学生了解相关概念的背景;其次可以把抽象问题形象化，使学生在形和数的统一中进一步体会到抽象概念的内涵，从而培养了学生抽象思维能力和解决实际问题的能力[6]。

《实用大众线性代数》课程全方位地把几何概念引入到课程各章中，表2给出课程涉及的部分几何含义[4]。

2. 类比思想的应用

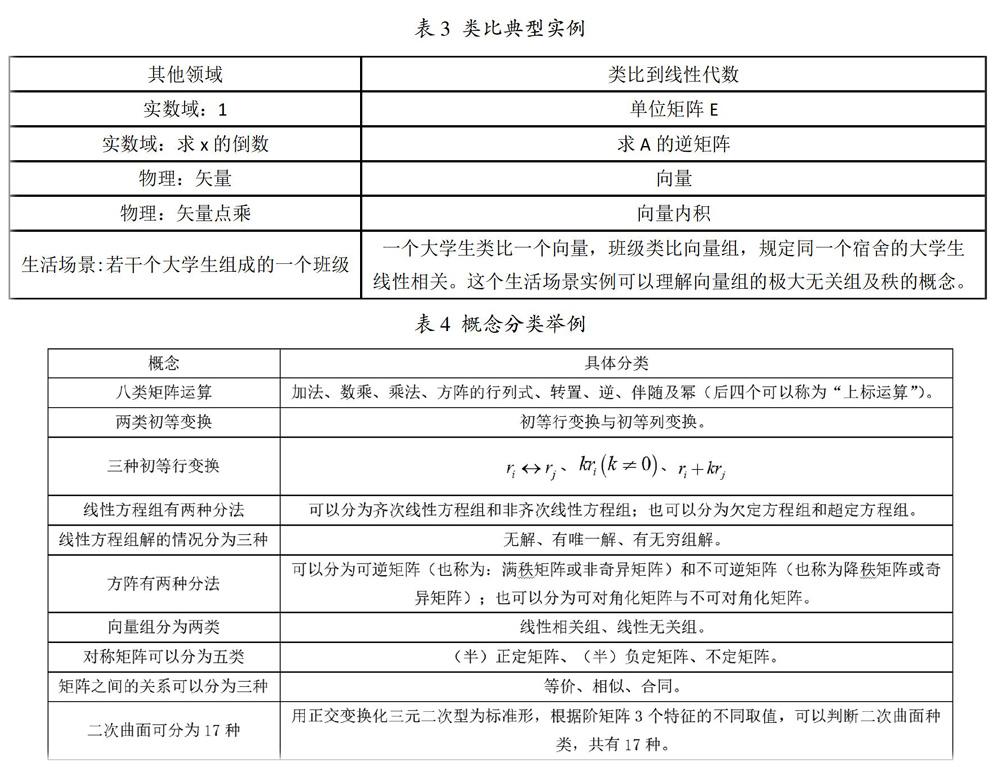
适当地运用类比思想可以让学生的思维从熟悉的知识向新知识转移，从而更容易掌握新知识[7]。在线性代数的教学中类比思想分为两类。一类是线性代数本身内容之间的类比，比如用低阶行列式类比高阶行列式，用低维向量类比高维向量等，这种类比实质上就是由简单到复杂、由特殊到一般的思想方法。另一类是其他知识和线性代数知识间的类比，表3给出了几个类比的典型实例。

3. 分类方法的应用

分类是一种很好的形象化教学方法。通过分类，学生可以更好地理解和记忆线性代数繁多概念和公式，也更容易从中发现规律和解决问题的方法。表4对线性代数的一些概念进行了分类[8]。

4. 列表与概念图的应用

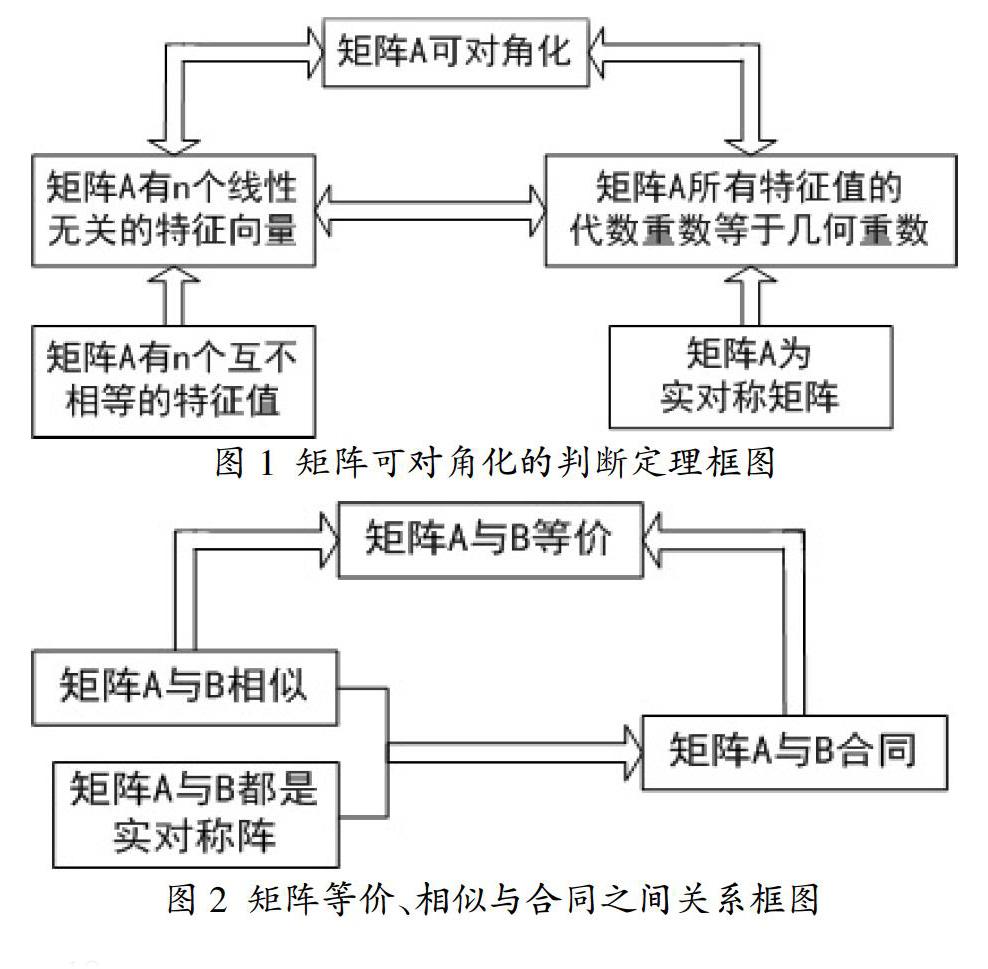
列表和概念图是形象化教学的又一方法。从心理学角度出发，人对图表的记忆力会比单纯的文字强很多，图表可以将细碎的知识以简单的形式有组织有次序的表达出来。一个有效的列表或概念图能够把人脑中隐性知识显性化、可视化，可以开发学生智力，培养学生的创新能力。图1给出了矩阵可对角化的判断定理框图，图2给出了矩阵等价、相似与合同之间的逻辑关系框图。

5. 突破思维惯性

新工科人才培养强调了以学生为中心，教师就必需充分了解学生，学生“学会了”、“会学了”才是好的教学效果。对于刚进大学的学生而言，必须突破原有的数学思维惯性，才能很好的掌握线性代数知识。突破思维惯性最好的方法之一就是“错讲教学法”和“错例解析法”。“错讲教学法”是教师课堂设计一个错误的结论，让学生分析讨论;“错例解析法”是把学生出错题目作为例题讲解讨论。表5给出矩阵运算中最容易出错的问题[8]。

（三）应用实例多样化

新工科成果导向理念的核心之一就是反向设计，从人才“需求”出发来制定教学环节，在新工科背景下，需要大量的工程实用人才，所以线性代数的应用就显得极为重要。

1. 从应用实例出发引出线性代数概念

教师应该广泛地联系生活场景及其他相关学科，从学生熟悉和感兴趣的问题出发，引出线性代数概念[9]。比如，可以从一些生活场景实例引出矩阵加法和乘法运算概念;可以从力对物体做功的物理知识引出向量的内积运算;可以从0没有倒数引出奇异矩阵的概念。

2. 制作后续课程相关应用实例

线性代数是很多后续课程的基础和工具，学生通过了解线性代数在后续课程的应用，不仅可以提高学习线性代数的兴趣，同时也为后续课程的学习打下了基础。《实用大众线性代数》课程针对：电路、力学、信号与系统、数字信号处理、空间解析几何、测量学、动漫技术、自动控制系统、机器人运动学、文献管理及经济管理等后续课程给出了相关应用实例[4]。

3. 制作不同专业背景的应用实例

根据不同学科和专业的学生，引导学生提出和学科专业相关的实际问题，分析并讨论用线性代数来解决问题的方法，可以培养学生的创新性思维能力[6]。例如可以为经济管理专业学生讲解生产成本、管理决策的例子;为信息工程专业学生讲解信息编码的例子;为计算机专业学生講解动漫技术的例子等。

《实用大众线性代数》课程给出了大量工科后续课程和不同专业的应用实例29个，视频总时长300余分钟，其比例占到课程总内容的1/3[3]。

（四）MATLAB应用深入化

线性代数存在繁琐的矩阵运算，随着矩阵阶数的增加其运算量急剧增加，尤其在解决实际问题的数学建模过程中，计算机的应用就势在必行。目前，MATLAB软件已经流行于线性代数的教学和学习中，几个简单的MATLAB命令就能实现线性代数的各种运算。学生可以利用MATLAB实现矩阵模型的建立和求解，同时解决实际问题的能力也得到了提高[10]。

另一方面，MATLAB还有很好的绘图显示功能，教师可以利用MATLAB编写课件和动画，使线性代数教学变得更加生动，不仅提高了学生的学习兴趣，而且加深了对概念的理解，同时也提高了学生的理解能力和思维能力[6]。

以下分别给出三个利用MATLAB软件计算并绘制图形的实例，图形非常形象地反映出线性代数概念的几何含义。图3给出一个二元非齐次线性方程组无解的示意图，并用最小二乘法求得一个近似解（用“*”表示）;图4给出一个三元非齐次方程组有唯一解的示意图;图5给出四个二次型对应的二次曲面，从图5中可以非常形象的理解正定、负定、半正定及不定的概念[10]。

《实用大众线性代数》课程把MATLAB软件深入应用到整个课程的应用实例中，针对每一个应用实例，都给出了用MATLAB软件实现线性代数运算的程序，这大大地提高了学员数学建模的能力[4]。

（五）信息技术全面化

新工科背景下的教育教学改革内容之一就是信息技术与课程深度融合。所谓信息技术与课程整合，是在移动互联网技术、数字技术和人工智能技术等新一代信息技术支持下，将新技术创造性集成融合于课程和教学，以追求学生自主、合作、探究和高效学习为目的的教育信息化过程。信息技术与课程的融合从初级到高级分别为：动态的课堂演示、单机的数学实验和全交互的网络教学。慕课（MOOC）、微课（SPOC）等在线课程形态的出现，颠覆了传统的教育观、教学观和学习观，引发了教学方式和学习方式的深度变革。作为教师，应该把各种信息化技术应用到线性代数的教学中，以提高学生学习兴趣，培养学生学习能力。

《实用大众线性代数》MOOC提供了：视频、图片、课件、动画、论文、程序、作业及试题等各种了教学资源，并且从内容上和难易程度上都进行了分类，学员可以自由选择，提高了学习效率和效果。其次，学员可以根据自身情况安排学习计划，使慕课学习与平时的学习和工作并行不悖。慕课的开放性对学员也有很强的吸引力，学员可以快速、灵活、高效、免费地学好线性代数知识。

四、结束语

根据新工科的人才培养理念，线性代数的教学目标应该根据学生在后续课程和今后工作与研究中的需要来制定，所以课程体系简洁化、应用实例多样化及MATLAB深入化就成为线性代数教学改革的重点。教学方法和教学手段要以学生为中心展开，所以教学内容形象化、信息技术全面化不仅提高了学生学习兴趣，发挥了学生学习主动性，同时也培养了学生自主学习能力。

《实用大众线性代数》于2017年12月获国家首批精品在线开放课程。从2016年10月至今已经在中国大学MOOC平台连续播放六期，学员总数达七万余人。根据新工科成果导向新理念，教学效果的评价是由学生来决定，以下给出了该MOOC的部分学员评价。

“我觉得应用才是大学里每一门课程的教育目的，同时也觉得中国的大学教育真的应该改革了，希望以后更多人能在这门课程上受益。”

“线性代数有了MATLAB才真正把理论和计算相融合，这门课合适工程应用的人群。”

“我一直认为数学必须结合计算机才是最正确的学习和教学方法，这样才更能将抽象的地方形象的表现出来。”

“工程数学立足实践，讓人会用才是根本。毫不夸张的说，这门课为我开启了一个新世界。”

“相逢恨晚！之前从未听过如此实用接地气的线性代数，作为机械工程从业者对老师表示感谢”。

以上评价说明本MOOC真正做到了学以致用，提高了学生运用理论知识解决实际问题的能力，为培养可持续性竞争力的应用型工程人才奠定了基础。

参考文献：

[1]姜晓坤，朱泓，李志义.新工科人才培养新模式[J]高教发展与评估，2018，34（2）：17-24.

[2]朱琳，蒋启芬.国外线性代数的教学研究述评[J].数学教育学报，2018，27（1）：79-83.

[3]杨威，高淑萍，陈怀琛.慕课背景下MATLAB与线性代数应用的融合[J].高等数学研究，2019，22（3）：60-62.

[4]陈怀琛.实用大众线性代数（MATLAB版）[M].西安：西安电子科技大学出版社，2014.