玻璃幕墙清洗机器人爬行机构动力学分析

贺利乐，黄天柱，刘小罗

（西安建筑科技大学机电工程学院，陕西 西安 710055）

1 引言

玻璃幕墙清洗机器人主要用来对高楼垂直壁面进行清理，随着对清理自动化程度及安全性的要求的提高，玻璃幕墙清洗机器人的新型机构与动态稳定性受到了广泛关注。衣正尧等对一种新型船舶壁面除锈爬壁机器人建立了动力学模型，并运用模糊优化理论对模型进行了优化和仿真[1]；徐亚茹等建立了双腔体吸附、轮式爬壁机器人的解析动力学模型并建立了动力学方程[2]；香港城市大学研制了一种清洗爬壁机器人，其采用的是履带式结构，使用吸盘和履带的配合完成机器人的吸附和运动[3]；德国马格堡弗劳恩霍费尔研究所研制了一种清洗建筑物玻璃的机器人，该机器人的移动是通过水平和竖直轨道而实现的[4]；上海大学研发了一种框架式的壁面爬行类机器人[5]，这种机器人由多层可以相对运动的框架构成，在框架上安装有吸盘，吸盘的交替吸附可实现机器人的运动。设计了一款双轮驱动多吸盘的玻璃幕墙清洗机器人爬行机构，建立了其力学模型和动力学模型，并进行了动力学仿真分析，为机器人的结构优化和运动控制奠定了理论基础。

2 玻璃幕墙清洗机器人爬行机构的设计

所设计的玻璃幕墙清洗机器人爬行机构，如图1 所示，包括1—吸附机构（两组）、2—垂直运动机构（两组）、3—本体支架、4—悬架机构（两组）、5—驱动轮（两组）。吸附机构1 连接垂直运动机构2，垂直运动机构2 连接本体支架3，本体支架3 连接悬架机构4，悬架机构4 连接行走轮5。该双轮驱动多吸盘的结构可使得机器人具有在平滑玻璃幕墙快速平稳移动的能力，同时两组吸附机构配合悬架机构可使得机器人具有跨越窗框等障碍的能力。

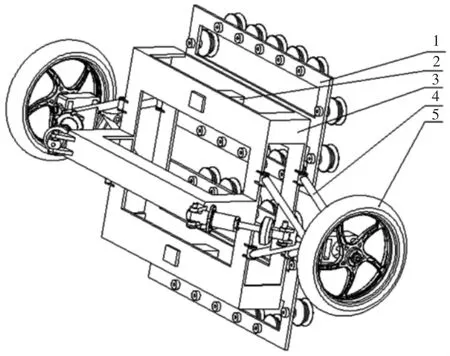
图1 机器人爬行机构Fig.1 Crawl Structure of the Robot

3 静风载下机器人爬行机构动力学建模

3.1 最不利静风载分析

首先要确定最不利静风载的大小和方向，然后才能对静风载下玻璃幕墙清洁机器人爬行机构进行静力学分析。通过测量各投影面的面积，如图2 所示，可得模型的外形投影尺寸参数为：Sx投影=0.172m2，Sy投影=0.104m2，Sz投影=0.055m2。

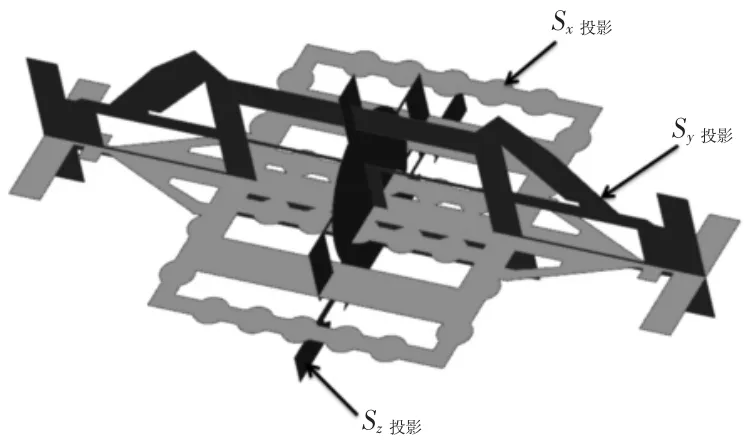
图2 模型的外形投影Fig.2 Shape Projection of the Model

查阅《GB 50009-2012 建筑结构荷载规范》[6]，可得：

式中：ϖk—风荷载标准值（kN/m2）；βz—高度z 处的风振系数；μs—风荷载体型系数；μz—风压高度变化系数；ϖ0—基本风压（kN/m2）[7]。

风振系数βz可按下式计算，

式中：g—峰值因子，可取2.5；I10—10m 高度名义湍流强度，西安地区可取0.39；Bz—脉动风荷载的背景分量因子，可取1.2；R—脉动风荷载的共振分量因子，可取1.2[8]。计算可得风振系数 βz=4.66。

对于城市建筑，风荷载体型系数μs可取0.96。

风压高度变化系数μz对应200m 高楼，可取1.92。

对于基本风压ϖ0可通过下式计算，

式中：γ—空气单位体积的重力（N）；g—重力加速度（m/s2）；v—风速（m/s）[9]。空气重度γ 的取值受当地的湿度、大气压和温度的影响，不同的纬度和海拔高度也会影响重力加速度g 的值均不相同，查表可知西安地区取γ2g。根据高空作业相关要求，在风力超过4 级时不得

进行外墙高空作业，即风速不得超过8m/s[9]，因此可得ω0=

0.044 kN/m2。将 βz=4.66，μs=0.96，μz=1.92，ω0=0.044kN/m2代入

式（1）中，可得西安地区 ϖk=0.3779kN/m2。

x 方向最大静风载，

Fxmax=ϖk·Sx投影=65N

y 方向最大静风载，

Fymax=ϖk·Sy投影=39N

z 方向最大静风载，

Fzmax=ϖk·Sz投影=21N

3.2 静态吸附状态机器人爬行机构安全吸附条件

静态吸附状态下机器人受力示意图，如图3 所示。此时，作用在玻璃幕墙清洗机器人上的力包括：重力G；负压吸附合力V（为两组吸盘的吸附力V1、V2之和）；驱动轮受到玻璃幕墙的支持力合力NW（为左驱动轮受到玻璃幕墙的支持力Nl和右驱动轮受到玻璃幕墙的支持力Nr之和）；吸盘受到玻璃幕墙的支持力合力Ns（为两组吸盘受到玻璃幕墙的支持力N1、N2之和）；驱动轮所受玻璃幕墙沿y 方向的摩擦阻力Ffly、Ffry；驱动轮所受玻璃幕墙沿z方向的摩擦阻力Fflz、Ffrz；吸盘所受玻璃幕墙沿y 方向的摩擦阻力Ff1y、Ff1y；吸盘所受玻璃幕墙沿z 方向的摩擦阻力Ff1z、Ff2z；驱动轮与玻璃幕墙的摩擦系数μWW，吸盘与玻璃幕墙的摩擦系数μSW；机器人在玻璃幕墙上所受静风载F，为机器人在x、y、z 方向的静风载Fx、Fy、Fz的合力。

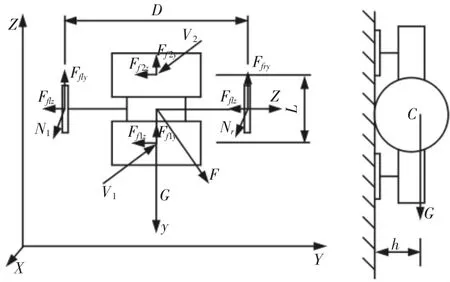
图3 静态吸附状态机器人受力示意图Fig.3 Force Diagram of the Robot in Static Adsorption State

由力平衡和力矩平衡可得支持力与摩擦力满足：

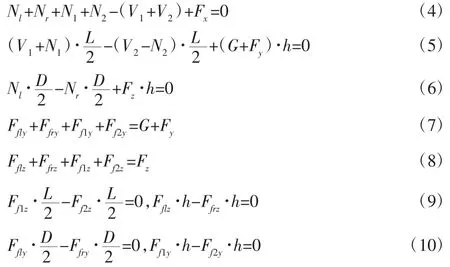
玻璃幕墙清洗机器人静态吸附在玻璃幕墙上时，两组吸盘和两个驱动轮所受的支持力共4 个，但与其相关的式子只有（4）～（6），故属于超静定求解问题。通过几何对称性并利用叠加原理求解这4 个支持力。

（1）在吸附力V 和静风载分力Fx单独作用下，各支持力均匀分布，分别为：

通过式（7）～式（10）可得各吸盘及驱动轮所受摩擦力分别为：

为使机器人在静止状态不发生滑移和倾覆，应满足以下条件：

将式（14）～式（19）带入不等式组（20）中，如果机器人在静态条件下不会发生滑移，那么也将不会发生倾覆。因此，吸盘吸附力V 需满足：

3.3 动态条件下机器人爬行机构的安全吸附条件

机器人在任意姿态下，以角速度ω（rad/s）做转弯运动时，设机器人本体加负载的总质量为M（kg），吸盘受玻璃幕墙的摩擦阻力矩为Ts（N.m），左驱动轮驱动力矩τl（N·m），右驱动轮驱动力矩τr（N·m），驱动轮半径r（m），机器人沿y 方向的加速度y¨产生的惯性力Fzy（N）和沿z 方向的加速度z¨产生的惯性力Faz（N）为：

动态条件下机器人爬行机构受力示意图，如图4 所示。

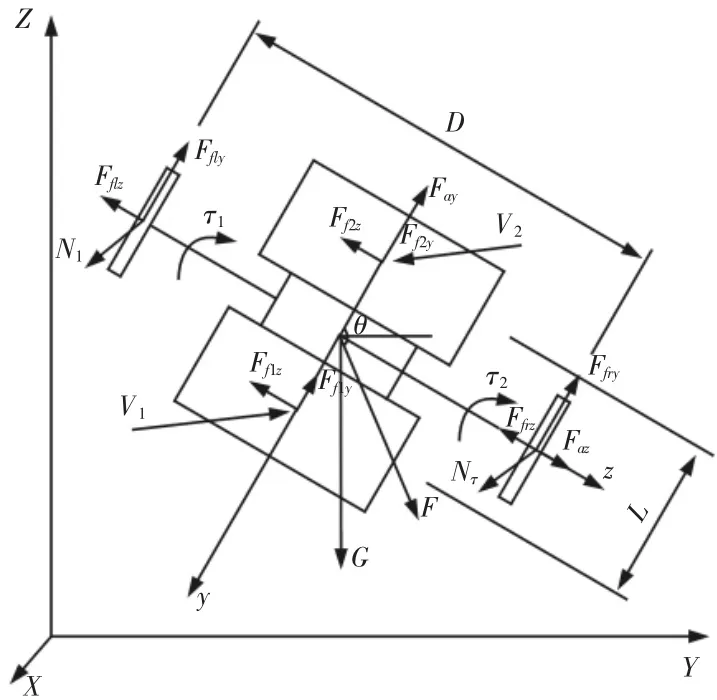
图4 动态条件下机器人受力示意图Fig.4 Force Diagram of the Robot Under Dynamic Conditions

由力平衡和力矩平衡可得机器人各支持力与摩擦力，分析计算可得动态条件下机器人吸盘吸附力V 需满足：

3.4 机器人爬行机构动力学分析

根据Newton-Euler 方程，机器人在玻璃幕墙上的任意运动都可简化为质心的平动和绕质心的转动，故可得机器人动力学方程组：

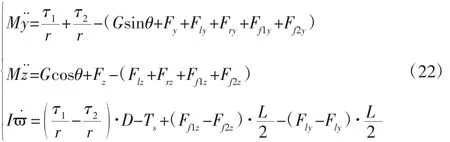
系统广义速度v˙=（y˙，z˙，θ˙）T与机器人沿y、z 方向的速度分量vy、vz关系如下：

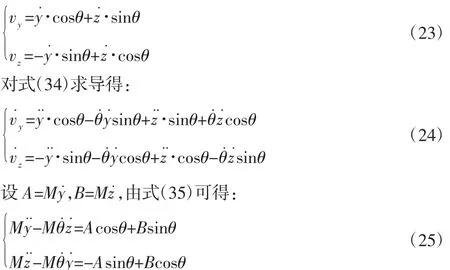
在机器人实际运动过程中速度较低，可取z¨=0，故将式（28）代入式（22）中可得：

4 机器人动力学仿真分析

4.1 机器人吸附力分析

本节模拟玻璃幕墙清洗机器人的实际运动状态，建立动力学模型，相关参数，如表1 所示。利用MATLAB 对机器人吸盘吸附力进行仿真分析。

表1 机器人参数Tab.1 Parameters of the Robot

由动态条件下机器人吸盘吸附力条件可得机器人在最大静风阻情况下机器人以0.05m/s2做匀加速运动工况时，吸附力随前进角的变化情况，如图5 所示，可以看出，机器人前进角在0～2π范围内变化过程中吸附力也随之周期变化，最大值为3830N，故须保证机器人吸附力大于3830N 以防止机器人在运动过程中发生滑移和倾覆。

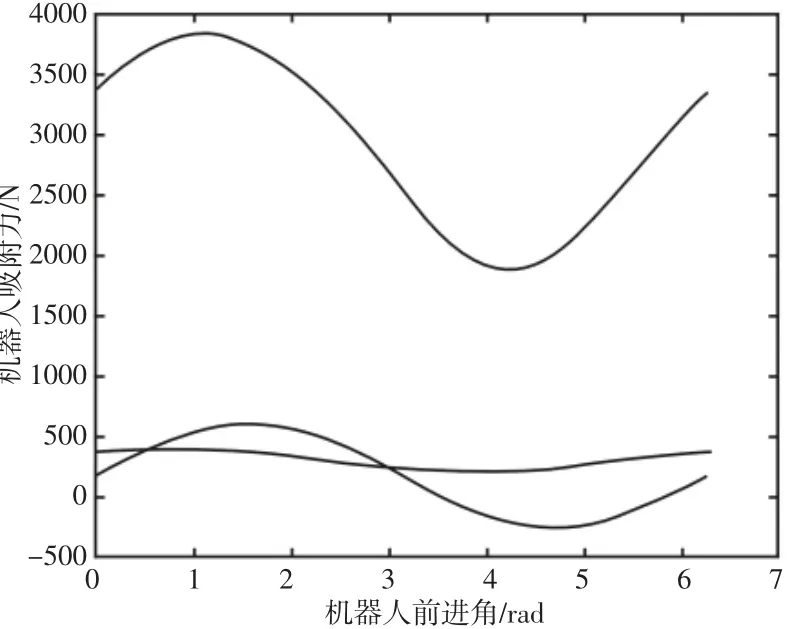
图5 动态条件下机器人吸附力示意图Fig.5 Adsorption Force Diagram of the Robot Under Dynamic Conditions

4.2 机器人驱动力矩分析

机器人在最大静风阻情况下以0.05m/s2做匀加速运动工况时吸附力为3830N 时驱动轮驱动力矩变化，如图6 所示。其中实线为左驱动轮驱动力，虚线为右驱动轮驱动力。机器人在运动过程中吸附力为3830N 时不同间距D 下左驱动轮驱动力矩示意图，如图7 所示，实线为D=1m 时，点划线为D=0.8m 时，虚线为D=0.6m 时，分析图中各曲线可知，D 越大，驱动轮驱动力越小，即驱动轮间间距越大机器人稳定性越高。

图6 动态条件下机器人驱动力矩示意图Fig.6 Driving Torque Diagram of the Robot Under Dynamic Conditions

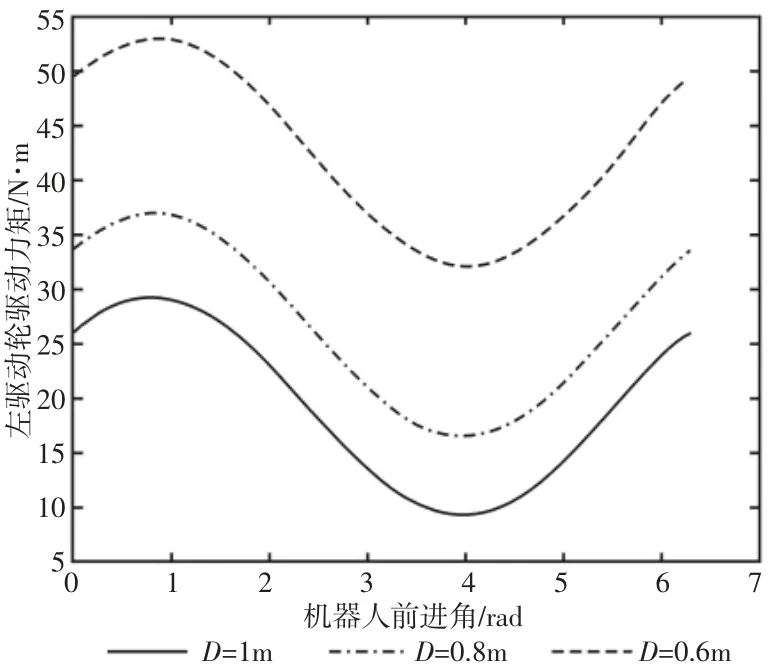
图7 不同间距D 下左驱动轮驱动力矩示意图Fig.7 Driving Torque Diagram of Left Drive Wheel in Different Spacing D

5 结论

设计了一种全新的玻璃幕墙清洗机器人爬行机构，并对机器人爬行机构动力学问题进行了分析。（1）分析了玻璃幕墙清洗机器人所受静风载情况，确定了机器人在西安地区实际工作中所受的最大静风载；（2）推导出了玻璃幕墙清洗机器人在静态吸附状态和动态条件下的安全吸附条件，并给出了机器人在实际工作中的最小吸附力；（3）通过计算玻璃幕墙清洗机器人的吸附力和驱动轮驱动力矩，从理论上确定了该爬行机构能使得机器人具有在平滑玻璃幕墙平稳移动的能力。