非线性边界条件下p-Laplacian脉冲边值问题的无界解序列
2020-10-21王立波
魏 颖,王立波
(1.北华大学计算机科学技术学院,吉林 吉林 132021;2.北华大学数学与统计学院,吉林 吉林 132013)
近年来,具p-Laplace算子或脉冲效应的非线性边值问题的多解存在性研究受到了诸多学者的广泛关注[1-9],其中多数要求方程右端非线性项在次线性及超线性之间具有某些扰动性.2010年,Wang L等[10]研究了一类具p-Laplace算子的 Sturm-Liouville脉冲边值问题在线性边界条件下无界解序列的存在性.
受上述文献启发,本文主要研究具p-Laplace算子的脉冲边值问题(BVP):
-(Φp(u′))′=f(t,u),t∈(0,1){t1,…,tm},
(1)
u′(0)=g0(u(0)),u′(1)=-g1(u(1)),
(2)
ΔΦp(u′(tk))=Ik(u(tk)),k∈{1,2,…,m}
(3)
无界解序列的存在性结果.其中:1 为方便起见,本文用(H) 表示如下条件: (H)函数f:[0,1]×→连续,函数g0、g1、Ik:→连续且单调不减,k=1,2,…,m. 定义泛函φ:W1,p(0,1)→为 (4) 其中:W1,p(0,1)为通常的Sobolev空间,范数配备为 定义1称函数α∈W1,p(0,1)为BVP(1)~(3)的下解,若 -(Φp(α′(t)))′≥f(t,α(t)),t∈(0,1){t1,…,tm}, α′(0)≥g0(α(0)),α′(1)≤-g1(α(1)). 称函数β∈W1,p(0,1)为BVP(1)~(3)的上解,若β满足上述相反的不等式. 定理1令α、β为BVP(1)~(3)的下、上解且满足α≤β,t∈[0,1].假设条件(H)成立,则由式(4)定义的泛函φ在[α,β]上能取到最小值,即存在满足α≤u≤β,t∈[0,1]的u∈W1,p(0,1)使得 进一步,u为BVP(1)~(3)的解. 证明:考虑修正问题 -(Φp(u′))′+φp(u)=φp(q(t,u))+f(t,q(t,u)),t∈(0,1){t1,…,tm}, (5) u′(0)=g0(u(0)),u′(1)=-g1(u(1)), (6) ΔΦp(u′(tk))=Ik(u(tk)),k∈{1,2,…,m}, (7) 其中q(t,u)=max{α(t),min{u,β(t)}}. 下面分2步证明. 对任意的v∈W1,p(0,1),有 从而u满足 (Φp(u′))′-φp(u)+φp(q(t,u))+f(t,q(t,u))=0,t∈(tk,tk+1), 即u满足式(5). 即ΔΦp(u′(tk))=Ik(u(tk)),∀k∈{1,2,…,m}. 对式(5)在(0,1)上应用分部积分,由u满足式(5)及式(7),可得 [-Φp(u′(0))+Φp(g0(u(0)))]v(0)+[Φp(u′(1))+Φp(g1(u(1)))]v(1)=0. 下证u满足式(6).不失一般性,假设u′(0)-g0(u(0))>0.令v(t)=1-t∈C,可得以下矛盾: 0=-Φp(u′(0))+Φp(g0(u(0)))>0, 从而u′(0)=g0(u(0)).类似可得u′(1)=-g1(u(1)),从而u为问题(5)~(7)的解. 第2步.u为BVP(1)~(3)的解. 只需证明α≤u≤β,t∈[0,1]. [Φp(u′(1))-Φp(β′(1))](u(1)-β(1))+-[Φp(u′(0))-Φp(β′(0))](u(0)-β(0))+- 由Φp的单调性,有 若u(0)-β(0)≤0,有 [Φp(u′(0))-Φp(β′(0))](u(0)-β(0))+=0. 若u(0)-β(0)>0,由上下解的定义及函数g0的单调性可得 u′(0)-β′(0)≥g0(u(0))-g0(β(0))≥0. 从而Φp(u′(0))-Φp(β′(0))>0且-[Φp(u′(0))-Φp(β′(0))](u(0)-β(0))+≤0. 类似可得[Φp(u′(1))-Φp(β′(1))](u(1)-β(1))+≤0.从而 即u(t)≤β(t),t∈[0,1].类似可得u(t)≥α(t),t∈[0,1],从而u为BVP(1)~(3)的解. 定理2设函数f:[0,1]×→连续.假设 (A2)在[0,1]上一致地有 - (A3)ug0(u)≥0,∀u∈且 则BVP(1)~(3)有两个解序列{un}及{vn},满足 …≤vn+1≤vn≤…≤v1≤u1≤…≤un≤un+1≤… 及 证明:下面分5步证明. 第1步.对任意的M≥0,BVP(1)~(3)存在上解β,使得β≥M,t∈[0,1]. 由(A1),存在K≥0使得在[0,1]×[0,+)上有 f(t,u)+K≥0 (8) 及 F(t,u)+Ku≥0. (9) 对任意给定的M>0,选取充分小的正数ε.由(A3),存在d>0,使得 (10) 定义β为初值问题 (Φp(u′))′+f(t,u)+K=0,u(0)=d,u′(0)=0 F(t,β(t))+Kβ(t)≥0,t∈[0,t0]. 由式(10),有 即0≤-β′(t)≤εd.则对任意的t∈[0,t0],d-β(t)≤εdt0≤εd,得如下矛盾: β′(0)-g0(β(0))≤0 及 第2步.对任意的M≥0,BVP(1)~(3)存在下解α,使得α≤-M,t∈[0,1]. 由(A1),存在L≥0使得在[0,1]×(-,0]上有 f(t,u)-L≤0 (11) 及 F(t,u)-Lu≥0. (12) 对任意给定的M>0,选取充分小的正数δ.由(A3),存在d>0,有 (13) 定义α为初值问题 (Φp(u′))′+f(t,u)-L=0,u(0)=-d,u′(0)=0 即0≤α′(t)≤δd,从而对任意的t∈[0,t0],α(t)+d≤δdt0≤δd,得矛盾: α′(0)-g0(α(0))≥0 且 第3步.存在满足sn→+的正数序列{sn}使得φ(sn)→-. 由(A2),存在正数序列{sn},使得sn→+且 则有 第4步.存在满足tn→-的负数序列{tn}使得φ(tn)→-. 由(A2),存在负数序列{tn},使得tn→-且 则有 第5步.由第1步及第2步,BVP(1)~(3)存在下、上解α1、β1使得α1≤β1,从而由定理1,BVP(1)~(3)存在解u1,使得α1≤u1≤β1. 由第3步,存在s1使得s1>u1且φ(s1)<φ(u1).进一步,由第1步,存在上解β2使得u1≤s1≤β2.由定理1,BVP(1)~(3)存在解u2使得u1≤u2≤β2,且 从而u1≠u2. 继续下去,可得 un≤un+1≤βn+1,φ(un+1)≤φ(sn)<φ(un),n=1,2,…, 由φ(sn)→-,有φ(un)→-,即 类似可证BVP(1)~(3)存在解序列{vn},使得 证毕. 例1考虑p-Laplacian脉冲边值问题 -(Φp(u′))′=f(t,u),t∈(0,1){t1,…,tm}, (14) u′(0)=g0(u(0)),u′(1)=-g1(u(1)), (15) ΔΦp(u′(tk))=Ik(u(tk)),k∈{1,2,…,m}, (16) 其中p=5.函数f:→定义为 其中λ=ee,函数g0、g1、Ik:→定义为 则易见 及 ug0(u)≥0, ∀u∈, 则由定理2,边值问题(14)~(16)有两个解序列{un}及{vn},满足 …≤vn+1≤vn≤…≤v1≤u1≤…≤un≤un+1≤…1 主要结果
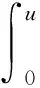


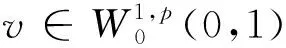
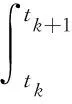



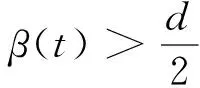
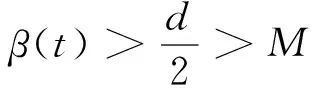


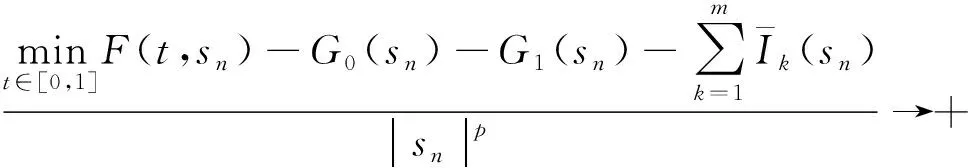

2 数值算例
