基于双字典的噪声环境下的语音转换方法
2020-10-21简志华胡伟通汪云路
周 迪,简志华,胡伟通,汪云路
1(浙江宇视科技有限公司,杭州 310051) 2(杭州电子科技大学 通信工程学院,杭州 310018) 3(杭州电子科技大学 网络空间安全学院,杭州 310018)
1 引 言
语音转换是一种改变语音信号中说话人特性的技术,它将一个人的声音变成另外一个人的声音,而不改变其中的语义内容[1,2].
高斯混合模型(Gaussion Mixture Model,GMM)作为一种概率统计模型,常用于语音转换,是一种主流的转换方法,它的转换函数是一种加权求均值的形式[3-6].这种转换方法易于实现且效果不错,但存在两点不足:一是统计平均的转换函数会使得转换后的语音谱包络过于平滑,降低语音自然度;二是为了减少模型训练时的计算量,特征参数常常是低维的,如MFCC、LSP等,但低维参数会损失语音中较多的信息,会使音质下降.最近几年,稀疏字典在语音处理的多个领域都得到了很好的应用,基于语音样本字典的转换算法逐渐发展了起来.这些算法常采用高维的语音谱作为特征参数,并用非负矩阵分解(Non-negative Matrix Factorization,NMF)求解转换函数[7-10].该类算法有效地改进了基于统计参数方法的频谱过于平滑以及由于语料不足所造成的过拟合问题,产生更加自然的语音.但是,上述语音转换算法在实际的噪声应用环境下,由于噪声的存在,使得实验室纯净语音训练的转换系统的性能激剧下降,无法满足很多实际场景的应用需求.
论文在以往NMF转换方法基础上,提出了采用两个字典联合起来实现噪声环境下的语音转换.该算法在训练阶段,通过语音库中的纯净语音得到源语音字典和背景噪声字典,并将两者相结合;在语音转换时,用联合字典将输入的带噪语音进行稀疏表示,根据源语音字典的权值矩阵和目标语音字典就可以得到转换后的语音,从而完成含噪语音的转换.
2 基于NMF的语音转换
稀疏表示是NMF语音转换的核心[8],假定某说话人的特征矢量x∈RL×1,则可由其基矢量序列表示为:
(1)
其中J是基矢量aj总的数目,所有这些基矢量就构成语音字典A=[a1,a2,…,aJ],而hj是相应基矢量的加权系数,并形成权值矢量h=[h1,h2,…,hJ]T.
假定有一段D帧的语音,用X∈RL×D表示它的特征矢量序列.利用公式(1),X可表示为:
X=AH
(2)
其中H∈RJ×D表示权值矩阵.
为实现转换,在训练阶段,对源和目标说话人的特征矢量序列用动态时间规整(Dynamic Time Warping,DTW)进行对齐[11],并建立平行的源语音字典A和目标语音字典B.因此,转换函数可以表示为:

(3)

3 噪声鲁棒性的语音转换
在NMF转换算法中,由目标语音字典B和源语音的权值矩阵H就可以实现语音转换,但如果在有噪的环境下,即待转换的语音是含有噪声的,由纯净语音训练得到模型与含噪语音之间存在不匹配,因此语音转换系统性能会下降,不能有效地实现转换.为此,论文采用增加噪声字典的方式提出了一种噪声鲁棒性的NMF语音转换算法(Noise Robust NMF,NR-NMF).
3.1 联合字典的生成
联合字典包含了语音字典和噪声字典,字典中的原子是一帧信号的频谱,由于转换阶段的输入语音是含噪的,语音信号的频谱通过短时傅里叶变换(Short Time Fourier Transform,STFT)来计算.但在训练阶段,由于源语音和目标语音都是纯净语音,对它们进行动态时间规整过程中,采用由STRAIGHT模型[12]导出的MCC (Mel-Cepstral Coefficients)作为特征参数来进行规整,再根据这些规整信息来获得对齐的源、目标语音STFT频谱参数序列,并建立平行的源语音、目标语音字典As和Bs.
同时引入噪声字典An,将语音字典As与噪声字典An一同构成联合字典A,即:
A=[AsAn]
(4)
为使噪声字典An与实际应用场景相匹配,论文提取实际环境下的噪声STFT频谱作为噪声字典.联合字典A生成过程示意图如图1所示.
3.2 权值矩阵的估计
假设含噪语音中任意第d帧的STFT频谱特征参数为xd,则有:
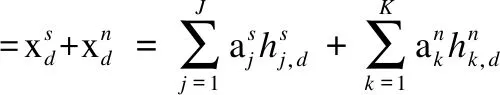
=Ahds.t. hd≥0
(5)

图1 生成联合字典的流程图Fig.1 Flow chart for generating the joint dictionary
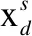
=AHs.t.H≥0
(6)
在X和A已知的情况下,通过最小化损失函数来估计权值矩阵H,即:
H=arg min{dKL(X,AH)+‖λΛ1×D.*H‖1}s.t.H≥0
(7)
式(7)中,dKL(·)是KL散度,λ=[λ1…λJ…λJ+K]T是稀疏惩罚因子,包含语音部分惩罚因子和噪声部分惩罚因子,‖·‖1是l1范数.权值矩阵H可由乘性迭代更新规则得到[8],即:
(8)
其中⊗表示点乘,式中除法都是点除,矩阵ΛL×D,Λ1×D中的元素都是1.
3.3 特征参数的转换
权值矩阵H包含了语音字典的权值矩阵Hs和噪声字典的权值矩阵Hn,即:
(9)
因此转换后的目标语音频谱为:
(10)
3.4 基音频率的转换
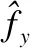
(11)
本文所提出的语音转换系统原理框图如图2所示.

图2 语音转换系统原理框图Fig.2 Framework of voice conversion system
4 实验及结果
实验采用的CASIA语音库是实验室安静环境下的汉语语音.语音库采用相同的文本,即每个人的发音内容是一样.信号的采样频率为16KHz,采用16位比特量化.实验随机选用150句作为训练集,50句作为测试集.采用1024点的FFT计算语音STFT频谱,语音帧长为20ms,帧移为10ms.而含噪语音由噪声库Noisex-92中的5种常见噪声(white、pink、babble、factory、volvo)叠加纯净语音得到.
论文采用文献[8]中的差异值作为两个矢量序列之间距离度量,表示为:
(12)
差异值E越小,两个矢量序列之间就更具有相似性.
4.1 实验参数的选择
实验中联合字典包括语音字典部分和噪声字典部分,通过使用该联合字典达到含噪语音与字典的匹配.论文先进行了两个字典大小选择的实验,其中NMF循环迭代次数预选择为400,稀疏惩罚因子λ为0.1.图3显示了含噪语音和经过NMF分解重构后语音之间的差异值E跟两个字典大小关系.
由图3(a)可以看出,在不同噪声字典大小情况下,随着语音字典帧数J增大,含噪语音及其重构语音之间的差异值E逐渐减小,并且字典帧数J达到4000以后,差异值E逐渐趋于稳定,因此语音字典帧数选择为4000帧.从图3(b)来看,在各种语音字典大小J的条件下,随着噪声字典大小K的增大,含噪语音及其重构语音之间的差异值E均逐渐减小,但减小量的越来越小.由于转换算法在实际的应用中,需要从背景环境中获取噪声,噪声字典过大,则需要提取较长时间,不适合实时的处理,所以折中考虑选择噪声字典大小K为2000帧.

图3 差异值E和语音字典大小、噪声字典大小的关系Fig.3 Relationship between distortion E and the size of speech dictionary,noise dictionary
在求取H的循环迭代计算中,将噪声字典所对应的稀疏惩罚因子都设置为0,这是因为噪声不具有稀疏性.因此,本文实验只研究语音字典的稀疏惩罚因子对转换性能的影响,并将稀疏惩罚因子λ设置在0.1-0.9的区间,而循环迭代次数从0到400变化,含噪语音及其经NMF分解重构语音之间的差异值E的变化曲线如图4所示.

图4 差异值E和惩罚因子λ、迭代次数Fig.4 Curves of distortion E and number of iterations under different penalty factor λ
由图4来看,迭代次数达到200次以后各条曲线的值几乎不会随循环次数的增加而有所变化,因此论文将循环迭代次数设定为200.同时,随着λ的值从0.9减小到0.1,重构前后语音特征矢量之间的差异值E逐渐减小.为进一步确定参数λ的取值,本文比较了λ从0.1减小到0.01时,用图2所示的转换系统对含噪语音进行转换,转换后的语音频谱与对应的目标语音频谱之间的差异值E如图5所示.

图5 转换系统差异值E和惩罚因子λ之间的关系Fig.5 Curve of distortion E and penalty factor λ after conversion
由图5可以看出,稀疏惩罚因子λ为0.04时,转换频谱与目标频谱差异值E达到最小,因此语音字典的权值矩阵所对应的惩罚因子为0.04.
4.2 转换性能测试
我们将传统的NMF转换算法[8]与本文NR-NMF算法进行性能对比,同时为了增强NMF算法抗噪能力,在转换之前采用谱减法进行降噪处理[14,15],将该方法称为SS-NMF(Spectral Subtraction NMF)算法.图6是NMF、SS-NMF以及NR-NMF 3种算法的差异值对照图.

图6 3种转换算法的性能比较Fig.6 Performance comparison of the threeconversion algorithms
图6中的差异值E是表示含噪语音进行转换后的语音频谱与对应的目标语音频谱之间的差异值.从图中可以看出,随着SNR由-5dB逐渐增大到20dB时,转换语音与目标语音的差异值E逐渐减小,说明当输入语音不管是含噪语音还是较为纯静的语音,本算法都具有较好的转换效果.由图中NMF曲线与NR-NMF曲线的比较可以看出,在各种信噪比条件下NR-NMF算法的差异值都比传统的NMF算法要小,而且信噪比越低,NR-NMF算法的性能优势更明显.同时,与SS-NMF算法相比,在高信噪比时,两者的差异值接近,但在低信噪比时,NR-NMF算法的差异值明显要小,说明本文算法虽然在高信噪比时与SS-NMF算法的性能相当,但在低信噪比时对转换系统的性能有很大的提升.图7显示的是语音受白噪声干扰,信噪比为0dB的情况下,分别用NR-NMF与SS-NMF转换后语音的语谱图对比.图7(a)为待转换的含噪语音语谱图,图7(b)为目标语音语谱图,图7(c)为SS-NMF转换后的语谱图,图7(d)为NR-NMF转换后的语谱图.由图7(b)、图7(c)比较可以看出SS-NMF算法在SNR=0dB低信噪比下存在较多的噪声残留,因此转换效果明显变差,由图7(b)、图7(d)比较可以看出NR-NMF算法转换后的语谱图存在极少的噪声残留,转换效果优于SS-NMF.

图7 白噪声环境下(SNR=0dB)NR-NMF与SS-NMF的对比Fig.7 Comparison of NR-NMF and SS-NMF with white noise when SNR=0dB
为比较本文算法在其他不同噪声的情况下也具有较好的性能,论文分别在pink、babble、factory、volvo这4种噪声的情况下进行了实验,实验结果见表1所示.从表1来看,NR-NMF算法分别在6种不同的信噪比情况下都比传统的NMF算法具有更小的差异值,特别在低信噪比时具有更好的性能优势.

表1 NR-NMF与NMF在不同噪声情况下的差异值对比Table 1 Comparison of distortion for NR-NMF and NMF with different noises
综上实验表明,NR-NMF算法具有非常好的噪声鲁棒性,在低信噪比情况下也能实现较好的转换效果,同时该算法在多种噪声环境下也都有更好的转换性能.

表2 NMF、SS-NMF与NR-NMF的MOS分对照Table 2 Comparison of MOS of NMF, SS-NMF and NR-NMF
语音转换系统性能的测试,不仅包括客观评测,还包括主观评价.论文对转换系统的性能进行了主观评价,采用的方法是MOS打分,它是用来评价转换后的语音质量.MOS打分的评测结果如表2所示.从表2中的实验结果来看,本文算法NR-NMF比SS-NMF和NMF算法都具有更高的MOS分,同时,由于引入了降噪功能,SS-NMF转换后的语音比NMF具有更好语音质量.
5 结 论
论文通过引入噪声字典,提出了一种具有噪声鲁棒性的语音转换算法NR-NMF.将噪声字典与源语音字典进行联合,以匹配各种不同噪声环境下的语音,实现在噪声环境下的语音转换.实验结果表明,该算法在噪声环境较为恶劣的情况下也能很好地实现语音转换.同时,该算法中噪声数据可以直接由说话人所处环境中采集得到且无需在前端增加额外的消噪模块,所以极大的方便了语音转换的应用.
