昌吉市MODIS气溶胶光学厚度与AQI的关系模型研究

周琪　苗运玲　林琳　柴岩红

摘要：为了建立昌吉市近地面AQI监测的关系模型，利用昌吉市2015—2016年MODIS AOD产品与同期地面观测的AQI进行相关分析，结果表明二者直接相关程度较低（R2=0.2921，p<0.01）;按照季节分类统计（春、夏、秋）的相关系数R2分别为0.4629、0.4192、0.3487，均大于统计学上99%的置信度要求;加入气象因子风速，建立含气象因子的AQI和AOD的多元回归模型，结果表明全年及各季的相关系数R2分别为0.3648、0.4528、0.4247、0.5089;对气象因子风速进行分级，在综合考虑R2检验值和F检验值的基础上，平均风速>2m·s-1时的模型为线性模型R2为0.47，预测平均相对误差为10.8%，结果较好。文章为监测空气污染提供了一定的参考价值。

关键词：气溶胶光学厚度（AOD）;空气质量指数AQI;PM2.5;拟合模型

中图分类号：S-3

文献标识码：A

作者简介：周琪（1988-），女，硕士，工程师。研究方向：卫星遥感与环境气象应用。

随着我国经济的快速增长，大气污染问题日益严重[1，2]。可吸入颗粒PM2.5（空气动力学直径小于或等于2.5μm的粒子）已成为影响环境空气质量的首要污染物[3]，影响人类正常的生产生活。目前监测PM2.5的站点分布不均匀且数量有限，缺乏空间上的连续监测[5]。大气气溶胶的光学厚度AOD可以在一定程度上反应区域大气的污染程度[4]。卫星遥感具有获取信息快、覆盖面积广的特点，在污染监测上有广泛应用前景[2，6]。Chu D A etal[7]展示了MODIS产品在监测全球、区域和局部空气污染状况方面的能力，表明可以用MODIS AOD产品进行大气污染监测。焦利民等[8]以京津冀为研究区，研究AOD与PM2.5浓度相关关系的空间差异和时间变化。黄观等[9]利用多分辨率的MODIS气溶胶产品，得出北疆区域近14a平均AOD大体呈现中心高、边缘低的分布格局。范辰乾[10]进行了济南市基于MODIS数据的气溶胶光学厚度与PM2.5浓度的关系研究，得出MODIS数据反演气溶胶光学厚度对建立PM2.5观测和预测体系具有一定的科学性和可行性的结论。

近年来随着昌吉市经济的迅速发展，伴随着严重的环境问题。目前对昌吉地区MODIS气溶胶光学厚度AOD与空气质量指数AQI的相关研究较少。本文利用MODIS数据和空气污染监测数据，建立空气质量指数AQI与AOD之间的关系模型，并分季节建立最佳模型，同时考虑加入气象因子进行分析，以实现利用遥感技术监测地面空气污染状况，为监测空气污染提供一定的参考价值。

1研究区概况与数据方法

1.1数据来源与处理

1.1.1气溶胶光学厚度AOD

本文采用的是美国宇航局（NASA）的地球观测系统（EOS）卫星Aqua的中分辨率成像光谱仪（MODIS）的气溶胶Level2光学厚度产品AOD，由暗像元业务算法生成，分辨率为10km，用灰度值来表示光学厚度的大小。

1.1.2空气质量指数AQI

研究所用的AQI数据，采用昌吉市环境监测站获得的监测数据，每日提供2个站点的数据信息，站点的相关信息如表1所示。

1.2数据匹配

研究中涉及到的变量有MODIS AOD、近地面PM2.5浓度、空气质量指数AQI。数据匹配原则是空间上以2个监测站点为准，时间上以卫星过境时间为准，选取数据对中晴无云天气，剔除有降水天气的数据。经匹配处理后共得到2015—2016年的数据86对。冬季卫星遙感产品在“亮背景”下反演效果较差，基本无有效数据，考虑到这点没有进行冬季的建模与检验。将AQI按照升序排列后，每隔3个样本选取1个样本作为模型验证数据，得到建模数据58对，验证数据28对。

1.3方法与思路

主导气象因子分析，选取气压、气温、相对湿度、风速和日照5个气象因子，进行AQI、AOD与5个气象因子的相关分析，选取主导气象因子，并将主导气象因子进行分组。

直接相关，直接进行全年及各季节卫星遥感AOD和近地面AQI之间的相关性分析，并进行模型对比。

加入主导气象因子参与的全年及各季节AOD与AQI之间的多元回归模型，将主导气象因子进行分级，分别建立相应的回归模型;将之前建立的所有最佳模型的拟合精度和预测精度进行对比分析。

2结果与分析

2.1主导气象因子分析

2.1.1主导气象因子的选取

本课题研究的空气质量指数AQI与AOD关系时考虑的是每日平均状况，因此只讨论气压、气温、相对湿度、风速和日照5个气象因子。AQI、AOD与5个气象因子的相关系数见表2，从表2中可以看出AQI、AOD与平均风速均成正相关，且相关性较其它4个因子的相关性显著。因为风速对空气污染物的扩散和传输起主导作用，当风速达到一定量时，会有助于空气污染物的扩散和传输，而当风速较小时，则不利于空气污染物的扩散和传输，会在一地形成堆积。因此选取平均风速为主导气象因子。

2.1.2气象因子分级

当风速≤2m·s-1时，风力较为微弱，不利于空气污染细颗粒物扩散，容易造成堆积;当风速>2m·s-1时，空气污染细颗粒物质被风驱散，污染状况得到改善。因此，以风速2m·s-1为界分级，将86d数据按照平均风速大小进行排序分成2个部分，即平均风速≤2m·s-1共33个样本和平均风速>2m·s-1共53个样本。

2.2AOD与AQI的直接关系模型分析

2.2.1全年AQI与AOD关系模型

将86d数据按照AQI值得大小进行重新排序，根据AQI值从低到高每隔2个样本选取1个样本作为检验模型所用。这样原始数据分为2部分，一部分用来建模，共58个;一部分用来验证模型，共28个。

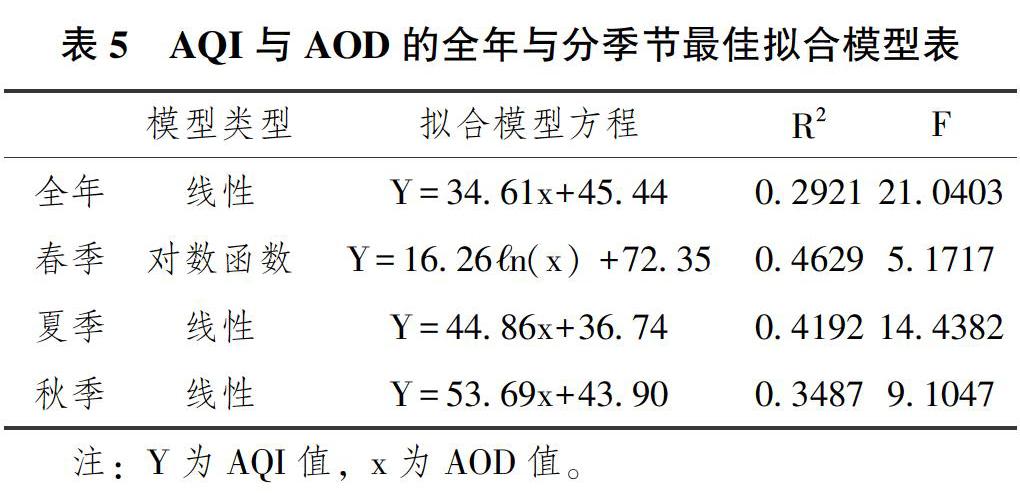
将建模样本中的AOD值作为自变量，AQI作为因变量，进行回归分析，模型类型包括指数函数、对数函数、幂函数、线性和一元二次方程，分析结果见表3。从表3中可以看出，几个模型中，幂函数好于对数函数，指数函数好于幂函数，如果仅考虑R2检验值，则一元二次模型好于线性模型，但再从F检验值分析，Y=34.61x+45.44应为最佳选择，如图1所示。

2.2.2分季节AQI与AOD关系模型

通过分季节来研究AOD与AQI之间的关系，将58个建模样本数据和28个检验样本数据按照季节分类。本研究的季节划分按照3—5月为春季、6—8月为夏季、9—11月为秋季、12月—次年2月为冬季来划分。对于不同的季节分别进行模型分析，在指数函数、对数函数、幂函数、线性和一元二次方程5种模型中，综合考虑R2检验值和F检验值的基础上，相应地选择各季节最佳模型，分析结果见表4。春季对数函数为最佳模型，夏季和秋季线性模型为最佳选择。3个季节相应的散点图和拟合模型如图2。

从表5中可以看出，全年建模样本和季节建模样本建立的拟合精度较高的4个模型中，夏季线性模型，AQI与AOD相关系数最高，秋季次之。

通过利用各自建模样本数据对模型进行误差分析，全年样本线性模型的平均相对误差为15.56%，春季对数函数模型的平均相对误差为7.57%，夏季線性模型的平均相对误差为19.45%，秋季线性模型的平均相对误差为14.61%。

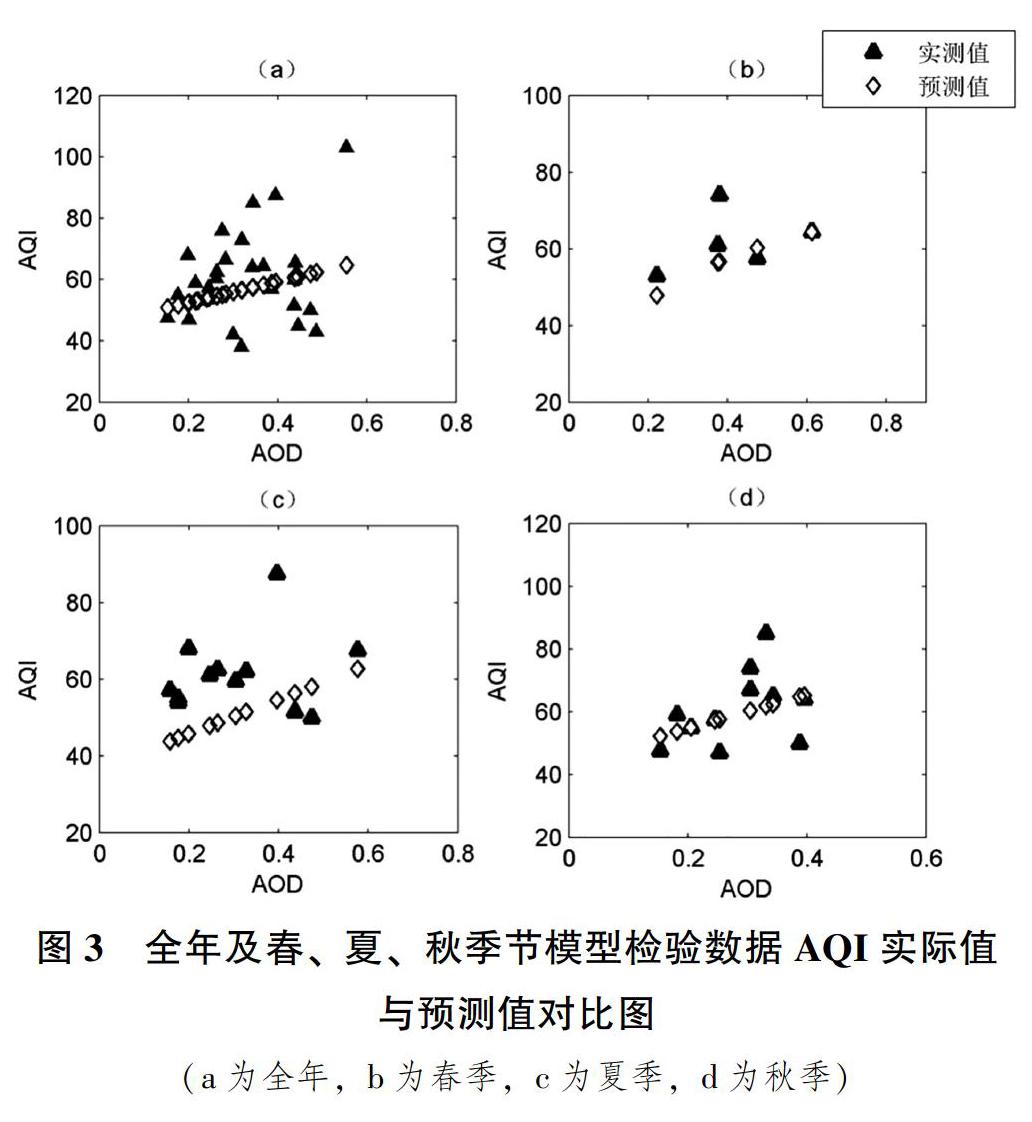
进一步利用各自检验样本数据对模型进行预测评价，全年样本线性模型的平均相对误差为18.77%，春季对数函数模型的平均相对误差为10.89%，夏季线性模型的平均相对误差为25.76%，秋季线性模型的平均相对误差为12.59%。将相应的检验样本数据带入各模型，估算出的AQI值与实际值进行分析可以看出，全年、夏季模型预测值和实际值吻合度很低（见图3），春季除1个点外，其余点的预测值和实际值可以达到较好逼近，秋季各点预测值和实际值逼近效果也较好。由此可见，春季AQI与AOD之间存在简单的对数函数关系，秋季AQI与AOD之间存在简单的线性关系。

2.3含气象因子的AQI与AOD多元关系模型

2.3.1含气象因子的全年及各季节AQI与AOD关系模型

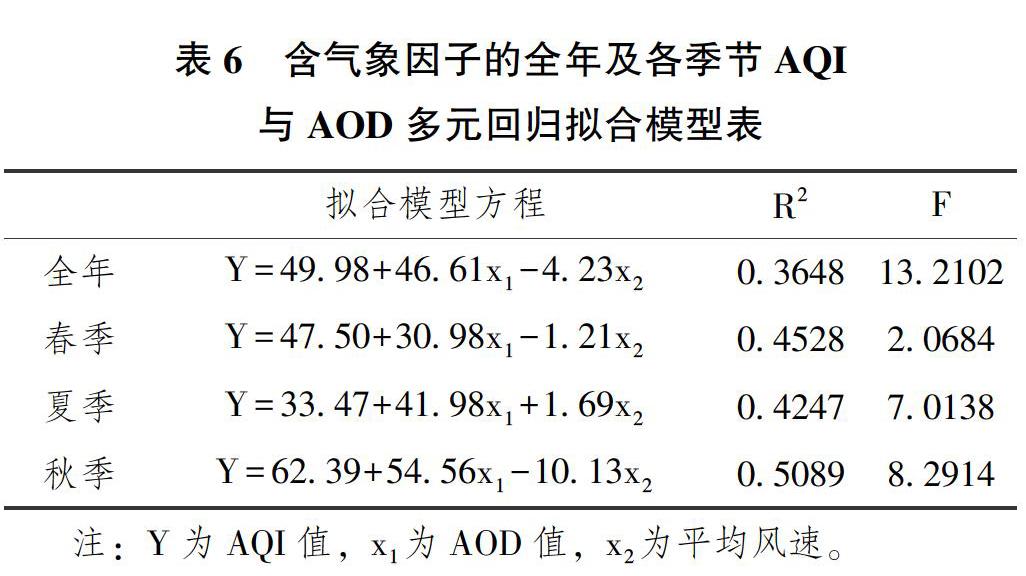
将建模样本中AOD值、平均风速作为自变量，AQI值作为因变量，进行多元回归分析，分析结果见表6。

2.3.2气象因子分级的关系模型

通过前面选定的主导气象因子平均风速对58个样本数据和28个检验数据进行分级，将数据重新分类到2个类别中，依次是平均风速≤2m·s-1和平均风速>2m·s-1，然后建立相应的回归模型，分析结果见表7。

综合考虑R2检验值和F检验值的基础上，平均风速≤2m·s-1时的最佳模型为指数函数，平均风速>2m·s-1时的最佳模型，为线性模型。

2.3.3气象因子分级模型的对比分析

利用各自建模样本数据对模型进行误差分析，平均风速≤2m·s-1时的平均相对误差为15.76%，平均风速>2m·s-1时的平均相对误差为16.01%。进一步利用各自检验样本数据对模型进行预测评价，平均风速≤2m·s-1时的平均相对误差为13.14%，平均风速>2m·s-1时的平均相对误差为10.8%。将相应的检验样本数据带入各模型，估算出的AQI值与实际值进行分析可以看出，2组模型预测值和实际值吻合度较低（见图4），只有个别点的预测值和实际值可以达到较好逼近。

2.4所有模型对比分析

将之前建立的所有最佳模型的拟合精度和预测精度进行对比分析，结果见表8。综合考虑R2、F值、拟合平均相对误差和预测平均相对误差，可以看出季节模型里春季模型有较好的实用价值，而当有气象因子参与建模时，除春季外各模型的相关系数普遍提高，模型质量有所提高。

在使用气象因子分组讨论AOD与AQI相关性时，平均风速>2m·s-1时，模型相关系数R2为0.47，比平均风速≤2m·s-1时的拟合程度要好。

3讨论

虽然MODIS气溶胶光学厚度和AQI指数的相关分析，从一定程度上可以反映地面污染状况。但由于MODIS卫星数据只有在晴好天气才能获得数据，如果遇上阴雨天气，则不能利用AOD监测空气污染情况，对本研究有一定限制;冬季在“亮背景”下反演效果差，基本无数据，因此本文中没有冬季相关内容的研究。

本文考虑的气象因子只有平均风速，而且没有分季节讨论不同的气象因子的作用，虽然污染监测的准确度有了一定提高，但没有达到最理想的效果。在今后的研究中有必要考虑更多的气象因子，并且着重考虑不同季节不同气象因子的作用，应该会得到更好的结果。

4结论

全年和季节空气质量指数和气溶胶光学厚度建立回归模型，比较各模型精度，得出春季对数函数模型和夏季线性模型较为理想，春季相关系数为0.4629，夏季相关系数为0.4192。

讨论常规的气象观测数据，选取主导气象因子为风速，对全年和季节模型进行重建，发现有主导气象因子参与的多元回归模型相关系数普遍比没有气象因子参与的一元回归模型高。

依据主导气象因子风速将样本数据分组，各组空气质量指数和气溶胶光学厚度建立回归模型，讨论其精度，发现当平均风速>2m/s时，模型相关系数R2为0.47，预测平均相对误差为10.8%，结果较好。

参考文献

[1]张晖，王伯铎，陈良富，等.西安市及周边地区MODIS气溶胶光学厚度与PM10浓度关系模型研究[J].环境工程学报，2014，8（02）：665-671.

[2]黃观，刘伟，刘志红，等.乌鲁木齐市MODIS气溶胶光学厚度与PM10浓度关系模型研究[J].环境科学学报，2016，36（02）：649-657.

[3]陈飞龙，王召海，王其新.济南市MODIS气溶胶光学厚度和PM2.5浓度的特征及相关性分析[J].鲁东大学学报（自然科学版），2016，32（01）：86-91.

[4]刘勇.MODIS气溶胶光学厚度与南京主城区空气污染指数的关系研究[D].南京：南京师范大学，2007.

[5]王贺锐，吴彩保.MODIS气溶胶产品在北京监测PM2.5质量浓度中的应用[J].环境科学，2016，13（20）：76-78.

[6]李成才，毛节泰，刘启汉.利用MODIS资料遥感香港地区高分辨率气溶胶光学厚度[J].大气科学，2005，29（03）：335-342.

[7]Chu D A ， Kaufman Y J ， Zibordi G ， et al. Global monitoring of air pollution over land from the Earth Observing System-Terra Moderate Resolution Imaging Spectroradiometer （MODIS）[J]. Journal of Geophysical Research Atmospheres， 2003，108（D21）：466-467.

[8]焦利民，张博恩，许刚，等.气溶胶光学厚度与PM2.5浓度相关关系的时空变异[J].干旱区资源与环境，2016，30（12）：34-39.

[9]黄观，刘志红，刘伟，等. 北疆地区气溶胶光学厚度的时空特征[J]. 生态与农村环境学报，2015，31（03）：286-292.

[10]范辰乾. 基于MODIS数据的气溶胶光学厚度与PM2.5浓度关系研究——以济南市为例[D].济南：山东师范大学，2015.

（责任编辑 李媛媛）