蒙特卡洛与马尔可夫方法在降水预测中的应用

黄鹤 张维江 李娟

摘 要：为了更深入地分析原州区的降水特征，为该区域水资源预测提供依据，基于原州区1957—2016年60 a降水资料，采用蒙特卡洛方法推求降水分布，采用K-S检验对模型进行显著性检验，采用基于欧氏距离的层次聚类方法进行状态划分，确定了原州区的降水分布，建立了适用于原州区的滑动平均加权马尔可夫预测模型。根据已有数据验证了预测结果的有效性，再结合已确定的降水分布，通过K-S检验，检验了未来5 a降水预测的准确性。结果表明：原州区降水分布符合P-Ⅲ型分布;马尔可夫模型适用于原州区降水预测，且未来5 a的降水预测结果是准确的，分别为508.5、520.8、554.9、451.0、466.6 mm。

关键词：蒙特卡洛方法;马尔可夫模型;随机模拟;降水预测;原州区;K-S检验

中图分类号：TV11 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.05.004

Abstract： In order to analyze the characteristics of precipitation in YuanzhouDistrict and provide a basis for water resources prediction in the region， based on the precipitation data from 1957 to 2016 of the district， the Monte Carlo method was used to estimate the precipitation distribution and the K-S test was used to model the significant test. It used the hierarchical clustering method based on Euclidean distance to divide the state， determined the precipitation distribution of the region and established a sliding average weighted Markov prediction model which was suitable for Yuanzhou District. Based on the existing data， the true validity of the prediction results was verified. Combined with the determined precipitation distribution， the accuracy of precipitation prediction for the next 5 years was tested by K-S test. Comparing with Pearson three-type distribution， the results show that the precipitation distribution in Yuanzhou District is more consistent with the log-normal distribution. The Markov model can be applied to the precipitation forecast in the region， and the prediction results of the sliding average precipitation in the next 5 years are real and effective， respectively 508.5， 520.8， 554.9， 451.0 and 466.6 mm.

Key words： Monte Carlo method; Markov model; stochastic simulation; precipitation prediction; Yuanzhou District; K-S test

1 引 言

由于客觀世界中的一些现象可能与另一种现象存在着某种相似性，因此我们经常从一种现象出发来研究另一种现象。当某个概率模型可以描述随机系统并可以基于此概率模型进行实验时，这种实验方法即为随机模拟方法[1]。近年来，随机模拟在水文系统预测中发展迅速，取得了显著进展[2]。刘新立[3]研究了随机过程情况下随机模拟和马尔可夫链在水灾风险管理中所起的作用，研究表明两者结合可以评估未来若干个时间单位水灾所造成的风险;尹正杰等[4]提出了一个同时含有趋势、季节、随机3个分量的时间序列模型，并通过此时间序列模型对灌区灌溉需水量进行随机模拟;温季等[5]探讨了集中作物需水量的随机模拟及预测模型，结果表明随机模拟在作物灌溉管理中具有很强的应用性及普适性。

蒙特卡洛方法与马尔可夫方法在水文系统方面的应用发展十分迅速。ZHANG等[6]研究开发了基于马尔可夫链-蒙特卡洛的多级因子分析方法，从而更好地对水文模型参数不确定性进行评估;KNIGHTON等[7]通过蒙特卡洛方法将建立的概率分布应用于已知模型，用来估计水文模型的不确定性;刘悦忆等[8]在淮河流域水动力学-水质模型的基础上，使用蒙特卡洛方法随机模拟了大量入流数据并将其用作模型的输入条件进行计算，建立了基于蒙特卡洛模拟的水质概率预报模型;李娟等[9]应用滑动平均-马尔可夫模型对固原市隆德县的降水进行预测，研究证明改进后的马尔可夫模型预测精度较高;王艳等[10]在传统的马尔可夫方法上用最优分割法优化了分级标准;岳遥等[11]提出了一种基于投影距离的处理级别特征值的方法来代替传统的处理方法，并将其引入马尔可夫模型，从而应用于对水质的定量预测;李亚斌等[12]用样本均值-均方差方法对铜川地区降水量进行分级，建立相应的马尔可夫模型进行降水预测。

降水受气候和人类活动两者的共同影响，且由于气候因素本身具有很强的变异性、复杂性以及多样性，因此降水系统呈现出十分复杂的行为特征。过于复杂的系统难以建立精确的数学模型进行准确预测。笔者运用随机模拟原理，在确定地区降水的分布模型后，结合蒙特卡洛方法以及马尔可夫方法对固原市原州区的降水进行随机模拟，以期预测未来原州区降水的发展变化趋势，为水资源合理利用及调控提供依据。

2 研究方法

2.1 蒙特卡洛方法

蒙特卡洛方法又称为概率统计法，是一种基于概率论思想，对随机变量进行数理统计实验及分布概率模拟，从而近似求解得到预测值的方法[13]。只要能构建出适当的模型，此方法都能够进行模拟应用，其基本框架：①假设变量X服从某一概率分布;②用随机抽样的方法对概率分布进行抽样从而得到样本值，一般选择常用的均匀分布模型，产生（0，1）区间内的随机数，再结合原始数据产生服从特定分布的随机序列，即样本值;③确定和选取统计值;④由统计量的算术平均值得到统计量的估计值，从而近似求解出预测值。

2.2 马尔可夫方法

2.2.1 马尔可夫基本原理

马尔可夫模型是基于马尔可夫链建立起来的，马尔可夫链是一种特殊的随机过程[14]。设有一随机运动的系统，它可能处的状态记为E0、E1、…、En。这个系统只可能在时刻t（t=1，2，…，n）上改变它的状态。随着随机运动的进行，定义一列随机变量Xn（n=0，1，2，…），其中Xn=k，表示在t=n时，系统状态为Ek。

2.2.2 模糊集理论中的级别特征值

使用传统的马尔可夫只能够预测到某个区间，无法预测较为准确的降水值，在实际应用中作用有限，笔者选用模糊集理论中的级别特征值方法有效地解决了这个问题。

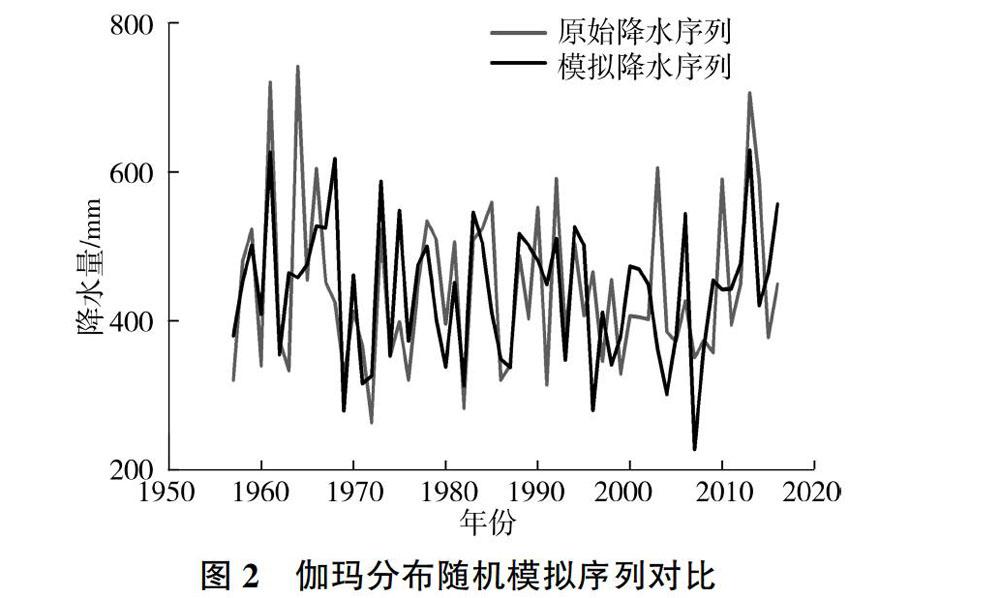
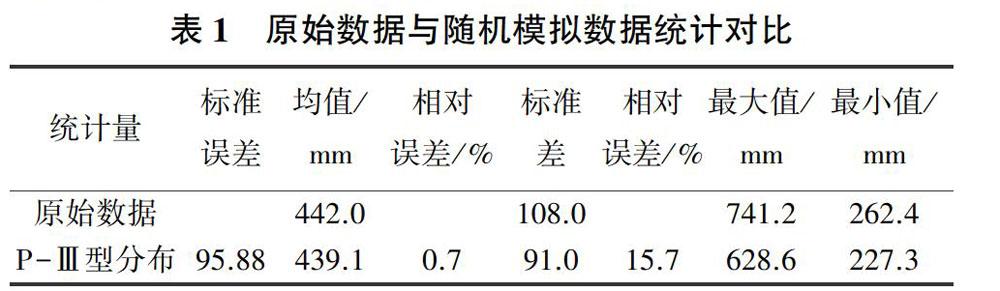
假定最大概率的状态为i，当H>i时，年降水量的预测值X预报=TiHi+0.5;当H

2.3 K-S分布檢验

K-S检验是用于检测一组数据的分布与已知分布之间相似程度的一种检验方法，通过显著性水平来判别是否相似。

设累积频率曲线的理论分布形式为Fe（x），样本的累积频率F1（x）=k/n。其中：n为总观测数，k为不大于x的次数。

3 原州区降水随机模拟分析

3.1 原州区降水量理论分布函数

根据我国水文计算的相关规范，我国主要流域的降水量可假定服从P-Ⅲ型分布或对数正态分布[15]。通过计算机软件用原始数据画频率曲线发现，当变差系数CV=0.26、偏态系数CS=0.52时，曲线模拟效果很好。又由P-Ⅲ型分布特性可知，当CS=2CV时，参数a0=0，此时的P-Ⅲ型分布就是伽玛分布，故笔者采用a0=0的P-Ⅲ型分布，即伽玛分布进行随机模拟。因为笔者主要研究降水的随机模拟，需要建立最为适合的模型，所以对两种分布进行对比，选出最贴近原始数据的分布，从而建立最优模型。

3.1.1 伽玛分布

3.1.2 对数正态分布

3.1.3 参数确定

通过原始降水数据可求得式（7）和式（8）的未知参数。由原始降水数据可知，原州区近60 a降水量的期望值为442.0 mm，方差为11 659.2 mm，从而求得对数正态分布参数μ为6.064、σ为0.234，伽玛分布中的形状参数α为14.80、尺度参数β为0.03。

3.1.4 对比分析

将原州区近60 a降水量的经验分布分别与对数正态函数理论分布及伽玛函数理论分布作对比，如图1所示。可以看出，样本数据与对数正态分布、伽玛分布的拟合效果均较好，但无法进一步判断最适合的理论分布，故笔者应用K-S检验对两者进行概率分布判断。

为了使结果更加精确，取置信度α=0.01，n=60，其K-S临界值Dα（n）为0.206 7。当假设数据服从对数正态分布时，最大偏差D（n）为0.094 1;假设数据服从伽玛分布时，最大偏差D（n）为0.107 6。通过对比分布的最大偏差与K-S检验临界值，发现两者均不能拒绝原假设，而且在99%的置信区间上符合对数正态分布及伽玛分布。由此可知，原州区降水数据既服从对数正态分布，又服从P-Ⅲ型分布。此处选取一般水文规范所用到的P-Ⅲ型分布进行随机模拟及预测研究。

3.2 降水量蒙特卡洛随机模拟

借助计算机编程，引用均匀分布模型，通过蒙特卡洛方法产生（0，1）区间的随机数，将产生的结果视为随机变量概率。为了使模拟更具可靠性，使用伽玛分布的反函数，根据原始降水序列的均值和方差，产生1 000 000组随机降水序列值。用平方误差作为评判标准，选取与原始降水序列数据平方误差最小的一组作为随机模拟降水量结果，见图2。

将原始降水序列依次与通过伽玛分布函数随机模拟出的降水序列进行对比分析。可以看出，在伽玛分布随机模拟出的新降水序列中，整体波动较大，部分极值点在时间趋势上保持一致。部分重要指标的对比见表1，伽玛分布所模拟出来的均值、标准差等指标与原始数据相差不大，模拟效果良好，进一步证明了原始数据服从P-Ⅲ型分布的结论。

3.3 马尔可夫降水预测验证

当前对马尔可夫预测准确度的评定大都是通过原始数据进行对比验证，没有考虑未来数据验证的准确性。而从随机模拟结果得到的P-Ⅲ型分布就可以很好地解决这个问题。笔者先通过对原始数据的预测及验证判别马尔可夫方法的可行性，之后再进行5 a预测，并进行K-S检验，判别其是否依旧符合P-Ⅲ型分布，从而确定预测结果的准确性。

3.3.1 分级标准及状态确定

考虑到降水序列的连续性及降水特性，采取降水序列的3 a滑动平均值进行降水预测。考虑水文现象的本身特性及序列数据的结构合理性，将降水量序列分为5类，即将降水量划分为5个区间，分别为枯水年、偏枯年、平水年、偏丰年、丰水年，采用基于欧氏距离的层次聚类法进行分级，见表2，其中x为年降水量。

3.3.3 相关系数与权重的确定

3.3.4 模型检验及分析

基于随机模拟出的2007—2011年的年降水数据，采用加权马尔可夫模型对2012年降水量进行预测，结果见表5，2012年的预测值为状态3，根据模糊集理论，级别特征值为2.824，2012年的降水量预测值为500.8 mm，相对误差为13.9%，在中长期水文预报允许误差20%之内。2013年、2014年预测值分别为521.4、499.5 mm，相对误差分别为6.5%、5.8%，都在允许误差以内。

通过以上对原始数据的验证，能在一定程度上证明加权马尔可夫模型在降水预测应用上的可行性。但是，其只能对未来降水进行预测，并不能对未来降水预测的准确性进行检验，要确保对未来预测的准确性，还需要进一步的验证。由于前文已经得到宁南地区降水符合P-Ⅲ型分布，因此笔者通过对宁南山区降水进行接下来3 a滑动平均的预测，再通过K-S检验，看是否满足P-Ⅲ型分布，预测结果见表6。

此时，n=63，取置信度α=0.01，其K-S临界值Dα（n）为0.201 8，假设数据服从P-Ⅲ型分布，最大偏差D（n）为0.080 6。通过对比分布的最大偏差与K-S检验临界值，发现不能拒绝原假设，而且在99%的置信区间上符合P-Ⅲ型分布。可见，对未来5 a的降水预测结果是可靠的。

4 结 论

（1）依据原州区1957—2016年实测降水资料，运用蒙特卡洛方法进行随机模拟，通过K-S检验，得出原州区降水符合P-Ⅲ型分布。

（2）通过对降水数据进行3 a滑动平均处理，采用基于欧氏距离的层次聚类法进行状态划分，确定了枯水年、偏枯年、正常年、偏丰年和丰水年5个状态，建立了滑动平均-加权马尔可夫链预测模型。

（3）通过对2012年、2013年、2014年滑动平均降水量的预测，得出马尔可夫降水预测模型可以应用于原州区降水预测。

（4）对未来5 a降水进行预测，预测值分别为508.5、520.8，554.9、451.0、466.6 mm，通过K-S检验进行验证，证明了预测的准确性。

参考文献：

[1] 魏艳华，王丙参.概率论与数理统计[M].成都：西南交通大学出版社，2013：264-269.

[2] 丁晶，邓育仁.随机水文学[M].成都：成都科技大学出版社，1988：9-10.

[3] 刘新立.随机过程与随机模拟在水灾风险管理中的应用研究[J].经济科学，2003（1）：114-119.

[4] 尹正杰，袁宏源，崔远来，等.灌区灌溉需水量的随机模拟[J].中国农村水利水电，2001（11）：19-22.

[5] 温季，郭树龙，卢闻航.作物灌溉随机模拟技术研究[J].人民黄河，2004，26（5）：39-41.

[6] ZHANG J L， LI Y P， HUANG G H， et al. Assessment of Parameter Uncertainty in Hydrological Model Using a Markov-Chain-Monte-Carlo-Based Multilevel-Factorial-Analysis Method[J].Journal of Hydrology， 2016， 538（7）：471-486.

[7] KNIGHTON J， WHITE E， LENNON E， et al. Development of Probability Distributions for Urban Hydrologic Model Parameters and a Monte Carlo Analysis of Model Sensitivity[J].Hydrological Processes， 2015， 28（19）：5131-5139.

[8] 刘悦忆，赵建世，黄跃飞，等.基于蒙特卡洛模拟的水质概率预报模型[J].水利学报，2015，46（1）：51-57.

[9] 李娟，张维江，马轶.滑动平均-马尔可夫模型在降水预测中的应用[J].水土保持研究，2005，12（6）：200-202，209.

[10] 王艳，毛明志，范晶，等.最优分割法确定的加权马尔可夫链在降雨量预测中的应用[J].统计与决策，2009，25（11）：17-18.

[11] 岳遥，李天宏.基于模糊集理论的马尔可夫模型在水质定量预测中的应用[J].应用基础与工程科学学报，2011，19（2）：231-242.

[12] 李亚斌，徐盼盼，钱会，等.加权马尔可夫链在铜川地区降水量预测中的应用[J].灌溉排水学报，2017，36（5）：96-102.

[13] GARCA-ALONSO C R， ARENAS-ARROYO E， PREZ-ALCAL G M. A Macro-Economic Model to Forecast Remittances Based on Monte-Carlo Simulation and Artificial Intelligence[J].Expert Systems with Applications， 2012， 39（9）：7929-7937.

[14] 夏乐天.马尔可夫链预测方法及其在水文序列中的应用研究[D].南京：河海大学，2005：11-12.

[15] 夏乐天，朱元甡.马尔可夫链预测方法的统计试验研究[J].水利学报，2007，38（增刊1）：372-378.

【責任编辑 张 帅】