刍议高中数学课堂发展学生核心素养的有效途径
2020-10-20黄维维
黄维维
[摘 要] 高中数学教师要注意核心素养理论在课堂教学中的落地生根,唯有如此,学生的核心素养发展才能得到切实的保障. 文章从教学实践出发,探讨了高中数学课堂发展学生核心素养的有效途径.
[关键词] 高中数学;核心素养;有效途径
新课程将核心素养理论作为自己的理论基础,将发展学生的核心素养作为整个教学的重心所在.高中数学教师要深度研究相关理论,并在教学实践中努力探索发展学生核心素养的有效途径.
引领学生在数学抽象中发展核心素养
数学抽象指的是研究者从数量关系或图形关系中提炼出数学概念,并探明概念之间的关系.在高中数学的课程体系中,数学抽象最重要的一个体现就是函数问题的研究,教师要善于让学生围绕函数概念进行探索,引导学生深刻经历数学抽象的过程,感悟不同层次抽象操作的思维特征,进而培养学生相关的核心素养.
从数学史的角度来看,函数的研究最早开始于人们有关动点轨迹的研究,第一次抽象在于变量的引入,此时的函数还具有较强的描述性;有关函数的第二次抽象来自映射概念的引入,这个时候的函数已经不再仅仅只是有关于对过程的刻画,映射法则的使用让函数的研究超越了表格、算式和图像的束缚,采用集合来对函数进行研究,让一切显得更加抽象;第三次抽象始于布尔巴基学派用关系来对函数进行定义,这让函数的抽象特征更加突出.
就学生来讲,上述三个层次对函数的研究其实也对应着学生素养的发展,涉及学生的几何观念、代数观念以及对应观念的培养,因此在指导学生建立函数概念时,教师要指导学生由具体事物出发展开研究,并积极展开各类抽象操作,强化对概念的理解,让他们在自主探究中明确易混淆的命题和定理,进而更加深刻地把握数学的本质性内容.
引领学生在数学思维中发展核心素养
数学是一门很强调理性思维的学科,在高中数学教学中,我们引领学生通过理性思维来分析和研究问题时,可以大幅发展学生的逻辑推理能力,合情推理与演绎推理是其最基本的两个表现形式.在数学思维的培养过程中,通过逻辑推理的教学和联系,学生的问题研究将更加有条理,思路更加清晰,各项操作也将更具合理性.
数学研究中的理性思维不是简单的思辨,它应该是研究者从观察和体验出发,强调研究者的充分经历和内化,由此实现对问题理性化的分析和探索.笔者认为,应该从两个方面来界定理性的意义,首先是判断和推理活动的理性特点,其次是控制行为的理智性,而且无论是判断,还是推理,抑或是控制行为,这些都与逻辑推理有着非常紧密的关系.
作为核心素养的重要组成,发展学生的逻辑推理能力,教师必须要向学生充分展现逻辑推理的力量,比如我們和学生探讨哥德巴赫猜想的由来和发展,让学生意识到任何通过合情推理所形成的猜想都具有一定的争议,都需要研究者进行更加严谨的探索,最后才能形成公认的结论.
数学教学过程中,教师也需要匹配一定的习题来引导学生对基本的操作细节进行熟悉,比如给学生这样一个填空题:“因为四边形ABCD是矩形,所以四边形ABCD的对角线相等. ”补充以上推理的大前提是________________. 这个问题可以引导学生对三段论实现更进一步的认识,上述问题中所提到的大前提是结论成立的依据,因此如果要根据“四边形ABCD是矩形”这句话得到其对角线相等这个结论,就一定需要一个大前提:矩形都是对角线相等的四边形.
引领学生在综合实践活动中发展核心素养
核心素养的发展离不开综合实践活动的开展,在高中数学的教学过程中,教师要善于联系实际来组织学生参加各种类型的综合实践活动,让学生能够在这个平台上充分地展现自我,并努力获得提升和发展. 在学生的整个核心素养体系中,数学建模的相关能力尤其需要综合实践活动的有序开展.
数学建模就是研究者从实际的场景出发,用数学的视角来对问题展开分析和研究,用数学语言来对问题进行表征,并最终用数学理论和相关方法完成对问题的解决. 在综合实践活动中,教师要善于为学生提供较为真实的情境,让学生能够将数学知识代入这些情境之中,展开理性而严谨的分析,这一系列过程都离不开教师有针对性的指导.
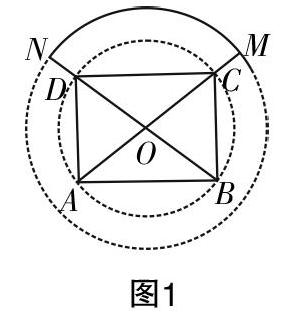
比如在城市进行新区开发时,教师从中选材,引导学生为家乡的建设献言献策,可以设计以下问题:市里准备在学校附件建一个小型公园,大概的选址是在一个以O为圆心、半径OM为3百米的圆形区域内,具体图形是如图1所示的实线及其所围成的地块,实线为道路. 图中的矩形ABCD是以O为圆心、半径OC为2百米的圆的内接矩形,点C,D分别在半径OM,ON上,设∠CAD=θ. 围绕情境,教师设计两个问题:(1)当θ=■时,求解所选地块的面积S;(2)预计该公园建成之后,可以成为当地的旅游景点,游客可以站在实线道路上观赏各种景观,根据预算,直线道路的收入每年能够达到3万元/百米,弧线道路的收入每年能够达到2■万元/百米,请分析当角度θ为何值时,可以让每年的收入W取值最大?
上述问题需要学生对实际场景进行分析,并从中提炼出相关的数量关系,建立函数模型来进行处理,具体分析如下:(1)当θ=■时,则AD=OA=OD=2,∠DOC=■π,AB=■=2■,所以所选地块的面积S=■·π·OM2+■·AD·AB+■·BC2=3π+2■+■=3π+3■. (2)由图中的几何关系可得∠COD=2θ,OM=3,NB=1+4=5,AD=4cosθ,AB=4sinθ,W=2■·■·2π·OM+3[2NB+2(AD+AB)]=12■θ+30+24■sinθ+■,θ∈0,■. 令W′=12■+24■cosθ+■=0,θ∈0,■,得θ=■. 所以x∈0,■,W′>0,W单调递增;x∈■,■,W′<0,W单调递减. 故θ=■时,每年的收入W取值最大.
引领学生在问题分析中发展核心素养
数学的研究本就是一个又一个问题的探索,我们在这里强调让学生在问题分析中获得提升,意为通过数学问题解决生成直观想象核心素养. 在不少问题研究过程中,学生往往拘泥于原有的问题框架,就对应的数学模型展开研究,这就在一定程度上捆住了自己的手脚,让他们的思维也陷于停滞. 这种情况下,教师要给予相应的启发,组织学生展开多样化的思维,在提升他们问题解决效率的同时,也能让学生感受到数学思维的巧妙.
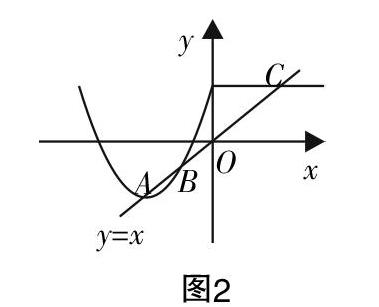
比如这样一个问题:现有分段函数f(x)=x2+bx+cx,x≤0,2,x>0,且有f(-4)=f(0),f(-2)=-2,请分析函数y=g(x)=f(x)-x的零点个数有几个.
上述问题直接探求零点的个数是非常抽象的,在实际处理过程中,教师可以加强引导让学生采用数形结合的思想来进行分析,由此来促成问题的高效解决.具体分析思路如下:先对函数方程作等价变形的处理,将其变换为两函数在某个区间存在相等解的问题,然后再利用函数图像实现解决.解答时可以这样操作:由f(-4)=f(0),可得16-4b+c=c. 又因为f(-2)=-2,可得4-2b+c=-2. 联立两方程解得:b=4,c=2.所以,f(x)=x2+4x+2,x≤0,2,x>0.在同一个坐标系内,画出函数y=f(x)与函数y=x的图像如图2所示,可以发现它们有3个交点,由此可见函数亦有3个零点.
在核心素养体系里面,直观想象能力也是非常重要的组成,在一些抽象情境的分析中,我们指导学生采用数形结合的方法来完成问题的探索,不但可以降低问题的处理难度,也可以让学生的有关素养得到发展.
