刍议现象教学理念下数学实验教学

黄雪林

[摘  要] 《普通高中数学课程标准》（2017年版）明确指出：在教学实践中，要不断探索和创新教学方式，不仅重视如何教，更要重视如何学. 有人说“教什么”比“怎么教”更重要，但“怎么教”在课堂教学中也是很重要的. 基于现象的数学实验教学不仅仅是培养了用数学的眼光观察实验现象，更多的是用数学的思维思考数学本质和用数学的语言刻画实验的数学内涵.

[关键词] 数学实验;现象教学;数学核心素养;实验探究

由于实验教学不仅在激发学生学科兴趣，培养学生观察能力、动手能力和萌发创新意识有其明显优势，还是论证理论知识和猜想的有效方式，故实验教学在自然科学学科的课堂教学中被广泛应用. 《普通高中数学课程标准》（2017年版）明确指出：在教学实践中，要不断探索和创新教学方式，不仅重视如何教，更要重视如何学，引导学生会学数学，养成良好的学习习惯;努力激发学生数学学习的兴趣，促使更多的学生热爱数学. 实验教学也在近些年进入高中数学课堂，区别于传统教学理念下数学实验课，现象教学理念下的数学实验课尽量由学生自己设计数学实验方案并动手操作，侧重于在观察直观的实验现象中自然地生成数学知识，让学生在探究过程中深度学习并实现数学核心素养的落实.

高中数学在一部分学生看来具有高度抽象、难学难懂、枯燥乏味、与实际生活无关的特征. 基于这样的影响下不少学生对高中数学的学习产生畏惧感，不想学甚至是害怕学. 在高中数学课堂教学中开展数学实验教学的目的是为了促使每一个学生都积极地参与到课堂中来，共同探究，合作思考. 数学实验课开展的实质就是帮助学生在“做数学”的过程中“学数学”.

实验案例一：探究双曲线的标准方程

爱因斯坦曾经说过：“想象比知识更重要. ”

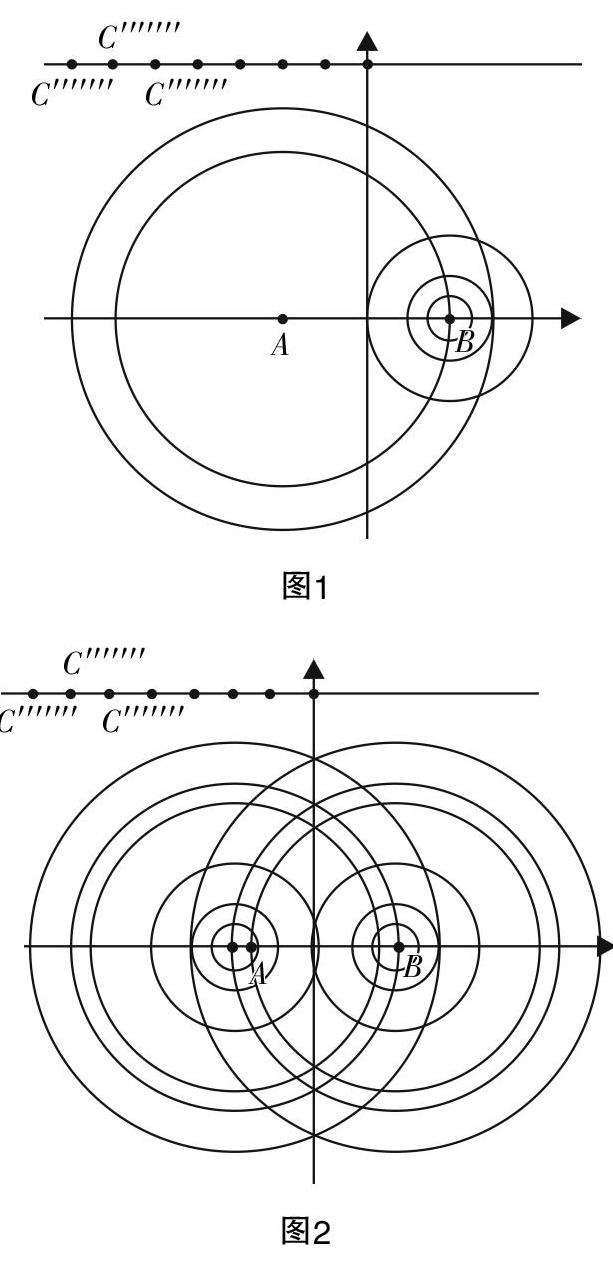
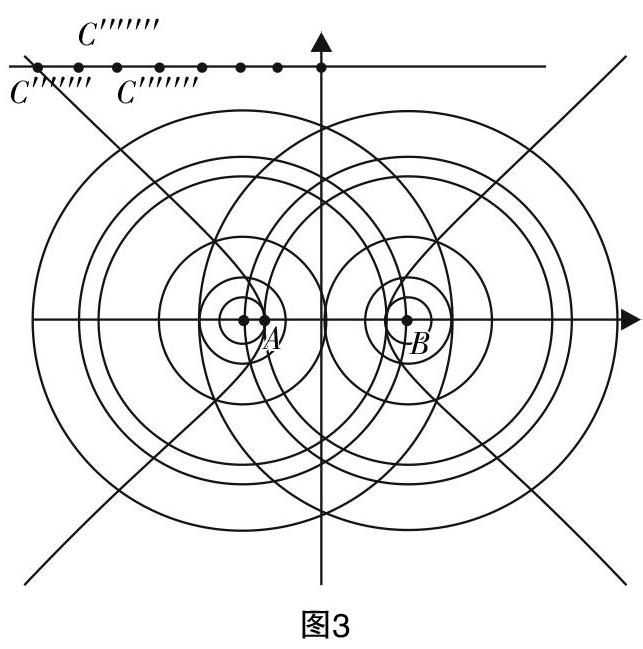
现行的高中数学教材给出的双曲线轨迹的探究基本都是“拉链模型”，作为一名初学双曲线的学生看到双曲线的定义PF1-PF2=2a（c>a>0）距离的差为定值的动点轨迹就能想到用“拉链”去探究？甚至能想到把“拉链”的一端剪去2a的长度？应该说是不太可能的，但是学生已有的基本活动经验里有没有到两定点的距离差为定值的点的轨迹模型？初中探究过中垂线的轨迹，其本质是到两定点的距离相等的点的轨迹，此时的差是定值0，其数学表达就是PF1-PF2=0. 我们能不能从探究中垂线的轨迹中得到启发制定出探求差不为0的动点轨迹，假设A，B是长为4的线段AB的两个端点，动点P到两端点的距离差是定值3，实验的设计由特殊情况出发便于培养学生特殊到一般的数学思维，更重要的是具体数值简化探究. 回顾了中垂线的探究过程，学生能够自然地生成尺规探究的设计方案. 以A，B为圆心画圆，半径为r1，r2，且r1-r2=3，改变圆的半径，两圆的交点就是使得PA-PB=3的动点. （实验活动过程可以使用实验网格纸，尺规画图探究;也可以利用几何画板探究.）个人建议学生使用尺规作图探究，经历自主探究的过程可以实现深化实验现象的数学化，图像本身的探究就是双曲线概念、方程和性质的直观化过程.

数学实验的设计不应该脱离学生的基本活动经验，“从天而降”的活动情景不利于学生对新知识的自然生成. 尺规探究双曲线的轨迹是建立在学生已掌握了中垂线的定义和图像、圆的标准方程和性质、椭圆的标准方程和性质，这些知识都可以帮助学生自然地构建两圆半径差为定值的交点的探究方案. 由具体的数值（特殊化）易于构建的特征方便学生完成实验的操作，无形中形成特殊到一般的数学素养.

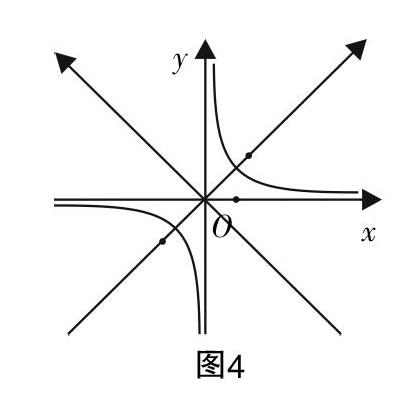
教师可以进一步提出能不能探究初中学习过的反比例函数图像，和高中学习的双曲线是不是一回事？以y=■为例. 实验进一步深化对双曲线概念理解，坐标系是人类赋予双曲线的，人类建立的坐标系不同双曲线的方程形式也会发生改变，反比例函数是双曲线建系方式发生改变的情况下的方程形式. 通过这样的方式真正实现初中知识与高中知识的整合，绽放核心素养之花.

实验案例二：变量A，ω，φ与函数y=Asin（ωx+φ）图像的关系

弗赖登塔尔曾经说过“数学知识既不是教出来的，也不是学出来的，而是研究出来的.”本课题开展前学生已有的基本活动经验是“五点法”绘制三角函数的图像，在研究本课题时可以理解y=sinx是A=1，ω=1，φ=0时y=Asin（ωx+φ）的特殊形式. 学会控制变量，在研究参量A，ω，φ对函数图像的关系显得非常重要.

学生可以应用已学的“五点法”手工作图研究参量对函数的影响. 考虑到“五点法”手工作图非常耗时，并且在研究过程中也很不方便，大部分学生都存在作图不标准的情况，对于实验研究来说是非常不利的. 如何设计这个实验案例，能让枯燥的课堂生动有趣起来？让学生能够在获取数学新知的同时真实地感受到数学实验探究的快乐.

由于本节课探究的是参量A，ω，φ对函数图像的关系，通过实验的探究获取参量与图像平移、翻折间的关系. 在实验探究的过程中可以使用几何画板和EXCEL等作图软件辅助完成作图过程，搭建实验研究平台.

控制变量是本实验的主要设计思路，分组设计变量A，ω，φ进行实验的探究活动. 设计三组实验数据进行简单的探究活动y=sinx，y=2sinx，y=■sinx，y=sinx，y=sin2x，y=sin■，y=sinx，y=sinx-■，y=sinx+■.初步感知變量A，ω，φ与正弦函数图像的关系. 直接利用几何画板演示y=sinx→y=sin2x→y=sin2x+■→y=2sin2x+■和y=sinx→y= sinx+■→y=sin2x+■→y= 2sin2x+■的变化过程，并让学生归纳两个变化过程的相同点与不同点. 这样的实验探究活动对学生理解变量A，ω，φ与正弦函数图像的关系与“满堂灌”的效果肯定是不一样的.

实验案例三：同角三角函数的关系

欧拉曾说：“今天人们所知道的数学的知识，很多都是由观察所发现的，并且早在用严格论证确认其真实性之前就发现了，甚至到现在还有许多关于数学的知识是我们所熟悉而不能证明的，只有观察才使我们知道这些知识. ”

在人类文明不断进步发展的过程中，数学实验对数学学科发展的前进起着巨大的推动作用，人类早期的很多数学结论和定理都是通过实验得出的. 数学家们常常在数学实验的帮助下发现新的数学规律和新的数学公式，再通过对实验结果进行严格的逻辑演绎推理，给出证明. 可以这样说在人类的数学的发现中，数学实验肩负着重要的发现作用.

在研究同角三角函数的关系时，学生已有的数学知识是初中学习的直角三角形中的锐角三角函数并且掌握得非常好，最近发展区中还有任意角的概念（将三角形中的角扩充到直角坐标系中研究角）和任意角三角函数的概念.

教师抛出问题：已知sinα=■，请你设计方案解决cosα和tanα.

学生分组给出的实验方案主要分为几何探究和代数探究两个方向，几何探究有建立直角三角形（勾三股四弦五）的不完全探究，根据任意角和三角函数的定义建立直角坐标系探究的不同方案. 经历过直角三角形的不完全探究，能够深化理解任意角和任意角的三角函数的概念，效果显然优于教师单方面的灌输. 再进一步引导学生由特殊值向一般情况探究，由特殊点P（4，3）或P（-4，3）到P（x，y）是否也存在sin2α+cos2α=1的关系？学生依然有几何探究的方案，直接在几何画板中计算探究;也可以根据任意角三角函数定义进行代数探究，sin2α+cos2α=■■+■■=1. 教师可以提出单位圆中正弦线和余弦线的几何意义对几何方案进行优化，单位圆中的任意一点P（x，y）也可以表述为P（cosα，sinα）到坐标原点的距离都是1，根据两点间的距离公式快速得到sin2α+cos2α=1. 在深化理解了sin2α+cos2α=1后，学生同样可以從几何和代数两个方向探究出tanα=■，其效果明显优于传统教学方式.

实验教学的最大特点是数学现象的直观性，帮助学生对源于生活的素材进行数学研究，实现生活素材“数学化”和“再创造”，对源于生活的数学知识的研究有利于激发学生学习数学的热情. 现象教学理念下的实验教学不是一个简单的知识传输过程，也不是一个被动的回答问题过程，而是真实地帮助学生“用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达世界”（史宁中）. 亲身经历对数学现象的迷茫、疑惑、猜想、试验、论证、表达等过程，是知识教学和问题教学所难以比拟的. 学生所生成的基本活动经验、数学应用意识等等，比具体的知识和技能更有价值，这些就应该是学生“把教材内容都忘记后还剩下的部分”（爱因斯坦），也可以说这些就是核心素养.

数学实验教学是现象教学的一种表现形式，是对数学课堂教学有效的补充与促进，而不是替代和否定. 现象教学在针对不同类型的知识教学上有不同的教学手段，其独特的优势表现在使用非常灵活且广泛. 开展实验教学可以起到“画龙点睛”的作用，而不是“画蛇添足”. 在教学中，充分发挥数学实验的优势，注意扬长避短，实现信息技术和数学教学合理的整合. 数学实验课程的开设在中学阶段还是一个较为新颖的事物，需要广大中学数学教师对其不断研究和实践. 我们不难发现，无论是新授课的导入、关键知识点的讲授、研究性学习的指导，数学实验课程都发挥着重要的建设性作用，并且在《普通高中课程标准》（2017年版）中给出了不少数学实验课程的优秀课例. 我校尝试在现象教学模式下开设数学实验课对推进高中数学核心素养的落实具有的创新意义，并为高中数学实验课程开辟出自己的舞台.