基于Hermite插值改进的轨迹修正滤波算法

丁志伟 陈泽宇 马梦园 张正军

摘   要：借助移动物体轨迹上标定的真实值点的位置信息和方向信息，构造分段三次Hermite插值函数，对标准卡尔曼滤波和标准粒子滤波的状态方程进行修正，得到两种改进滤波模型，解决了标准滤波算法中状态方程不能准确刻画物体实际运动轨迹的问题。在实验分析中对定常速曲线运动物体的位置坐标进行滤波修正，位置坐标的均方误差分析表明，卡尔曼滤波算法和粒子滤波算法的滤波效果均有改善，其中卡尔曼滤波算法在精度上明显提高。此外，真实值点数量的灵敏度分析的结果表明，在目标轨迹上取少量且关键的点作为真实值点即可达到明显的修正效果。

关键词：卡尔曼滤波;粒子滤波;真实值;Hermite插值

中图分类号： TN713;P228.4                              文獻标识码：A

Implementing Filtering Algorithm Refined

by Hermite Interpolation in Track Revision

DING Zhi-wei?，CHEN Ze-yu，MA Meng-yuan，ZHANG Zheng-jun

（School of Science，Nanjing University of Science and Technology，Nanjing，Jiangsu 210094，China）

Abstract：Through the position and direction information of the real value points on object track，a piecewise cubic Hermite interpolation function is constructed to modify the state equation of standard Kalman filter and standard particle filter. The state equation in standard filter algorithm can describe the actual trajectory of specific object more accurately. In the experimental analysis，the track of the object with constant velocity in curvilinear motion is revised. The mean square error of the position coordinates demonstrates that the improvement of Kalman filter algorithm and particle filter algorithm is practical. Moreover，Kalman filter algorithm is improved more significantly in position accuracy. Besides，the sensitivity analysis about the number of real points shows that a proper number of key points on the target track can be regarded as real points to achieve expected accuracy.

Key words：Kalman filter;particle filter;real value;Hermite interpolation

随着卫星定位技术和计算机技术的发展，移动物体轨迹的应用也日益广泛，如车辆异常状态的分析、车辆的动态轨迹预测等[1]。但由于 GPS 定位受到多种误差的影响[2-3]，极大限制了高精度实时定位的应用。

在动态轨迹修正领域，常用的技术有标准卡尔曼滤波和标准粒子滤波。虽然它们的可行性已经得到研究的验证[4-5]，但在实际应用中滤波算法会产生精度不高、滤波发散等问题。当前国内外针对标准滤波算法的不足，已经提出了一系列的改进算法。

在提高卡尔曼滤波算法的精度方面，学者们从不同角度提出基于卡尔曼滤波的改进算法，如结合最小二乘法的卡尔曼滤波算法[6]，运用位置差分方法提出带速度约束条件的卡尔曼滤波算法和扩展卡尔曼滤波等[7-8]。还有学者通过修正状态方程中的误差项以改善滤波效果[9]。为了避免滤波发散，有学者提出一种渐消因子改进算法，实现卡尔曼滤波的自适应[10]。作为粒子滤波算法的主要缺陷，粒子退化问题受到学者的广泛讨论与研究，解决该问题最有效的方法是选择好重要性概率密度函数或采用重采样方法。在提高粒子滤波实时性的方面，有学者提出自适应粒子滤波（APF）和实时粒子滤波（RTPF）等改进算法[11]。

标准卡尔曼滤波方法中使用的线性模型不能刻画物体的某些复杂曲线运动，虽然一些基于非线性模型的改进卡尔曼滤波算法和部分改进的粒子滤波算法能够解决该问题，但这些方法较为复杂，且无法达到某些应用领域的要求。因此，需要一种较为简便的滤波方法，继续使用线性模型来描述动态运动，并尽可能缩小误差范围，保证滤波的效果。

提出了一种基于真实值点构造分段三次Hermite插值函数的改进思路，将其运用于标准卡尔曼滤波和标准粒子滤波，分别得到两种改进的滤波算法。该类算法通过Hermite插值函数近似移动物体的真实轨迹，达到滤波预测值更接近真实情况的目的。实验结果表明，卡尔曼滤波算法和粒子滤波算法的滤波效果均有改善，其中卡尔曼滤波的改进效果尤为显著。与先前的研究相比，上述方法简便易行，对于移动物体的轨迹修正精度有显著提高。

1   移动物体的运动学模型

在BJ-54坐标系下，考虑物体的定常速曲线运动模型，以物体的位置和速度作为状态变量，并假定系统噪声和测量噪声均为高斯白噪声。设物体的状态向量为Xt = [xt   yt   vx，t   vy，t]T。其中，xt、yt分别为t时刻物体所在位置的BJ-54横坐标、纵坐标;vx，t、vy，t分别为t时刻物体在横坐标轴、纵坐标轴方向上的速度。

此时，状态方程为：

式中，At|t-1为从t-1时刻到t时刻的状态转移矩阵。

状态转移矩阵和噪声驱动矩阵分别为[12]：

式中，ωt為t时刻目标物体的角速度;dT为GPS采样的时间间隔。

观测方程为：

Zt = HXt + νt（4）

式中，Zt为观测向量;H为测量矩阵，H = I4 为4阶单位矩阵。

2   标准滤波模型及算法

2.1   标准卡尔曼滤波算法

标准卡尔曼滤波算法是基于状态空间的一套递推滤波算法，它主要包括状态方程和观测方程。标准卡尔曼滤波过程主要由以下公式组成：

式中，At|t-1为状态转移矩阵;[^][X]t为t时刻状态向量的滤波估计值;[^][P]t为t时刻误差的协方差矩阵;Q = σ2

uBBT为系统噪声的协方差矩阵;R为测量噪声的协方差矩阵;Kt为t时刻的卡尔曼滤波增益值。

2.2   标准粒子滤波算法

标准粒子滤波算法是一种基于贝叶斯理论和蒙特卡罗方法的统计滤波算法。其基本思想是先在状态空间中产生一组加权随机样本（粒子），然后在测量数据的基础上通过调节粒子的权重大小来获得服从实际分布的样本，并以样本均值作为系统状态的估计值。

粒子滤波的具体实现步骤如下[11，13]：

Step1：初始化k = 0，采样xi

0 ～ p（x0），即根据分布p（x0）采样得到xi

Step2：重要性权值计算。设定k ：= k + 1，采样xi

重要性权值计算如下：

Step5：判断是否结束，若是则退出本算法，若否则返回Step2。

3   改进的滤波算法

3.1   改进的思路

上述两种滤波算法均利用状态转移矩阵At|t-1刻画移动物体从t-1时刻到t时刻的状态变化，并结合实际观测值Zt，求得t时刻滤波预测值[^][X]t，再让 [^][X]t参与下一步的迭代。但在实际应用中路况复杂，运动学公式无法准确描述移动物体的实际运动轨迹，从而经滤波后得到的轨迹与实际轨迹有较大偏移。考虑到应用中存在上述不足，本文提出一种改进思路应用于滤波算法，用作移动物体的轨迹修正。事实上，物体的移动轨迹上存在一些关键点，如连续转向点。而这些转向点一般存在于特殊路段如十字路口、高速的匝道等，该处经纬度可以事先精确测量。

基于上述考虑，给定移动物体轨迹上的n个已知经纬度坐标的真实值点列S = {Pi|i = 1，2，…，n}，利用分段插值方法做出一段曲线，再将由运动学公式计算得到的t时刻位置的横坐标xi代入插值曲线方程，可以计算出预测的真实值点的纵坐标yi*。然后，对（xi，yi）和（xi，yi*）经过加权修正得到（xi，[y][～]i）以减少运动学公式利用带来的误差。最后，将（xi，

[y][～]i）作为修正后的理论值中间变量代入滤波过程，可求得修正后的滤波预测值（[x][^]i，[y][^]i）。

改进滤波算法的具体思路见图1。

3.2   真实值点列的选择

针对定常速曲线运动情形，主要选取在方向发生较大变化的拐点、周围存在较多的随机因素的路口等位置。Hermite插值方法需要区间端点的位置和导数值，本文用待求点的一阶差商作为该点导数值的近似替代，在实际算法中，只需再一个构造辅助的真实点列[S][～] = {[P][～]i|i = 1，2，…，n}。

对Pi和[P][～]i的坐标作差商，将得到的结果作为真实值点Pi的导数值，用于插值函数的构造。实际应用中可以借助于速度传感器等设备搜集一阶导数信息，不必依赖真实值点。只是在本研究中受限于仪器设备，故作该处理，因此后文在统计所需真实值点的数目时，未将辅助点数目纳入其中。引入真实值点列具有重要意义：根据点的选取原则，真实值点列为轨迹上关键的，或者测量中容易发生偏移的位置。那么，运用点列信息后就可以减少点列附近测量数据的偏移。在上述方法中，还需指出，仅利用插值函数修正理论值中间变量的位置信息，对于速度和方向没有改动。

3.3   分段三次Hermite插值

设真实轨迹函数为fi（x），i = 1，2，…，n，相邻两个真实值点Pi和Pi+1的BJ-54坐标为（xi

式中，α1和α2为权重因子，分别衡量对状态方程和真实值点的依赖程度。当α1 = 1，α2 = 0时，退化为标准滤波算法。一般地，α1和α2在（0，1）内取值。

3.4   Hermite-KF算法（HKF）

HKF算法过程主要由以下公式组成：

式中，Xt*为修正后的理论值，其它符号的含义同前。

HKF的主要步骤如下：

Step1：参数值的初始化：给定初始状态X0，误差协方差矩阵初值P0 = I4，其中I4为四阶单位矩阵;系统噪声的协方差矩阵Q = 10-3 × BBT;测量噪声的协方差矩阵R为对角矩阵，可由单点定位误差的方差和速度的测量方差得到;

Step2：状态更新：根据t - 1时刻的预测状态[^][X]t 结合状态方程计算第t时刻的状态Xt;

Step3：加权修正：根据第二步中Xt确定位置区间和运动方向，寻找对应的插值区间，并运用Hermit插值法计算插值函数的函数值H（Xt），用算术平均修正位置信息，得到修正后的状态量Xt*;

Step4：误差更新：根据第t - 1时刻的过程预测误差[^][P]t估计t时刻的过程预测误差[P][～]t;

Step5：增益计算：计算卡尔曼增益Kt;

Step6：滤波预测：结合实际观测值计算系统最优估算值[^][X]t;

Step7：误差预测：计算系统当前时刻的系统预测误差[^][P]t。

3.5   Hermite-PF算法（HPF）

HPF算法的状态方程和观测方程分别为：

Xt* = F（At|t-1 [^][X]t-1 ） + But - 1

Zt = HXt + νt（10）

其余迭代步骤同前。

4   实验与分析

4.1   实验设计

实验选取ATGM332D双模接收机作为GPS数据接收工具，结合自行编写的BD-GPS数据采集系统对卫星数据进行解码，获取经纬度、海拔高度及速度等信息。在南京奥体中心进行实地实验，对定位数据分别采用KF、HKF、PF、HPF进行滤波。实验结果以均方根誤差作为评价标准，衡量滤波算法的改善效果，并对真实值点列个数进行灵敏度分析。

改进的滤波算法中真实值点列经纬度坐标的确定：在轨迹上取12个关键点，每个点用GPS接收机采集1000个经纬度定位数据，后进行单点滤波[15]，将滤波的平均值作为真实值对应的经纬度。

4.2   数据预处理

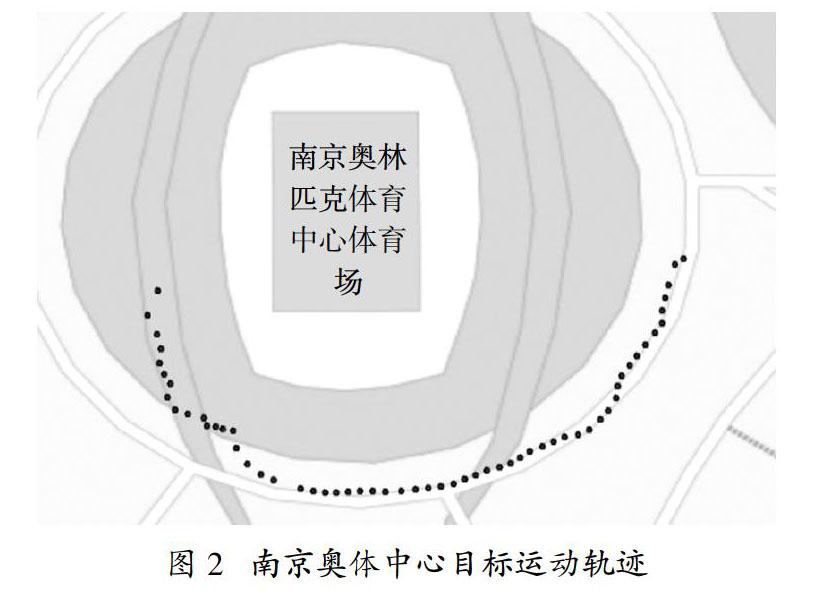
首先剔除野点。由于运动模型中采用XY坐标而非经纬度，因此需要进行坐标变换[16-17]。图2是南京奥体中心经纬度数据转换后的物体运动轨迹。

4.3   实验结果及分析

4.3.1   滤波算法的效果比较

在定常速曲线运动情形下，分别利用KF、HKF、PF、HPF对定位数据进行修正，这里借助的真实值点的数目为7。

图3中的a，b，c，d分别为KF、HKF、PF、HPF的滤波效果图。图中theoretical表示理论公式计算得到的坐标;metrical表示实际测量值;estimated表示滤波估计的位置坐标。不难看出，相比于标准算法，两种改进滤波算法的理论值与实际值更加接近，这是引入真实值点阵修正后的效果，更加准确地刻画实际测量中的道路轨迹，进而可以达到让滤波更为准确的目的。

进一步地，将滤波结果同真实值相比，分别做出两种滤波下x坐标和y坐标的误差图，见图3中e，f，g，h。可以看到，HKF的误差较KF有显著减小;HPF在y方向上误差较PF有显著减小，在x方向上有些许增大。总体来说，两种算法的误差均有减小。这一点也可以从两种滤波方法下位置坐标的均方根误差中看出，根据均方根误差计算式：

RMSEx = ，（11）

RMSEy = .（12）

得在四种滤波下的x、y方向上的均方误差，见表1。

由表1知，卡尔曼滤波算法和粒子滤波算法均有改进。

4.3.2   灵敏度分析

对于改进的滤波方法，真实值点的数量与误差减小之间需要进行权衡。如果所需要的点数过多，那么前期采集真实值的工作量就变得庞大，改进滤波方法的实用价值自然也就不大。因此，以下针对真实值点的个数进行灵敏度分析。

图4是HKF和HPF在x、y方向上偏移量示意图，横坐标表示时间，纵坐标表示对应时刻真实点和滤波预测点坐标的偏移量。对于HKF，不同的真实值点数对于x、y方向的误差影响较小;对于HPF，除了在5个真实值点时由于真实值点数量太少导致y坐标误差较大外，借助多于8个真实值点时x、y方向上误差均在（-5，15）内波动，这说明真实值点的数量对于误差的减小效果并不敏感。

计算在不同真实值点数下两种改进滤波的均方根误差，见表2和表3。结果表明，随着真实值点数目的增加，均方根误差总体上呈减小趋势，但效果不明显，这表明在运用中，只需要依赖较少的真实点，就可以达到减小定位误差的目的。

研究还表明，当真实值点取在道路上的关键点，比如轨迹的起始点、终点和拐点的时候，滤波效果更好，均方根误差更小。针对选用7个真实值点

研究还表明，当真实值点取在道路上的关键点，比如轨迹的起始点、终点和拐点的时候，滤波效果更好，均方根误差更小。针对选用7个真实值点时，在对所取点的位置进行分析后得出，选取关键点可以显著降低误差，效果甚至优于借助更多的真实值点，改进卡尔曼滤波的效果见表4。

表4   不同取点位置下HKF的误差比较

[点列数 7点 7点关键点 RMSEx /m 4.488 8 4.487 5 RMSEy /m 3.498 2 3.480 2 ]

5   结   论

对标准滤波算法进行优化，在状态方程中融入由真实值点列构成的插值多项式，根据物体的运动方式，对插值多项式和运动学公式选取不同的权值，改进状态方程，使得对下一时刻状态的估计更加精确。实验结果表明，借助于移动物体轨迹上较少的关键位置的真实点，改进卡尔曼滤波算法和改进粒子滤波算法可以实现对一段轨迹的经纬度的修正，且在精度上相比标准算法得到了提高。在实际应用中，只需事先在计划轨迹上标定真实点，以后无需标定。该方法成本低、效果好。但是受限于时间和经费，没有进行大量的实验，仅仅对定常速曲线运动情况进行了分析，对于更一般的运动形式有待进一步分析。

参考文献

[1]    陈志军，吴超仲，吕能超，等. 基于改进三次Hermite插值的车辆时空轨迹重构研究[J]. 交通信息与安全，2013，31（6）：43-46.

[2]    ELLIOT D K，CHRISTOPHER J H. GPS原理与应用[M]. 寇艳红，译. 北京：电子工业出版社，2007.

[3]    刘基余，李征航，王跃虎，等. 全球定位系统原理及应用[M]. 北京：测绘出版社，1993.

[4]    刘婵媛，陈国光. 基于GPS的卡尔曼滤波技术研究[J]. 弹箭与制导学报，2006，26（4）：110-112.

[5]    张堑，高天德. 基于GPS的动态目标定位滤波方法[J]. 计算机仿真，2012，29（5）：319-321，337.

[6]    陳鹏，钱徽，朱淼良.基于加权最小二乘的卡尔曼滤波算法[J]. 计算机科学，2009，36（11）：230-231，257.

[7]    陈宝远，孙宇思，陈光毅，等. 一种基于卡尔曼滤波的动态目标GPS定位算法[J]. 哈尔滨理工大学学报，2016，21（4）：1-6.

[8]    林雪原，骆卉子，范文强. 一种改进的GPS动态定位滤波方法[J]. 海军航空工程学院学报，2010，25（4）：361-364.

[9]    宋迎春. 动态定位中的卡尔曼滤波研究[D]. 长沙：中南大学，2008.

[10]  蔡艳辉，程鹏飞，李夕银.用卡尔曼滤波进行GPS动态定位[J]. 测绘通报，2006（7）：6-8.

[11]  朱志宇. 粒子滤波算法及其应用[M]. 北京：科学出版社，2010.

[12] ACHUTEGUI K，RRODAS J，ESCUDERO C J，et al. Bayesian filtering methods for target tracking in mixed indoor/outdoor environments[C]. International Conference on Mobile Lightweight Wireless Systems，2012：169-185.

[13]  胡洪涛，敬忠良，李安平，等. 非高斯条件下基于粒子滤波的目标跟踪[J]. 上海交通大学学报，2004，38（12）：1996-1999.

[14]  关冶，陆金甫.数值分析基础（第二版）[M]. 北京：高等教育出版社，2010.

[15]  孙罡，王昌明，张爱军. GPS静态单点定位的滤波算法比较[J]. 南京理工大学学报（自然科学版），2011，35（1）：80-85.

[16]  王解先，王军，陆彩萍. GPS测定坐标转换至地方坐标[J]. 全球定位系统，2003，28（4）：7-10.

[17]  蒋小军，宋占峰，吴清华. 地方独立坐标系与WGS-84坐标系转换方法及应用[J]. 铁道勘察，2010，36（4）：8-10，13.