基于随机森林与卷积神经网络的电力负荷预测研究
2020-10-20肖玉东
肖玉东


摘 要:针对电力负荷预测模型中变量冗余与拟合性能不佳问题,提出了应用随机森林(RF)筛选最优输入变量并结合卷积神经网络(CNN)的电力负荷预测模型。实证显示,经RF变量优选后模型平均MAE减少2.49%,EMSE减少3.40%;基于CNN神预测模型的平均MAE与RMSE分别降低了1.33%、2.46%。采用RF与CNN集成的方法具有最高的预测精度,其MAE为3.46%,RMSE为4.08%,该模型性能优于其他组合方案,是电荷预测精准建模的一种可靠方案。
关键词:随机森林;卷积神经网络;变量优选;建模预测;电力负荷
中图分类号:TP319 文献标识码:A
Research on Power Load Forecasting Based
on Random Forest and Convolution Neural Network
XIAO Yu-dong?
(Turpan Vocational and Technical College,Turpan,Xinjiang 838000,China)
Absrtact:In order to solve the problem of variable redundancy and poor fitting performance in power load forecasting model,a power load forecasting model is proposed,which uses random forest(RF) to select the optimal input variables and convolution neural network (CNN). The empirical results show that the average Mae and EMSE decrease by 2.49% and 3.40% respectively after RF variable optimization,and the average Mae and RMSE decrease by 1.33% and 2.46% respectively based on CNN prediction model. The integration method of RF and CNN has the highest prediction accuracy,with MAE of 3.46% and RMSE of 4.08%. The performance of the model is better than other combination schemes,and it is a reliable scheme for accurate charge prediction modeling.
Key words:random forest;convolution neural network;variable optimization;modeling and forecasting;power load
電力负荷时序变化是经济水平、人口、气象环境等因素非线性综合影响的结果,其既保留了历史电荷信息反馈特征,还受外部动态因素影响而表现出随机性,因此常规数学模型难以拟合其精确演变规律[1]。随着数据挖掘技术的深入推广,智能化算法取代传统统计学方法成为电力大数据信息提取的关键技术之一[2]。卷积神经网络(Convolutional Neural Network,CNN)是一种基于前向传播的深层神经网络,相较于传统的神经网络,它引入了卷积和池化运算,其能够协调历史单元信息将其反馈于前向预测,并被广泛应用于目标检测、文本分类、图像处理、场景分析等领域[3],然而在电荷预测研究中尚不多见。
输入变量对电荷预测模型的泛化能力具有显著影响。对此,相关学者提出了人工与客观筛选法,前者受主观臆断限制难以取得普遍应用效果。目前较为常见的客观选择法有主成分分析[4]、灰色关联分析[5]、聚类分析[6]、投影寻踪法[7]等,其能够避免主观影响,却仍未能规避变量的高度相关、共线性、信息冗余等问题,导致数据噪声影响了模型精度。鉴于此,相关工作者提出了模拟退火[8]、粒子群[9]、贝叶斯[10]等智能搜索法,通过寻找预测误差最小的变量方法确定输入变量集,而该类封装算法结构复杂,容易陷入局部极小问题。随机森林通过自主学习、高维映射、容错等手段大量挖掘隐含信息,能够排除噪声、共线性影响,对高维非线性、非结构化问题具有良好的自适应能力,从而更加客观地识别单一变量对预测模型的影响[11]。本研究拟采用RF原理在对输入变量进行无偏优选的基础上,结合CNN算法构建电力负荷预测模型,并证明该方案的有效性。
1 随机森林变量选择
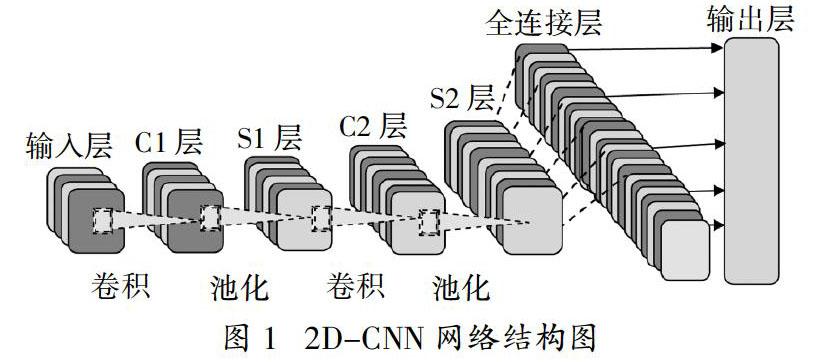
随机森林(Random Forest,RF)基于随机子空间理论和bootstrap方法对向量(X,Y){Θn,k = 1,2,…,N}随机选抽取并进行树形生长成为决策树,每棵树给出最优分类结果,最后结果为K棵树中投票最多的选项[11]。设电荷数据训练数据(X,Y)含n个样本,随机放回抽取b个子集构建回归树,当抽取第i(i∈b)个子集时未被抽取的样本为袋外(out of bag,oob)数据,另从M维矢量中选取固定维数为m(m 式中,I为最优分裂变量,s为嵌入样本维数;Xs、Xs′分别表示变量的值与平均值。完成树形生长后构成随机森林,进而计算袋外数据对模型的影响: 式中,MSE为均方残差;n表示袋外数据样本量;yi和yi′分别表示第i组样本的真实电荷值与预测值。RF模型通过均方残差减小量表征输入变量的重要性,利用袋外数据生成K棵回归树得到均方残差序列为[MSE1,MSE2,……,MSEK],多次抽样后生成新的K棵回归树,构成袋外数据残差矩阵。对于第m个输入变量,其重要性度量如下: 式中,Vim为变量重要性分值,k为决策树个数,j∈k,SE为k棵决策树标准误差[11]。 2 卷积神经网络 CNN由输入层、卷积层、池化层、全连接层、输出层组成的多层次网络结构[12]。其采用局部连接与权重共享方式对原始数据矩阵进行高维变换与抽象处理,可基于数据集特征构建不同维度结构模型,其使用的卷积和池化层运算有效自动提取数据特征向量,降低了数据重构复杂度并增强特征量。研究表明,2D-CNN网络较适用于变量维度与长度并不繁杂的数据集[12],因此选择2D-CNN网络作为建模技术,其结构如图1。 输入层用于接收多维原始变量X[x1,x2,…,xt-1,xt··· xn]T以便在网络中处理。 卷积层通过对输入向量、权重和偏置进行点积乘法运算来提取输入特征,然后应用激活函数进行非线性映射,池化层基于空间维度的采样算子来降低要素维数,并提取输入特征,其运算如下: 式中C1、C2分别为卷积层1、卷积层2的输出向量;p1、p2依次为池化层1、池化层2的输出;w1、w2、w3为权重矩阵,b1、b2、b3、b4、b5为偏置向量;卷积与池化运算后的输出为Hc = [hc1,hc2,…,hct-1,hct,…hci]T,i为输出序列长度,Relu、Sigmoid、指数函数为激活函数[2]。 全连接层由神经元组构成,其利用激活函数对特征向量进行权重分配,并迭代更新出较优的权重参数矩阵。 激活函数从所提取的特征中学习负荷变化规律以实现预测功能,并通过输出层得到仿真结果。输出层计算公式为: 式中yt为第t次网络训练输出结果,wo、bo分别为权重矩阵、偏置向量,Relu为输出层的激活函数[11]。 3 算例分析 3.1 數据来源与误差评价 采用中国南方某地区的2019年3月5日至27日的实际电力负荷数据集进行实验。数据采集频率为15 min/次,时间间隔为1 h,此外基于标准气象台站同步记录了气象数据,包含气温、气压、空气湿度、风速等指标。基于文献[2,13],选择部分历史负荷序列与气象数据为协变量(表1)。 备选的协变量众多,为消除量纲差异减少数据噪声,采用极差标准化方法将变量进行归一化处理,公式如下: 式中,yij为第i个变量第j个样本的标准化值;xij为其原始值;xmax i、xmin i分别表示第i个变量所有样本中的最大、最小值。 为衡量电力负荷模拟精度,采用平均绝对误差 (mean absolute error,MAE)百分数和均方根误差(root mean square error,RMSE)作为评价指标,计算公式如下: 式中,n为测试样本个数;yi、yi′分别表示第i时刻负荷实际值与预测值。通常,MAE和RMSE的值越小,表明预测值越接近实际值,模型精度越高。 3.2 随机森林变量选择 依图2可知,预选的24个变量中有u、v、w、q、a、e、j、c、b、r、x、s、d、g等14个变量的重要性分值介于2.42~15.20,而变量i、m、y、t、f、h、n、l、p、o、d的分值在-2.12~0.07之间,后者未通过5%信度检验的变量,对模型影响微弱。综合而言,预测误差随着变量增加逐渐减少,说明嵌入维数较多利于模型平稳性,对预测精度有所提升;但变量增加至14个以上时,预测误差略有回升,说明输入矢量过多,使模型结构更为复杂,冗余信息影响了泛化效率。因此,选择u等14个变量作为输入变量,其他变量予以剔除。 3.3 基于CNN电力负荷预测模型构建 利用RstudioVension 1.102开源软件和RandmForest、Keras、Tensorflow程序包设计变量选择与电力负荷预测模型。优选的最佳变量子集经归一化后转置为4-D矩阵,大小n×c×w×h,其中n表示训练集或测试集数量,c为协变量数,w、h为输入变量像素,且w = h。将数据集划分为2部分,3月2日至25日的数据为训练样本,26-27日数据为测试样本,运用CNN网络模型进行学习训练。利用格网搜索法调整CNN模型的激活函数、卷积核、每层节点数、迭代次数等参数[12],参数设置如表2。 表2 基于CNN的电力负荷预测模型的网络结构参数 [网络层次 卷积核 神经元个数 激活函数 卷积层1 (2,2) 64 Relu 池化层1 (2,2) — Max 卷积层2 (2,2) 128 Relu 池化层2 (2,2) — Max 全连接层1 — 500 Relu 全连接层2 — 1 Relu ] 注:该CNN网络结构参数为经协变量筛选之后的电力负荷预测模型。 3.4 结果分析及比较 图3为基于CNN模型得到的电力负荷预测结果,为验证算法有效性,另外运用经典的RF回归对测试样本进行预测,比较其与CNN模型性能(图3和表3)。 从表3中可直观地看出,CNN与RF模型预测结果基本符合实际电力负荷变化,预测值与实际值拟合良好,异常值较少。从算法角度来看,CNN模型的精度更高,平均MAE比RF模型的降低了1.33%,RMSE则减少了2.46%。文献[12]等也证明了在解决某些回歸问题中,CNN模型性能优于RF模型。 基于变量角度,经变量选择后的模型其平均MAE比未筛选变量的模型减少了2.49%,EMSE则减少了3.40%,这证明了变量选择有助于提升模型性能。变量优化剔除了冗余特征,避免噪声对重要变量的遮蔽,进而促进模型泛化[14]。 综合不同算法与变量设置情况,基于RF变量选择的CNN模型具有最高的预测精度,其MAE为3.46%,RMSE为4.08%,均小于其他预测方案,表明该方案在电力负荷预测过程中的有效性。 4 结 论 电力负荷预测对协变量具有一定依赖性,从海量数据中选取合适变量集是优化电力负荷预测的有效方法之一。RF算法洞察协变量与电力负荷之间的关系,通过随机抽样的方法计算袋外数据对模型性能的影响进而对变量的重要性进行打分,这一变量选择过程是无偏最优的,通过对输入变量筛选后能够简化电力负荷预测模型结构、提升训练速率和泛化能力。CNN回归模型能自动获取电力负荷与协变量之间的复杂关系,并实现特征提取与智能模拟。与RF算法相比,该深度学习技术的预测精度有一定改进,能更有效反映电力负荷时间变化。RF与CNN组合算法从变量输入与数值拟合两个阶段优化电力负荷预测,为进一步改进预测性能提供技术参考。 参考文献 [1] 徐尧强,方乐恒,赵冬华,等. 基于LSTM神经网络的用电量预测[J]. 贵州电力技术,2017,20(8):25-29. [2] 赵兵,王增平,纪维佳,等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术,2019,43(12):4370-4376. [3] 杨维全,朱元振,刘玉田. 基于卷积神经网络的暂态电压稳定快速评估[J]. 电力系统自动化,2019,43(22):46-52. [4] 刘宝英,杨仁刚. 基于PCA-LSSVM的电力系统负荷预测方法[C]// 输配电技术国际会议,2007. [5] 张冰,周步祥,石敏,等. 基于灰色关联分析与随机森林回归模型的短期负荷预测[J]. 水电能源科学,2017(4):203-207. [6] 黄青平,李玉娇,刘松,等. 基于模糊聚类与随机森林的短期负荷预测[J]. 电测与仪表,2017,54(23):41-46. [7] 吴潇雨,和敬涵,张沛,等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化,2015,39(12):50-55. [8] 李泓泽,郭森,李缓,等. 考虑经济发展趋势的中长期电力负荷SALSSVM预测[J]. 陕西电力,2013,41(4):57-60. [9] 陆宁,武本令,刘颖. 基于自适应粒子群优化的SVM模型在负荷预测中的应用[J]. 电力系统保护与控制,2011,39(15):43-46. [10] 冯迎春,庄燕飞,任庆帅,等. 基于贝叶斯神经网络的电网超载负荷预测模型优化[J]. 电气应用,2016(4):38-41. [11] BREIMAN L. Random forest[J]. Machine Learning,2001,45:5-32. [12] PYO J C,DUAN H,BAEK S,et al. A convolutional neural network regression for quantifying cyanobacteria using hyperspectral imagery[J]. Remote Sensing of Environment,2019,233:111350. [13] 邹品晶,姚建刚,孔维辉,等. 基于多变量时间序列反演自记忆模型的中长期电力负荷预测[J].电力系统及其自动化学报,2017,29(10):98-105. [14] 梁智,孙国强,卫志农,等. 基于变量选择与高斯过程回归的短期负荷预测[J]. 电力建设,2017,38(2):122-128.
