基于演化模式挖掘和代价敏感学习的交通拥堵指数预测①
2020-10-19张翔宇吕明琪
张翔宇 张 强 吕明琪*
(*中国科学院计算技术研究所 北京 100190)(**中国科学院大学 北京 100049)(***北京赛迪时代信息产业股份有限公司 北京 100048)(****浙江工业大学计算机学院 杭州 310014)
0 引 言
交通拥堵指数(traffic congestion index,TCI)是对道路交通拥堵程度进行量化评价的一种指标[1]。然而,相比于对当前交通拥堵指数进行实时监测,对未来交通拥堵指数进行准确预测具有更大的价值。如帮助司机更好地进行路线规划[2],帮助城市管理者更好地进行道路建设规划[3]。
交通拥堵指数预测是一种交通流预测(交通流包括车流量、平均车速、交通拥堵指数等)。传统交通流预测主要在考虑交通系统物理特性的基础上采用交通模拟的方法[4-6]。然而,交通模拟需要设置大量的参数,而这些参数在真实环境中往往无法获得,因此交通模拟通常无法大规模地应用到整个城市的道路网络。随着交通数据采集设备的广泛部署,目前主流的交通流预测工作均采用数据驱动的方法。数据驱动的交通流预测方法主要包括统计模型、机器学习模型、深度学习模型。其中,统计模型主要基于时间序列分析实现预测,代表性方法包括Kalman滤波[7]、ARIMA模型[8]等。然而,统计模型无法有效地处理非线性数据,通常在交通流预测上难以取得理想的效果。机器学习模型可有效学习到交通流数据和各类影响因素的非线性关系,因此可实现更准确的预测,代表性方法包括支持向量机模型[9]、贝叶斯模型[10]、K近邻模型[11]等。然而,机器学习模型的性能严重依赖于特征,而特征主要依赖领域知识人工设计。因此,在处理复杂关联和潜在因素时显得能力不足。近年来,深度学习模型也逐渐应用到交通流预测领域。深度学习模型可自动从复杂数据中提取有效特征,摆脱了对人工设计特征的依赖,代表性方法包括前馈神经网络[12]、深度信念网络[13]、自动编码机[14]等。由于交通流是一类时序数据,时间关联对预测性能具有十分显著的影响,因此循环神经网络(如LSTM、GRU)逐渐成为交通流预测的主流深度学习方法[15-17]。此外,由于不同的道路间存在复杂的空间关联,且这些空间关联发生在不能用欧式距离度量的道路网络中,因此少量较新的研究工作尝试采用图神经网络进行交通流预测[18,19]。
现有方法虽然在交通流预测方面取得了显著的进展,但这些方法普遍存在一个问题:这些方法在短期交通流预测任务上性能优异,但在长期交通流预测任务上表现不佳(这里的长期预测指预测若干天后的交通流情况)。这是由于虽然这些工作采用了各种各样的模型,但这些模型本质上都属于回归模型。回归模型擅长捕捉数据的潜在关联,但不擅长捕捉数据的演化趋势。
针对此问题,本研究提出了一种融合演化模式挖掘和代价敏感学习的交通拥堵指数预测方法。该方法工作流程如下:给定某条道路的历史交通拥堵指数数据,首先对历史交通拥堵指数数据进行离散化,并采用序列模式挖掘算法从中挖掘出交通拥堵指数的演化模式,在此基础上设计一个基于演化模式的交通拥堵指数预测器。之所以对历史交通拥堵指数数据进行离散化,是由于演化模式是由离散型数据构成的。然后,从多个角度对影响交通拥堵指数的时空特征(如路网特征、区域特征、时序特征)进行提取,在此基础上建立基于机器学习的交通拥堵指数预测器。一方面,为与基于演化模式的交通拥堵指数预测器进行融合,基于机器学习的交通拥堵指数预测器的输出也应为离散型数据,因此采用分类模型构造预测器;另一方面,由于离散化后的交通拥堵指数数据间仍存在量化比较关系,而普通分类模型无法表示类型间的量化比较关系,因此采用代价敏感学习训练预测器。最后,基于Stacking技术对2个预测器的预测结果进行融合。
1 方 法
1.1 方法总体框架
定义1(交通拥堵指数)交通拥堵指数是一种用于对道路交通拥堵程度进行量化评价的指标。原始交通拥堵指数通常是连续型数据,数值越大代表拥堵程度越高。根据《城市道路交通拥堵评价指标体系》[20],将原始交通拥堵指数离散化为5个级别,交通拥堵指数离散值1~5分别代表非常畅通、畅通、轻度拥堵、中度拥堵和严重拥堵。因此,一个交通拥堵指数数据可表示为一个三元组tci=(d,r,t),其中d为交通拥堵指数离散值,r为待监测道路,t为采样时间。
图1展示了本文方法的总体框架,由演化模式预测器、机器学习预测器和融合器3个模块构成。其中,由于序列模式被现有研究证实可较好地捕捉时序数据的长期演化规律[21],演化模式预测器采用序列模式挖掘算法挖掘历史交通拥堵指数的演化模式,在此基础上基于演化模式匹配实现交通拥堵指数预测。机器学习预测器基于一系列的时空特征(如道路特征、区域特征、时序特征),采用代价敏感学习技术建立预测模型。融合器基于Stacking技术对演化模式预测器和机器学习预测器的输出进行动态融合,得到最终的预测结果。
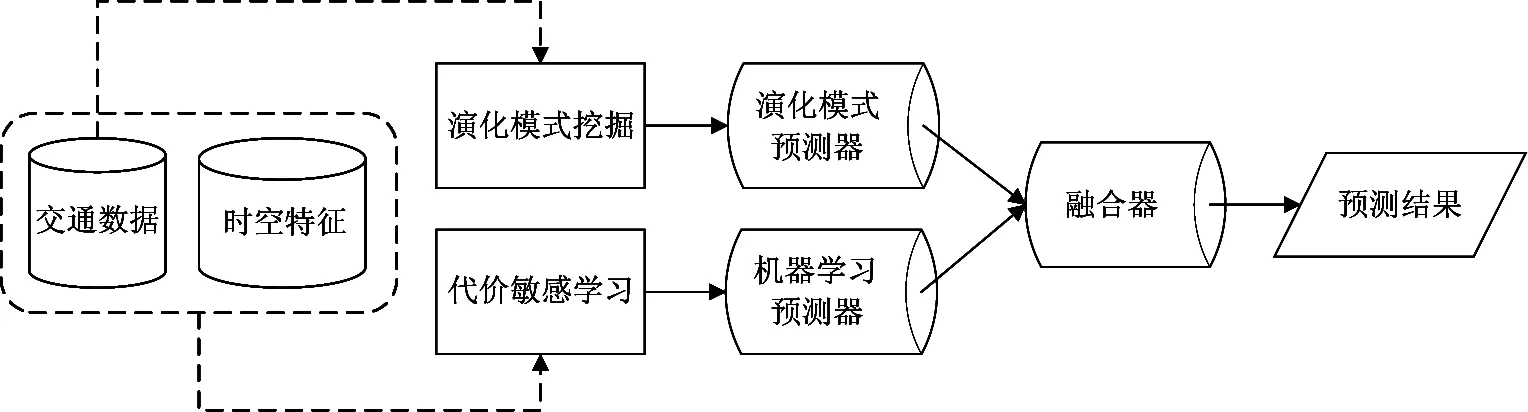
图1 本文方法的总体框架
1.2 演化模式预测器
交通拥堵指数在一定时间范围内通常存在特定的演化模式,演化模式预测器的构建方法如下。
第1步,为挖掘交通拥堵指数离散值的演化模式,扩展PrefixSpan算法[22],提出了一种基于数据投影的演化模式挖掘算法(投影的定义如下)。该算法的主要思路与PrefixSpan算法类似,给定一个序列集,首先根据当前前缀(频繁元素)去分割每一个序列,形成子序列集(当前前缀和分割得到的子序列集即为投影)。然后再递归地在子序列集上重复上述操作,使得前缀不断增长,形成演化模式。该思路的主要优势在于利用序列中元素的顺序信息逐渐减少搜索空间以提高算法效率。而提出的算法与PrefixSpan算法不同之处是在子序列集上搜索频繁元素扩展现有前缀时,仅在每个子序列的头部范围内进行搜索,一方面保证演化模式元素在原始序列中的相对连续性,另一方面进一步减少搜索空间、提高算法效率。如图2所示,给定历史交通拥堵指数离散值序列AS,算法首先通过序列分割为每个交通拥堵指数离散值ci构造一个投影(第1~3行)。然后,算法调用函数ExpandProjections递归地在现有投影基础上生成更多的投影。

图2 交通拥堵指数演化模式挖掘算法伪代码
定义2(投影)投影P可表示为一个二元组P=(PRP,SSP)。其中,PRP为该投影的前缀,可用于代表演化模式;SSP为一个AS的子序列集。
图3显示了ExpandProjections的工作流程:(1)在当前投影P的子序列集中搜索所有的频繁交通拥堵指数离散值(第1行)。(2)为每个频繁交通拥堵指数离散值cj构建一个新的投影NP(第2~3行)。其中,NP的前缀为连接P的前缀和cj得到,NP的子序列集为对每个头部范围内存在元素cj的P的子序列进行截断得到(第4~8行)。之所以仅在子序列的头部范围内搜索元素cj,是为了保证前缀中相邻的元素在历史交通拥堵指数离散值序列中的间隔也不是太大,以保证其相对连续性。(3)函数被不断地递归调用,直到新生成的投影包含的子序列集大小小于min_sup(第9~11行)。最后,当算法终止,可得到一个生成的投影集PS。对PS中每个投影P,PRP可被认为是一个演化模式,而SSP的大小可被认为是该演化模式的支持度。

图3 ExpandProjections函数伪代码
ExpandProjections每次执行过程中,频繁元素搜索步骤(第1行)的时间复杂度为O(|Y|×|SSp|),投影生成步骤(第2~8行)的时间复杂度为O(|Y|×|SSp|×head_range),因此函数一次执行的时间复杂度为O(|Y|×|SSp|×head_range)。由于ExpandProjections是一个递归函数,其每次执行都会缩短投影子序列的长度,直至无法搜索到频繁元素,因此最坏的情况下ExpandProjections会被执行|Y||AS|次,而在该情况下整个算法的时间复杂度为O(|SSp|×|Y||AS|×head_range)。此外,head_range对算法实际的计算复杂度影响巨大,这是由于增大head_range不仅会增加迭代次数,更重要的是会扩大头部搜索范围,使得搜索到目标交通拥堵指数离散值的概率大大增加,导致新投影的子序列数量难以快速减少,从而算法的递归次数更接近最坏情况。
第2步,基于挖掘得到的演化模式构造演化模式预测器。其核心思想是假定数据的演化过程遵循固定的一些模式,则当数据某次观测到的演化过程与某个模式的前部匹配时,将模式的后部作为本次的预测结果。该思路的核心步骤为演化模式匹配,即搜索前缀能够匹配交通拥堵指数当前观测到的演化过程的演化模式。本文基于树对演化模式进行索引(将该树称为演化模式树),其每个节点对应一个交通拥堵指数离散值及相应演化模式的支持度(根节点除外)。演化模式树构造方法如下:扫描所有演化模式,对每一个演化模式,采用深度优先搜索算法在演化模式树中搜索与该演化模式某个前缀完全匹配的分枝,然后将该演化模式的后缀插入到该分枝中并更新分枝每个节点的支持度。否则,将该演化模式直接插入根节点作为一个新的分枝。
第3步,给定交通拥堵指数当前观测到的演化过程RAS(即最近若干个交通拥堵指数离散值的序列)和演化模式树PT。交通拥堵指数预测方法如下:首先,在PT中搜索前缀能够匹配RAS的演化模式。演化模式树索引结构在这里的优势在于所有演化模式都可以直接以根节点作为入口搜索得到,从而有效减少搜索时间。然而,某些情况下可能会无法搜索到匹配的演化模式。针对这种情况,通过缩短RAS(删除RAS的第一个元素)进行再搜索,直到RAS的长度被缩短为1(此时一定能够搜索到匹配的演化模式)。此外,计算模式匹配率MR,即最终能够搜索到匹配的演化模式的RAS长度与最初RAS长度的比例(MR将在2.1节用作构造机器学习预测器的特征)。然后,以搜索到的演化模式的匹配前缀的最后一个节点作为入口,进行深度优先搜索直到叶子节点,所经过的路径即为预测结果。深度优先搜索的每一步都优先搜索支持度最高的子节点,且可得到一个交通拥堵指数离散值的概率向量(概率向量每个元素为某个交通拥堵指数离散值子节点在这一步被搜索到的概率,计算为该子节点的支持度与可选的子节点支持度之和的比例)。在该预测算法中,由于演化模式的长度通常有限,RAS太长会导致频繁无法搜索到匹配的演化模式,因此将RAS长度限制为max_length。
1.3 机器学习预测器
演化模式能发现交通拥堵指数数据的长期演化规律,但却无法捕捉交通拥堵指数数据和各影响因素间的潜在非线性关联,而机器学习技术在这方面有显著的优势。机器学习技术能够有效工作的关键包括2个方面:一是定义能够有效表征影响因素的特征,二是构建有效的机器学习模型。
在特征定义方面,许多现有工作发现,当前交通流除了与历史交通流相关之外,还与某些外部因素相关,如道路结构、城市功能分区等[23]。因此,机器学习预测器使用的特征包括从历史交通流数据集中抽取的时序特征以及从道路网络和兴趣地点数据集中抽取的外部特征。给定一个交通拥堵指数样本D=(rk,d),rk为样本所在道路,d为样本当前日期,具体特征抽取方法如下。
(1)时序特征。由于本文预测日平均交通拥堵指数,因此时序特征为rk在d的前h天到d的日平均交通拥堵指数序列,记为Mk=
(2)时间特征。时间特征包括待预测天是星期几、是否是假期。时间特征向量记为Tk。
(3)道路特征。道路特征包括rk的道路类型(如高架路、主干路、次干路)、道路方向(如双行线、单行线)、交叉口数量、道路长度、道路扭曲度(即道路长度与道路端点直线距离的比例),rk的道路特征向量记为Rk。
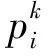
(1)
综上,Rk和Pk为静态特征,Mk和Tk为动态特征,则样本D的特征向量为
在模型构建方面,由于演化模式是离散的数据序列而演化模式预测器输出的也是交通拥堵指数离散值,因此本文基于分类模型建立交通拥堵指数的机器学习预测器,以便于后续演化模式预测器和机器学习预测器的融合。然而,直接采用标准的分类模型用于交通拥堵指数预测存在标准分类模型的训练目标为最大化准确率,并对所有分类错误同等对待。例如,对于一个真实交通拥堵指数离散值为2的样本,预测结果为3和5对于标准分类模型的分类错误损失是一样的。然而,在本问题中,预测结果为5相比预测结果为3更不能接受,即预测结果为5的分类错误损失应该更大。针对此问题,本文采用代价敏感学习技术训练分类模型。代价敏感学习的主要思想是通过定义不同分类错误的代价,使得分类错误代价大的样本在模型训练过程中造成更大的损失,从而最终的模型能够最小化总的分类错误代价。具体步骤如下。
首先,定义用于计算分类错误代价的代价矩阵C,使得预测误差越大分类错误代价越高。假定真实交通拥堵指数离散值为i,而预测交通拥堵指数离散值为j,则C为一个5 × 5的矩阵,分类错误代价为C[i,j]=|i-j|。然后,基于代价矩阵,采用代价敏感学习算法GLL-MCBoost[24]训练分类模型。除了能将分类错误代价反映到损失函数中,GLL-MCBoost算法还具有如下优势:其可以有效处理arbitrary guess样本,arbitrary guess样本指该样本在多个类型上的预测概率相同,这种情况下分类器只能给出一个随意猜测。GLL-MCBoost算法通过boosting机制在每轮迭代中增加arbitrary guess样本的权重,使其能在下一轮迭代中得到更有效的训练。
1.4 融合器
演化模式预测器和机器学习预测器的输出均可表示为一个5维向量,其中向量的第k个元素代表预测交通拥堵指数离散值为k的概率。由于这2个预测器采用完全不同的技术构建,它们具有不平衡的预测能力,甚至对不同样本预测能力的不平衡程度也不同。因此,简单对2个预测器的预测概率求平均无法取得理想的性能。针对此问题,采用Stacking技术对2个预测器的输出进行融合。其主要思想为融合多个子模型,将这多个子模型输出的预测结果作为新的特征,在此基础上再训练一个元模型。元模型可学习到不同子模型预测能力的不平衡性,并基于此给子模型输出的预测结果分配权重,这比简单对子模型输出的预测结果求平均效果更好。
给定训练样本集TS={S1,S2,…,SN}和交通拥堵指数离散值值域Y={1, 2, 3, 4, 5},Ppattern(Sk,y)和Pfeature(Sk,y)分别代表演化模式预测器和机器学习预测器预测样本Sk的交通拥堵指数离散值为y的概率。此外,采用2.1节中的模式匹配率MR(Sk)作为一个额外的特征(这是由于模式匹配率对演化模式预测器的预测性能有很大影响)。综上,可得到一个元特征向量MF={MR(S1),Ppattern(S1, 1),…,Ppattern(S1, 5),Pfeature(S1, 1),…,Pfeature(S1, 5)},…,MR(SN),Ppattern(SN, 1),…,Ppattern(SN, 5),Pfeature(SN, 1),…,Pfeature(SN, 5)}。在此基础上,训练一个将MF映射到Y的元预测器MP。最终,当对样本Sk进行实时预测时,首先分别采用演化模式预测器和机器学习预测器对其进行预测,得到元特征向量MFk={MR(Sk),Ppattern(Sk, 1),…,Ppattern(Sk, 5),Pfeature(Sk, 1),…,Pfeature(Sk, 5)}。然后,采用元预测器MP对MFk进行预测得到最终结果。
2 实 验
2.1 实验准备
为进行实验,从杭州市采集了如下真实数据集。
(1)交通拥堵指数数据集。从杭州市交通拥堵指数实时监测平台[25]上爬取了3年多的历史交通拥堵指数数据(从2014年8月至2017年12月)。该数据集包含199条道路(其中一条双向道路被认为是两条不同的道路)。原始交通拥堵指数每15分钟发布一次,为预测日平均交通拥堵指数,对每天的交通拥堵指数求平均,最终得到229 709个样本。
(2)道路网络数据集。该数据集包含交通拥堵指数数据集涉及的199条道路,其中道路平均长度为2.6 km,包括30条高架路、153条主干路、16条次干路。
(3)兴趣点数据集。该数据集包含从百度地图中采集的杭州市的39 305个兴趣点(每个兴趣点属于居住、工作、商业、宾馆、学校、交通、预测和景区的其中一个类型)。
实验采用10折交叉验证作为测试方案(即90%的数据作为训练集,10%的数据作为测试集,测试重复10次取平均性能)。实验采用如下2个指标进行性能评价,即准确率(ACC)和误差(ERR),计算方法如式(2)和式(3)所示。其中,pi和gi分别为测试样本Si的预测值和真实值,x为真则I(x)=1,x为假则I(x)=0,n为测试样本数量。
(2)
(3)
2.2 实验1演化模式预测器测试
第1个实验测试min_sup(演化模式最小支持度阈值)对预测性能的影响。首先,由于min_sup的值依赖于历史交通拥堵指数离散值序列的长度L(例如,若L较短,则应设置一个较小的min_sup,以避免挖掘不出演化模式的情况),导致其具体数值范围难以确定。因此,设置一个取值范围为(0, 1)的相对值min_sup_rate,并计算min_sup=min_sup_rate×L。然后,固定max_length=5,将min_sup_rate从0.05减少至0.0006以观察演化模式预测器性能的变化,结果如图4所示,其中“Day +k”指预测未来第k天的交通拥堵指数。可以看出,当min_sup_rate从0.05减少至0.01时,ACC明显上升,而当继续减少min_sup_rate时,ACC的上升趋势趋于稳定,ERR的变化趋势与此类似。这是由于min_sup_rate较大时,则演化模式挖掘算法对演化模式的要求更为严格,因此挖掘出的演化模式数量更少、长度更短,导致演化模式预测器的能力减弱。然而,将min_sup_rate设置的过小会极大地增加计算复杂度,且容易引入更多的噪声[26]。综上,将min_sup_rate设置为0.002。
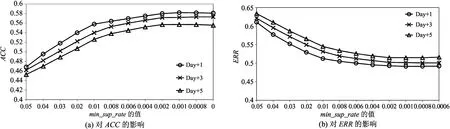
图4 参数min_sup_rate对演化模式预测器性能的影响
第2个实验测试max_length(当前演化趋势长度)对预测性能的影响。首先,固定min_sup_rate=0.002,将max_length从1增加至10以观察演化模式预测器性能的变化。如图6所示,当max_length增加时,ACC的变化趋势是先明显上升,再趋于稳定(甚至有少量下降),ERR的变化趋势与此类似。这说明演化模式预测器的有效工作依赖于一定长度的当前演化趋势。然而,由于挖掘出的演化模式长度通常有限,max_length长度过长通常会引入过多无用甚至是噪声的元素,导致模式匹配失败。综上,将max_length设置为7。
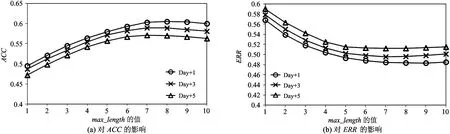
图6 参数max_length对演化模式预测器性能的影响
第3个实验测试演化模式挖掘算法的计算复杂度。根据第2.2节的讨论,参数head_range对算法的计算复杂度影响巨大,因此本实验探索在不同head_range取值的情况下演化模式挖掘算法的运行耗时。算法的输入为一条道路的所有历史交通拥堵指数数据序列(长度约为106 560),min_sup_rate设置为0.002,实验采用的计算机配置为Intel双核CPU(2.70 GHz × 2)、16GB内存,程序采用Java语言编写。实验结果如图7所示,可以看出随着head_range的增大,算法运行耗时急剧增加。此外,head_range设置的过大会破坏演化模式中元素在原始序列中的连续性。后续实验中将head_range设置为1。
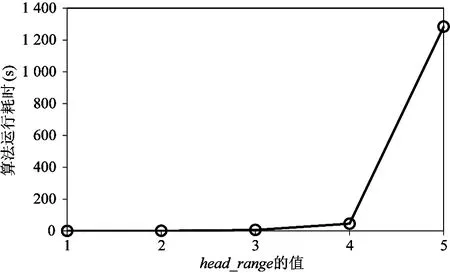
图7 head_range参数对演化模式挖掘算法运行耗时的影响
2.3 实验2机器学习预测器测试
第1个实验测试参数h(时序特征中考虑前几天的数据)对预测性能的影响并确定参数取值。如图8所示,当h增大时,ACC逐渐上升而ERR逐渐降低,特别是h取值较小的时候。这说明过去几天的交通拥堵指数可有效用于对未来的交通拥堵指数的预测。然而,h增大到一定程度之后无法持续改善预测性能。综上,将h设置为6。
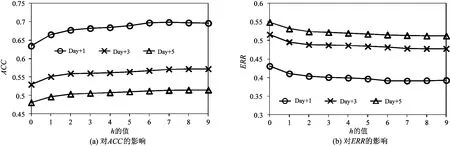
图8 参数h对机器学习预测器性能的影响
第2个实验验证静态特征、动态特征以及代价敏感学习机制的有效性。图9比较了3种方法的预测性能,即Dynamic(仅使用动态特征,基于代价敏感学习机制构建机器学习预测器)、Dynamic + Static(使用所有特征,基于代价敏感学习机制构建机器学习预测器)和RF(使用非代价敏感学习机制构建机器学习预测器,这里所有特征都被使用,分类模型采用随机森林)。首先,Dynamic + Static的性能始终优于Dynamic。这说明静态特征对交通拥堵指数预测任务是有效的。其次,与RF相比,Dynamic + Static的ACC较低,但ERR较高。这说明代价敏感学习机制不能减少被错误预测的测试样本的数量(甚至会增加),但可以有效减少被错误预测的测试样本造成的总体损失。
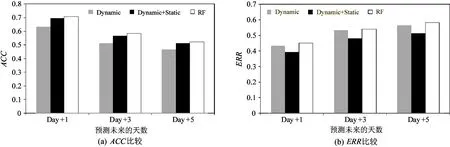
图9 不同方法设置的性能比较
2.4 实验3比较实验
将本文提出的方法(称为OUR)与如下3个方法进行比较:(1)PATTERN,即演化模式预测器;(2)FEATURE,即机器学习预测器;(3)LSTM,采用深度学习模型LSTM构建交通拥堵指数预测模型[16]。实验结果如图10所示,从图中可以得出如下结论。
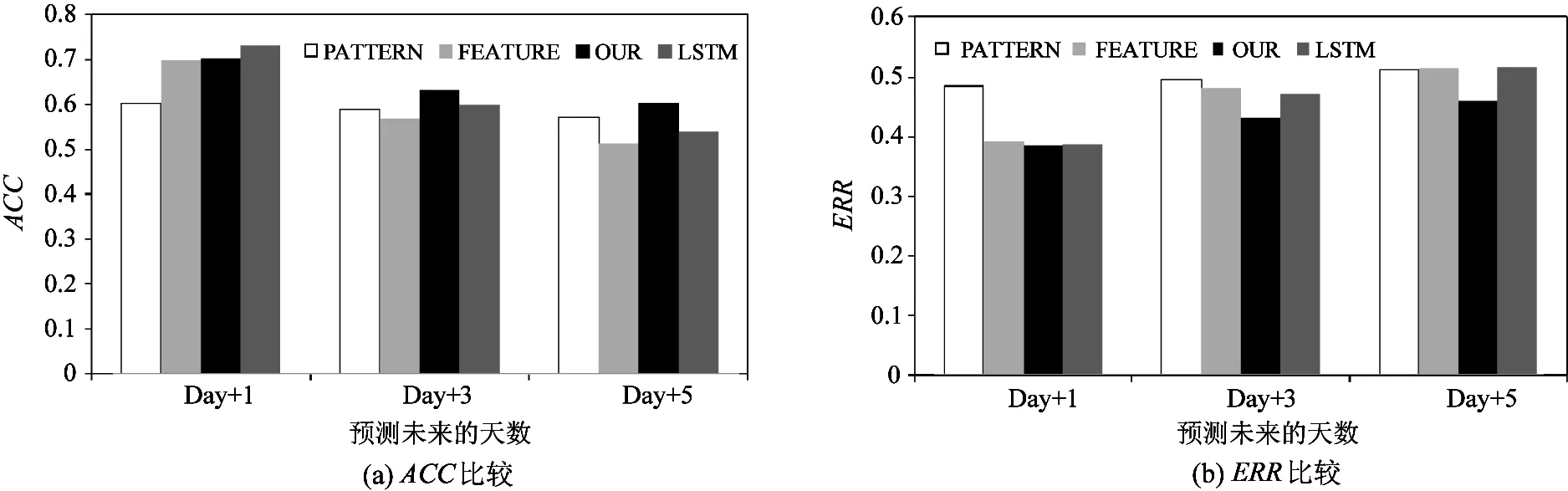
图10 不同方法的性能比较
(1)当预测较近的未来交通拥堵指数时(如Day +1),FEATURE相比于PATTERN具有较为明显的优势,而PATTERN的优势在预测较远的未来交通拥堵指数时逐渐显示出来。这说明演化模式可较好地捕捉长期的交通拥堵指数变化规律。(2)LSTM在ACC上始终优于FEATURE,这说明深度学习模型的学习能力比传统机器学习模型更强。然而,LSTM和FEATURE在ERR上的表现差别不大,这说明代价敏感学习机制可更有效地减少预测误差。(3)相比PATTERN和FEATURE,OUR的总体性能更优。这说明融合器能有效地利用演化模式预测器和机器学习预测器各自的优势,从而得到更准确的预测结果。(4)LSTM在预测较近的未来交通拥堵指数时的性能比OUR要好,但OUR在预测较远的未来交通拥堵指数上表现更好。因此,在实用中,OUR和LSTM可作为互补的方法,即采用LSTM对短期交通拥堵指数进行细粒度预测,采用OUR对长期交通拥堵指数进行粗粒度预测。
3 结 论
本文提出了一种融合演化模式和机器学习的交通拥堵指数预测方法。其中,演化模式预测器通过挖掘能够捕捉交通拥堵指数长期变化规律的演化模式实现预测,机器学习预测器通过学习交通拥堵指数与一系列交通特征的关联实现预测。基于真实数据的实验发现,本文提出的方法一方面在预测粗粒度长期交通拥堵指数任务上具有优势,另一方面能够有效降低预测的总体损失。
