焊接结构裂纹扩展分析的无网格和水平集耦合方法

刘 晖，申韶丁，雷 电

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

0 引 言

焊接结构是工程中应用非常广泛的结构形式之一，焊接结构在焊接过程中不可避免地会存在初始裂纹缺陷，具有焊接初始裂纹缺陷的构件或结构疲劳裂纹扩展非常迅速，进而引起结构破坏[1]。因此，研究焊接结构存在初始裂纹扩展行为，对预防焊接结构破坏，保证结构使用安全具有重要意义。

对于裂纹扩展模拟分析，许多学者做了大量的研究，取得了一定的成果，并提出了很多模拟裂纹扩展的方法[2-5]，其中有限元法是目前运用最为广泛并且发展最为迅速的数值计算方法[6-7]。解德等[8]采用ABAQUS有限元分析软件实现了基于有限元的模拟裂缝扩展方法。李长安[9]将基于有限元的虚拟裂纹闭合法(VCCT)应用于疲劳裂纹寿命预测，并降低了网格敏感性，使得在粗糙网格下也能获得比较精确的结果。刘艳萍等[10]基于VCCT法，采用Zigzag模型近似模拟裂纹前沿，分析了具有不同裂纹形式的简单几何体，获得了比较理想的结果。由于有限元法及其衍生方法是一种基于网格的方法，在划分单元时要防止单元畸变或缠结现象，当结构出现裂纹扩展时，网格会发生扭曲甚至畸变，裂纹扩展的每一步都要重新划分网格，这要花费大量的前处理时间。模拟平面问题中任意放置的直线裂纹和弯曲裂纹的弯折扩展时，单元网格会产生过度扭曲，或造成计算中断，不能真正跟踪裂纹扩展路径。

无网格法作为一种新兴的数值计算方法，将求解域基于节点离散，无需划分单元，并且在裂纹扩展时仅需局部和少量人为介入[11-13]。

袁振等[14]提出将无网格伽辽金法用于复合型裂纹的扩展模拟并估算其疲劳寿命。陈建等[15]通过无网格伽辽金法对含边沿裂纹功能梯度材料板进行应力强度因子的计算。传统无网格法处理不连续问题时，对裂纹几何形状难以描述，用透视法等一些方法处理裂纹隔离作用时，人为增加了不连续性，计算过程复杂，不易推广到三维问题上。

本文提出采用无网格和水平集耦合法来对焊接结构存在初始裂纹几何形状进行描述，并模拟裂纹扩展。水平集法是一种追踪界面移动的数值模拟方法[16]，也是基于节点离散的方法，因此两者可以很自然地实现耦合，水平集法采用2个相互正交的水平集函数对裂纹几何形状进行描述及裂尖位置进行定位。在无网格法的近似函数中增加了裂尖处的Westergard扩展项和跳跃函数Heaviside[17]，使计算点不受裂纹隔离影响，裂纹扩展时只需更新水平集函数，避免了无网格法计算每一步裂纹扩展时都需要在裂尖位置进行节点加密和人为增加的不连续项，保证了刚度矩阵的带状和稀疏，并且节点划分只在裂尖部分的带状区域，既保证了计算精度又提高了计算效率。最后，本文以焊接节点为环状形式截面且存在初始焊接裂纹为研究对象，编制了基于极坐标的无网格和水平集耦合法程序，分析其裂纹扩展，并跟踪了裂纹扩展路径。

1 焊接结构裂纹扩展分析理论及流程

1.1 裂纹扩展判别依据

最大周向拉应力强度因子理论是判断复合型裂纹断裂应用最为广泛的准则，该理论计算应力强度因子简单，易于实现，被广泛应用于工程中，故本文采用此准则作为裂纹扩展判别依据。裂纹扩展角θc应满足

KⅠsin(θc)+KⅡ[3cos(θc)-1]=0

(1)

式中：KⅠ，KⅡ分别为Ⅰ型和Ⅱ型裂纹的应力强度因子(SIF)。

求解式(1)可得

(2)

式中：sign(·)为符号函数。

根据线弹性力学理论，裂纹尖端的应力通常是趋近于无穷大的，不能作为判断裂纹失效的准则，因此采用应力强度因子的概念来反映裂尖奇异应力场的强弱。

复合型裂纹尖端附近极坐标应力场θ方向分量表达式为

(3)

当θ=θc时

(4)

式中：r,θ为以裂纹尖为坐标原点的极坐标系；Kθmax为最大周向拉应力强度因子，当Kθmax大于材料断裂韧度KIC时，裂纹开始扩展。

1.2 裂纹扩展分析步骤及流程

裂尖处的SIF大小表示裂尖处应力场的强弱，模拟裂纹扩展就是计算裂尖处的SIF。因此，本文通过以下步骤计算SIF，最终实现对焊接节点的裂纹扩展路径跟踪。

步骤1：采用无网格Garlerkin法(EFGM)和水平集法耦合建立模型，将模型求解域基于节点离散，通过计算节点水平集函数将节点划分为常规节点、阶跃扩展节点和裂尖扩展节点。

水平集函数Ψ(x,t)采用符号距离函数表示

(5)

式中：x，t分别为计算点的坐标向量和时间变量；Γc为裂纹面；xΓ为位于Γc上的计算点。

如果计算点x位于Γc的上方，则水平集函数Ψ(x，t)为正，否则为负。

移动界面Ψ(x，t)的演化方程为

Ψt+F‖Ψ‖=0

(6)

式中：Ψt为t时刻的界面；F为界面上点x∈Γc(t)在界面外法线方向的移动速度向量；为梯度算子。

初始裂纹波前水平集函数为

(7)

水平集法通常采用裂纹面水平集函数和波前水平集函数描述裂纹位置及形状，裂纹面水平集函数Ψ(x,t)=0表示裂纹及其延长部分，初始裂纹由Ψ(x,t)=0和波前水平集函数φ≤0确定，那么裂纹面通过计算上述2个函数就可对节点进行划分，阶跃扩展节点集合M的表达式为

M={n∈Q∶φ<0且Ψ-rd≤0}

(8)

式中：rd为节点影响域半径；Q为求解区域内离散的节点集合；n为任意节点。

裂尖扩展节点集合K的表达式为

(9)

当节点既为阶跃扩展节点又为裂尖扩展节点时，优先按裂尖扩展节点处理。

步骤2：根据EFGM和水平集耦合法推导整体刚度矩阵、荷载和位移向量，求解节点的应力场和位移场。

根据线弹性断裂力学的Westergaard解及EFGM的单位分解特性，耦合法的不连续位移场函数uI(x,t)可表示为

(10)

(11)

(12)

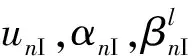
无网格和水平集耦合法的离散方程为

(13)

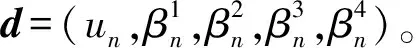
整体刚度矩阵的元素kij表达式为

(14)

式(14)上标表示对应的节点自由度，具体形式表达为

(15)

式中：B为应变矩阵；D为弹性矩阵；Ω为计算域。

边界项刚度矩阵的元素gij表达式为

(16)

荷载向量f中元素表达式为

(17)

式(17)上标表示对应的节点自由度，具体形式为

(18)

(19)

(20)

步骤3：根据式(13)计算得到节点的位移场，进而得到应力场，然后采用相互作用积分法[18]计算裂纹尖端区域的SIF。通过最大周向应力准则确定开裂步长，计算裂纹开裂角。

步骤4：当裂纹在荷载作用下扩展时，通过水平集更新算法对节点水平集函数进行更新[19]，从而对裂纹几何形状和裂尖位置进行追踪，实现对裂纹扩展路径的精确模拟。

以二维问题为例来说明具体的实现步骤：

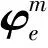
(21)

Ψm+1=±|(x-xi)(F/‖F‖)|=±|(x-xi)|·

(Fy/‖F‖)+(y-yi)|(Fx/‖F‖)|

(22)

式中：正负号表示裂纹两侧更新部分的符号与未更新部分的符号保持一致。

(23)

式中：Δαm为第m步的扩展步长或者增量。

2 数值算例

为了验证本文方法的适用性和程序设计的正确性，选取应力强度因子手册中经典边缘受拉裂纹算例进行计算。板模型如图1所示，平板宽度L=1 m，高度D=2 m，板的上表面承受均匀拉应力σ=1 MPa，板的左侧中间部分有一边缘裂纹长度a=0.45 m，弹性模量E=1×103Pa，泊松比ν=0.3，应力强度因子的精确解为

图1 边缘受拉裂纹模型

(24)

采用本文方法，首先将求解域离散为12×24个均匀布置的节点，则背景网格分布为11×23，每个背景网格内设置6×6的高斯积分点，基函数选用二次基函数P=[1,x,y]T，权函数选用3次样条权函数，影响域半径选为1.7倍的最大相邻节点间距rd，采用水平基函数将节点划分为阶跃扩展节点和裂尖扩展节点，节点分布如图2所示。

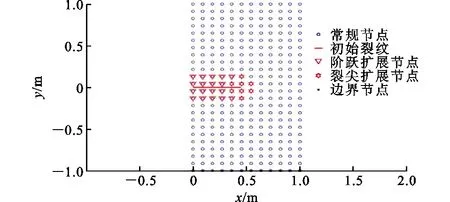
图2 节点分布

节点变形如图3所示，为绕裂尖位置发生受拉变形。模型应力云图如图4所示，在裂尖位置应力最大，随着远离裂尖位置应力逐渐减小。采用本文方法计算结果与解析解对比如图5所示，本文解与解析解基本一致，说明本文方法具有较高精度，验证了本文方法的可行性和程序设计的正确性。

图3 节点变形

图4 应力云图(单位:MPa)

图5 不同裂纹长度对应的SIF

焊接节点的一种形式是管球焊接节点或钢管对焊节点，因此，本文以焊接结构存在初始裂纹、具有环状横截面为研究对象分析其裂纹扩展行为。基于极坐标系建立了如图6所示的模型，材料为Q345钢材，弹性模量E=2.06×1011Pa，泊松比ν=0.3，焊缝标准为二级焊缝，在外边界上受切向均布荷载P=40 N。裂纹线为水平方向位置从A点(30，π)到B点(25，π)，裂纹长度a=5 mm，裂尖坐标为(25，π)。

图6 焊接节点模型示意

采用均匀布点法在求解域内进行离散，外环半径R为30 mm，内环半径r为20 mm，径向方向等间距布置8个节点，弧度方向为每隔π/36等弧度布置72个节点。

影响域半径过小，裂纹线附近的阶跃扩展节点不能完全覆盖裂纹区域，对裂纹描述不够精确；影响域半径过大，裂尖扩展节点过多，放大了裂尖区域的奇异性。因此，通过对比分析，本文选取2.2倍节点间距rd作为影响域半径，裂尖部分的奇异场能够得到足够的节点位移近似函数加强，同时裂纹线附近的阶跃扩展节点也能够完全覆盖裂纹区域，使得计算点影响域不受裂纹隔离的影响，如图7所示。

图7 在2.2rd下的节点划分

根据式(13)计算得到应力场和位移场以后，采用相互作用积分法计算应力强度因子，本文选取每一步裂纹扩展增量da为a/5，da过大不适用于线弹性断裂力学，会导致计算结果不精确；da过小，模拟裂纹扩展时计算量大，并且计算所得SIF和θc不具有代表性。通过水平集更新算法更新裂尖位置及水平集函数，从而实现对裂纹扩展的追踪，得到最终的每一步扩展增量下裂尖处的应力强度因子，如图7所示。所得裂纹扩展角如表1所示，应力强度因子随裂纹扩展增量的变化如图8所示，裂纹扩展路径如图9所示。

表1 裂纹扩展对应的SIF及扩展角

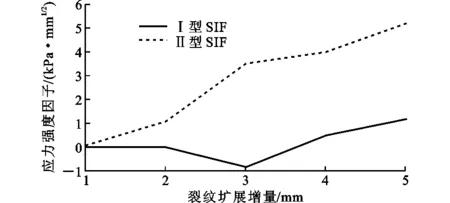
图8 SIF随裂纹扩展增量的变化

图9 裂纹扩展路径

3 结 语

(1)本文方法避免了单纯的无网格法处理不连续问题时所增加的人为不连续项，能够组装成具有带状、稀疏性的整体刚度矩阵；对于裂纹扩展区域加强点选取仅限制在裂纹附近的带状区域内，简化了加强点选取和附加函数的建立，不会过多增加整体自由度，并且无需求解水平集更新算法的演化方程，因此计算过程简单，易于在程序上实现，提高了计算效率。

(2)本文方法的计算精度较高，结果光滑协调，且能很好地跟踪裂纹扩展路径，能够预测焊接结构存在初始裂纹的裂纹扩展及走向。

(3)本文方法计算量小、精度高，可以实现裂纹路径跟踪，易于推广到三维节点模型，为预测复杂工程结构在复杂荷载下的断裂行为提供了一种可靠的计算途径和模拟思路。