不同圆心角圆端形钢管混凝土短柱轴压性能
2020-10-19任志刚王丹丹
任志刚,王丹丹
(武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)
0 引 言
钢管混凝土柱具有承载力高、塑性韧性较好和施工方便等优点,广泛应用于建筑和桥梁工程中,许多学者对其展开研究[1-6]。圆端形钢管混凝土柱以外部圆端形钢管为框架,内部浇筑混凝土而成,具有与钢管混凝土相同的优势。此外,其造型较为美观,可兼顾较好约束效应所展现的较强承载能力和较大截面惯性矩所带来的较优压弯性能,适用于受弯能力不同的压弯构件中。
对圆端形钢管混凝土短柱的研究方法主要有试验与有限元分析2种方式。王志滨等[7-9]对圆端形钢管混凝土构件进行轴压试验,研究不同截面高宽比、含钢率以及构造措施下的试件破坏形态与力学性能。Hassanein等[10-11]采用ABAQUS软件对试验构件进行模拟并进行参数分析,模拟结果与试验结果吻合良好。谢建雄等[12-13]对圆端形钢管混凝土双肢塔柱及其变截面进行有限元分析,讨论外钢管对核心混凝土的约束效应。
目前针对圆端形钢管混凝土短柱力学性能的研究主要集中于两端半圆形与中间为矩形的截面形式,对圆心角θ(0°<θ<180°)的圆端形构件研究尚未见报道,为研究圆心角改变时圆端形钢管混凝土短柱力学性能变化,对2个圆心角分别为60°和120°的圆端形钢管混凝土短柱进行试验研究和有限元分析。采用通用有限元软件ABAQUS对试验结果进行验证及参数分析,并根据试验结果与参数分析结果,分别建立圆心角为60°和120°的圆端形钢管混凝土轴压短柱极限承载力计算公式。
1 试验研究
1.1 试验概况
圆心角为60°和120°的圆端形钢管混凝土横截面形式如图1所示,其中D为横截面宽度,H为横截面高度,B为中部矩形高度。共设计4个试件,试件编号、实测尺寸及基本性能如表1所示。表1中试件编号RCC代表圆端形钢管混凝土,t为钢管壁厚,L为试件高度,ξ为试件约束效应系数。圆端形钢管采用热轧钢板加工对焊成型,其强度如表2所示。混凝土配合比为:水180.0 kg·m-3、水泥420.0 kg·m-3、砂320.0 kg·m-3和骨料1 161.1 kg·m-3。混凝土立方体抗压强度设计值为30 MPa,立方体抗压强度实测值为31 MPa。

图1 圆端形钢管混凝土截面形式
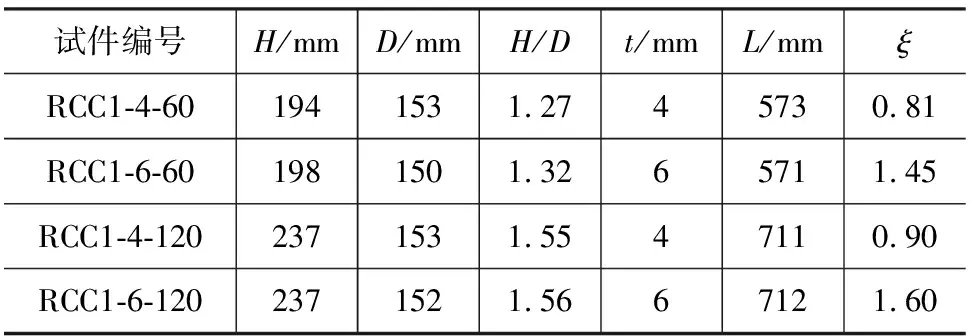
表1 试件参数

表2 钢材材性
圆端形钢管加工成型后底端焊接10 mm厚盖板,在其外表面涂油漆防止锈蚀,同时画50 mm×50 mm网格。从未焊盖板一端灌入混凝土,并用振捣棒振捣,防止混凝土内部有气泡产生,同时制作边长为150 mm的标准立方体试块,与圆端形钢管混凝土试件同条件养护。待混凝土凝结硬化后,打磨机打磨平整并补涂环氧砂浆使之与钢管端部截面齐平,最后焊接10 mm厚盖板,保证其在受荷初期共同受力。
1.2 试验方法
圆端形钢管混凝土轴压试验采用500 t压力试验机,每个试件钢管中部横截面6个位置分别布置横向和纵向应变片,其位置对应于图2中A1,A2和A3。试件加载与测试装置如图2(a)所示。在弹性阶段试件采用连续加载模型,当荷载为预测荷载70%时转为分级加载模式,每级荷载加载时间为3~5 min,并采集1次数据,试件接近极限荷载及破坏后连续采集数据。

图2 试验装置
2 试验现象和结果分析
2.1 试验现象
在加载初期试件基本上表现为弹性,当荷载增加至极限荷载的60%~70%时,试件进入弹塑性工作状态,并且没有明显屈曲现象,但荷载-轴向应变曲线表现出非线性特征。随着轴向应变增加,当荷载达到极限荷载时,圆端形钢管内部混凝土向外鼓曲,圆心角为60°的圆端形钢管混凝土试件的破坏形态与方形钢管类似,平直段与圆弧段均出现明显外部鼓曲现象,与矩形试件相比,其外钢管屈曲发生较晚,圆弧段屈曲的程度与矩形试件相比幅度较小。圆心角为120°的试件屈曲现象只发生于平直段,表明圆心角为120°的短柱圆弧段约束效应较好,其破坏形态如图3所示;随着试件变形逐渐增大,试件承载力下降或维持平稳状态,最后因变形过大,焊缝开裂而终止试验。

图3 试件破坏形态
2.2 荷载-轴向应变曲线
图4为试件荷载-轴向应变(N-εL)曲线。由图4可见,所有试件的N-εL曲线在峰值荷载处均有一段相对平稳的线段,表明试件均表现出良好的塑性变形能力。这是因为试件的H/D≤1.56,外部钢管对核心混凝土具有较强的约束效应。对于钢管厚度为6 mm的试件,在试件达到极限荷载时,仍具有较强的承载性能,荷载-应变(N-ε)曲线没有明显的下降段。

图4 荷载-轴向应变曲线
2.3 强度指标
为对不同圆心角试件的承载力进行比较,采用强度指标SI进行分析,其计算公式为
SI=Nuo/(fcAc+fyAs)
(1)
式中:Nuo为试验实测极限承载力;fc,fy分别为混凝土计算轴心抗压强度和实测钢材屈服强度,且fc=0.76fcu,fcu为混凝土轴心抗压强度;Ac,As分别为混凝土和钢管横截面面积。
试件的极限承载力与强度指标如表3所示,其强度指标均大于1,表明与钢管和混凝土简单叠加相比,组合后的承载力较大。图5(a)为圆心角不同时强度指标的变化趋势,结果表明:对于截面宽度为150 mm的试件,当截面圆心角由60°增大到120°时,SI值分别下降了16.7%和9.3%(分别对应钢管厚度为4 mm和6 mm)。其原因为:随着圆心角增大,试件高宽比增大,整体约束效应减弱。

表3 极限承载力对比

图5 SI变化
图5(b)为截面宽厚比对强度指标SI的影响,结果表明,随着试件宽厚比减小,SI值明显增大。这是因为钢管厚度越大,宽厚比越低,外钢管对核心混凝土约束效应越强,当试件厚度由4 mm增大到6 mm时,圆心角为60°和圆心角为120°的试件SI值分别增大了6.0%和15.5%,表明圆心角为120°的试件钢管厚度对极限承载力提高效果优于圆心角为60°的圆端形钢管混凝土试件。
2.4 约束效应分析
为讨论圆心角为60°和120°时对试件约束效应的影响,对不同圆心角试件中部横截面圆弧段中点A3进行轴向应力-轴向应变(σ-εL)和环向应力-轴向应变曲线分析,如图6(a)所示。结果表明,随着圆心角的增大,A3处钢管环向应力逐渐增大,轴向应力与环向应力之间的差距逐渐减小,表明约束效应逐渐增大,且圆心角为120°的试件环向应力较圆心角为60°的试件强,表明圆弧段处约束效应较强。图6(b)为试件RCC1-4-60中截面A1,A2,A3处的轴向应力和环向应力曲线,结果表明,与中截面A1,A2处相比,A3处外包钢管对核心混凝土在弹性阶段的约束效应较小,随着应变增大,A3处约束效应逐渐增大,且A3处环向应力值大于A2和A1处的环向应力值,这是因为A3为圆弧段,当轴向应变从峰值应变逐渐增大时,环向约束效应开始发挥作用。
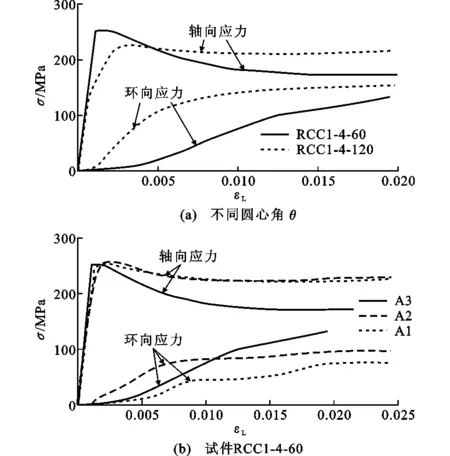
图6 应力-轴向应变曲线对比
2.5 荷载-应变曲线
图7为试件RCC1-4-60与RCC1-4-120中截面平直段A1处荷载-应变(N-ε)关系曲线,其中εl为纵向应变,εt为环向应变,εy为钢材屈服应变。结果表明:当圆心角为60°时,外钢管纵向首先达到屈服强度,随后环向达到屈服强度;当圆弧段圆心角增大为120°时,环向中截面平直段处外钢管纵向与环向几乎同时达到屈服强度。

图7 A1处荷载-应变曲线
3 有限元分析
3.1 模型建立
采用有限元软件ABAQUS进行建模,钢管选用4节点壳单元(S4R),沿厚度方向9节点Simpson积分,混凝土与盖板为8节点实体单元(C3D8R),采用减缩积分模式。网格划分采用结构化网格,如图8所示。钢管与混凝土采用面与面接触,法向方向为硬接触,切线方向为库仑摩擦,摩擦因数为0.6。钢管与加载板的接触形式为壳-实体耦合,混凝土与加载板的接触形式为绑定约束。此外采用位移加载模式,并在与两端板中心沿距离20 mm左右各设置一参考点,参考点与端板采用耦合约束形式。
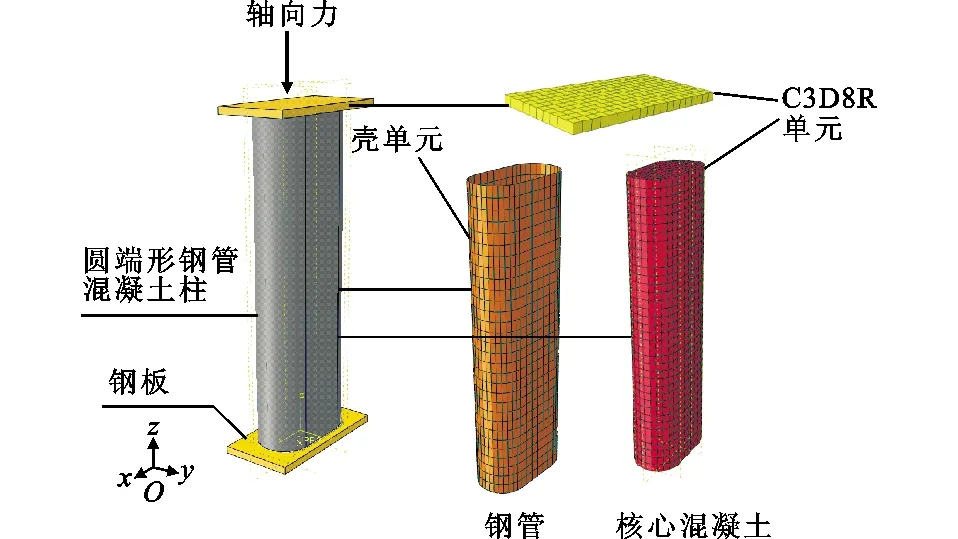
图8 圆端形钢管混凝土有限元模型
圆端形钢管混凝土短柱为全截面形式建模,采用位移加载模型和牛顿-莱布尼茨(Newton-Leibniz)公式进行非线性方程组求解。
混凝土受压应力-应变关系曲线及相应参数的取值见文献[9]~[17]所示,其表达式如下
(2)
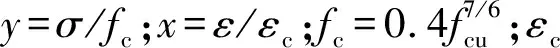
混凝土弹性阶段泊松比为0.2,塑性阶段采用塑性损伤模型,其中流动偏角取0.1,双轴等压时强度与单轴强度之比取1.225,拉、压子午线上第二应力不变量比值取0.667,黏性系数和剪胀角分别为0和40°。
钢材的应力-应变关系如图9所示,其表达式见式(3)

图9 钢材应力-应变曲线
(3)
式中:Es为钢材弹性模量;εe为钢材弹性段应力最大值fp下的应变,取εe=0.8fy/Es;εe1,εe2,εe3为塑性和应变硬化范围内的各种应变,其中εe1=1.5εe,εe2=10εe1,εe3=100εe1。
3.2 计算结果
4个圆端形钢管混凝土轴压短柱极限承载力试验值Nuo与有限元计算值Ne比较见表3。有限元计算值与试验值吻合良好并偏于安全。有限元计算结果破坏形态如图3所示,ABAQUS非线性有限元软件得到的典型荷载-应变全曲线与试验结果的比较如图4所示。由图4可知,对于钢管厚度为4 mm的试件,其曲线拟合结果较好,对于钢管厚度为6 mm的试件,其峰值后曲线差异较大,这是因为钢管厚度为6 mm的试件钢管对核心混凝土约束效应过大,混凝土强度过小,混凝土强度无法充分利用。图10为试件RCC1-4-60与试件RCC1-4-120峰值荷载处外部钢管与核心混凝土接触应力。由图10(a)可知,对于圆心角为60°的试件,峰值荷载处接触应力主要集中于角部,圆弧段接触应力值较低。对试件RCC1-4-120外钢管与核心混凝土的接触应力进行分析,结果表明:平直段与圆弧段交点处接触应力较强,圆弧段钢管与混凝土具有明显接触效应,但其接触应力较角部弱。比较可知,试件RCC1-4-60的角部接触应力较强,而试件RCC1-4-120圆弧段接触应力较强。核心混凝土所受整体约束效应为角部约束与圆弧段约束共同作用的结果,对于圆心角为60°的试件,角部约束起主要约束作用,而对于圆心角为120°的试件,圆弧段与角部同时对核心混凝土具有约束作用。

图10 峰值荷载处接触应力(单位:MPa)
3.3 参数分析
在验证有限元模型正确的基础上,分别对圆心角60°和圆心角120°的试件进行参数分析,分析其在不同钢材强度、混凝土强度、宽厚比、高宽比下的荷载-轴向应变关系及约束作用变化规律。本文共设计32个圆端形钢管混凝土试件,圆心角为60°的试件与圆心角为120°的试件各16个,表4为圆心角为60°的圆端形钢管混凝土主要参数,表5为圆心角为120°的圆端形钢管混凝土主要参数。

表4 圆端形钢管混凝土主要参数(θ=60°)
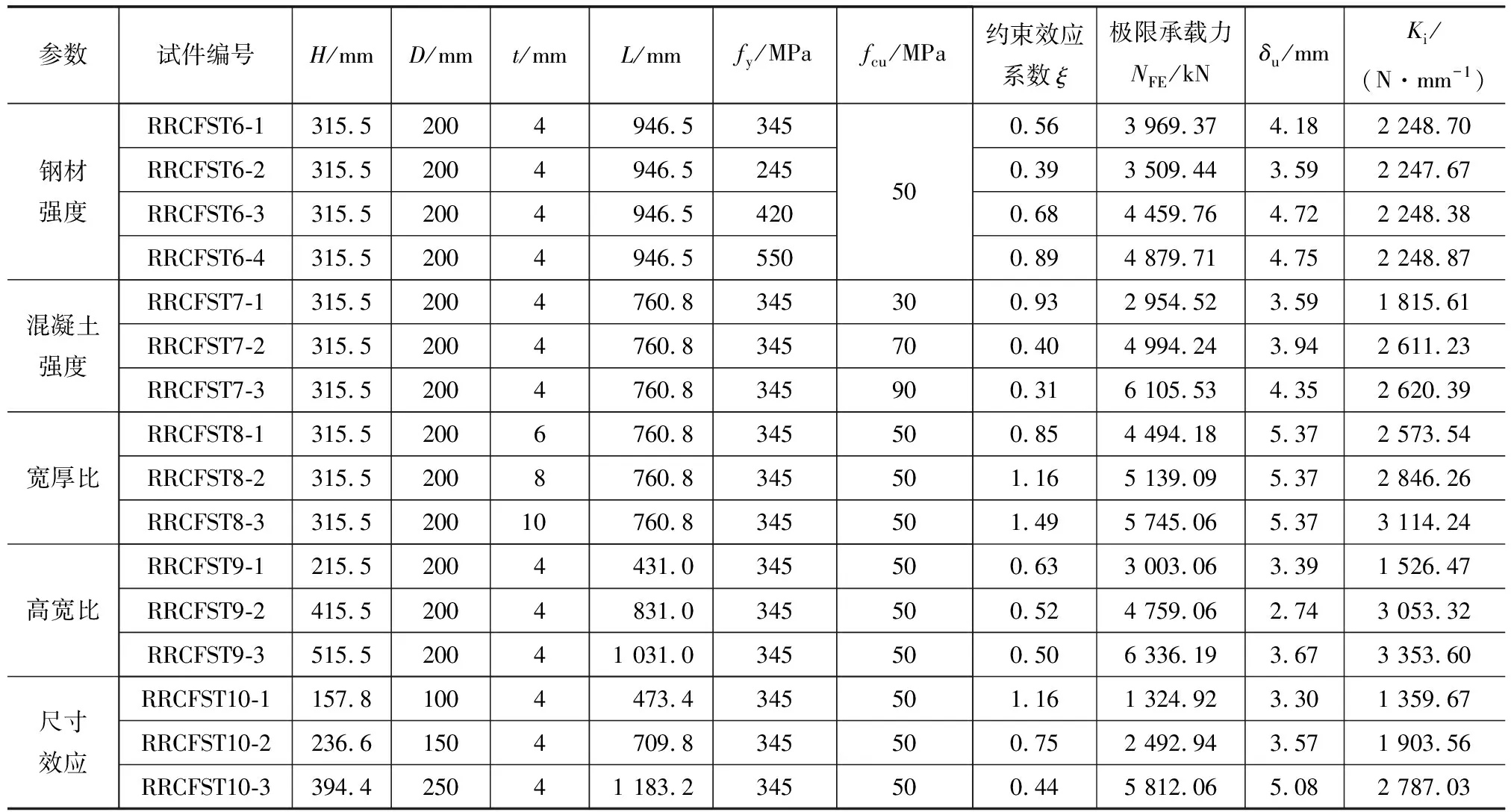
表5 圆端形钢管混凝土主要参数(θ=120°)
3.3.1 钢管强度
对4种不同强度(235,345,420,550 MPa)的钢管进行参数分析,其轴向荷载-轴向应变曲线如图11(a)和12(a)所示。结果表明,对于圆心角为60°和圆心角为120°的试件,随着钢管强度的增加,圆端形钢管混凝土试件的承载力逐渐增大,但其轴向初始刚度大致相同。对于圆心角为60°的试件,随着钢管强度由235 MPa增大到345,420,550 MPa,钢管混凝土极限承载力分别增加了16.5%,27.3%和45.3%。对于圆心角为120°的圆端形钢管混凝土试件,其轴压极限承载力与钢管强度为235 MPa的试件相比增加了13.1%,27.1%和39.0%。
3.3.2 混凝土强度
图11(b)和图12(b)给出了不同混凝土强度对轴向荷载-轴向应变曲线的影响。随着混凝土强度的增加,圆心角为60°和120°的圆端形钢管混凝土的轴向荷载值与初始刚度均逐渐增大,其峰值后曲线随着混凝土强度的增大下降段逐渐陡峭。圆心角为60°的圆端形钢管混凝土强度由30 MPa增加到50,70,90 MPa时,其极限承载力分别增加了35.2%,88.2%和128.7%,而对于圆心角为120°的试件,其轴压极限承载力分别增加了34.3%,69.0%和106.6%。
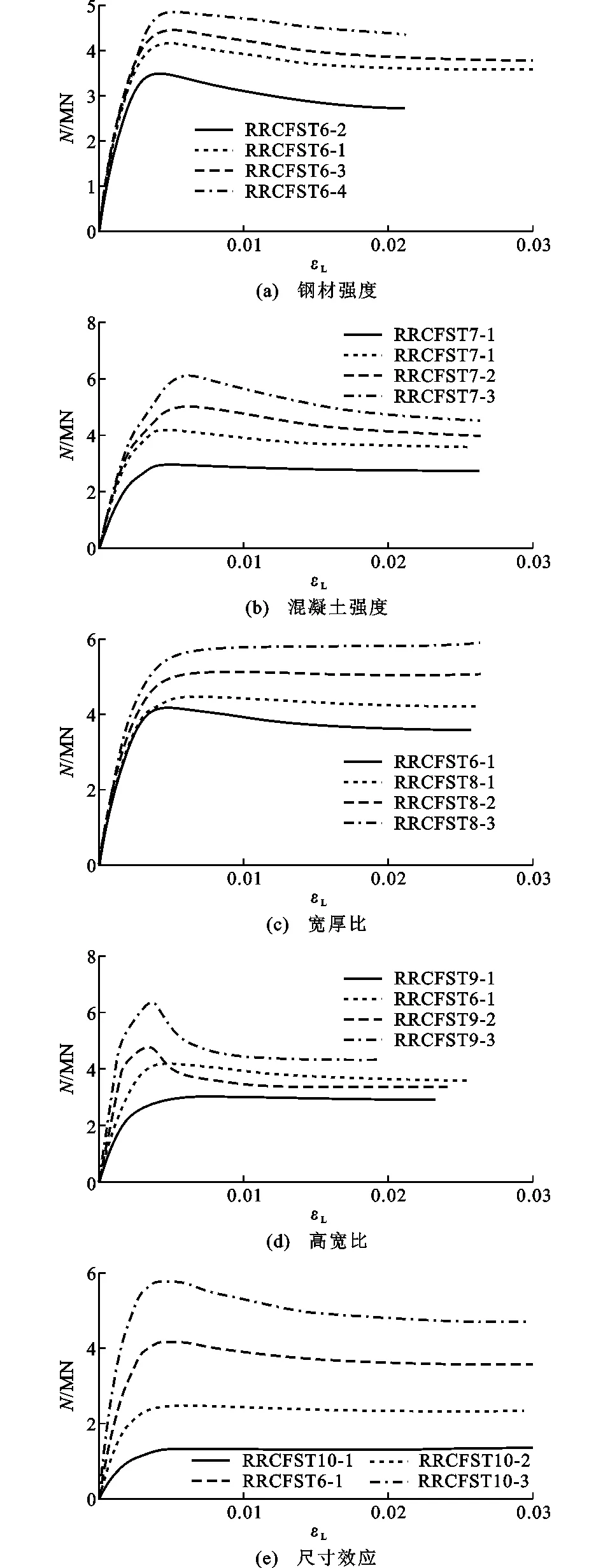
图12 各参数对N-εL曲线的影响(θ=120°)
3.3.3 宽厚比
图11(c)为宽厚比分别为50.0,33.3,25.0和20.0时,圆心角为60°的圆端形钢管混凝土短柱试件轴向荷载-应变关系曲线。随着宽厚比的增大,试件极限承载力和初始刚度逐渐降低。与宽厚比为50.0的试件相比,宽厚比为33.3,25.0,20.0的试件极限承载力分别增大了13.0%,23.4%和35.6%,而初始刚度增大了13.5%,22.0%,26.8%。

图11 各参数对N-εL曲线的影响(θ=60°)
对于圆心角为120°的圆端形钢管混凝土试件,与宽厚比为50.0的试件相比,宽厚比为33.3,25.0,20.0的试件极限承载力增大了10.5%,21.8%和30.9%,而初始刚度增大了9.0%,17.4%和27.8%。
3.3.4 高宽比
对圆心角为60°和120°的圆端形钢管混凝土高宽比不同的试件进行轴向荷载-轴向应变曲线分析。由图11(d)所示,随着高宽比的增大,试件的极限承载力逐渐增大,但在达到承载力峰值后试件延性逐渐降低。与高宽比为1.27的试件相比,高宽比为1.77,2.27和2.77的试件极限承载力分别增加了43.35%,76.41%和122.30%,而初始刚度增加了25.85%,64.43%和39.72%。对于圆心角为120°的试件,随着高宽比增大,试件的极限承载力与高宽比为1.08的试件相比,高宽比为1.58,2.08,2.58的试件极限承载力分别增加了32.2%,58.5%,111.0%,而试件初始刚度增加了47.3%,100.0%和119.7%。
3.3.5 尺寸效应
随着横截面的增加,圆端形钢管混凝土轴向极限荷载与初始刚度逐渐增大。与试件RRCFST1-1相比,试件RRCFST5-1,RRCFST5-2,RRCFST5-3的轴向极限荷载分别为其36%,63%和1.43倍,而初始刚度分别为试件RRCFST1-1的61%,77%和1.21倍。随着横截面面积的增大,圆端形钢管混凝土试件峰值荷载的增加呈线性分布,如图13所示,其中N0为试件RRCFST1-1的极限承载力值,A为圆端形钢管混凝土试件的横截面面积,A0为试件RRCFST1-1的横截面面积。对于圆心角为120°的试件,与试件RRCFST6-1相比,试件RRCFST10-1,RRCFST10-2,RRCFST10-3的极限承载力分别为试件RRCFST6-1的33%,63%和1.46倍,而初始刚度分别为RRCFST6-1的60%,87%和1.24倍。这表明,尺寸效应对圆心角为60°和120°的短柱极限承载力与初始刚度具有相同的影响。
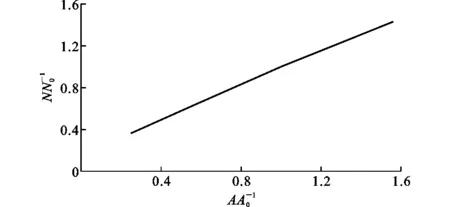
图13 横截面面积对轴向压缩强度的影响
4 承载力统一计算公式
圆心角为60°和圆心角为120°的圆端形钢管混凝土试件与圆心角为180°的钢管混凝土试件约束效应类似。文献[8]中提出了圆心角为180°的圆端形钢管混凝土短柱轴压极限承载力Nu,d计算公式
Nu,d=fcAc(1+KФ)
(4)
式中:Ф为套箍指标,Ф=fyAs/(fcAc);K为套箍系数。
随着高宽比的增大,外包钢管对核心混凝土的约束效应均逐渐减弱,当H/D=4时,2种材料基本单独工作。对32组参数数据进行分析,得到套箍系数K与高宽比的关系如图14所示。
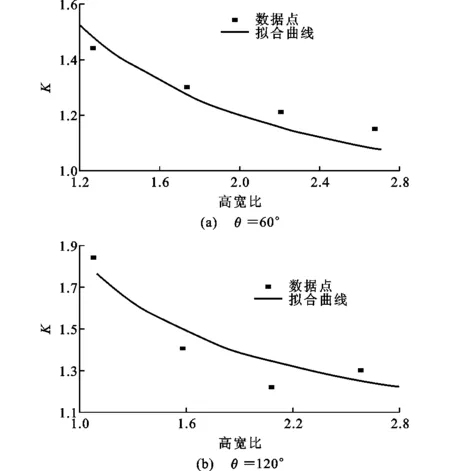
图14 K与高宽比的关系
通过拟合可得
(5)
综合圆心角为60°与120°的结果,可将其统一为
(6)
式中:A=0.39θ/π+0.61;E=0.12θ/π+0.9。
将式(6)代入式(4),可得圆端形钢管混凝土轴压短柱极限承载力Nu计算式为
Nu=fcAc[1+(A+ED/H)Ф]
(7)
轴压短柱算例极限承载力有限元计算结果Ne与采用式(7)得到的计算结果Nu对比如表6和图15所示,对于圆心角为60°的试件,2种方法计算得到的轴压短柱极限承载力比值的平均值为0.970,离散系数为0.003。对于圆心角为120°的试件,其极限承载力平均值与离散系数分别为0.972与0.004,可见采用式(7)所得的计算值与有限元计算值较为接近。
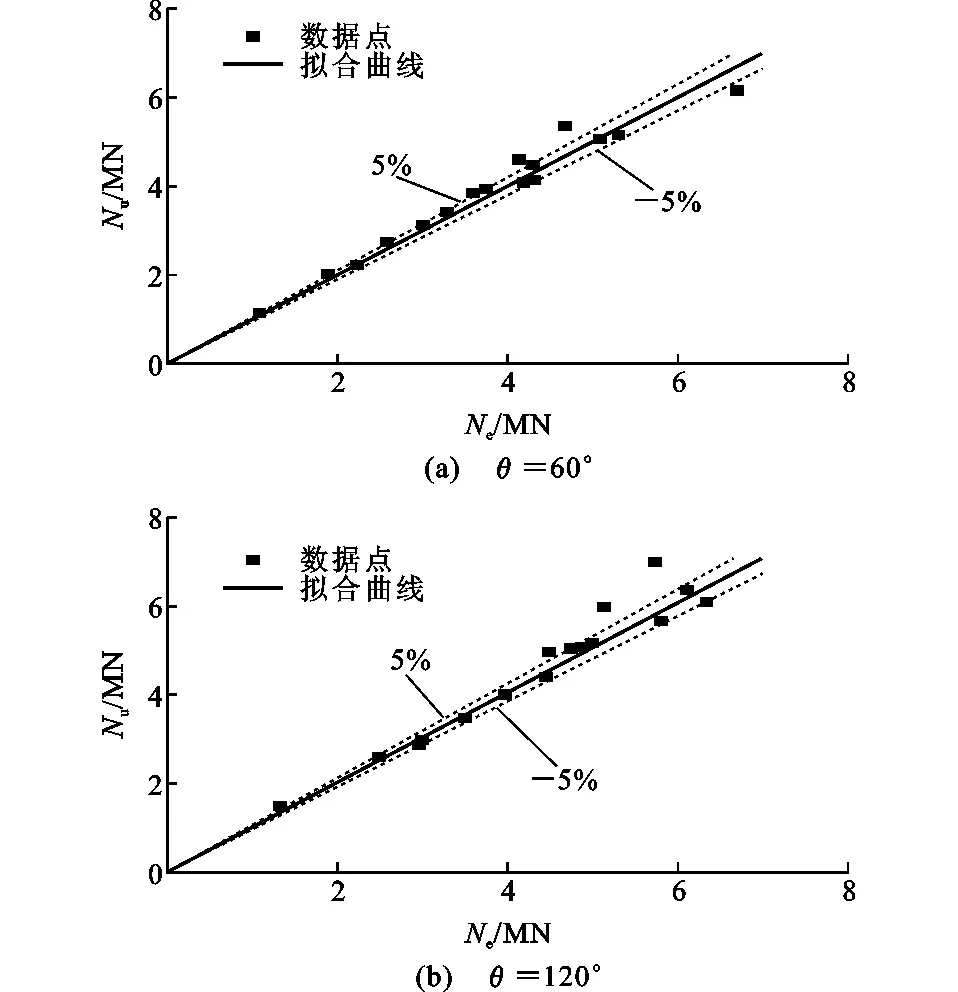
图15 公式(7)计算的Nu与Ne比较

表6 Nu与Ne比较
由表3可知:4个试件的试验结果与有限元计算结果比值的均值为1.04,方差为0.003;4个试件的试验结果与式(6)计算结果比值的均值为1.00,方差为0.004。由此可见,与试验结果相比,2种理论都偏于保守,且公式计算结果较有限元计算结果准确。
5 结 语
(1)对圆心角为60°和圆心角为120°的圆端形钢管混凝土轴压短柱进行轴压试验。结果表明,在其他条件相同的情况下,圆端形钢管混凝土轴压短柱的极限承载力随着钢管壁厚及圆心角的增大而增大。当圆心角从60°增大至120°时,强度指标降低,表明核心混凝土受到的整体约束效应降低。
(2)基于合理本构关系,采用ABAQUS有限元软件对圆端形钢管混凝土轴压短柱进行三维实体有限元模拟。结果表明:当圆心角由60°增大到120°时,圆弧段约束效应增强,角部约束效应减弱,整体约束效应减弱,计算结果与试验结果吻合良好。
(3)采用ABAQUS有限元软件进行参数分析,建立了圆心角分别为60°和120°的圆端形钢管混凝土轴压短柱极限承载力实用统一计算公式,公式计算结果与有限元计算结果吻合良好。目前对圆端形钢管混凝土圆心角的研究较少,研究成果可为圆端形钢管混凝土(包括圆形与矩形)承载力统一公式提供理论基础。
