UHPFRC与钢筋黏结-滑移模型

康少波，汪若云，王丹丹

(1.重庆大学 土木工程学院，重庆 400045; 2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045)

0 引 言

作为一种新型水泥基复合材料，超高性能纤维混凝土(Ultra-high Performance Fiber Reinforced Concrete,UHPFRC)具有良好的力学性能，与普通混凝土相比，抗拉、抗压强度提高(抗拉强度不低于150 MPa，抗压强度不低于6 MPa)，延性较好，且开裂后仍具有一定的抗拉强度[1]。UHPFRC主要用做承重构件或用做拼缝材料，例如桥墩、柱等。现有工程应用包括魁北克行人桥(1997年，第1个UHPFRC结构)和肖尼西轻轨站(2013年，预制UHPFRC防水屋顶和外墙)等。

近年来，随着UHPFRC应用范围逐渐扩大，钢筋与UHPFRC之间的黏结性能也日益受到重视。钢筋与UHPFRC之间的黏结性能是两者协同工作的基础，直接影响构件的承载力和变形能力以及超静定结构的应力重分布。黏结的强弱对裂缝宽度、受拉刚化和塑性铰的转动能力等均有显著影响[1-2]。

钢筋与普通混凝土之间的黏结强度主要受钢筋强度、混凝土强度、钢筋周围混凝土保护层厚度以及可能存在的外箍筋约束效应的影响[3]。UHPFRC中钢纤维的存在可抑制裂缝的发展，提高混凝土的延性，从而增强钢筋与UHPFRC之间的黏结性能。Marchand等[1,4-12]对UHPFRC与钢筋之间的黏结性能进行试验研究，讨论混凝土保护层厚度、钢筋埋置长度、纤维掺量等对黏结性能的影响。Sturm等[5]提出了钢筋黏结-滑移曲线，并将黏结-滑移模型分为2种类型,即有屈服平台与无屈服平台。当保护层厚度足够时，黏结-滑移模型服从有屈服平台分布，当保护层厚度较小时，钢筋易出现无屈服平台的黏结-滑移模型。Marchand等[1]开展了钢筋的拔出试验，确定了钢筋直径、埋置长度和混凝土覆盖层厚度对黏结性能的影响。基于试验结果，提出了局部黏结应力-滑移曲线，其计算结果与试验结果较为吻合，但是研究并未将局部黏结-滑移关系与埋置长度较长的钢筋整体黏结-滑移性能相关联，因此无法判断局部黏结-滑移模型在分析钢筋整体性能时的准确性。

采用不同局部黏结-滑移模型开展理论分析，研究不同埋置长度钢筋的整体黏结性能，并与试验结果进行对比，验证理论模型的准确性，确定钢筋埋置长度及荷载水平对黏结性能的影响规律。

1 局部黏结-滑移模型

早期钢筋在普通混凝土中的黏结-滑移关系大都为基于试验的数理统计模型[13-18]，徐有邻等[19]对试验数据进行统计回归和应力状态分析，建立了全过程黏结-滑移模型。针对在UHPFRC中埋置的钢筋，文献[1]中给出了2种钢筋局部黏结-滑移模型，分别为修正FIB模型和Marchand模型。

1.1 修正FIB模型

FIB规范建议的黏结应力-滑移(τ-S)关系(图1)为

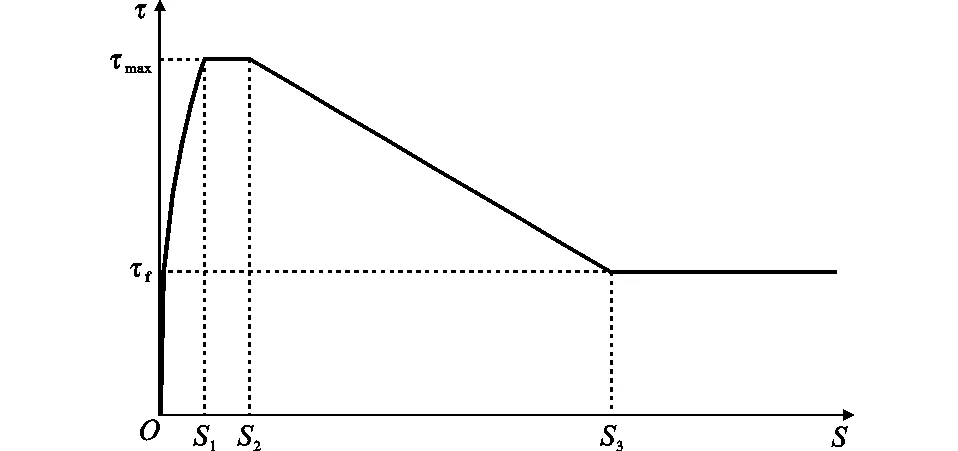
图1 修正FIB黏结-滑移曲线

(1)

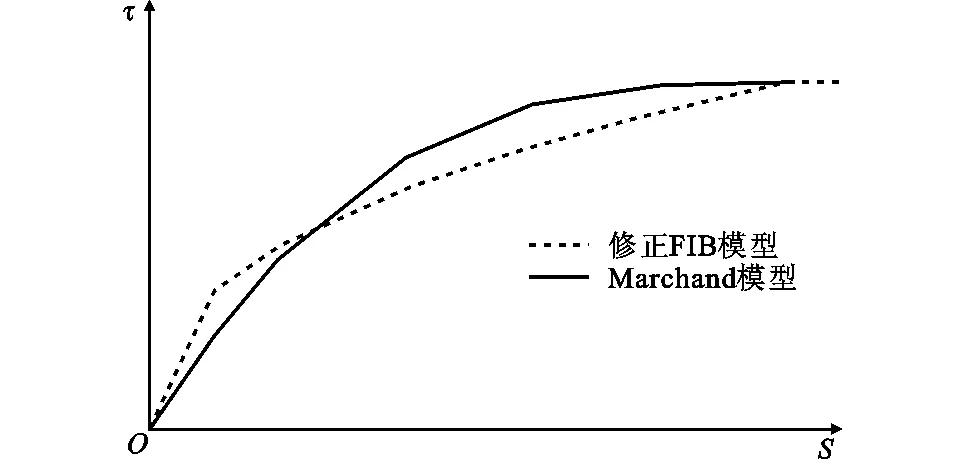
图2 黏结-滑移曲线上升段对比

1.2 Marchand模型

修正FIB模型的上升段与试验结果存在一定差异，不能准确反映钢筋与UHPFRC之间的黏结特征。因此，基于试验结果，Marchand将黏结-滑移曲线的上升段取为三次多项式，见公式(2)，其他阶段的表达式均与修正FIB模型相同。Marchand模型与修正FIB模型的对比见图2。

(2)

式中：β=3；S1=0.1 mm。

采用局部黏结-滑移模型计算埋置钢筋的黏结应力和应变时，通常假定混凝土的变形较小，钢筋与混凝土之间的相对滑移与钢筋的变形相同。

在黏结区域钢筋上取微小长度dx，建立变形协调方程

(3)

式中：S(x)为钢筋微段的滑移量；Sf为钢筋自由端的滑移量；ε(x)为钢筋微段的应变。

除变形协调条件外，钢筋微段需满足平衡条件

πddxτ(x)=As[σ(x+dx)-σ(x)]

(4)

(5)

式中：As为钢筋横截面面积；τ(x)为钢筋表面与混凝土之间的黏结应力，可由钢筋微段滑移量根据黏结-滑移模型确定；d为钢筋直径；σ(x)和σ(x+dx)分别为微段两端的钢筋应力，其中σ(x)可根据钢筋的应力-应变关系获得。

2 试验参数

为对比分析不同模型的准确性，选取文献[1]中的钢筋拔出试验结果进行验证，试验装置如图3所示。选取4个埋置长度不同的试件开展分析，试件参数如表1所示。UHPFRC强度为205 MPa；钢筋直径为12 mm，埋置长度分别为2.5d，4d，8d。试件72-8-5与试件194-8-5的钢筋直径、埋置长度均相同，但其保护层厚度不同，试件194-8-5的保护层厚度为194 mm，而试件72-8-2的保护层厚度为30 mm。试件的破坏模式为钢筋断裂破坏(F)和拔出破坏(PF)，4个试件破坏时UHPFRC均未发生劈裂破坏。

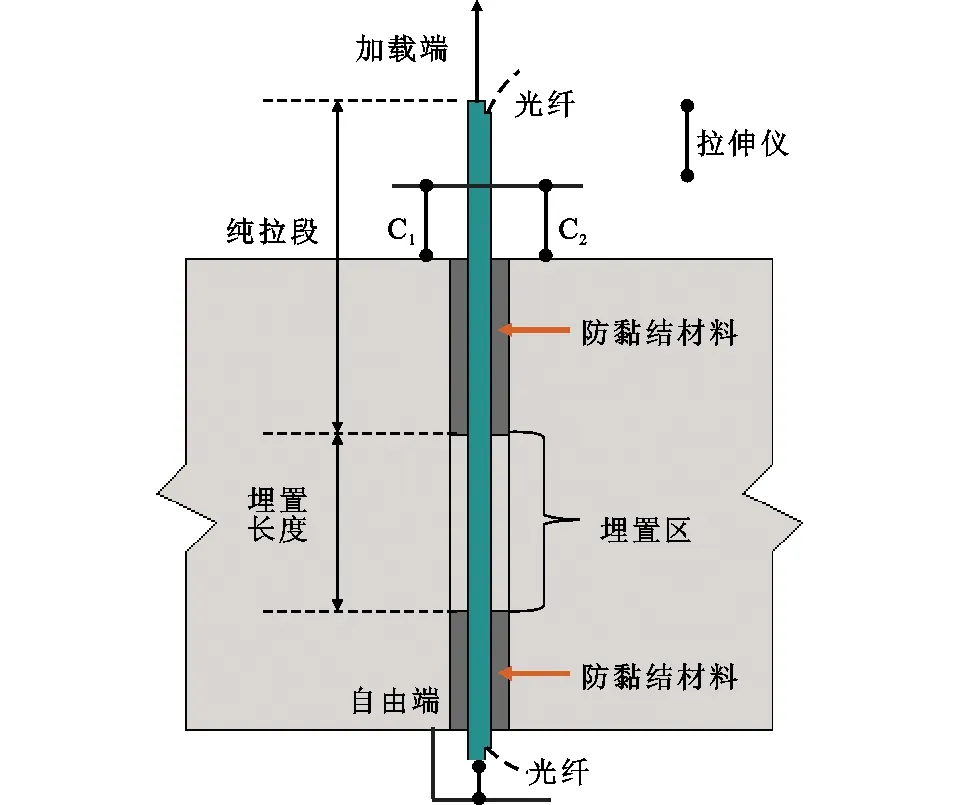
图3 试验装置

表1 试件参数

钢筋分为开槽与未开槽钢筋，开槽钢筋的屈服强度fy与极限强度fu分别为516.0 MPa和577.4 MPa。未开槽钢筋的屈服强度和极限强度分别为532.0 MPa与590.5 MPa，其弹性模量与强化模量见表2。

表2 钢筋性能

由于微小钢筋滑移会引起较大的黏结应力，为获得钢筋整体黏结应力的分布情况，钢筋应变的测量至关重要。Tassios等[20]利用光学方法测量了钢筋与混凝土截面之间的应变和滑移，测量结果较为精确，但装置复杂，不易开展。Marchand等[1]将钢筋表面开槽，采用光纤应变系统测量沿钢筋埋置长度的应变分布，见图3。

3 模型验证

钢筋微段长度取值对分析精度和计算效率有显著影响。分析时，对埋置长度为30 mm的钢筋，dx取2 mm和3 mm为宜。对埋置长度为48 mm的钢筋，dx取3 mm和4 mm为宜。对埋置长度为96 mm的钢筋，dx宜取6 mm。

为验证理论分析模型的准确性，取钢筋加载端的应变计算值与试验值相等或接近，对比沿钢筋埋置长度的应变及黏结应力分布。

3.1 钢筋埋置长度为2.5d

将修正FIB模型和Marchand模型计算所得的钢筋应变与试验结果进行对比，如图4所示。其中埋置长度为2.5倍钢筋直径，即30 mm，微段计算长度dx为2 mm。由图4可知，当加载端荷载分别为12，36，48 kN时，修正FIB模型和Marchand模型曲线与试验曲线吻合较好。

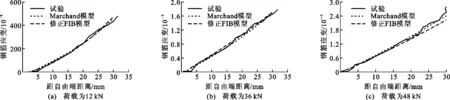
图4 试件194-2.5-5钢筋应变对比

图5为试件194-2.5-5沿埋置钢筋长度的黏结应力分布。对比修正FIB模型与Marchand模型计算结果发现，当荷载为12 kN时，钢筋自由端处修正FIB模型计算的黏结应力小于Marchand模型计算的黏结应力，而加载端处Marchand模型计算的黏结应力大于修正FIB模型计算的黏结应力。当荷载逐渐增大至36 kN时，自由端处修正FIB模型计算的黏结应力大于Marchand模型黏结应力，而加载端修正FIB模型计算的黏结应力小于Marchand模型计算的黏结应力，黏结应力沿埋置钢筋逐渐一致。当荷载为48 kN时，Marchand模型计算的黏结应力与修正FIB模型计算的黏结应力较为吻合，沿钢筋埋置长度的黏结应力分布较为均匀，表明当钢筋埋置长度较短且荷载较大时，其黏结应力接近于钢筋的平均黏结强度。

图5 试件194-2.5-5黏结应力对比

3.2 钢筋埋置长度为4d

图6为试件54-4-2的钢筋应变分布曲线，其中钢筋埋置长度为4倍钢筋直径，即48 mm。当加载端荷载为12 kN时，Marchand模型计算的钢筋应变与试验结果吻合良好，而修正FIB模型计算的钢筋应变在靠近钢筋自由端处显著低于试验结果。随着加载端荷载逐渐增大，Marchand模型与修正FIB模型计算结果逐渐靠近。

图6 试件54-4-2钢筋应变对比

图7为试件54-4-2沿钢筋埋置长度内的黏结应力分布。对比发现，2种模型的计算结果明显不同，当荷载为12 kN时，Marchand模型计算的加载端黏结应力低于修正FIB模型的计算结果，而在自由端的黏结应力高于修正FIB模型的计算结果。当荷载增大至36 kN时，Marchand模型加载端和自由端黏结应力均高于修正FIB模型计算结果。随着荷载逐渐增大至54 kN，Marchand模型在加载端的黏结应力高于修正FIB模型的计算结果，而在自由端的黏结应力低于修正FIB模型的计算结果。不同荷载下黏结应力分布规律的不同主要是由不同黏结-滑移模型上升段引起。

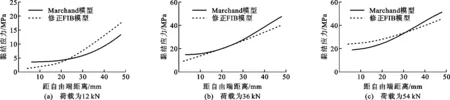
图7 试件54-4-2黏结应力对比

3.3 钢筋埋置长度为8d

图8为试件72-8-5沿钢筋埋置长度的钢筋应变分布，其埋置长度为8倍钢筋直径，即96 mm。由图8可知：当荷载为13 kN时，Marchand模型计算所得的钢筋应变分布与试验结果较为吻合，而修正FIB模型的计算结果与试验结果相差较大；随着荷载的逐渐增大，Marchand模型与修正FIB模型的试验曲线逐渐靠近，并与试验曲线吻合良好。

图8 试件72-8-5钢筋应变对比

图9为试件72-8-5沿钢筋埋置长度内的黏结应力分布。由图9可知，当荷载为13 kN时，修正FIB模型在自由端的黏结应力为0，而Marchand模型计算结果高于修正FIB模型，随着荷载值逐渐增大，修正FIB模型计算的黏结应力段逐渐增大，其黏结应力计算结果与Marchand模型计算结果逐渐靠近。

图9 试件72-8-5黏结应力对比

图10为试件194-8-5的钢筋应变分布曲线，钢筋埋置长度为96 mm，即8倍钢筋直径。由图10可知，当钢筋加载端荷载相同时，Marchand模型和修正FIB模型均低估了沿钢筋埋置长度的拉应变。当荷载较小时，采用Marchand模型的计算结果较为精确，修正FIB模型计算的加载端附近的钢筋应变与试验值较为吻合，但自由端的钢筋应变显著小于试验值；当荷载逐渐超过极限荷载的60%时，修正FIB模型与Marchand模型计算结果与试验结果吻合良好。

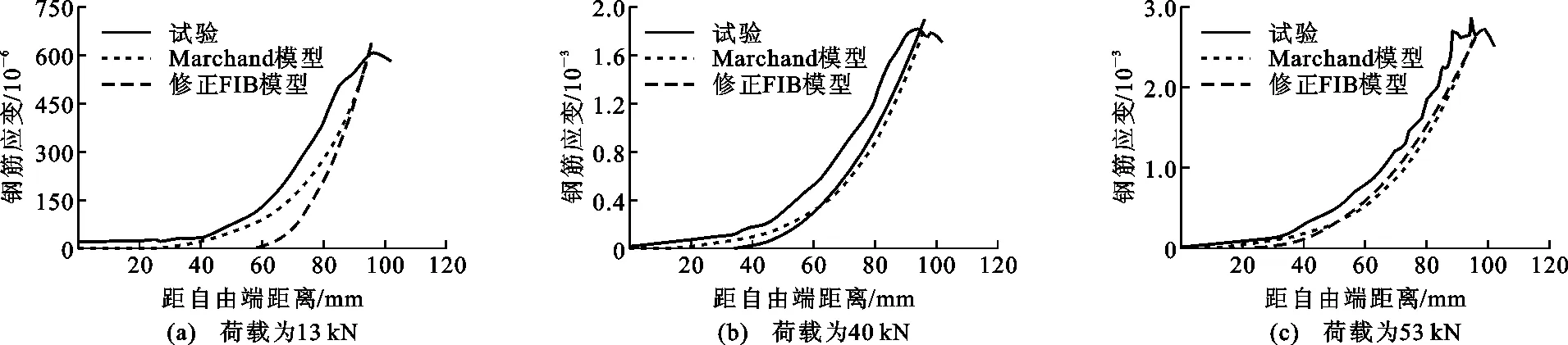
图10 试件194-8-5钢筋应变对比

与埋置长度为2.5d(30 mm)和4d(48 mm)的试验钢筋应变相比，埋置长度为8d(96 mm)的钢筋应变在自由端附近为0，随距自由端距离逐渐增大，钢筋应变缓慢增大，呈现出明显的非线性分布，而埋置长度为2.5d时，钢筋应变迅速增大，分布近似线性。

与图4对比发现：当钢筋埋置长度较短时，Marchand模型计算的钢筋应变分布较为准确；当钢筋的埋置长度较长时，与试验结果相比，Marchand模型低估了加载端附近的钢筋应变值。这可能是因选取的钢筋微段长度较大引起的。适当减小钢筋微段长度可提高计算精度，但需要更长的运行时间。

图11为试件194-8-5在不同荷载作用下钢筋与UHPFRC之间的黏结应力分布。由图11可知，Marchand模型计算的钢筋黏结应力沿钢筋埋置长度呈明显的非线性分布，钢筋自由端黏结应力较小，而加载端黏结应力较大。采用修正FIB模型计算钢筋与UHPFRC之间的黏结应力时，仅能得到有限长度范围内的黏结应力，而钢筋自由端的黏结应力为0，这表明通过修正FIB模型获得的承担施加荷载所需的埋置长度小于实际埋置长度。比较图11(a)，(c)发现，随着荷载的增大，修正FIB模型的计算精确逐渐提高。

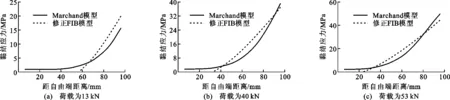
图11 试件194-8-5黏结应力对比

与埋置长度为2.5d(30 mm)，4d(48 mm)的沿钢筋埋置长度的黏结应力相比，钢筋埋置长度为8d(96 mm)的黏结应力分布呈现明显的非线性，而埋置长度为2.5d时，随着荷载值增大，黏结应力分布逐渐均匀，分布近似为直线段。

4 结 语

(1)当钢筋埋置长度较小(2.5d)时，Marchand模型计算结果与修正FIB模型计算结果均与试验结果吻合良好。荷载较大时，黏结应力沿钢筋埋置长度均匀分布。

(2)当钢筋埋置长度逐渐增大(2.5d～8d)，荷载较小时，Marchand模型钢筋应变计算结果与试验结果吻合良好，而修正FIB模型计算的钢筋应变与试验结果误差较大。随着荷载逐渐增大，误差逐渐减小，Marchand模型结果与修正FIB模型结果均与试验结果较为吻合。钢筋埋置长度较大时，自由端与加载端应力值显著不同。