复合型加载条件下HCCD试样应力强度因子的研究

杨 旺， 巫绪涛， 仰 涛

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引 言

由于具有强度高、造价低、材料来源广泛、耐久性好等优点,混凝土在现代土木工程中被大量使用。但混凝土内部不可避免地存在大量原生微裂纹,往往导致结构没有达到承载力时就发生破坏,这是由裂纹的快速扩展而发生的低应力脆性断裂。应力强度因子反映了裂纹尖端弹性应力场的强弱,对于建立脆性断裂准则及研究构件内的裂纹扩展具有重要的意义。为了建立脆性断裂准则,人们利用巴西圆盘试验时试样内部可以产生拉应力和切应力的特点,通过在圆盘试样内预制裂纹,并改变裂纹与载荷夹角,从而实现纯Ⅰ型、纯Ⅱ型及复合型断裂。但由于预制裂纹较困难、裂尖应力强度因子较小以及加载处存在较严重的应力集中,人们对带裂纹的巴西圆盘试验进行了多种改进。文献[1-5]分别研究了带裂纹扁平巴西圆盘、人字型切槽巴西圆盘、中心直裂纹平台巴西圆盘、带裂纹中心圆孔圆盘(hollow centre cracked disc,HCCD)的改进形式。其中HCCD试验很好地解决了上述难题,得到了一些学者的关注,但由于具有较复杂的边界条件,HCCD试样裂尖的应力强度因子尚无法得到理论解。文献[6-8]均采用有限元方法给出了拟合公式,但为了减少变量,上述公式均固定了试样的尺寸和加载角,不具有普适性,且重点研究纯Ⅰ型断裂,复合型断裂研究不充分。

本文对复合型加载条件下HCCD试验进行了数值模拟,结合量纲分析得到了一般性的Ⅰ型和Ⅱ型应力强度因子拟合公式。该组公式同时包含裂纹倾角θ、圆盘内径r、裂纹长度a3个变量,当3个变量在较宽范围内变动时,公式均具有较高精度。且通过该组公式可以方便地计算各种条件下KⅠ/KⅡ及纯Ⅱ型断裂条件，从而方便了HCCD试验设计。

1 有限元模型及公式拟合

1.1 有限元模型

HCCD试验简图如图1a所示,其中,a为裂纹长度；R为试样外半径；r为试样内半径；θ为裂纹倾角；F为集中荷载。采用有限元软件ANSYS进行数值模拟,单元类型为SOLID186。由于裂纹尖端的应力奇异性,用不含奇异性的常规有限元计算,需要很密的网格,计算时间长且精度不高。因此通过KSCON命令在围绕裂尖一圈实现退化奇异等参元,且采用单元均匀变化的辐射式网格划分方式,如图1b所示。裂尖的应力强度因子用相互作用积分法计算。这种方法计算方便,适用性强,且对裂纹区域网格密度的依赖性小。试样采用线弹性本构,其弹性模量E为30 GPa；泊松比ν为0.2。试样厚度B为0.025 m,外圆半径R为0.05 m,内外圆半径比r/R从0.05变化至0.50,相对裂纹长度a/(R-r)从0.1变化至0.6,裂纹倾角θ从0°变化至30°,承受集中力F=1 000 N。

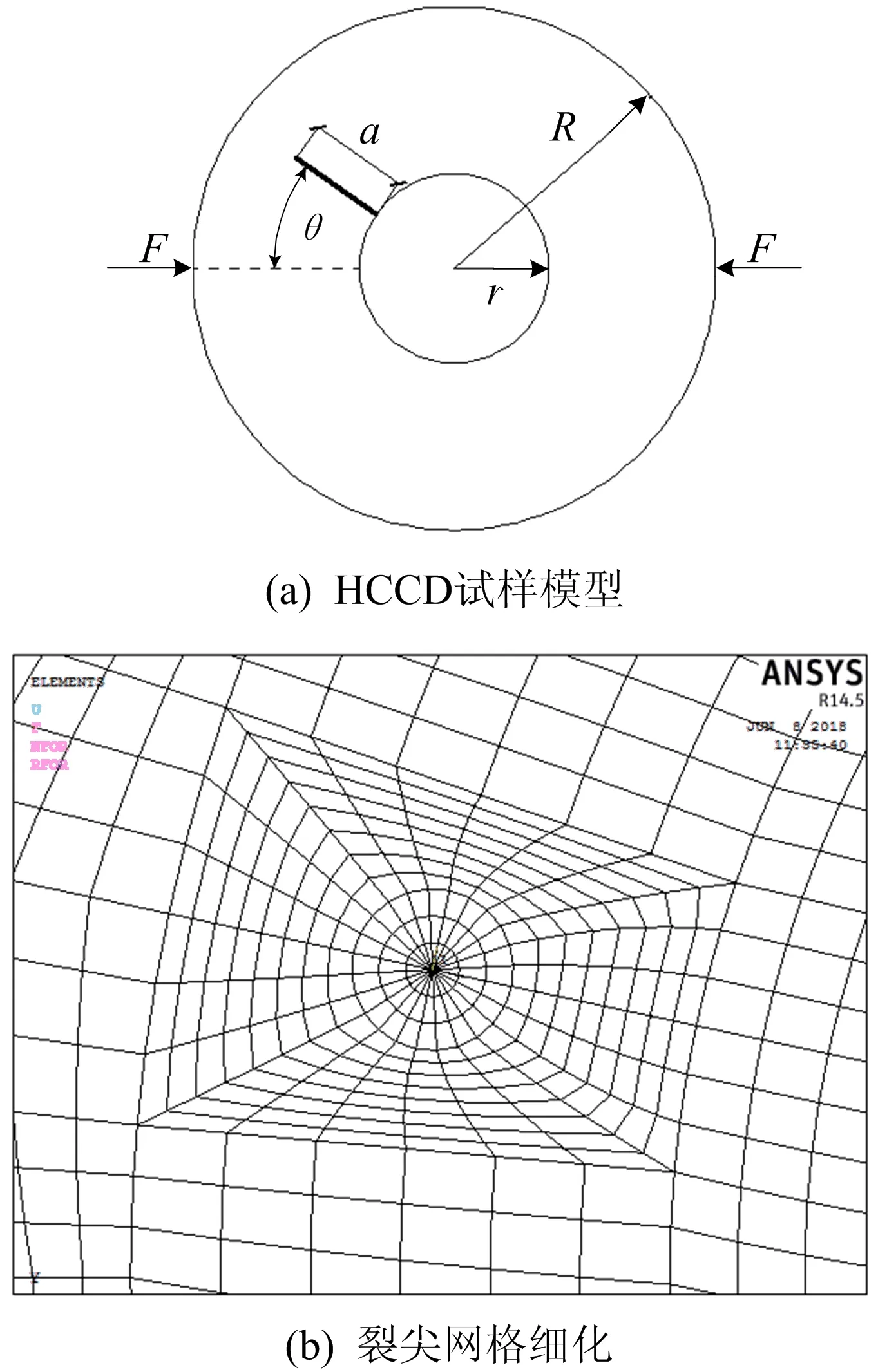
图1 复合型加载HCCD试验简图

1.2 Ⅰ型应力强度因子公式拟合

根据大量算例结果并结合量纲分析法,选择Ⅰ型应力强度因子KⅠ拟合公式的形式为:

(1)

(1)式的前半部分满足应力强度因子的量纲形式,f为无量纲形状因子,是相对裂纹长度a/(R-r)、内外半径比r/R、裂纹倾角θ的函数。为了分析方便,将(1)式转换为:

(2)

由数值模拟得到KⅠ的散点值,由(2)式计算f值。研究发现f随着cosθ的减小而单调递减,并且具有良好的线性关系,因此,对f采用以下形式,即

(3)

(3)式中的G和H都是关于r/R和a/(R-r)的函数,其变化规律具有相似性,因此采用相同的拟合形式,即

(4)

(5)

对于(4)式中的b0、b1、b2,分别采用以下公式进行拟合,即

(6)

(7)

(8)

其中,n0=0.56；n1=74.97；n2=0.06；n3=-1.06；n4=-0.29；m0=0.06；m1=-1.27；m2=1.54；d0=2.56；d1=18.60；d2=-39.25；d3=21.66。

对于(5)式中的c0、c1和c2,采用与(6)～(8)式相同的拟合形式,仅系数值不同,即

n0′=-1.14,n1′=-85.59,n2′=0.06,

n3′=1.40,n4′=-0.33;

m0′=-0.05,m1′=1.09,m2′=-1.29;

d0′=2.56,d1′=18.60,

d2′=-39.25,d3′=21.66。

采用上述公式计算复合型加载条件下HCCD试样的Ⅰ型应力强度因子,最大计算误差不超过9%。在a/(R-r)为0.2,r/R从0.05变化至0.50时其拟合效果如图2所示。

图2 KⅠ拟合效果

1.3 Ⅱ型应力强度因子公式拟合

根据量纲分析法,选择Ⅱ型应力强度因子KⅡ拟合公式的形式为:

(9)

(9)式的前半部分满足应力强度因子的量纲形式,Y为无量纲形状因子,与相对裂纹长度a/(R-r)、内外半径比r/R、裂纹倾角θ相关。为了方便分析,将(9)式转换为:

(10)

根据模拟的KⅡ值按(10)式计算Y,发现Y与a/(R-r)具有很好的线性关系,即

(11)

(11)式中的U和I都是关于r/R和θ的函数。分别采用的拟合形式如下：

(12)

(13)

(12)式中的q0拟合公式如下：

q0(θ)=e0+e1exp(e2θ)

(14)

其中的系数值分别为:e0=-0.38；e1=0.39；e2=0.02。

(12)式中的q1与q0具有相同形式,仅拟合系数值不同,即e0′=-0.03,e1′=-0.15,e2′=0.05。

(13)式中t0的拟合形式如下:

t0=k0+k1θ+k2θ2+k3θ3+k4θ4

(15)

其中的系数值分别为:k0=0.48；k1=-0.16；k2=0.02；k3=-0.96E-5；k4=1.28E-5。

(13)式中的t1与t0形式相同,只是系数值不同:k0′=-2.71；k1′=1.56；k2′=-0.12；k3′=4.00E-3；k4′=-5.14E-5。

采用上述公式计算复合加载条件下HCCD试样的Ⅱ型应力强度因子,其最大计算误差小于10%。在相对裂纹长度a/(R-r)为0.2时其拟合效果如图3所示。

图3 KⅡ拟合效果图

2 发生纯Ⅱ型断裂的起始位置

在r/R为0.3,不同裂纹倾角下,Ⅰ型应力强度因子KⅠ的值随相对裂纹长度a/(R-r)的变化如图4所示。

图4 KⅠ随a/(R-r)的变化关系

由图4可以看出,当r/R不变时,KⅠ的值随裂纹倾角的增大而减小,随a/(R-r)的增大单调递减。并且当裂纹倾角越大其下降趋势越快,最终趋向于0。这表示裂纹的扩展方式由Ⅰ-Ⅱ复合型逐渐转变至纯Ⅱ型。

根据数值模拟的结果,可以得到不同相对裂纹长度a/(R-r)、内外半径比r/R和裂纹倾角θ的情况下KⅠ值近似为0的点,即为开始发生纯Ⅱ型断裂的起始位置。当裂纹倾角θ大于20°时,也可以使用Ⅰ型应力强度因子公式计算得到纯Ⅱ型断裂的起始位置。使用公式计算和数值模拟的对比结果如图5所示。

图5 纯Ⅱ型断裂起始位置对比

3 结 论

(1) 本文对复合型加载条件下HCCD试验进行了数值模拟,得到Ⅰ型和Ⅱ型应力强度因子的拟合公式。

当裂纹倾角θ在0°～15°,内外圆半径比r/R在0.05～0.50,相对裂纹长度a/(R-r)在0.1～0.6的范围内时,KⅠ公式最大误差小于8%;当裂纹倾角θ在15°～30°,内外圆半径比r/R在0.05～0.50,相对裂纹长度a/(R-r)在0.1～0.4范围内时,KⅠ公式的最大误差小于9%;且当裂纹倾角θ等于0°时,该公式可以退化为文献[9]给出的纯Ⅰ型公式。

当裂纹倾角θ在0°～30°,内外圆半径比r/R在0.1～0.5,相对裂纹长度a/(R-r)在0.1～0.6的范围内时,KⅡ公式的最大误差小于10%。

(2) 当裂纹倾角θ大于20°时,可以使用本文得到的KⅠ公式计算纯Ⅱ型断裂位置。

上述结论大大方便了复合型HCCD试验设计,可以快速计算各种情况下的KⅠ/KⅡ及纯Ⅱ型断裂条件。