基于干扰对齐的井下多跳无线传感网络优化

卫 星, 李 亮, 陆 阳

(合肥工业大学 计算机与信息学院,安徽 合肥 230601)

0 引 言

井下无线传感网络是指布设于矿井巷道及岩壁,以多跳方式实时传输表征矿层、土壤、岩石、环境等各类参数的特殊传感器网络。由于受到路径损耗、反射或折射、多径衰落、机器噪声等因素的影响,井下无线信道复杂多变,无线信号传输损耗巨大。更为严重的是传感器节点之间的传输也存在着通信干扰,即处于发送状态的节点会对其通信范围内非目标接收节点造成干扰。因此,针对于井下无线传感网络干扰管理的研究成为近年来的研究热点之一。

目前井下无线传感网络干扰管理的研究多是针对单天线节点的路由及通信协议。文献[1]在保证最大化信噪比的前提下,通过研究瓶颈节点对网络吞吐量的影响,提出了一种基于贪心策略的跨层设计算法;文献[2]针对井下数据通讯协议提出了一种对传输应用层实现可靠数据传输的设计方法;文献[3]设计了一种可自我修正、自我调节的管理干扰的移动网络通信协议及调度策略。这些方法在本质上是利用干扰消除和时分多址技术实现了多对一的可靠传输,但效果受到井下固有信道特性的制约。

多输入多输出(multiple-input multiple-output,MIMO)技术能够有效利用井下的多径效应,成倍提高信道容量和质量,降低误码率,且不需要额外增加信道带宽,在井下无线传感网络中的应用前景广阔[4-5]。为了消除MIMO网络中每个接收节点的通信干扰,必须在单个天线进行目标数据流接收的同时,利用多个冗余天线接收干扰数据流,这种方式存在着较大的资源浪费(大部分天线没有用于数据传输)。

干扰对齐(interference alignment,IA)技术[6-9]是新兴的基于空间复用的干扰消除方法,其核心思想是利用信道传输特征在接收节点将多个非预期数据流(干扰流)在空间上“对齐”到某一特定方向,从而有效降低网络节点资源的消耗。文献[10-11]中仿真结果表明,在装备U个天线的V对节点自由通信网络的干扰信道中,整个网络的总自由度(即可用天线数目)逼近UV/2;文献[12]基于统计模型,提出一种自适应的方法来实现IA,与传统的固定模式IA相比有明显的优势;文献[13]研究了D2D通信系统和无中继通信系统中的IA,并给出整个模型的自由度上限。然而上述研究都是针对蜂窝基站的单跳网络模型,这些网络模型不适用于井下多跳MIMO网络。

本文以最大化井下多跳MIMO传感网络吞吐量(最小通信速率)为目标,在引入IA机制下,优化各时隙的节点状态及其收发数据流数分布;介绍了IA的基本思想;利用井下无线传感网络半双工、分时隙的特点,构建IA模型;建立了混合整数线性规划(mixed-integer linear programming,MILP)的系统优化模型。

1 干扰对齐原理

1.1 工作方式设定

井下MIMO无线传感网络工作方式设定如下:

(1) 每个节点均配备由多个天线组成的阵列,支持多数据流的同时传输。每个节点均为半双工工作方式,即任一时刻只能处于发送或接收状态的一种。通过调整发送节点和接收节点天线角度在空间中形成方向匹配,即可进行一组数据流的传输,因此将每个节点的天线个数定义为自由度,用于表征其可用资源。

(2) 网络支持多跳路由协议,且采用时间片轮转方式进行传输,即将系统工作时间划分为若干相等间隔的时隙,每个时隙内的节点状态和路由均已知,将路由协议指定的源节点、预期节点、数据流总数构成的三元组称为会话。

(3) 对于一个具体会话,源节点、预期节点之间传输的数据流,称为通信流;若源节点发送的数据流被其他节点(非预期节点)收到,则称之为干扰流。干扰消除方法如图1所示。在某一时隙发送节点A的任务同时经过无线信道发送2个通信流到接收节点B;在节点B处,使用天线1和天线4分别接收。若此时发送节点C、D分别执行发送任务到其他节点,则会对节点B形成2个不同空间方向的干扰流。为了实现干扰消除,节点B需要使用天线2、天线3，并调整空间的角度以分别接收这2个干扰流。

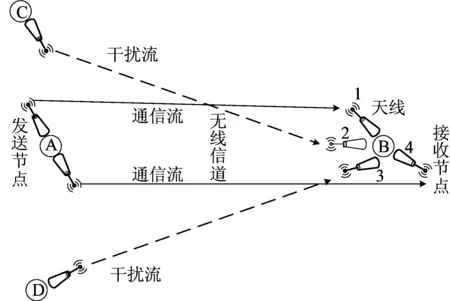
图1 干扰消除原理示意图

1.2 干扰对齐原理

IA是指对发送节点的数据流进行构造,使得在预期接收节点上,通信流顺利到达,同时在非预期的接收节点上,多个干扰流对齐到指定方向上。在发送节点上对数据流构造相当于在发送节点上对每个数据流的预编码向量进行设计,使得该数据流经过信道矩阵时被映射到指定方向上。由于多数干扰流被对齐到接收节点的同一方向上,可以使用较少资源来消除这些干扰。因此,IA减少了干扰消除所消耗的网络资源,使更多的网络资源可用于数据传输。

假设每个节点都配有3个天线,序对(T1,R1)、(T2,R2)、(T3,R3)、(T4,R4)上的数据流个数分别为2、2、1、1(序对表示2个节点间通信,前一个为发射节点,后一个为接收节点)。令Hji为Rj(j=1,2,3,4)和Ti(i=1,2,3,4)之间的信道矩阵,并且Hji均为满秩的3×3矩阵。

不采用IA时,R4需要消耗5个自由度来消除来自T1、T2、T3的干扰[11-12]。实际R4只有3个自由度,不可能消除所有的5个干扰流,也不能从T4收到任何通信流。IA实施机制如图2所示。图2中,实线表示通信流,虚线表示干扰流。采用IA可以把5个干扰流在空间上对齐为2个维度,R4只需要消耗2个自由度便可消除干扰,从而R4剩余1个自由度,用于从T4接收1个通信流。

图2 IA实施机制

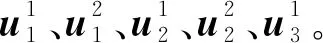
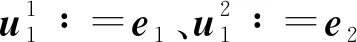
需要指出的是,实际的井下网络节点在不同时隙的情况较为复杂,井下实际异构网络存在多种通信方式,多节点间相互通信干扰严重。

2 干扰对齐策略

2.1 基本设定

多跳MIMO网络如图3所示。

图3 井下多跳MIMO网络

令N为网络节点的集合,N0为网络节点数;每个节点都安装了NA个天线;令F为会话集合,F0为会话数,s(f)和d(f)分别表示会话f的源节点和目的节点,其中f∈F。为了将数据流l从s(f)传输到d(f),允许网络内部的流分裂,可以将一次数据传输过程划分为K个时间间隙。其中，l∈L,L为网络里数据链接的集合,L0为数据链接数。

在第t(1≤t≤K)个时间间隙,令NT为发送节点数,NR为接收节点数,显然NT+NR=N0。令φ=(z1,z2,…,zL)表示网络中的传输自由度向量,zl为数据流数目,l为任意数据流。

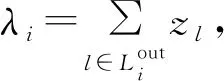
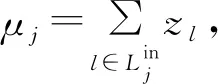
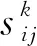
令Sij为从Ti到Rj的通信流集合,且有σij=|Sij|,Aij为从Ti到Rj干扰流集合,αij=|Aij|,因此存在σij+αij=λi。对于Aij中所有干扰流,Bij表示在Rj上可以被对齐的干扰流子集,且有βij=|Bij|。因此,从Ti到Rj的有效干扰流数目从αij降低到αij-βij。

2.2 干扰对齐约束

发送节点的IA约束如图4所示。

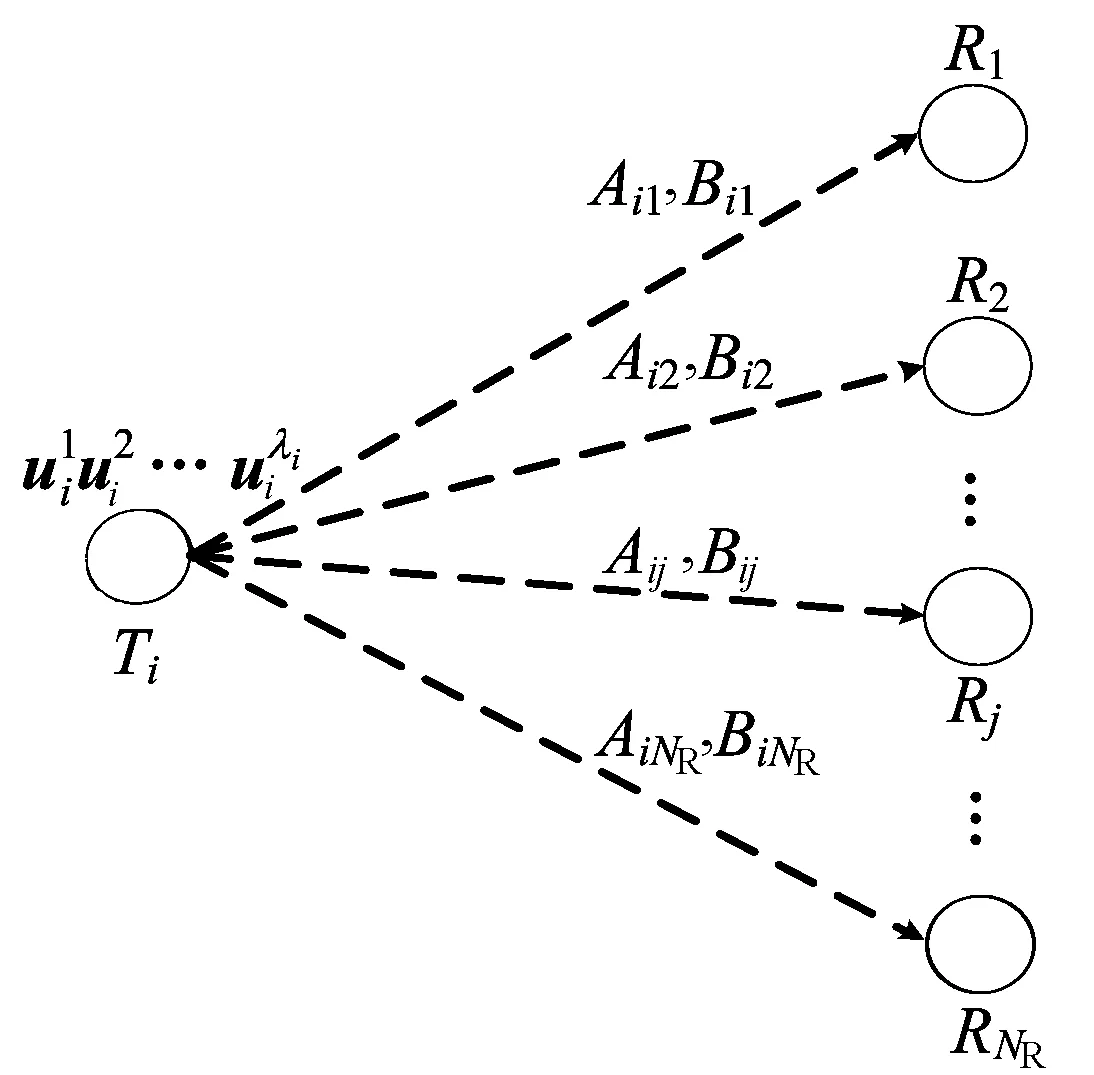
图4 发送节点Ti的IA约束

对于发送节点Ti,基于Aij和Bij的定义,存在Bij⊆Aij,βij≤αij。其中,节点序号i表示节点数,1≤i≤NT。为方便叙述,下面用j表示第j个节点,j∈Li,Li为节点Ti的干扰范围内的节点集合。

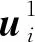
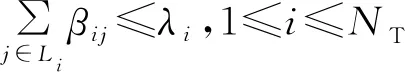
(1)

接收节点的IA约束如图5所示。

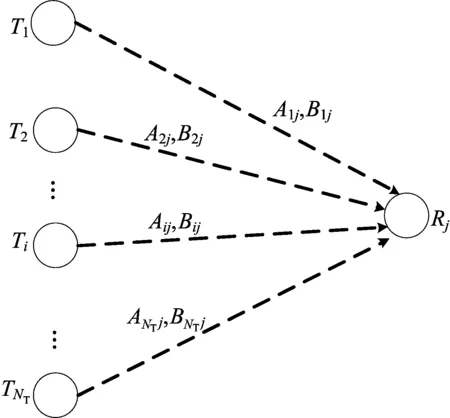
图5 接收节点Rj上的IA约束

对于接收节点Rj,有如下结论:

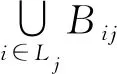
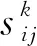
(3) 要确保Bij上任何2个干扰流不能与AijBij上同一个干扰流对齐。则有:

(2)

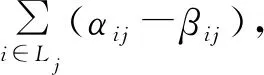
(3)

2.3 干扰对齐算法

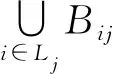
(1) 在发送节点Ti上,从Aij上选择1个子集Yij1或Yij2形成Bij。选择条件为:

Yij1∩Yij2=∅,j1,j2∈Li,j1≠j2, 1≤i≤NT

(4)

若βij满足(1)～(4)式,则可以将其选入Bij,由此确保Bij中的每个干扰流都有一个特定的预编码向量与其相对应。

(2) 在接收节点Rj上,将Bij上的干扰流对齐到Aij其他的干扰流上。令Xij为干扰流Aij的预编码向量集合,令Yij为干扰流Bij的预编码向量集合,则有:

并且存在|Xij|=αij,|Yij|=βij。

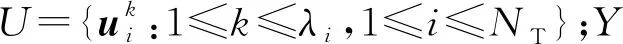
UY中的每个预编码向量可表示为:

(5)

其中,ek为第k个元素为1、其余元素为0的向量。

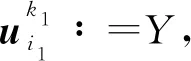
(6)

其中,im≠im+1,m=1,2,…,M-1。

当下列2种情况发生,关系式c0将终止。

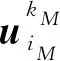
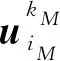
为构建c0中的预编码向量,将c0分为2个子式c1和c2,即

对于c1和c2,首先构造c1中的预编码向量,然后构造c2中的预编码向量。根据c2中构造关系,存在:

⋮

(7)

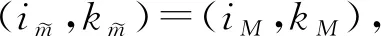
(8)

(7)式、(8)式来自同一个线性方程系统,其中H(固有信道矩阵)是给定的矩阵,u是变量,因此有:

(9)

3 优化模型

3.1 模型约束

在第t个时隙,用变量xi(t)表示第i个节点(i∈N)是否为发送节点,若节点i是发送节点,则xi(t)=1;否则xi(t)=0。同样地,用变量yi(t)表示该节点是否为接收节点,若节点i是接收节点,则yi(t)=1;否则yi(t)=0。由此可知存在:

xi(t)+yi(t)≤1, 1≤i≤N0, 1≤t≤K

(10)

用zl(t)来表示在第t个时隙数据流l上数据流的数目。若节点i是发送节点,则有:

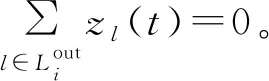
1≤i≤N0, 1≤t≤K

(11)

类似地,通过判断节点i是否为接收节点,存在:

1≤j≤N0, 1≤t≤K

(12)

由2.2节可知,在第t个时隙,若节点i是发送节点,则存在如下3条约束:

βij(t)<αij(t),j∈Li, 1≤i≤N0, 1≤t≤K

(13)

1≤i≤N0, 1≤t≤K

(14)

1≤i≤N0, 1≤t≤K

(15)

由2.2节可知,在第t个时隙,若节点i是接收节点,则存在如下2条约束:

i∈Lj, 1≤j≤N0, 1≤t≤K

(16)

1≤j≤N0, 1≤t≤K

(17)

由2.2节可知,若在第t个时隙,节点i为发送节点,而节点j为接收节点,则存在如下约束:

i∈Lj, 1≤j≤N0, 1≤t≤K

(18)

其中,Rx(l)为接收数据流l的接收节点，且xi(t)=0。显然(18)式是非线性的,此处通过重新线性化技术[10]来线性化(18)式。

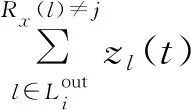
j∈Li, 1≤i≤N0, 1≤t≤K

(19)

0≤αij(t)≤Byi(t),

j∈Li, 1≤i≤N0, 1≤t≤K

(20)

其中,B为固定整数(例如,B=NA)。

3.2 优化模型

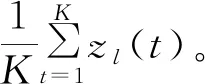
因为聚合数据速率不能超过平均链路速率,所以有:

1≤f≤F0, 1≤l≤L0

(21)

源节点存在遵守流守恒定律,则有:

(22)

其中,i表示第i个节点。

中继节点存在遵守流守恒定律,则有:

1≤i≤N0,i≠s(f),i≠d(f), 1≤f≤F0

(23)

优化目标为数据流在会话中达到最小速率的最大值,用rmin来表示,且有:

rmin≤r(f), 1≤f≤F0

(24)

该优化问题OPT-IA可表达如下:

其中,xi(t)、yi(t)为二进制变量;zi(t)、αij(t)、βij(t)为非负整数变量;r(f)、rl(f)为非负变量;NA、N0、L0、F0、K、B为常数。

优化问题OPT-IA是一个典型混合整数线性规划(mixed-integer linear programming,MILP)问题。MILP的商用求解器CPLEX[14]通常采用B&C来求解MILP模型,并融合了预处理和启发式等多类算法集。本文采用CPLEX求解maxrmin的数值结果。

4 仿真分析

考虑一个随机生成的井下多跳网络,包含20个节点,节点的网络布局如图6所示,分布在1 000 m×350 m矩形区域(由于井下环境是狭长的巷道,属于条带状网络节点)。网络中的每个节点配备8个天线。

图6 节点的网络布局

假设所有节点都具有相同的传输范围(150 m)和干扰范围(300 m)。

网络中存在4个活动会话,即N0到N5,N7到N1,N9到N8,N18到N9。假设一个数据传输过程需要3个时隙,即时隙a、时隙b、时隙c。通过求解OPT-IA,从而获得如下的数值结果。

时隙a、时隙b、时隙c的发送/接收模式、干扰模式和IA情况如图7所示。图7中,带箭头的实线表示预期数据链路,实线上的数字为该数据链路的数据流数目,即zl;带箭头的虚线表示干扰流,虚线上的数据为αij和βij。例如,图7a中N0和N6之间的虚线[2,2]表示α0,6=2和β0,6=2,即表示有2个干扰流从节点N0到节点N6,并且对齐到节点N6上。

仿真结果表明井下多跳网络的吞吐量明显提升。例如,时隙c中的节点N8(参见图7c)。节点N8共有6个干扰流(从发送节点N2、N3及N13)。对于来自节点N2的2个干扰流、来自节点N3的干扰流,均与来自节点N13的干扰流对齐,即节点N8的6个干扰流中的4个已成功与剩下2个干扰流对齐。

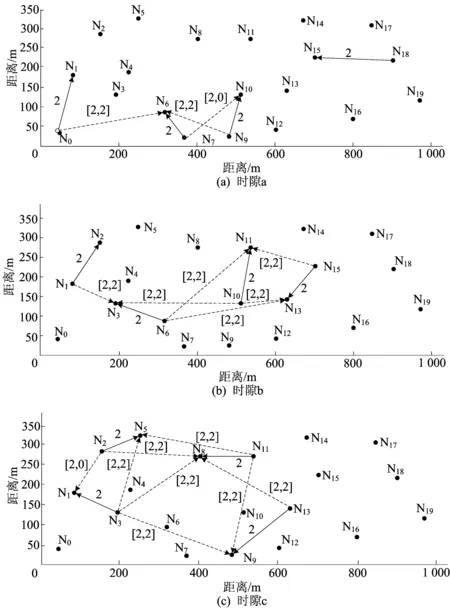
图7 3个时隙的发送/接收模式、干扰模式和IA情况

因此,节点N8只需要消耗2个自由度去消除6个干扰流的干扰。

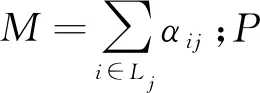
表1 各接收节点自由度消耗情况

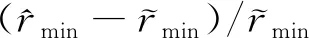
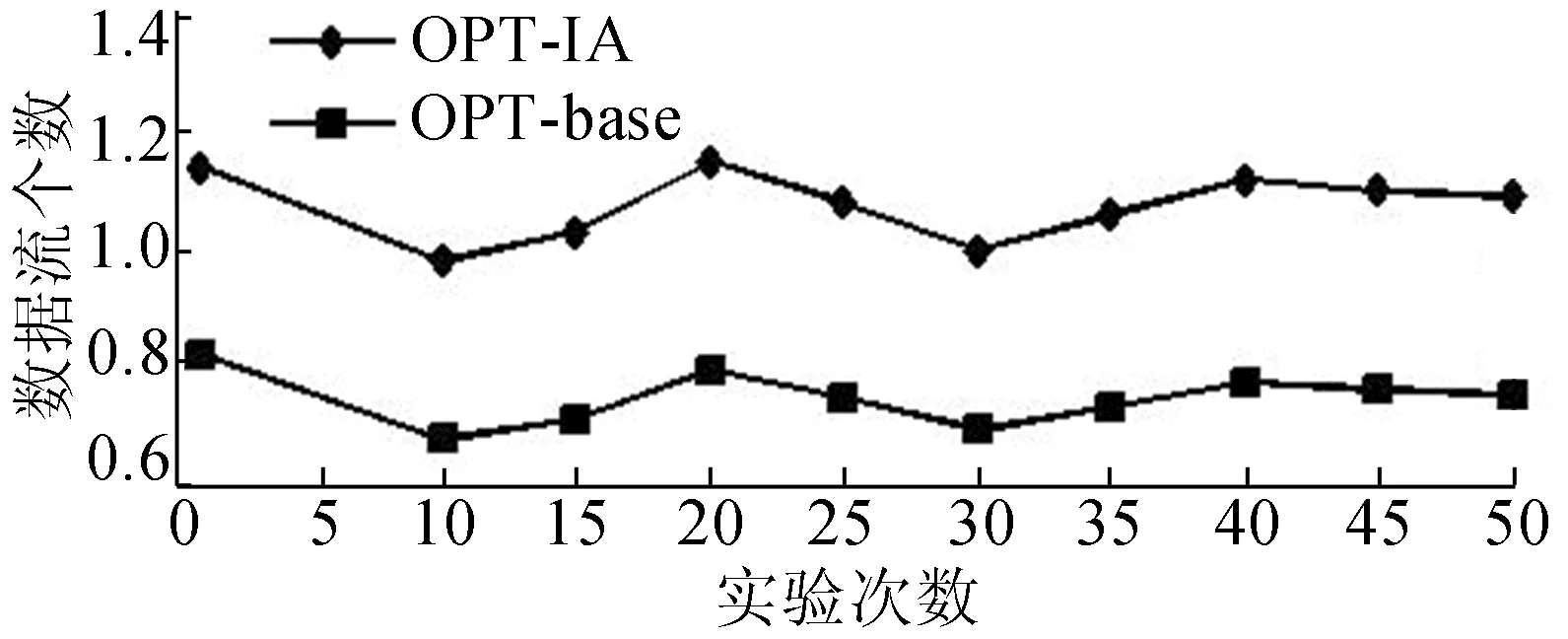
图8 OPT-IA与OPT-base网络速率对比

5 结 论

本文针对井下多跳无线传感网络由于干扰导致节点天线资源利用率不高的问题,提出基于IA机制的系统模型。首先将网络数据传输过程分成若干个时隙,在各个时隙对发送节点和接收节点进行IA约束,并给出预编码向量构建算法;然后以MILP问题刻画优化模型并采用CPLEX解出数值解;最后通过仿真实验验证了算法的可行性和有效性,并进一步得出基于IA的优化算法可提高45%的网络吞吐量。

后续研究将引入多跳路由,并寻求更完备的天线阵列仿真工具。