基于遗传BP神经网络的双目相机手眼标定研究

丁雷鸣, 徐海明, 吕 品,3, 赵丹阳, 严亚飞, 孙丙宇

(1.合肥工业大学 工业与装备技术研究院,安徽 合肥 230009; 2.中国科学院合肥物质科学研究院 智能机械研究所,安徽 合肥 230031; 3.泰安华鲁锻压机床有限公司，山东 泰安 271000)

0 引 言

视觉系统作为果蔬采摘机器人进行环境感知与实现采摘目标识别和定位的关键组成部分,其工作性能的好坏直接决定了机器人能否成功高效采摘[1]。双目立体视觉是一种使用较多的目标识别与定位的方法[2-4]。视觉与机器人关联方式需要确定视觉系统坐标系与机械臂关节坐标系的转换关系,即手眼标定。对于视觉系统与其他坐标系之间的标定方法,近年来很多学者进行了大量的研究。文献[5]采用P3P位姿测量原理获得相应空间点在摄像机坐标系中的坐标,建立了标定方程组,基于最小二乘法标定出了手眼系统之间的转换矩阵;文献[6]通过多元线性回归拟合模型完成了基于双目视觉的采摘机器人手眼标定;文献[7]提出了一种基于三坐标测量仪的高精度手眼标定新方法,利用三坐标测量仪将机器人末端工具、法兰盘、相机构建成闭环系统,具有很强的实用性;文献[8]提出了一种基于误差分布估计的加权最小二乘鲁棒估计方法,在数据粗差影响下保持较高的标定精度。

现有算法通常采用最小二乘估计求解方法对机器人手眼系统的变换参数进行相机坐标系与其他坐标系的线性标定,而未考虑双目视觉系统的非线性系统误差[9]。反向传播(back-propagation,BP)神经网络模型是目前广泛应用的预测模型,具有广泛的工程应用[10-11],其高效的非线性映射能力恰好弥补了传统标定方法未考虑双目视觉系统非线性系统误差的不足。但是BP神经网络模型存在易陷入局部极小值、收敛速度慢等缺点，文献[12]通过引入粒子群算法进行全局搜索来解决该问题;文献[13]通过使用ADAM算法代替传统BP神经网络所使用的随机梯度下降算法BP神经网络，避免因陷入局部最优而导致的预测误差较大的问题。

为了克服上述缺点,本文采用遗传算法优化BP神经网络模型,经过选择、交叉、变异以及种群进化操作优化BP神经网络的初始权值和阈值,克服其收敛速度慢、易陷入局部极小值的缺点。在以双目视觉相机为基础构建的果蔬采摘机器人样机上的实验结果表明:与传统线性回归模型与BP神经网络模型相比,经遗传算法优化后的BP神经网络模型显著地减少了标定误差,更好地表达了相机坐标系之间的关系。

1 线性回归模型

手眼标定是指求取摄像机坐标系与机械手坐标系之间的矩阵变换关系。手眼安装一般有2种形式:① Eye-in-hand系统(摄像机直接安装在机械手上,随机械手一起运动);② Eye-to-hand系统(摄像机固定安装,位置不随机械手运动而改变)。本文系统采用双目摄像机固定安装手眼系统,由于立体视觉模块可以给出靶标在相机坐标系下的三维坐标,该系统标定简化为求解相机坐标系与机器臂坐标系之间的映射矩阵。两坐标系之间的齐次坐标变换关系可写为:

(1)

将(1)式变形为:

(2)

传统方法通过线性回归求解,(2)式只有参数矩阵的秩和未知参数个数相等时才可以求解,即最少需要4个线性无关的点才能求解R、T,将n(n≥4)个点坐标代入(2)式,其求解实际上转换为最小二乘问题,此时R的解可用最小二乘法求得,即

R=(ATA)-1ATB

(3)

以上为传统线性回归模型标定固定双目视觉手眼系统的原理。

2 BP神经网络模型

1986年,由斯坦福大学的Rumelhart D E等提出的BP神经网络算法解决了多层网络模型中隐含层的连接权问题,有效提升了神经网络的自学习和组织能力,是当前工程领域应用较多的一种前馈式学习算法与反向传播算法的神经网络。BP神经网络的输入层由隐含层作用于输出层,经非线性变换得输出量。网络训练的每个样本包含输入量和期望输出量,网络输出量与期望输出量之间的偏差通过调整网络权值与阈值使误差沿梯度方向下降,直至实际输出与期望输出在预定范围内。

设输出层有m个神经元,BP网络的实际输出是y,期望输出是y′,函数ε为:

(4)

每个权值的修正值为:

(5)

其中,ωij为输入单元i到第j个隐含层的权重;η为学习速率;fj为中间第j个隐含层的传输函数。输入层到隐含层的函数采用logsig型,隐含层到输出层的函数采用purelin型。

将靶标在相机坐标系下的坐标Xc、Yc、Zc作为网络的输入,选取靶标在机械臂坐标系下相应的坐标Xr、Yr、Zr为输出,建立BP神经网络模型。BP神经网络的隐含层节点数对BP神经网络预测精度有较大的影响。节点数太少,网络学习效率低,需要增加训练次数,训练精度也受到影响;节点数太多,网络容易过拟合。最佳隐含层节点数可参考如下公式[14],即

(6)

其中,n为输入层节点数;l为隐含层节点数;a为0～10之间的常数。

经实验选择隐含层节点数为10个。据此,该BP网络模型采用3层网络,BP 神经网络结构为3-10-3。

在训练BP神经网络前,为减弱各不同量级的坐标值对网络模型训练的影响,先对坐标值作归一化处理。

3 遗传算法优化BP神经网络模型

遗传算法擅长全局搜索,BP神经网络用于局部搜索较有效,因此将遗传算法和BP算法相结合。遗传算法对神经网络初始权值进行优化,定位出较好的搜索空间,再采用 BP 算法在小空间内搜索最优值。遗传BP神经网络算法流程[15]如图1所示。

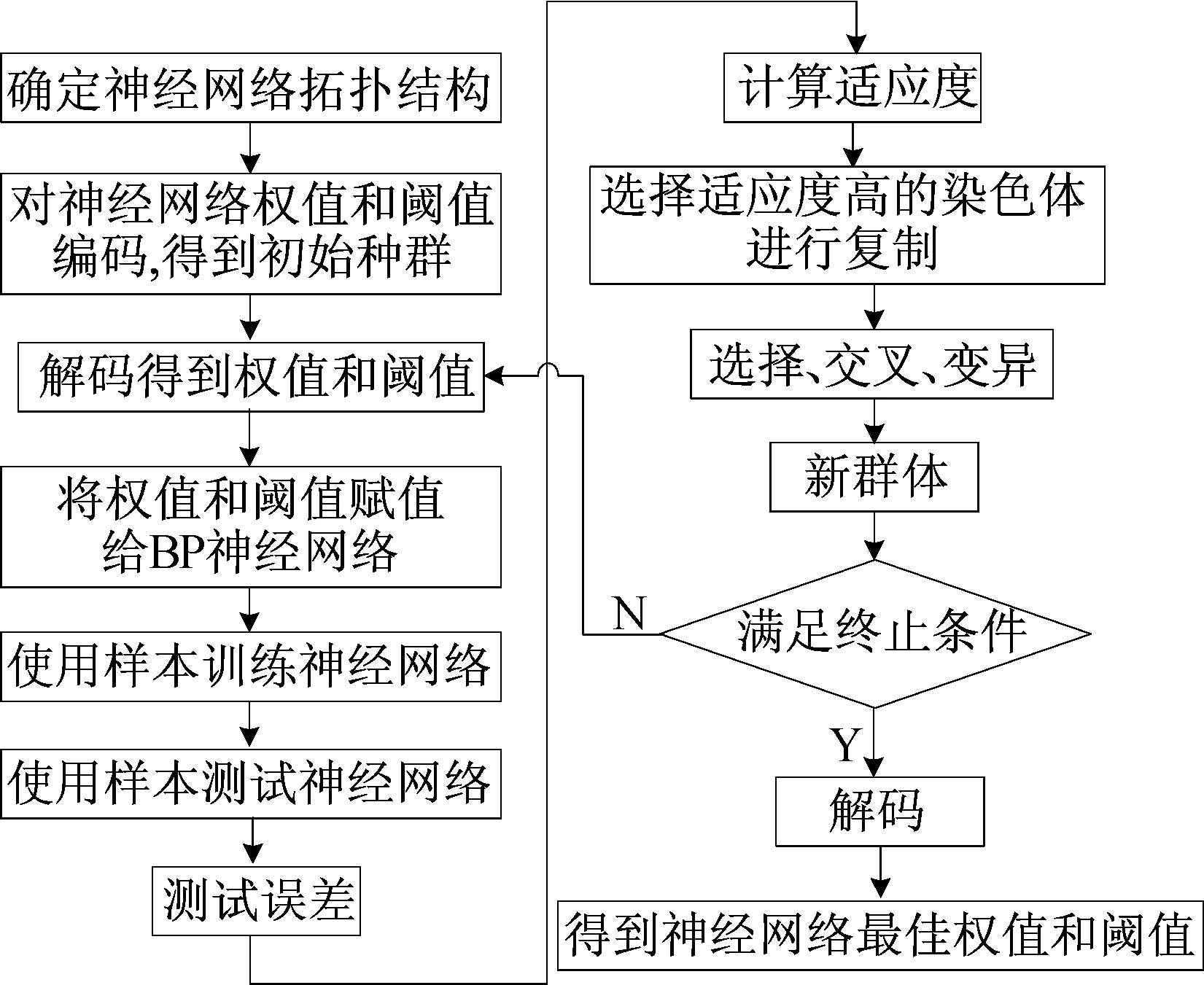
图1 遗传BP神经网络算法流程

改进后的遗传算法具体步骤如下所述。

(1) 初始化种群。随机产生一种群Xm×n,每个个体X1×n均为一个实数串,代表一组神经网络的权值和阈值，包括输入层与隐含层连接权值、隐含层阈值,隐含层与输出层连接权值、输出层阈值4个部分,即

n=rs1+s1s2+s1+s2

(7)

其中,n为个体的长度;r为输入层节点个数;s1为隐藏层节点个数;s2为输出层节点个数。

(2) 适应度函数。由个体到BP神经网络的权值和阈值,依据适应度函数值对其进行评价。计算输出误差值E、适应度函数f,即

f=1/(1+E)

(8)

计算各个体的适应值,种群个体适应度最大者进入子种群。

(3) 选择操作。遗传算法选择操作有轮盘赌法、锦标赛等多种方法,现采用轮盘赌法,即基于适应度比例选择策略,每个个体i的选择概率pi为:

(9)

其中,fi为个体i的适应度函数;N为种群规模,N=50。

(4) 交叉操作。因为采用实数编码,所以交叉操作方法采用实数交叉法,第k个染色体ak和第l个染色体在j位的交叉操作方法如下:

(10)

其中，b为[0,1]区间的随机数。

(5) 选取第i个个体的第j个基因aij进行变异,变异操作方法如下:

(11)

其中,amax为基因aij的上界;amin为基因aij的下界;f(g)=r2(1-g/Gmax)2,r2为一随机数,g为当前迭代次数,Gmax为最大进化次数;r为[0,1]区间的随机数。

4 实验方法与结果分析

4.1 实验方法

采摘机器人样机系统如图2所示,其中相机型号为Bumbelee2双目相机,使用IEEE-1394线与计算机连接；机械臂为ABB六自由度机械臂,重复定位精度为0.02 mm。

图2 采摘机器人样机

首先在机械臂末端执行器上贴上靶标,使机械臂末端运动到指定坐标点,然后双目相机拍摄图片,处理后得到靶标在相机坐标系下的坐标,与机械臂坐标系下的坐标组成一组对应坐标。重复此过程得到94组坐标值，作为网络学习样本。

按照上述实验流程依次得到靶标在2个坐标系下的多组坐标值。为降低实验数据的随机误差,各实验样本组尽量选取线性无关的点。以相机坐标系下的坐标值Xc、Yc、Zc作为网络的输入,选取靶标在机械臂坐标系下相应的坐标Xr、Yr、Zr为输出,得到94组数据,部分样本数据见表1所列。

以表1中94组数据作为BP神经网络的测试样本。首先将网络学习样本数据归一化到[-1,1],再经过多次迭代,使实验数据的网络训练误差值逐步收敛。

表1 手眼标定部分样本数据

4.2 结果分析

遗传算法通过随机问题假设集合,根据适应度函数对个体进行数值评价,遗传算子模拟遗传过程中出现的复制、交叉和变异现象对种群个体择优；遗传算法对BP网络初始权值和阈值进行优化赋值,再利用BP神经网络预测模型局部寻优；遗传算法进化过程中设置种群数为40,进化代数为50,交叉概率为0.7,变异概率为0.01。上述遗传BP神经网络模型用Matlab软件编程实现。遗传进化过程中误差变化曲线如图3所示。由图3可知,个体进化到43代后适应度和误差平方和基本没有变化,可见遗传算法在改善BP神经网络的收敛速度和误差精度方面效果突出。

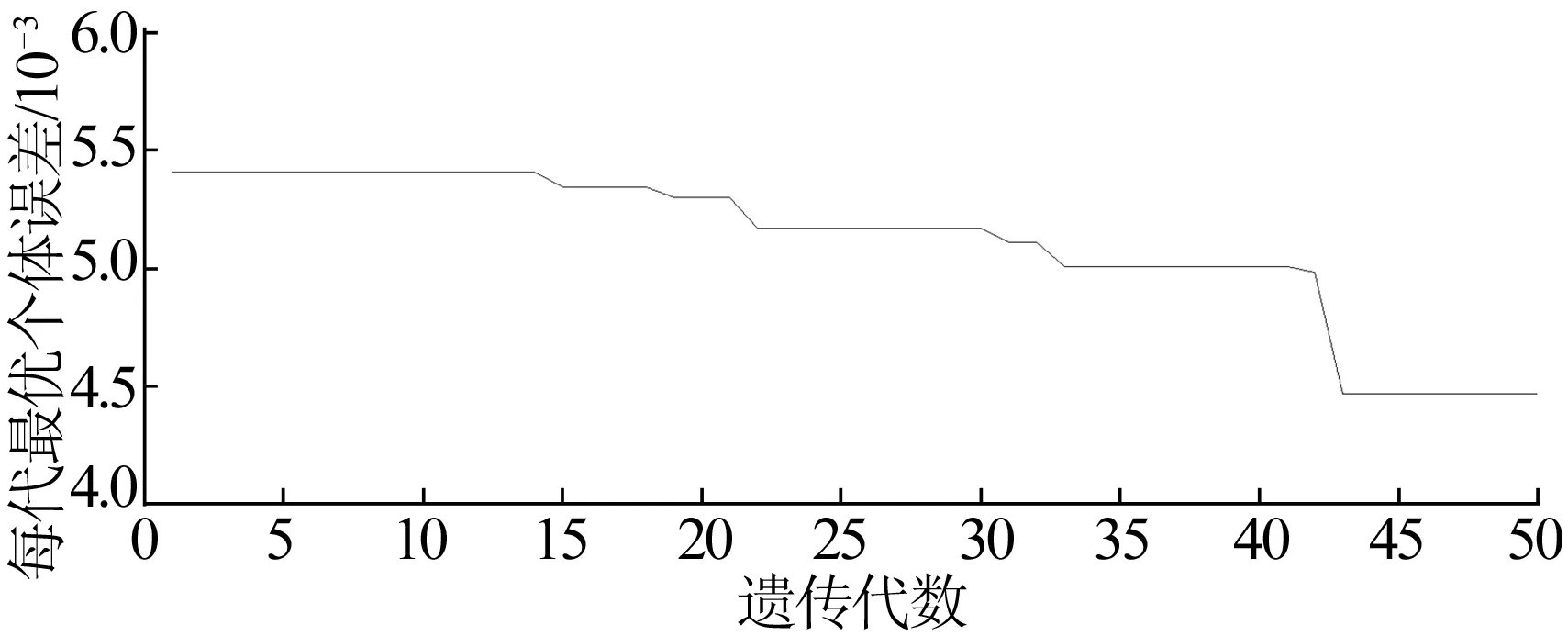
图3 每代最优个体误差变化曲线

遗传BP神经网络预测数据反归一化后与传统的最小二乘法标定的94组样本距离绝对误差比较如图4所示。采用均方根误差MSE和绝对误差MAE 2个特征指标对遗传BP神经网络、BP神经网络、线性回归3种模型进行比较,各类指标值越大预测值与实测值的偏差越大，各统计指标结果见表2所列。由表2可知,经遗传法优化的BP神经网络模型的拟合效果要优于BP神经网络模型和线性回归模型。

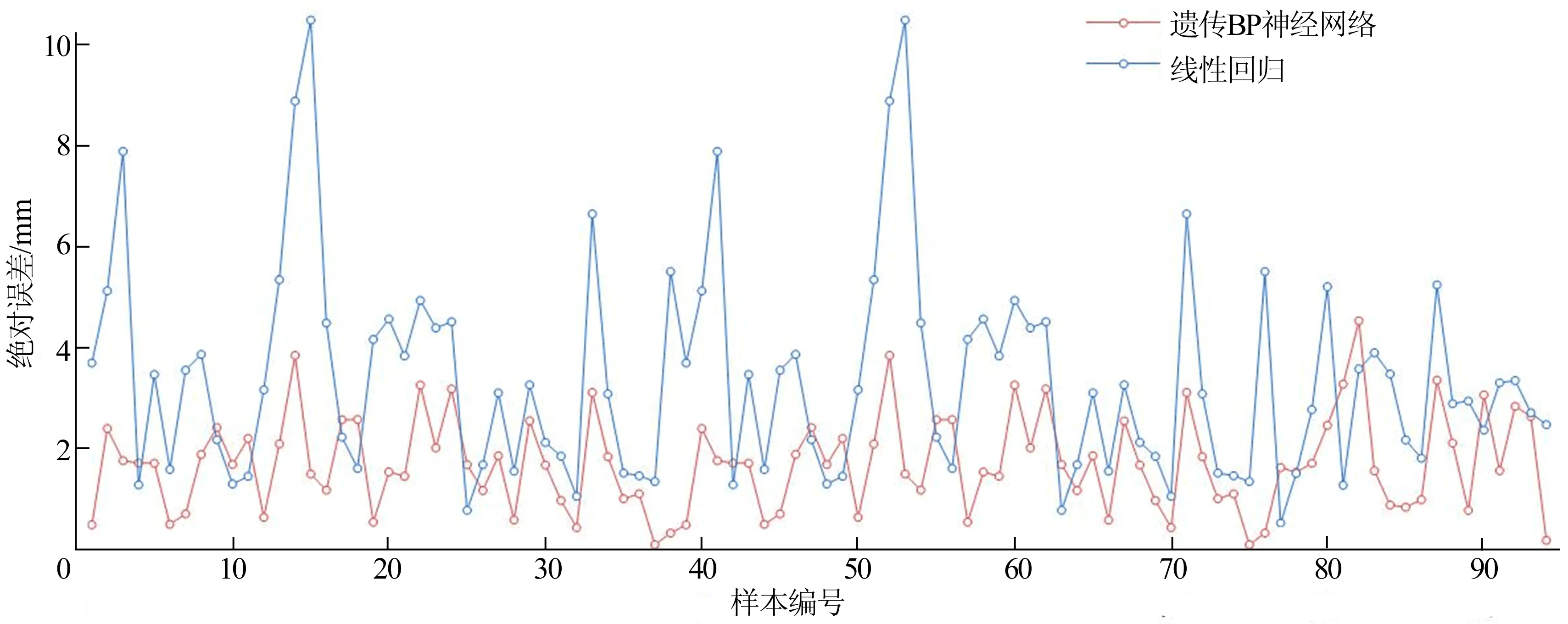
图4 2种模型绝对误差

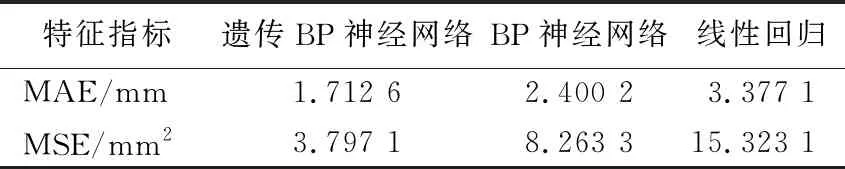
表2 3种模型结果的比较

为检验3种模型标定效果,设计了验证实验。用双目相机拍摄目标果实照片,并读取其在摄像机坐标系下的三维坐标；经上述已建立的3种标定模型将摄像机坐标转换为机械臂坐标；将机械臂坐标输送到机械臂作为靶标定位坐标,双目相机测量靶标与目标果实的距离即标定误差。为降低试验数据的随机误差,每次实验目标果实放置不同位置,重复8次。

实验结果见表3所列。

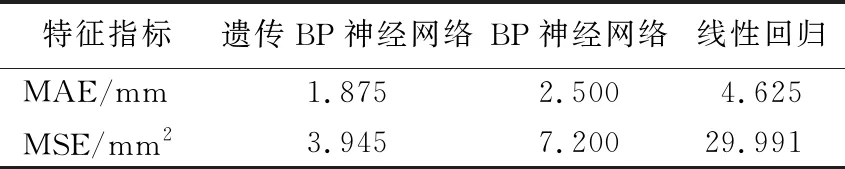
表3 3种模型验证实验结果

5 结 论

本文针对线性回归模型不能消除双目视觉系统非线性系统误差的缺点,建立了BP神经网络,考虑到BP神经网络预测易陷入局部极小值和收敛速度慢的缺点,将遗传算法引入到BP神经网络模型中,经过选择、交叉、变异以及种群进化操作优化BP神经网络的初始权值和阈值,提出了基于遗传BP神经网络的双目相机标定方法。通过实验对比了本文方法、BP神经网络、线性回归3种模型,结果表明，本文方法提高了收敛速度,克服了陷入局部极小值的缺点,达到了很好的标定精度。