基于PSO的无人艇操纵响应模型参数辨识结果优化*

2020-10-19褚式新茅云生董早鹏兰继雷

武汉理工大学学报（交通科学与工程版） 2020年5期

褚式新茅云生董早鹏兰继雷姜昊

(武汉理工大学交通学院武汉 430063)

0 引言

无人水面艇(unmanned surface vessel，USV)的智能化基础是基于对其操纵运动的控制，而USV的操纵运动的预报由其运动数学模型所决定的[1].USV的操纵预报精度直接取决于建立的运动数学模型中的参数获取精度[2].

随着系统辨识学科的发展，辨识逐渐成为学者们获取模型参数的一种重要途径，Abkowitz[3]最早将辨识用于船舶操纵性研究，取得了非常好的效果，改变了以往通过实验获取参数的现状，节约了成本.如今辨识算法也越来越智能化，Dong等[4]采用了扩展卡尔曼滤波算法及支持向量机两种算法辨识了USV的二阶非线性响应模型，获取了模型参数，并对比了获取的模型参数对USV操纵性的预报精度的影响，发现扩展卡尔曼滤波算法在辨识精度上优于支持向量机；罗伟林等[5]对支持向量机算法进行了改进，提出了最小二乘支持向量机辨识船舶的操纵运动模型，并采用仿真实验验证了算法的有效性；随着神经网络的兴起，有学者利用神经网络强大的学习与自适应能力，与系统辨识相结合，提出了利用神经网络辨识船舶操纵运动模型的水动力导数的算法，并进行了对应的操纵实验验证了辨识结果的精确性[6]；递推最小二乘法(recursive least squares，RLS)是目前系统辨识中常用的一种算法，是基于最小二乘法辨识结果所进行的一种改进的在线辨识算法[7]，但是RLS算法辨识精度往往依赖于数据量，大部分通过辨识得到的模型参数精度均有待提升，需要对结果进一步优化，粒子群(particle swarm optimization，PSO)算法是诸多智能优化算法中效果比较好的一种算法，具有极强的全局搜索能力[8]，文中基于USV二阶非线性响应模型，采用RLS辨识算法结合PSO优化算法展开研究.

1 无人艇操纵性响应模型

目前关于USV操纵运动的数学模型分为三种:①以美国Abkowitz教授为代表的整体型建模流派，主要思想是将船体黏性力、桨力与舵力看作一个整体，将其合力以泰勒展开的形式给出；②以日本操纵建模小组(manoeuvring model group)提出的MMG模型，主要思想是将作用于船体的黏性力、桨力与舵力分开计算，并考虑它们的耦合作用；③日本的野本谦作教授利用类比建模法建立的一阶响应模型，主要思想是将模型简化，只考虑输入舵角与输出首向角的响应关系，故也称为操纵响应模型，后续又发展了二阶非线性响应模型，根据后续发展需求，在方程中又加入了非线性项，见式(1).因模型数学表达简单，故在USV操纵性的研究上应用较为广泛，本文的研究基于此模型展开.

(1)

式中：T1,T2,T3为时间常数，表示USV的应舵性和航向稳定性；K为舵角增益；α为高阶非线性项系数；r为转首角速度；δr为压舵角.

2 基于RLS算法参数辨识

2.1 辨识算法设计

对于一个线性系统，为

Y=Hθ

(2)

式中：Y为系统输出矩阵；H为系统输入矩阵；θ为系统参数矩阵.最小二乘法的辨识准则是使系统中每个观测值与估计值的误差的平方和达到最小，为

J=∑ε2

(3)

式中：ε为误差矩阵，定义为

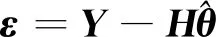
(4)

将式(4)代入式(3)中，对参数矩阵求导为0，得到

(5)

解得

(6)

式(6)即为最小二乘法的辨识结果，但由于最小二乘是一种离线辨识，其辨识效率低且辨识精度非常依赖于数据量的大小，故有学者基于最小二乘的辨识结果进行了一些变换，得到了一系列递推公式，使最小二乘法的辨识结果对数据的依赖程度不高，得到了RLS算法，其主要变换过程如下，设：

[P-1(t-1)+H(t)TH(T)]-1

(7)

式中：Ht为所有时刻的系统输入矩阵;H(t)为t时刻的系统输入矩阵.其次设定误差增益矩阵为

K(t)=P(t-1)H(t)T[I+H(t)P(t-1)H(t)T]-1

(8)

综合式(6)～式(8)，可得到RLS算法的主要递推公式：

P(t)=[I-K(t)H(t)]P(t-1)

(9)

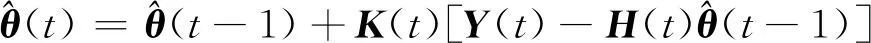
(10)

式(10)即为RLS算法对于线性系统的辨识结果，其辨识结果是依据当前时刻系统的输入和输出值对上一时刻参数辨识值的修正，当参数辨识值变化较为平缓时，即为RLS算法的辨识值.

2.2 数据采集

为采集辨识所需实验数据，选取文献[9]中某USV响应模型参数(见表1)，基于四阶龙格-库塔(Runge-Kutta)进行数值仿真实验，因Z形实验能体现USV良好的操纵性，在Matlab平台进行20°Z形仿真实验，见图1.

表1 某USV响应模型参数

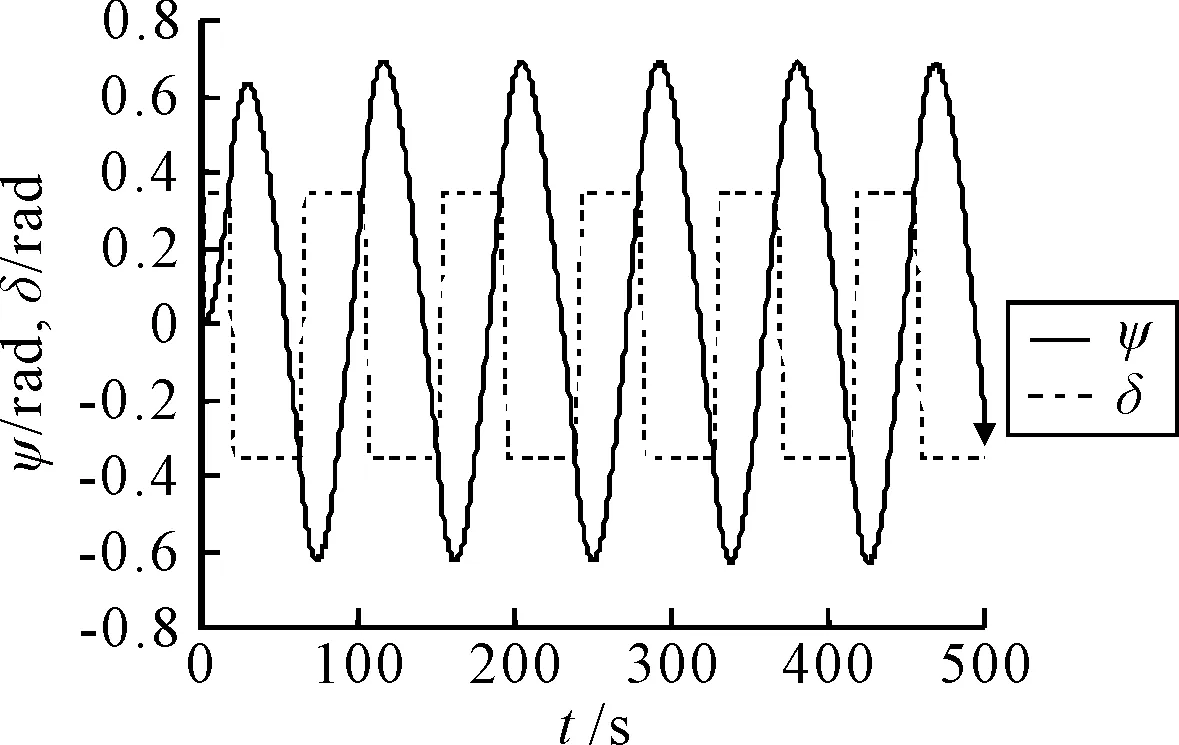
图1 20° Z形仿真实验图

仿真总时间为500 s，时间间隔为0.5 s，采集了舵角δ、首向角ψ等数据，用以开展后续辨识.

2.3 辨识模型设计

由于操纵响应模型式(2)是一个连续的模型，通过仿真实验采集的数据是离散化的，所以需要将辨识模型离散化.在实际实验中，首向角的采集比其他物理量更为容易，故采用欧拉差分法将角速度等物理量差分到首向角，具体差分过程为

(11)

(12)

(13)

(14)

式中：h为时间间隔.

将差分结果带入辨识模型中，令y(t)=ψ(t+1)-ψ(t)，得

y(t+2)-2y(t+1)+y(t)=

(15)

得到形如式(2)的形式，其中输出矩阵为

Yt=[y(t+2)-2y(t+1)+y(t)]

(16)

输入矩阵为

Ht=[δ(t)h3h3h3(δ(t+1)-δ(t))-

h(y(t+1)-y(t))-h2y(t)-y(t)3]

(17)

参数矩阵为

(18)

2.4 参数辨识结果

基于2.3设计的辨识模型，结合2.2的仿真数据，可得到各个时刻的系统输入输出矩阵的值，在RLS算法的递推公式下，可得到每时刻的参数估计值，见图2.

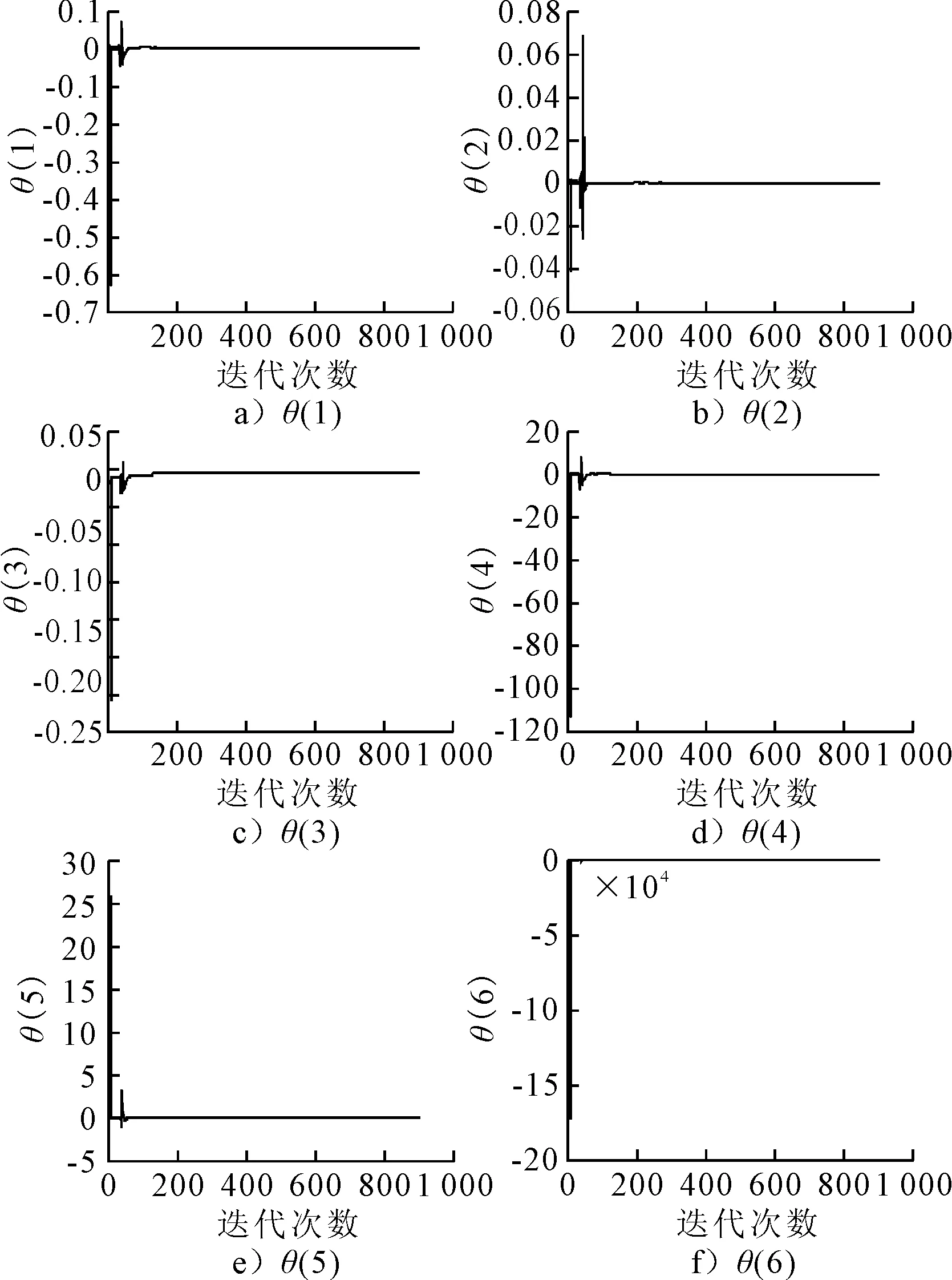
图2 RLS辨识结果图

当其辨识结果收敛时，其收敛值即为RLS算法的参数辨识值，其收敛值见表2.

表2 RLS算法辨识收敛值

基于参数矩阵中各参数的表达式，依次解方程可得到USV操纵响应模型的参数辨识值，见表3，且由辨识结果可知，T1,K,δr辨识精度较高，T2,T3,α辨识精度较差，为更为精确的预报无人艇的操纵性，需要对辨识精度进一步优化.

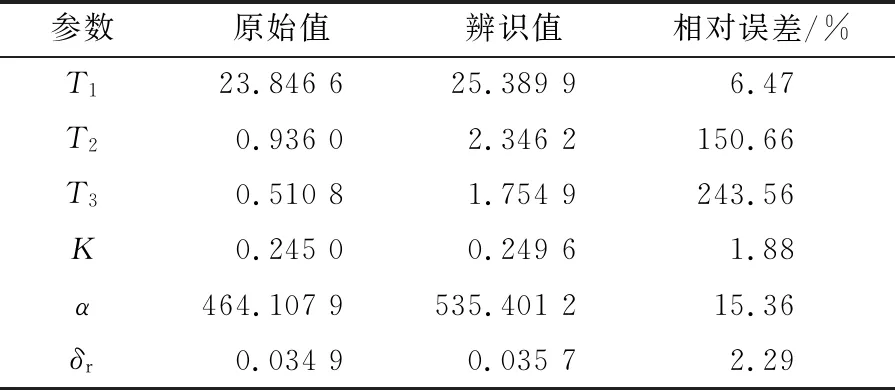
表3 RLS算法辨识值

2.5 基于PSO算法对辨识结果的优化

通过RLS算法辨识结果设定PSO算法寻优的范围，设定iden=[T1,T2,T3,K,α,δr]为辨识值，A为限制矩阵，则PSO寻优范围上限为Xmax=iden+iden×A，下限为Xmin=iden-iden×A，式中：

(19)

初始粒子群设定为1 000个粒子组成的种群，每一个粒子表示为一个潜在解，为

X=(X1,X2,X3,…,X1 000)

(20)

其次初始化粒子速度，设定Vmax=0.001，Vmin=-0.001，速度表示为

V=(V1,V2,V3,…,V1 000)

(21)

设定适应度函数为

fitness=∑(Y-Ye)2

(22)

式中：Y为实际系统输出；Ye为基于粒子值所估计的系统输出，由于Z形实验舵角变化较为单一，将采用20°正弦实验数据进行优化，仿真数据见图3.

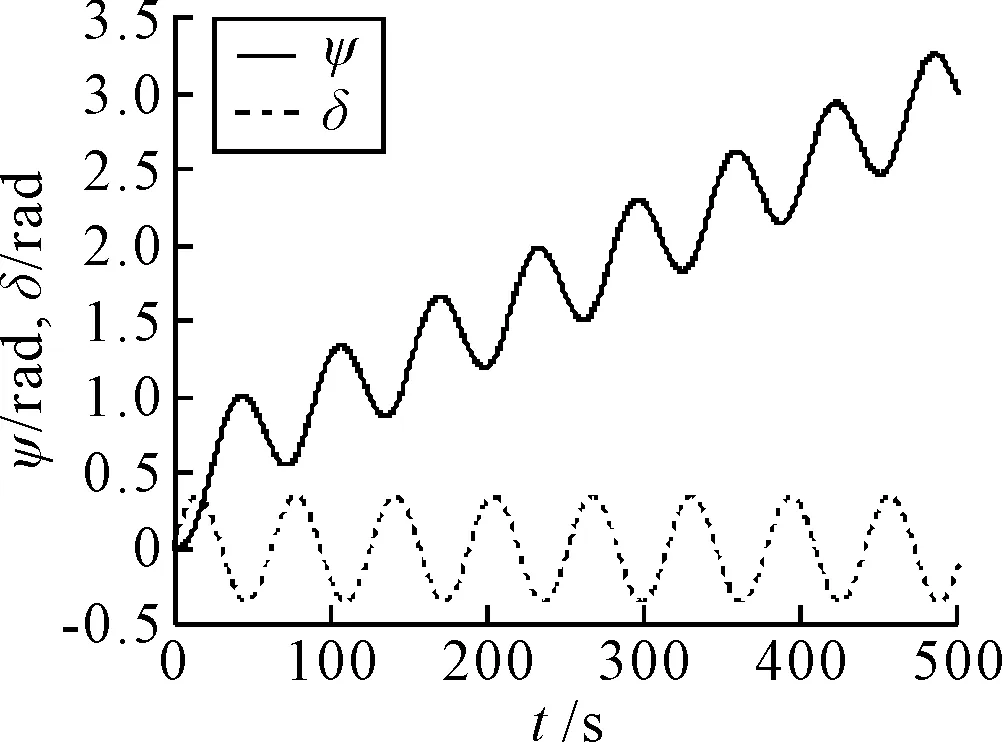
图3 20°正弦仿真实验

计算每个粒子的适应度函数值，基于粒子的适应度函数值找出粒子的个体极值pbest和群体极值gbest，然后对粒子进行速度和位置的更新，更新方法为

vi,j(t+1)=ωvi,j(t)+c1r1[pbest-xi,j(t)]+

c2r2[gbest-xi,j(t)]

(23)

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(24)

式中：i为粒子数；j为该粒子中的变量数；ω为惯性权重系数，设为0.729 8；c1,c2为学习因子，设定为c1=c2=2；r1,r2为0～1之间均匀分布的随机数.

当粒子的速度与位置更新后，重新计算适应度函数值，依据新的适应度函数值跟新粒子群的个体极值pbest和群体极值gbest，当粒子到达最优解时或者达到最大迭代代数时停止更新，一般设定最大迭代代数为100，基于Matlab平台得到的粒子群优化操纵响应模型参数的适应度函数值变化曲线见图4.

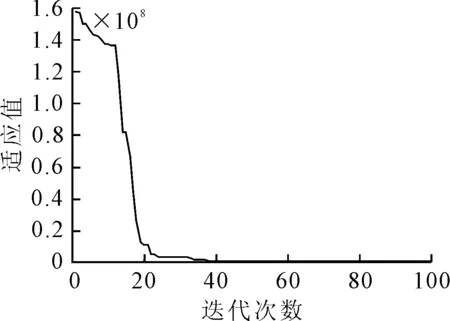
图4 PSO算法适应度值变化图

由图4可知，在迭代到60代时，适应度函数值基本趋向为一个接近0的小值，此时得到的结果为优化结果，将优化结果与RLS算法辨识结果相比较，见表4.由表4可知，基于PSO优化的参数结果比只用RLS算法辨识的参数结果要更精确，其中因T1,K,δr辨识精度较高，所以优化精度提升较小；而T2,T3,α参数因辨识精度较差，所以在优化过程中得到了较大提升.综上，基于PSO算法能有效的优化操纵响应模型参数辨识结果，提升辨识精度.

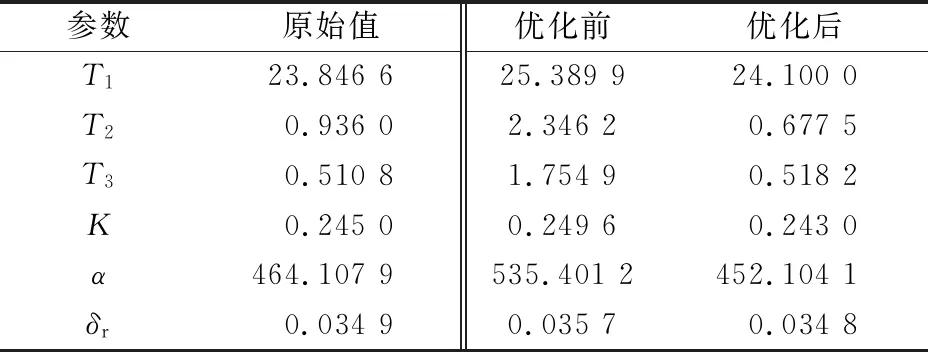
表4 PSO优化结果对比

3 仿真实验

为验证USV操纵响应模型参数辨识结果的精确度，将开展10°,20°及30°Z形、正弦,以及回转等标准操纵运动仿真实验验证辨识结果对操纵性预报的影响，基于表4的优化结果与辨识结果相对比，因在实际实验中，首向角较为容易观测，故在图中只显示了首向角的对比，实验结果见图5.

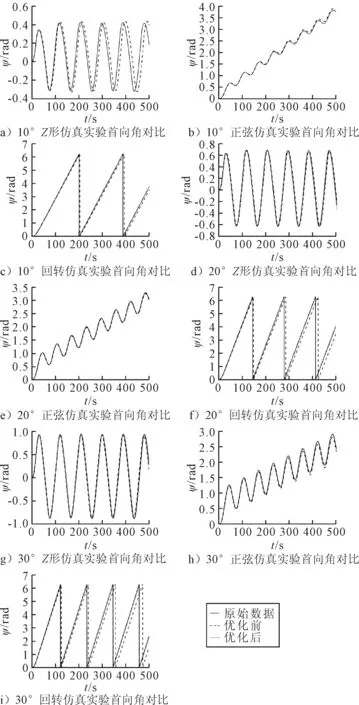
图5 操纵运动仿真实验图

由图5可知，基于PSO优化的各个参数的结果在仿真实验中的首向角变化均比优化前更接近实际变化，即优化后的辨识结果能更精确的预报USV的操纵性，其次基于PSO优化的结果在各种操纵仿真实验下均对USV操纵性的预报有一定提升，说明基于PSO算法优化的参数辨识结果也具有很强的泛化性.综上，基于RLS算法能有效的辨识USV二阶非线性操纵响应模型，且其辨识值具有一定的精度，基于辨识结果，采用PSO智能算法对其进行优化，其优化结果能提升RLS算法的辨识精度，使其辨识结果能有效的预报各种USV操纵运动.