基于裂缝分布的开裂钢筋混凝土梁抗弯刚度计算*
2020-10-19王雨阳付春雨
朱 胤 王雨阳 付春雨
(河海大学土木与交通学院 南京 210098)
0 引 言
由于混凝土抗拉强度低,极易产生裂缝,裂缝会通过混凝土内部应力重分布,削弱混凝土与钢筋之间的黏结等因素来降低钢筋混凝土梁抗弯刚度,进而影响了混凝土梁的耐久性.
众多学者基于黏结滑移理论,分析钢筋与混凝土的应力-应变,得出开裂梁抗弯刚度计算方法.Castel等[1-2]假设了钢筋与混凝土的应变在黏结滑移传递长度内的分布函数及横截面处的应力分布模式,给出了宏观单元内平均惯性矩的表达式.Teng等[3]在Castel的基础之上,计入微裂缝对钢筋与混凝土黏结的损伤,提出更加精细化的模型.Kwak等[4]提出钢筋混凝土拉伸试件中钢筋与混凝土的应变多项式分布函数并推广至受弯构件中,给出受弯构件有效受拉截面面积的计算方法及截面内力的分布状况,以计算开裂钢筋混凝土受弯构件的刚度.这些模型可用于估算设计阶段的梁刚度,但不考虑实际钢筋布置和裂缝分布.因此,这种模型不适用于使用阶段的裂缝分布不规则的既有混凝土梁刚度计算.
文中将裂缝的深度和位置作为开裂梁抗弯刚度计算的考虑因素,根据裂缝对截面应力分布的影响程度选取关键截面并提出不同的截面正应变非线性分布模型,通过内力平衡方程求解分布模型中的未知量,进而得出截面的内力分布.在此基础上对各个截面惯性矩进行精确计算,用来评估已有开裂梁的抗弯刚度.
1 开裂钢筋混凝土梁刚度计算方法
以开裂钢筋混凝土简支梁为研究对象,得出裂缝影响区域内的刚度计算方法.结构的布置简图见图1,简支梁跨径为L,梁高为h,梁宽为b,裂缝深度为dc,裂缝至支座A的轴向距离为lc.梁体内配置有直径为φ的变形钢筋,钢筋的数量为ns,钢筋形心至梁底部的距离为as,集中力P0距离支座的距离为lp.为了得到梁的精确的刚度,首先根据裂缝对梁的贡献大小不同将裂缝附近的梁划分不同的区域,然后针对不同的区域进行钢筋-混凝土的黏结损伤和非线性混凝土应变分布的模拟,根据裂缝对梁的贡献将裂缝附近梁划分成不同的区域,并在此基础上计算截面惯性矩和梁的刚度.

图1 结构整体布置图
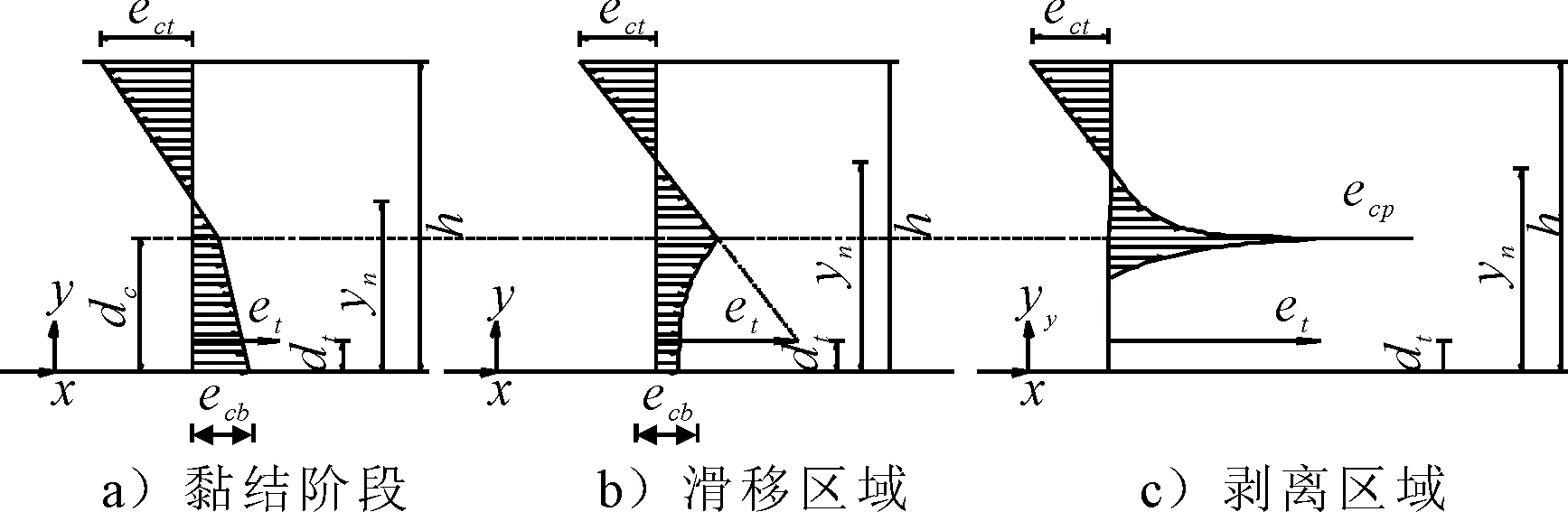
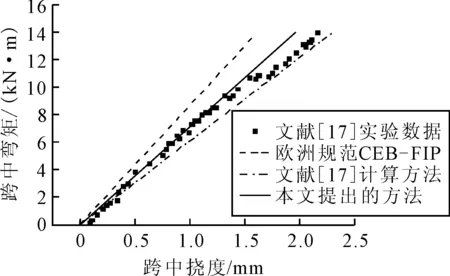
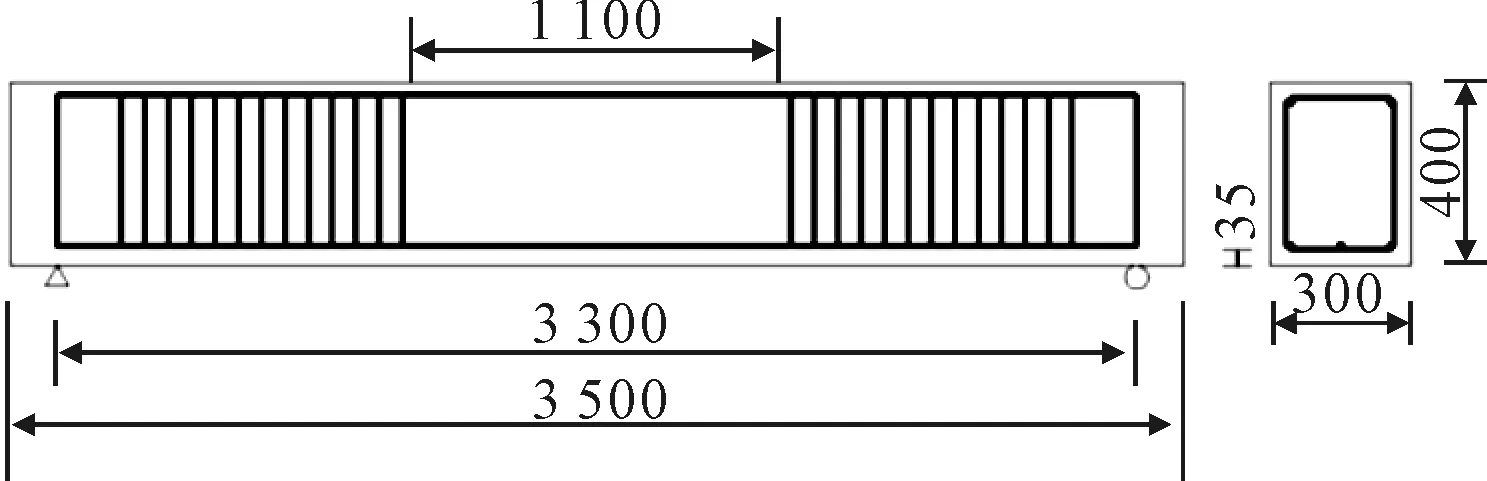
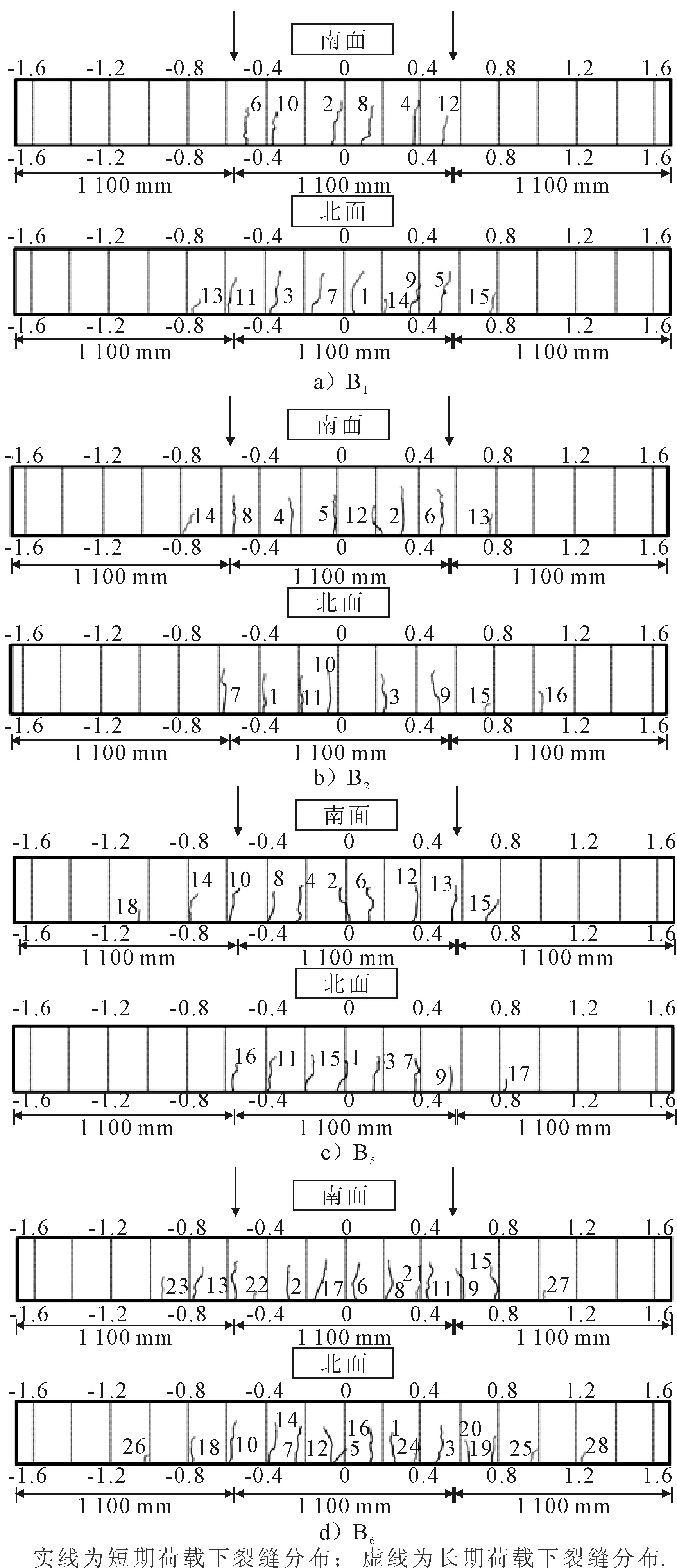
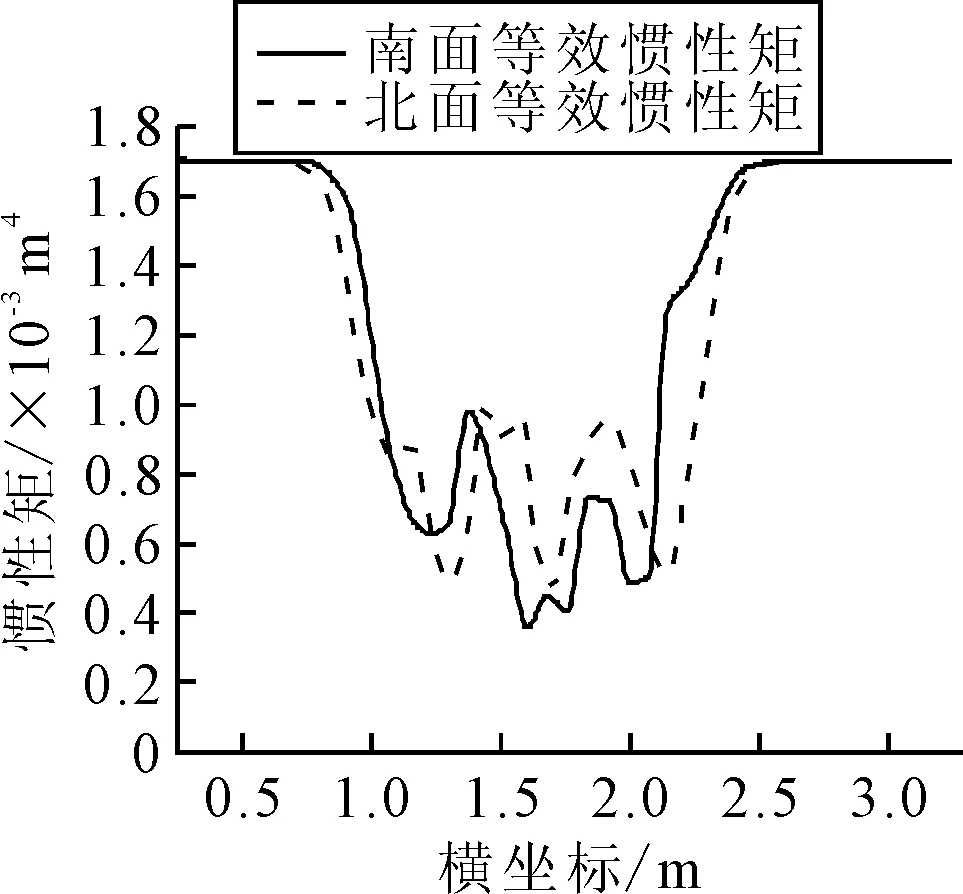
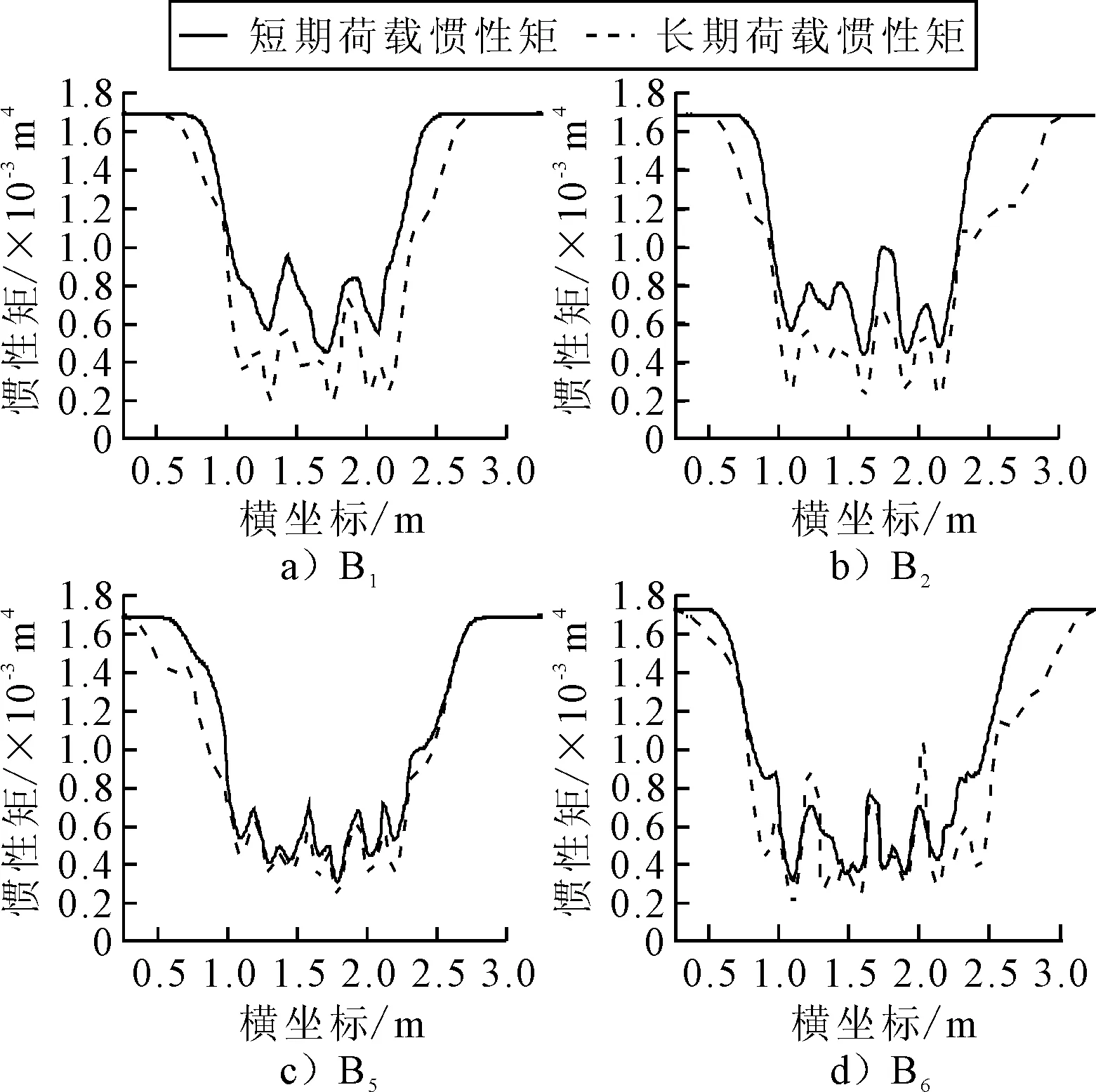
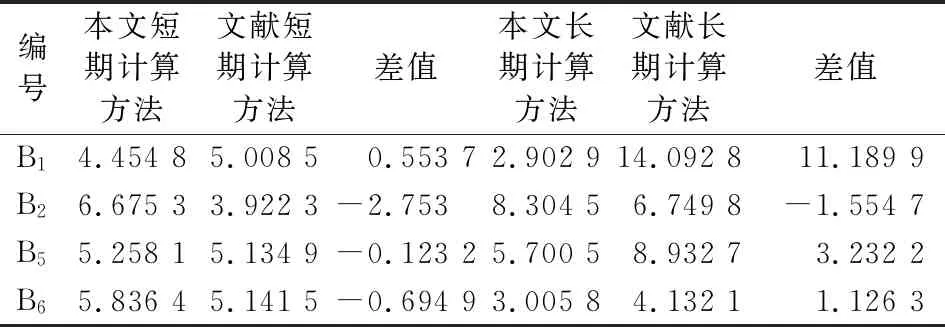
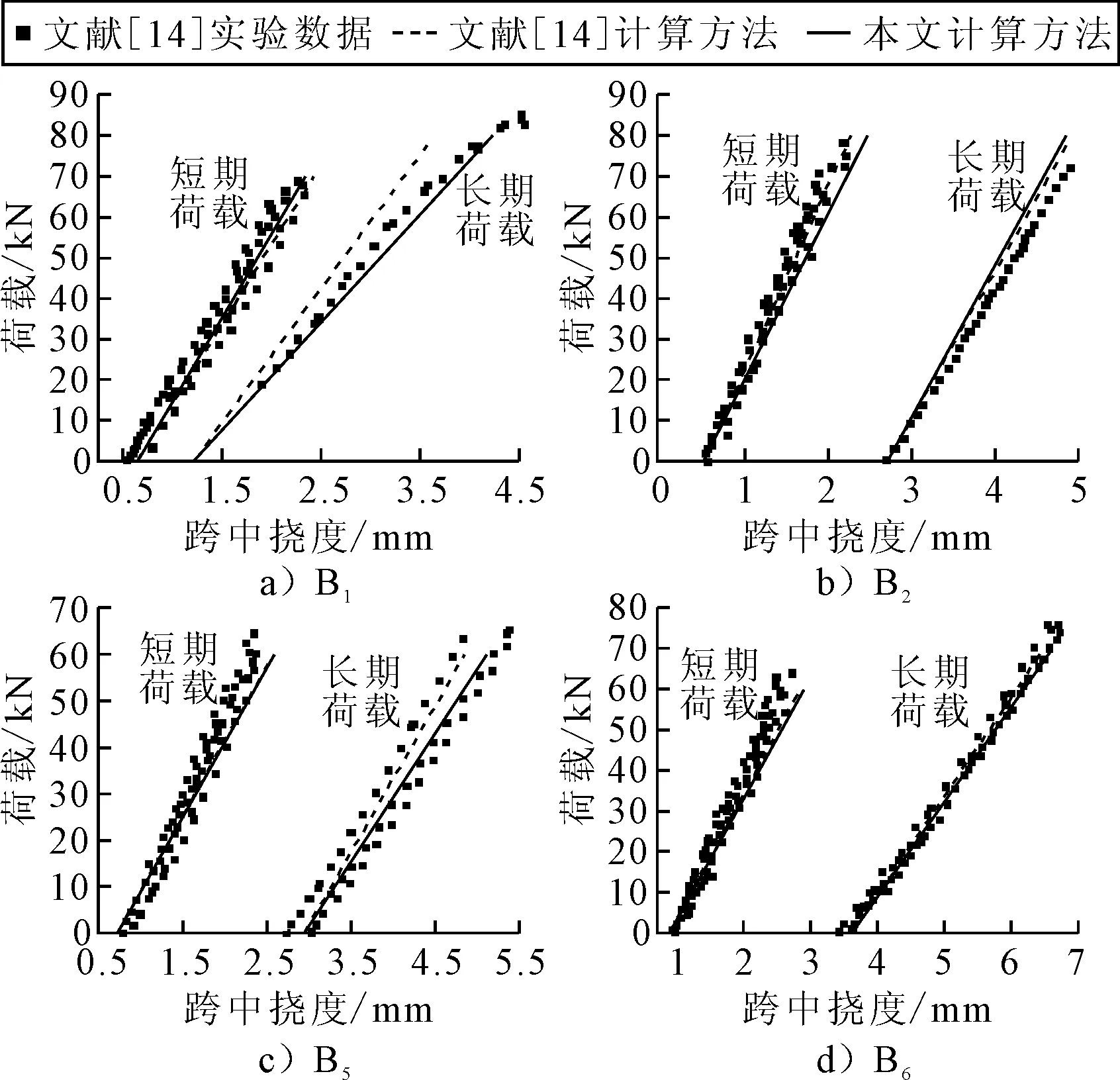
在荷载P0的作用之下,根据内外力平衡,在两个荷载之间所有的截面的内力主矩都等于M0=P0×lp.圣维南原理揭示了若把物体的一部分边界上的面力变换为分布不同但静力等效的面力,近处的应变分量将有显著的改变,但截面横断面尺寸之外所受的影响可以不计.因此,可以认为裂缝的影响区域lef等于截面的高度h,在裂缝左右侧1倍梁高范围以内(即lc-lef 1.1.1黏结区域 这个区域距离裂缝最远,因此其黏结性能最好,认为钢筋应变εt与周围混凝土应变εcl相等. εt=εcl (1) 然后裂缝会削弱梁底部的混凝土应变,由于此区域距离裂缝最远,所以该区域内梁底部混凝土应变变化缓慢,假设在这个区域内,梁底部的混凝土应变从εcb0均匀变化到0.95εcb0.其中:εcb0为距离裂缝h处的混凝土底端应变,可用经典梁理论求得. (2) 式中:I0为完好梁的惯性矩;Ec为混凝土弹性模量;yn为y方向中性轴距离梁底部的距离. 黏结区域的长度lb与钢筋对混凝土开裂的限制作用有关,通过钢筋形心到裂缝上方混凝土的形心hp来计算.约束作用越大,裂缝带来的削弱效应越弱,混凝土应变变化越慢,变化所需的子区域越长.所以lb随着hp的增大而增大,假设lb与hp的函数关系式为 lb=lef(0.1+0.7ρ2) (3) 式中:ρ为hp与h的比值,当ρ趋向于0的时候,钢筋对混凝土无约束作用,此时,钢筋混凝土梁可视为均质素混凝土梁,Chun等[5]指出:对于开裂均质素混凝土梁而言,底部应变从εcb0变化到0.95εcb0所对应的区间长度为0.1lef.当ρ趋向于1的时候,钢筋几乎位于梁体的外侧,此时钢筋的约束作用最强,黏结区域的长度也就最大,所以当ρ的取值范围为0到1,lb随ρ增大而增大. 1.1.2滑移区域 该区域相较于黏结区域更加接近裂缝,因此裂缝对该区域的影响要大于黏结区域,梁底部的混凝土应变进一步减小,相对应的钢筋的应变却增大,钢筋和周围混凝土开始出现滑移,因此钢筋应变不等于混凝土的应变εcl.Manfredi等[6]指出:在裂缝附近存在一个特殊截面,受压混凝土的应变与受拉钢筋的应变近似满足平截面假设,此截面钢筋应变为 (4) 式中:dt为钢筋形心到混凝土底板的距离;εct为混凝土顶板应变,假设这一特殊截面位于滑移区域,且与裂缝距离为0.2lef. 对于特殊截面附近的截面而言,可以根据钢筋与钢筋附近有效面积内的混凝土的内力平衡来计算,假设有效区深度为(dt+7.5db).其中:db为钢筋直径.有效区域内钢筋与混凝土的拉力之和保持不变,为 EtεtsAt+EcεcbsAce=EtεtjAt+EcεcbjAce (5) 式中:εcbs为特殊截面上有效区混凝土的应变;εtj和εcbj为待求截面上钢筋与混凝土的应变;Ace为有效区面积;Et为钢筋弹性模量,如果已知混凝土应变εcbs和εcbj,即可根据式(5)求解出εtj. 由于存在裂缝,且滑移区端部接近裂缝,故底部混凝土应变逐渐减小,并在滑移区域的末端应变趋近于0,可以认为:该分区内,从远离裂缝到接近裂缝时底板混凝土应变从0.95εcb0线性变化到0. 1.1.3剥离区域 该分区是最靠近裂缝的分区,钢筋与混凝土之间几乎没有连接,梁底部附近的混凝土的应变为0,但是钢筋存在很大的拉应力,并与混凝土应变无关. 由于混凝土与钢筋之间不存在黏结,故可以认为在此分区内钢筋的应变保持一致,钢筋周围混凝土应变为0,故可根据式(6)计算钢筋应变. (6) 由于钢筋与混凝土独立变形的区域较短,假设剥离区域长度为0.1lef.则滑动区域的长度为影响区长度lef减去剥离区域与黏结区域的长度之和. 在裂缝影响范围内混凝土应变沿梁高方向呈现非线性变化,明显不满足平截面假定.而且,截面离裂缝越近,非线性效应则越明显. 在黏结阶段,由于距离裂缝最远,受到裂缝的影响相对微弱,因而采用最简单的非线性应变分布模型——双线性应变分布模型,见图2a),在高度等于裂纹深度dc的位置出现拐点.因此,混凝土沿高度的应变分布为 (7) 式中:εcb为混凝土底板应变. 在滑移区域,截面更靠近裂缝,底部混凝土应变沿梁轴线减小.但裂纹尖端以上的应变增加,包括拐点处的应变.因此,拐点处的应变将大于底部的应变,非线性变得明显.假定拐点以下的应变服从非线性分布,见图2b).混凝土应变分布为 (8) 式中:参数α表示其非线性,这里假设为3. 在剥离区域,当尖端附近的应变集中时,尖端上方的应变分布也变得非线性.假定中性轴以上部分的混凝土应变与高度呈线性关系,而中性轴与裂纹尖端之间部分的应变与中性轴垂直距离的平方根成正比,见图2c). 图2 横截面正应变分布模型示意图 裂纹尖端以下的应变分布也假定为一条三次曲线,但该分布的高度随截面到裂缝的距离变化而变化.在滑移区域和剥离区域的结合部分,此分布的高度为(dc-dt).因为裂纹表面没有力,所以在裂缝截面处,此分布高度等于0.假设高度沿梁轴线性变化.因此,剥离区域的混凝土应变分布可以写成 (9) 式中:εcp为应变分布拐点混凝土的应变值;dz为位于裂纹尖端以下应变等于0的的高度. 虽然建立了不同的模型来描述钢筋混凝土的黏结损伤和非线性混凝土应变分布,但这些模型中仍存在一些未知数,如混凝土顶部应变εct和中性轴位置yn.为了解决这些未知问题,对受弯梁采用了以下截面内力平衡. (10) (11) 式中:Ac和At为混凝土和钢筋的面积 首先,在黏结区域中,底部的混凝土应变是根据1.1提到的钢筋混凝土黏结滑移模型获得的,钢应变εt可以根据式(1)和式(5)用混凝土应变表示. (12) 但是在式(11)中仍然有两个未知量,顶板应变εct和中性轴高度yn,将已知量代入力和弯矩平衡方程可以得出: (13) EtεtAt(dt-yn)=M0 (14) 式中:Acu和Acb为拐点上、下的面积. 在滑移区域,特殊截面的钢筋应变可以通过混凝土的应变来表示,首先根据力和弯矩平衡方程求解该截面内的未知数,对于其他截面,可在特殊截面确定后可通过式(5)来估算出其他截面的钢筋应变,从而用同样的方法求解未知数. 在剥离区域,钢筋应变保持一致,且可通过剥离区域与滑移区域交界面处的钢筋应变得知,而且已有的文献表明:靠近裂缝时,截面的中性轴高度几乎处于相同的高度,故认为从特殊截面到开裂截面的中性轴位置保持不变,但是剥离区域多出一个未知量εcp.通过联立方程组求解出未知量εcp和εct. 当相邻裂缝间距大于2lef,可以认为两个裂缝影响区域不互相影响,用上述方法挨个求解单个裂缝影响范围内的应变分布情况,即可知道整个梁体的钢筋混凝土应变分布情况. 当相邻裂缝间距小于2lef,两条裂缝同时影响截面的应变分布.为了考虑这种影响效应,首先假设截面仅受距离截面最近的裂缝的影响,建立了黏结损伤和应变分布模型;然后根据距离截面稍远的裂缝对截面的影响,对模型中的参数进行修正,最后通过内力平衡求解模型中的未知数. 由于裂缝的存在降低了底板应变,两条裂缝影响下的应变比仅一条裂缝影响下的应变小,可以认为εcbm比假设仅受最近的裂缝的影响求解出来的地板应变εcb1小. εcbm=βεcb1 (15) (16) 式中:εcb2为假设截面只受距离截面第二近的裂缝的影响求解出来的底板应变;β为修正参数,取值范围是(0,1]. 由于两个裂缝同时作用于模型,模型的非线性将增大,因此通过修改表示非线性的模型中的参数α对混凝土应变分布模型进行修正,将其改写为 α=int(3/β) (17) 式中:int(x)为对x进行四舍五入的取整运算. 对黏结损伤模型和应变分布模型进行修正以后.模型中的未知数仍然通过内力平衡来求解.求解后,可以得到截面的顶部应变和中性轴. 上述三种应变分布模型均具备同一特点,即中性轴至梁体顶部应力呈线性分布,三个关键截面处的曲率κ为 (18) 式中:εct为梁顶部混凝土的应变.各关键截面处弯矩均为M0,由经典梁理论,截面等效惯性矩计算表达式为 (19) 根据上述三种应变分布模型未知量的求解,可以知道整个简支梁任意截面的梁顶部混凝土的应变εct与梁中性轴高度yn,故而可以计算出简支梁所有截面的等效惯性矩. 使用梁有限单元法求解此开裂钢筋混凝土梁在静力荷载下的响应.将跨径为L的简支梁等分为ndiv个单元,共有(ndiv+1)个节点,每个节点具有两个自由度(竖向位移与转角).第i个单元的端节点编号为i与(i+1),其单元刚度矩阵Kme为 (20) 式中:E为单元的弹性模量,近似为Ec;ξ为单元局部坐标系内的局部坐标,等于(x-xi)/(xi+1-xi).其中:xi、xi+1为单元端点i与(i+1)的整体x坐标;If(ξ)为单元长度范围内以局部坐标表述的等效惯性矩表达式,可以通过Ia(x)得到;N(ξ)为梁单元的Hermite形函数. 将单元刚度Kme组合成总体刚度Kb,由节点内外力的平衡,代入简支梁边界条件,求解线性方程组,即可得出任意节点处的挠度和转角. 该组实验由François 等[7]完成,该简支梁长度为3 m,计算跨径L=2.80 m,梁高h=0.28 m,梁宽b=0.15 m,结构配筋图及裂缝分布图见图3,裂缝信息见表1.钢筋的屈服强度为500 MPa,弹性模量Es=200 GPa;混凝土的抗压强度为63 MPa,抗拉强度为6.8 MPa,弹性模量Ec=35.0 GPa. 图3 三点加载矩形简支梁结构布置及裂缝分布图(单位:mm) 表1 三点加载矩形简支梁裂缝信息表 m 采用第1节提出的方法能够求解整条梁裂缝影响范围内所有截面的等效惯性矩,未处于裂缝影响范围内的截面的惯性矩按完好梁惯性矩处理.全梁范围内等效惯性矩分布图见图4. 图4 三点加载矩形简支梁等效惯性矩分布图 在简支梁跨中加载集中力,得出跨中挠度同跨中弯矩之间的关系见图5.由图5可知,本文提出的方法的计算结果无论是相对于欧洲规范计算结果还是相对于文献[17]所提出的计算结果,都与实验数据更加接近,验证了提出的刚度计算方法的适用性.且本方法所需考虑的参数较少,仅需通过裂缝的位置和深度信息,即可得知全梁范围内等效惯性矩分布,易于编程计算. 图5 三点加载矩形简支梁跨中弯矩-位移关系图 Teng[8]以试验梁进行四点加载实验,得出荷载大小和跨中挠度的关系.梁全长为3.5 m,计算跨径为L=3.3 m,矩形截面高h=0.4 m,厚为b=0.3 m.钢筋的保护层c=0.035 m.测得混凝土的28 d平均抗压强度为46 MPa.钢筋直径为16 mm.钢筋的屈服强度为500 MPa.弹性模量Es=200 GPa;混凝土的抗压强度为63 MPa,抗拉强度为6.8 MPa,弹性模量Ec=33.8 GPa.钢筋布置图及荷载示意图见图6,选取其中的四片梁进行分析,他们的编号为B1,B2,B5,B6.裂缝分布图见图7. 图6 四点加载矩形梁钢筋布置及荷载示意图 图7 四点加载简支梁梁裂缝分布图 由于文献[8]中的裂缝是弯曲的,而且南北面裂缝分布不一致,不利于计算,故需要采用以下方法将弯曲的裂缝等效成在同一截面的裂缝: 在梁的正视图上用一系列间隔10 mm的水平线去划分裂缝,裂缝与水平线相交于若干个点,接着将裂缝与水平线相交的点(若裂缝尖端不与水平线相交,则在裂缝尖端处补充一个点)的横坐标平均得到所需要的裂缝的位置,裂缝深度取裂缝尖端的纵坐标.得到各梁的裂缝信息表,限于篇幅,略. 以B1梁为例,分别求解出梁体南北面在不同裂缝深度及位置下的等效惯性矩见图8.由于此梁南北两面的裂缝信息不一致,故根据上文介绍的方法得到南北两面惯性矩不一致,此时做简化处理认为:梁的整体等效惯性矩为南北两面惯性矩的平均值,将南北两面的惯性矩求平均值,得到最终整个梁短期荷载下沿全长的惯性矩分布情况见图9a)实线,根据同样的方法可以求出B1梁长期荷载作用下的等效惯性矩见图9a)虚线以及其他梁全梁在短期和长期荷载作用下的等效惯性矩见图9. 图8 B1梁短期荷载作用下南面等效惯性矩分布图 图9 各梁全梁等效惯性矩分布图 在距离两端支座1.1 m处各加一个大小相等的荷载,得到各梁体跨中挠度和荷载的关系见图10,计算得到的直线与实验数据点的均方根见表2,由图10和表2可知: 表2 四点加载矩形简支梁均方差汇总表 图10 四点加载矩形梁跨中弯矩—位移关系图 1) 对比B1梁短期荷载与长期荷载下的实验数据发现,由于裂缝在长期荷载作用下裂缝得到了扩展,使得裂缝深度发生了变化,削弱了梁的抗弯刚度,导致B1梁长期荷载作用下抗弯刚度小于B1梁短期荷载作用下的抗弯刚度. 2) 对比B1梁短期荷载与B5梁短期荷载的实验数据发现,裂缝数量也同样影响带裂缝梁的抗弯刚度,当裂缝数量较多的时候会更多的削弱梁的抗弯刚度, 3) 本文所提出的方法能够反映开裂梁刚度随裂缝分布的变化,能更方便快捷的模拟出全梁的等效惯性矩,且通过本文提出的计算方法计算出来的荷载挠度曲线与实验结果吻合良好,进一步验证了第1节提出的计算方法的准确性. 提出一种综合考虑裂缝分布的刚度计算方法.首先基于梁的数量信息和位置信息确定裂缝影响范围,然后基于裂缝的深度信息提出了裂缝附近梁截面非线性应变分布模型,根据内力平衡方程,求解出各应变分布模型中的未知量,继而得出全截面处的等效惯性矩,得到梁的总体刚度矩阵,求解得到梁在不同荷载下各节点的竖向位移与转角. 提出的应变分布模型考虑了裂缝的分布信息,能够反映出裂缝尖端的应力集中现象及裂缝截面混凝土应力放散等现象,从而精细地反映实际开裂构件中裂缝影响范围之内的正应变分布规律.同时,根据裂缝信息得出的全梁范围内的等效惯性矩分布能够反映全梁范围内各截面的等效惯性矩,而不限于宏观尺度梁单元的平均等效惯性矩. 以三点加载矩形简支梁和四点加载矩形简支梁的响应计算为算例,计算结果同实验数据吻合良好,验证了提出的刚度计算方法具备较好的适用性.本文采用的方法只需知道裂缝的分布信息即可快速计算出全梁的刚度,能够较为方便地求解实际工程中开裂钢筋混凝土梁在外荷载作用下的响应.1.1 黏结滑移模型
1.2 横截面正应变分布模型
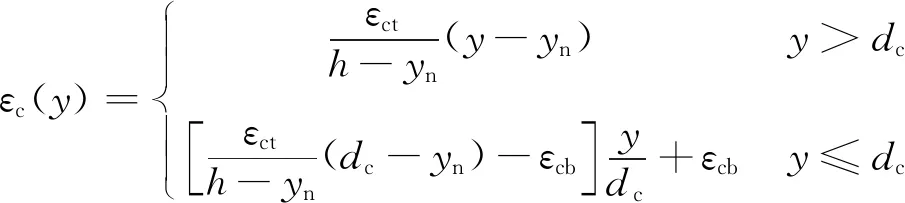
1.3 应变分布模型未知量的求解
1.4 相邻裂缝的应变分布
1.5 等效惯性矩求解
1.6 梁单元刚度矩阵的计算
2 算 例
2.1 三点加载简支梁



2.2 四点加载矩形简支梁
3 结 束 语
