室内二维弥散试验拖尾现象研究
2020-10-19顾家慧
陈 亮,张 赏,余 旺,顾家慧
(1.河海大学 岩土力学与堤坝工程教育部重点试验室,江苏 南京 210098;2.河海大学 岩土工程科学研究所,江苏 南京 210098)
随着社会的快速发展,人类的频繁活动,化肥和农药的大量使用,污水和垃圾的大量排放,尤其是核能源导致的核废料,不断往地下渗入,严重污染了土壤以及地下水[1-4]。在污染物防治的过程中,研究溶质运移的规律是其中关键。Fick基于弥散试验,将分子扩散定律应用在弥散问题中,但在实际情况中,溶质在多孔介质中的运移大多数是非费克的[5-9]。非费克现象主要包括非对称的拖尾或提前穿透等现象,其中拖尾现象一直是国内外学者们关注的焦点,即在已经遭受污染物污染的地区,往往很长一段时间内都会残存污染物,污染物长时间内无法消散,抑或是消散时间远超过基于Fick定律的理论时间。Neuman S P[10-11]等人认为溶质运移的拖尾现象是由土体非均质性导致的。Langevin C D[12]等人的试验结果表明,环境温度的变化和溶质的浓度变化也会导致拖尾分布,他们认为这些因素的变化会导致地下水密度的变化从而会对地下水的流速流态产生实质性的影响。王泽坤[13-14]等人研究发现了土体中含有的透镜体或者死端孔隙对拖尾现象也存在着不同程度的影响。徐玉璐[15]通过室内弥散试验,得到污染物浓度随时间以及距离变化的穿透曲线,每组试验中均出现拖尾现象,这种现象随着试样圆曲率的减小和粒径的增大而更加明显。由于传统对流-弥散方程描述污染物运移会出现拖尾现象,因此本文建立了指数衰减函数模型来描述C-t曲线下降段和拖尾现象,并通过室内二维弥散实验结果来验证模型拟合度,分析了模型各参数的意义,以及污染物浓度和水力梯度对相关参数的影响。
1 试验原理及计算模型
二维弥散试验的理论模型见式(1),其解析解式(2)[16]可用来描述溶质运移过程,溶质运移曲线应符合正态分布,但实际情况中,由于土体的非均质性等因素,溶质运移并不符合正态分布,解析解不能准确描述实验结果,尤其是浓度下降段与理论值相差比较大,即出现拖尾现象(图1)[17]。
(1)
(2)
图1(来自文献[17])表明通过模型的解析解对试验值进行数据拟合时,浓度下降段相差较大,溶质浓度降为本底值的时间比理论值慢了很多,说明在实际情况中,污染物在理论时间内并没有消散,仍有残留,经过较长一段时间才逐渐消散,试验值与解析解拟合值相差较大。基于传统对流-弥散方程描述污染物运移会出现拖尾现象问题,以及无法描述拖尾现象,本文尝试建立描述浓度下降段拖尾现象的理论模型。
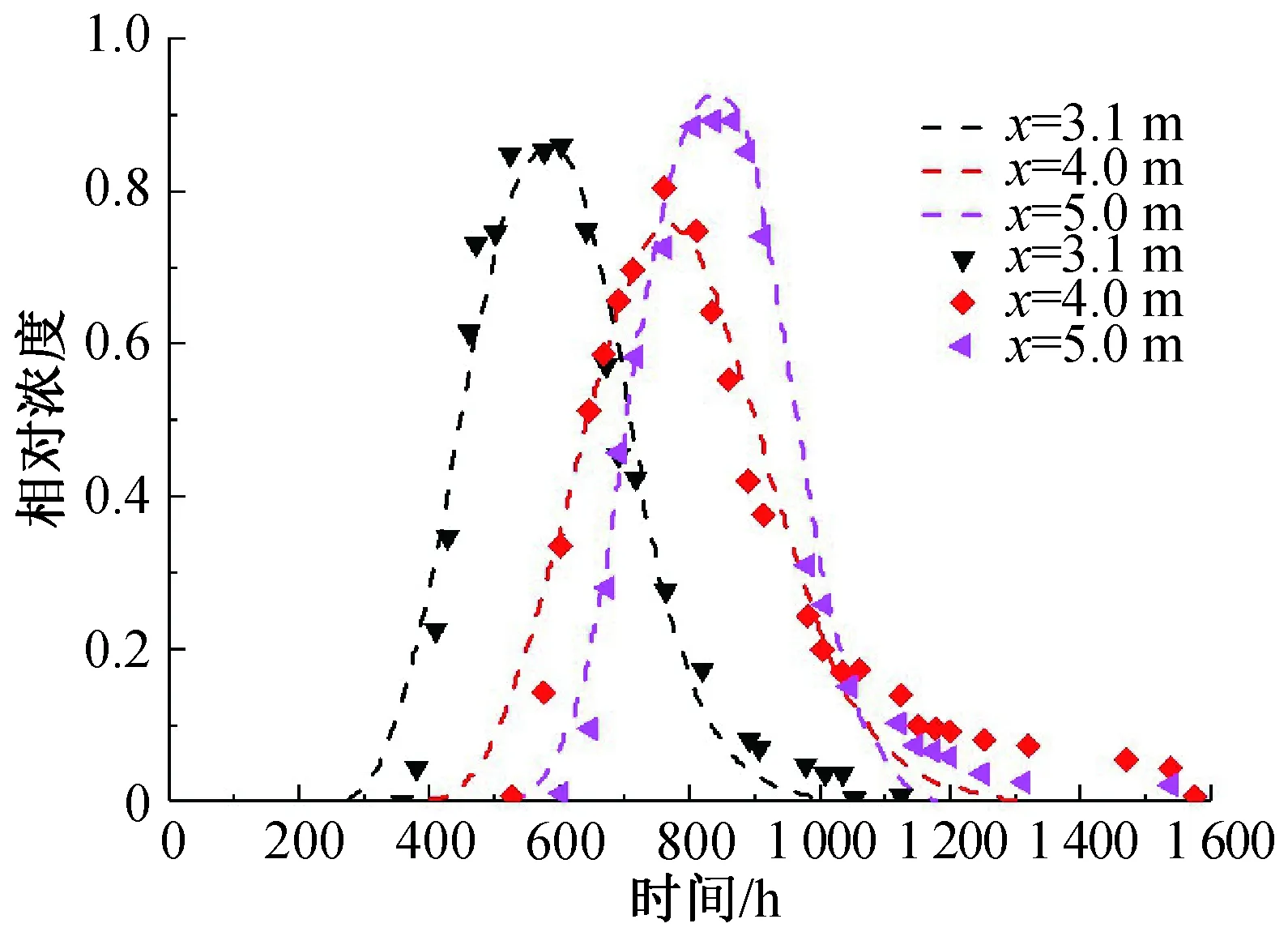
图1 溶质运移拖尾现象
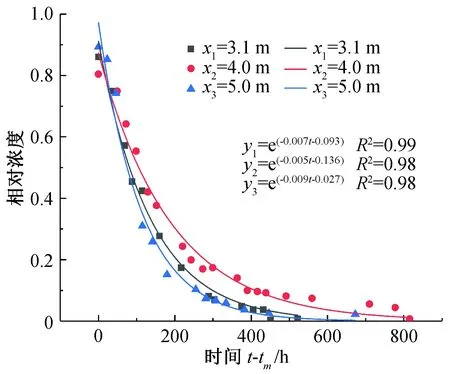
图2 文献17数据拟合结果
拖尾现象主要发生在浓度下降段,因此在讨论拖尾现象时,单独考虑C-t曲线的下降段。在峰值时间处将C-t曲线分开讨论,C-t曲线下降段从峰值时间tm开始,各组试验tm不同,为方便研究,统一去掉峰值时间,即t-tm。从图2可以看出,C-t曲线下降段从峰值时间开始,浓度随时间变化接近于指数衰减分布,因此认为C-t曲线下降段符合指数衰减规律,尝试基于指数衰减函数对C-t曲线下降段进行拟合。Moser[18]等人根据点稀释定理,建立了描述示踪剂在某一点处稀释的模型:
Ct=C0e-Bt
(3)
其中:C0为初始浓度;t为时间;B系数与流量以及滤水管半径有关。氯化钠溶液浓度与电导率呈线性相关,即C0/Ct=N0/Nt,代入式(3)中得:
Nt=N0e-Bt
(4)
该模型描述了某一点在t0时刻,浓度从初始浓度C0开始,随着时间不断变化的过程,这一过程和二维弥散试验中C-t曲线下降段较为相似,基于该模型,对式(4)进行修改,建立相关指数衰减模型,用以描述C-t曲线下降段。
Nt=N0e-α(t-tm)-β
(5)
其中:Nt为某时刻的电导率,N0为投源孔初始浓度,α,β为参数,t为时间,tm为峰值时间。采用图1(文献[17])中的数据对公式(5)进行拟合,结果如图2所示,R2均在0.98以上,说明拟合效果较好。
为研究式(5)中参数α,β的含义,对式(5)两边同时取对数,得式(6):
(6)
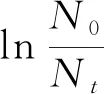
2 试验部分
2.1 实验装置
为了验证上述指数衰减模型的可行性,讨论模型中参数α,β的含义及影响因素,找出污染物浓度、水力梯度以及距离对拖尾现象的影响规律。为此开展常水头下室内二维弥散试验,试验装置如图3所示,该装置能够较好地模拟不同水力梯度和不同污染物浓度下污染物的运移情况。自制透明有机玻璃长方形试验槽,模型的上游为进水室,下游为出水室,填土槽尺寸为900 mm×400 mm×90 mm,填土槽位于两块过滤板之间,过滤板的作用是缓冲水流,保证弥散试验过程中流场始终为二维稳定流场。将PVC管进行钻孔打眼,作为室内弥散试验所用的观测井,并在外围用两层80目滤网进行包裹和绑扎,防止砂土进入测井内造成堵塞,又能保证水和溶质顺利通过测井。弥散试验中各个测孔的分布图如图4所示,试验前,按方案设置好各个观测孔,并进行编号,从投源孔开始为0—9#。在二维弥散试验中,投源孔的作用是投放示踪剂,距离上游进水室1 500 mm,观测孔分为主测孔和旁测孔,每个观测孔直径均为32 mm。

图3 试验模型装置图
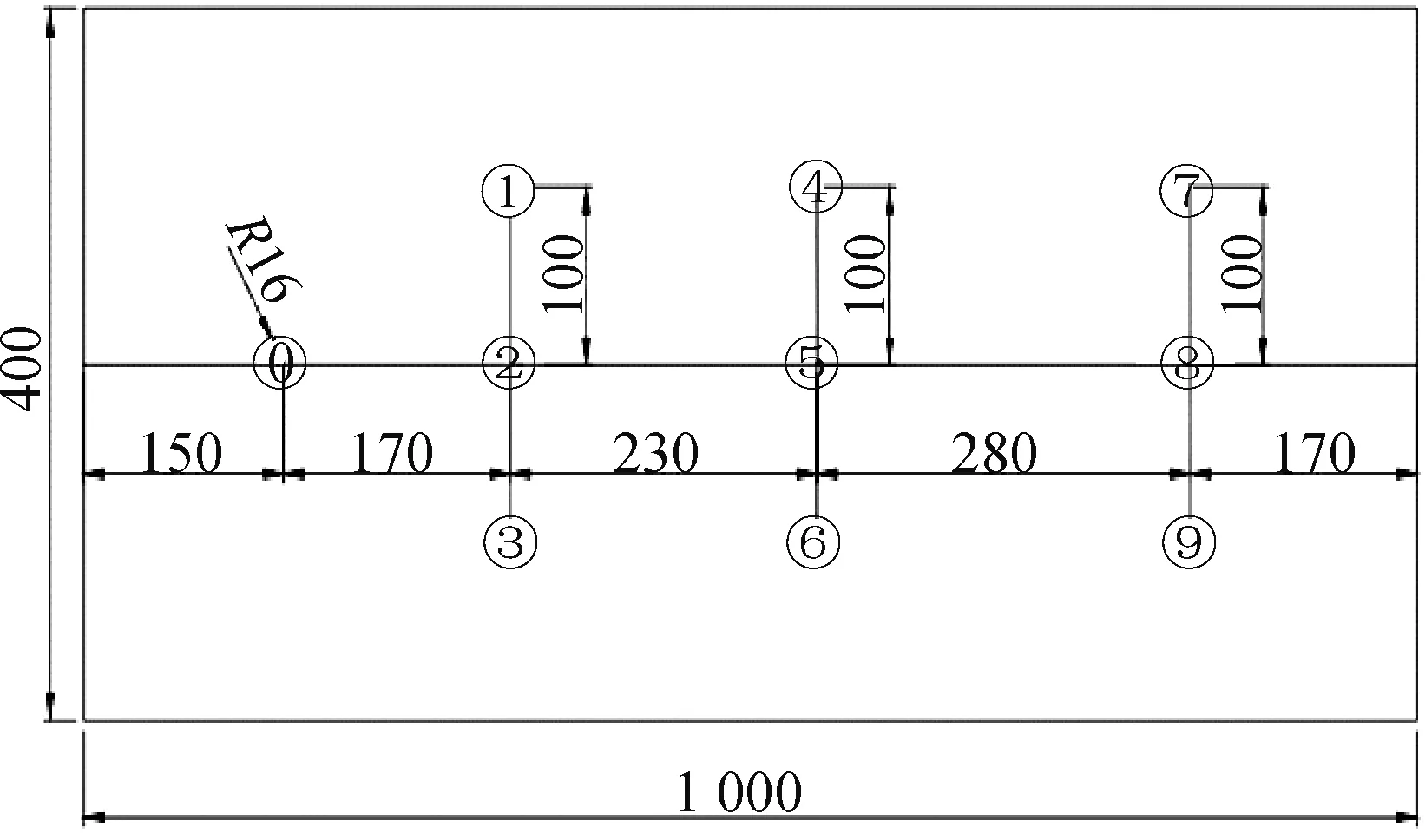
图4 测孔分布图(单位:mm)
2.2 试验材料和试验方案
由于土体非均质性对弥散试验拖尾现象影响程度较大,为研究拖尾现象随其他弥散因素变化的规律,本文选取均匀中砂作为试验土样,排除土体非均质性的影响。试验土样取自长江淡水沙,筛选粒径d≤2 mm的砂样,为保证土样中不存在其他杂质干扰试验结果,填样前使用清水洗涤。试验砂样的级配曲线如图5所示,从级配曲线看出,粒径大于0.25 mm的颗粒超过全重的50%,根据《建筑地基基础设计规范》的砂土分类,该土样为中砂。其不均匀系数Cu=d60/d10=0.35/0.18=1.94<5,颗粒均匀,为均匀中砂。用此砂样为试验土样,土样孔隙均匀,可看作为均质土体。
本试验采用NaCl作为示踪剂,通过电导率仪实时监测各监测孔中的电导率,然后通过电导率与NaCl 浓度的关系转换成 NaCl 的浓度,然后通过后续计算求解。图6为NaCl 溶液电导率与浓度关系图,由图可知两者为正比关系,因此可以用电导率仪来监测土体中的电导率,来代表土体中污染物浓度的大小。
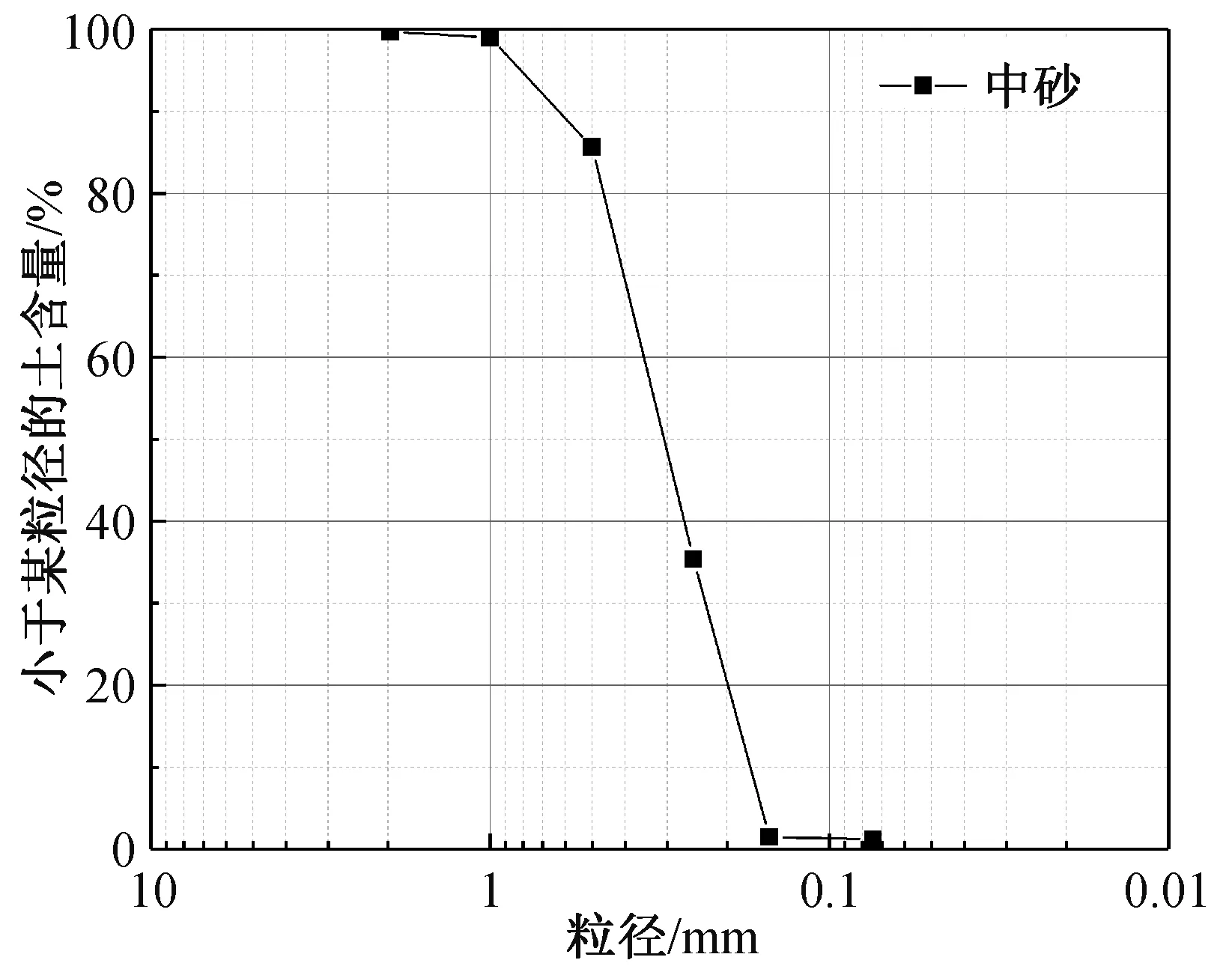
图5 试样级配曲线
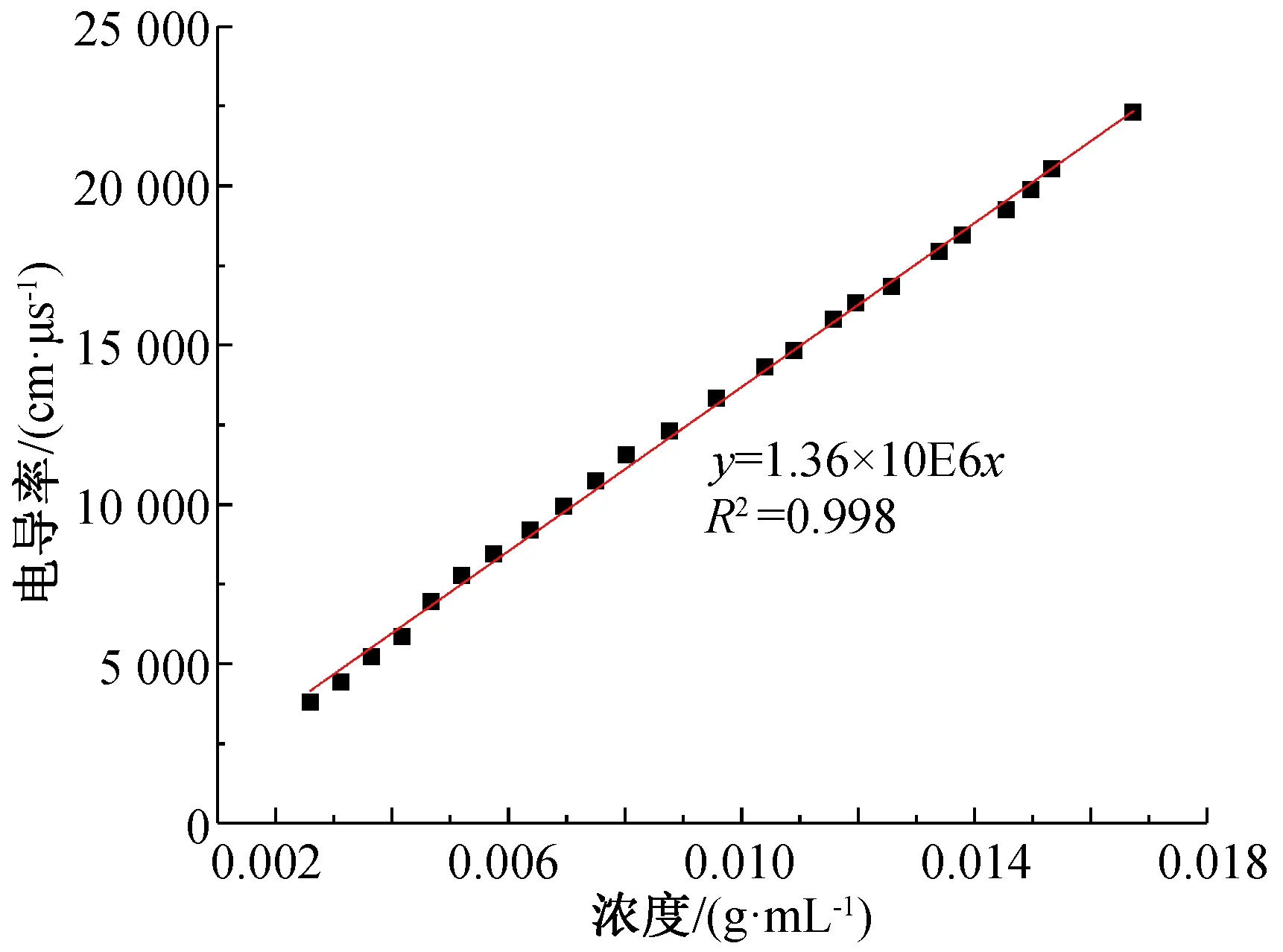
图6 NaCl溶液电导率与浓度关系
为研究污染物浓度和水力梯度以及距离和拖尾现象之间的关系,本文设计4组不同污染物浓度以及4组不同水力梯度下的试验方案,通过调节水箱高度改变水力梯度(试验模型所在高度为下游高度,水箱高度为上游高度),通过投放不同浓度的盐溶液改变污染物浓度。为方便表示,污染物浓度按以下公式计算:投盐质量(g)/溶液总质量(g),四组污染物浓度分别为5%、10%、15%、20%。具体试验方案如表1所示。
2.3 试验步骤
本次室内二维弥散试验过程主要分为以下几个步骤:装样、稳定流场,投放示踪剂,实时监测等。
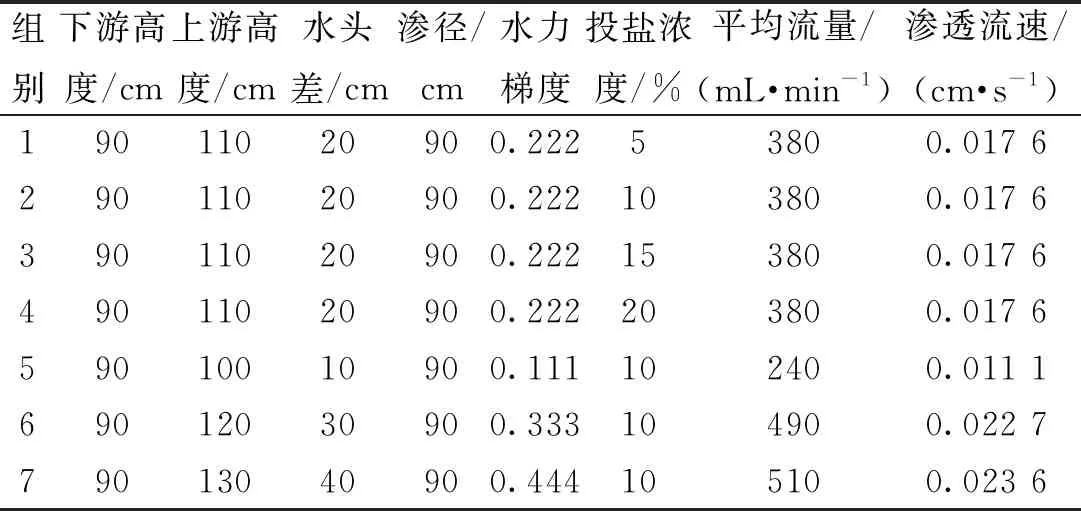
表1 试验方案
2.3.1 装样
装样前在模型槽四周涂上凡士林,防止土体两侧的流速过大,保证流场的稳定。分层装样,将试验晒干土样按照试验方案设定的孔隙比(本次试验孔隙比设为0.7)分三层进行装样。装样完成后,在土样上方覆盖一层1 mm厚的粘土层,防止土体上方流速过大,对实验结果造成影响。装样完成后,缓慢提高与上游进水室连接的水头,当水头高度略高于土样高度时,稳定水头,使土样处于饱和状态,为稳定土样中的流场,完全排除土样中的气泡,将土样持续饱和48 h。
2.3.2 投放示踪剂
选取瞬时投放作为本次试验污染物的投放方式。提前制备好NaCl溶液,选用长条塑料袋,宽度为6 cm,长度为80 cm,将制备好的NaCl溶液倒入塑料袋中,将塑料袋缓慢放入投源孔底部静置,待1 h后,待土样中的流场稳定之后,使用刀片将塑料袋割破,将塑料袋中的NaCl溶液流出,待塑料袋中的NaCl溶液全部流出后,缓慢拿出塑料袋,保证流场的稳定,随后进行各观测孔的检测。
2.3.3 检测
在投源孔投放示踪剂后,通过电导率仪按照测孔编号顺序对每个测孔进行电导率检测,对于每个测孔,相隔大致5 min读取一次数据,当每个测孔的数据都从初始值到达峰值再降为初始值之后,结束试验,之后开始下一组试验。
3 试验结果及分析
在本次二维弥散试验中,各组试验下均存在程度不一的拖尾现象,电导率下降段时间远大于上升段,如之前所述,应用二维对流-弥散方程难以描述电导率下降段,无法准确描述电导率到达本底值的时间,严重影响到污染地区的修复。为此本文将各组试验电导率下降段单独进行研究,在穿透曲线峰值和峰值时间处,将穿透曲线分为电导率上升段和电导率下降段,通过上述指数衰减模型对二维弥散试验浓度下降段进行拟合,发现各组试验拟合效果均较好,由于篇幅所限,部分拟合结果如图7所示,图7显示了在不同水力梯度和不同浓度下1#测孔试验指数衰减拟合结果,由图可知各条模拟曲线的相关系数均大于0.95,拟合程度较高,模拟效果较好,因此指数衰减模型可以较好地模拟污染物在各个测孔中从峰值浓度逐渐衰减的过程以及浓度下降段的拖尾现象。
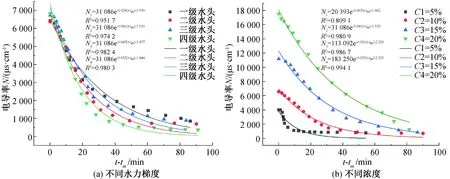
图7 不同水力梯度和不同浓度1#测孔试验指数衰减拟合
通过指数衰减模型对试验数据进行拟合,得到了不同试验条件下的α,β,为了研究α,β与试验因素间的关系,对α,β的定义进行验证,并进行相关分析,把α,β值进行整理(表2、表3)。
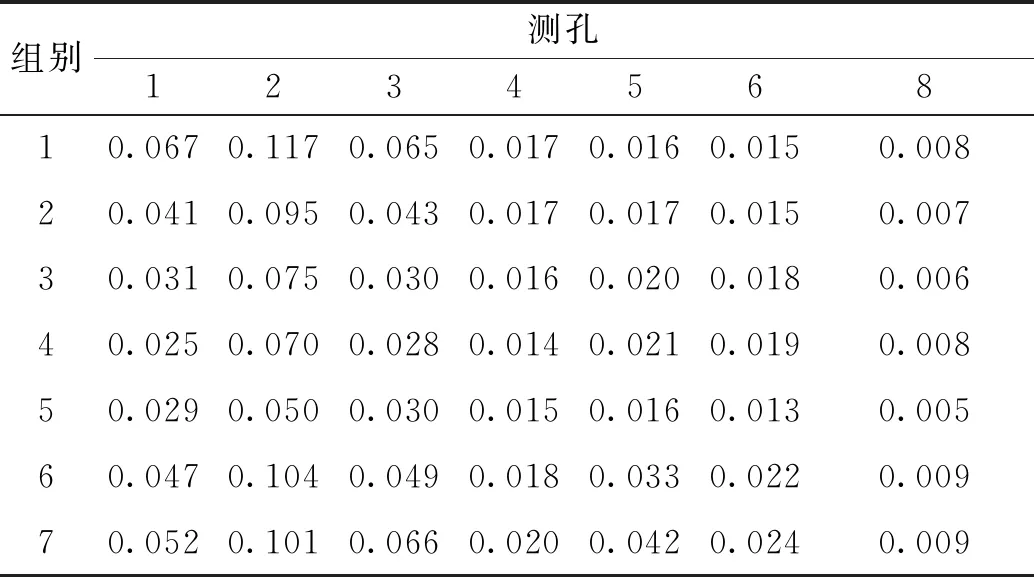
表2 各组试验下α值
3.1 污染物浓度与α,β关系
溶质运移主要基于对流作用以及分子扩散作用和机械弥散作用,分子扩散作用主要与污染物浓度有关,而污染物浓度是溶质运移的关键因素之一,图8为不同浓度下指数衰减方程拟合得到的α值,图8(a)(b)为同一横截面三个观测孔的α值,排除距离因素的影响。由图8可知各测孔的α值随着浓度变化发生较大的变化,随着污染物浓度的上升,各个测孔对应的α值均呈下降趋势,说明在相同的水力梯度下,污染物浓度越大,污染物的衰减速率越慢,拖尾时间也就越长,另外,图中显示2#和5#两个主测孔的α值均比其同一截面的旁测孔大,说明旁测孔的污染物衰减速率比主测孔小,意味着在同一横截面处旁测孔的拖尾时间比主测孔的拖尾时间大,即旁测孔的拖尾效应比主测孔的拖尾效应严重。
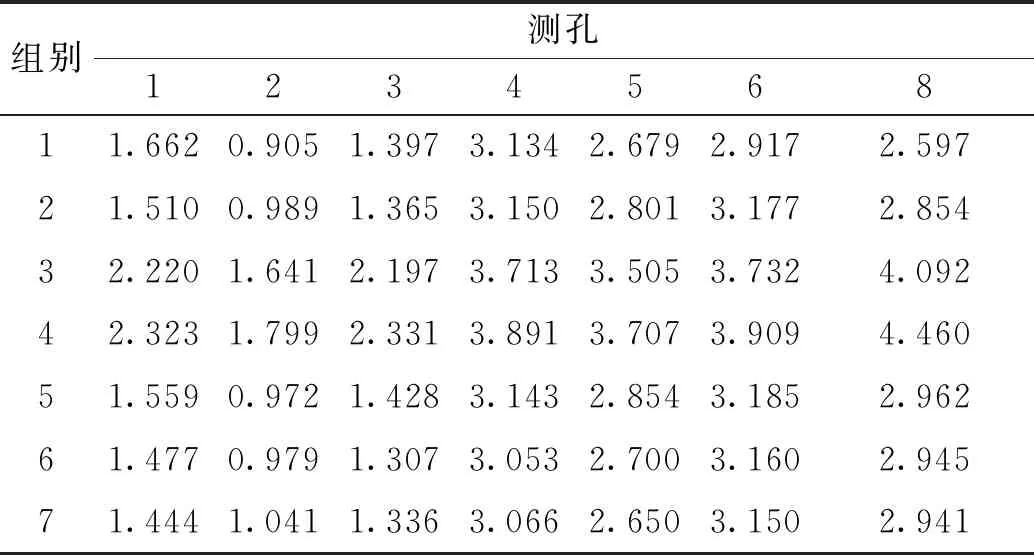
表3 各组试验下β值
图9为不同浓度下指数衰减方程拟合得到的β值,同样排除距离的影响,当浓度发生变化时,对应的β值也发生较大的变化。由于污染物浓度不同,初始投盐孔电导率有很大不同,其相应峰值电导率也不同,但从图9可知,在同一横截面上,β值随浓度的增加而增大,即投源孔初始浓度与测孔峰值浓度的比值随浓度的增加而增大。且在同一浓度下,主测孔的β值要比同一截面的旁测孔的值小,说明在同一浓度下,主测孔的C-t曲线的峰值浓度要大于相应旁测孔的峰值浓度。
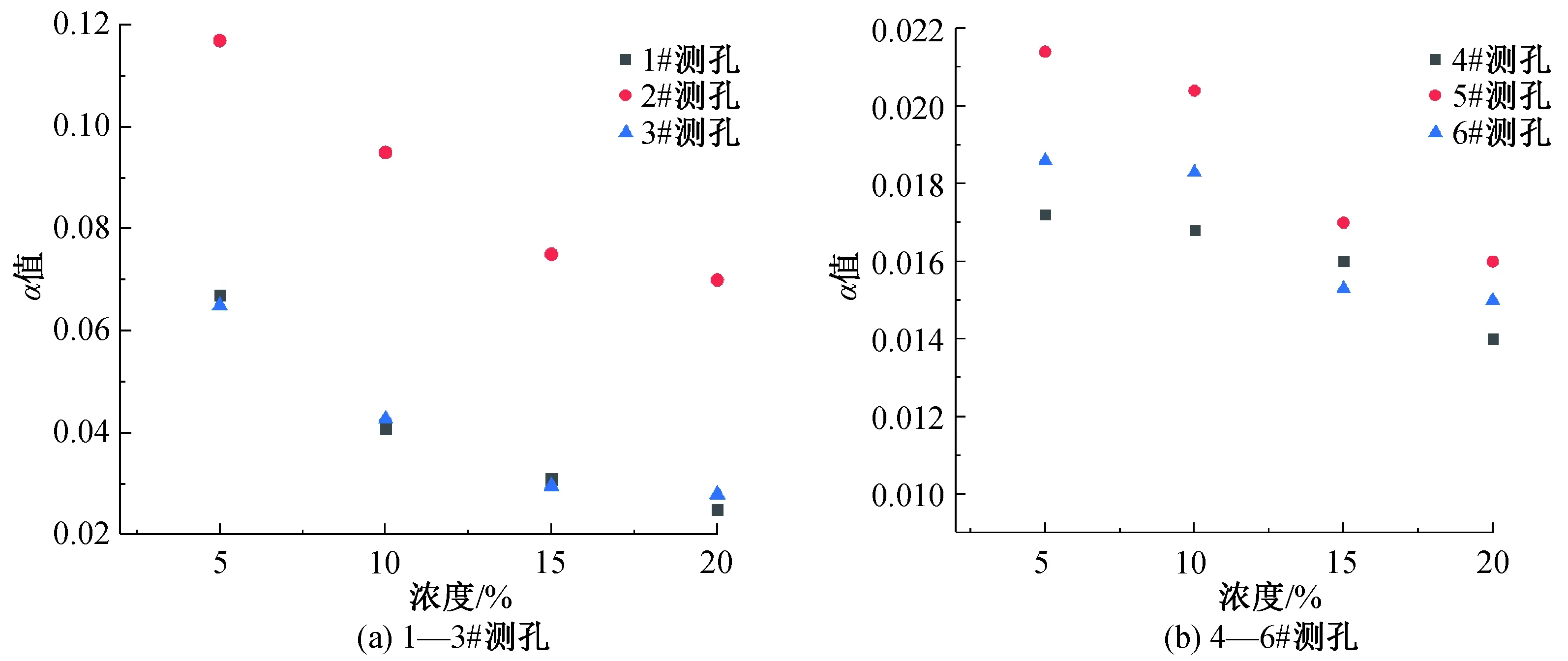
图8 不同浓度下的α值
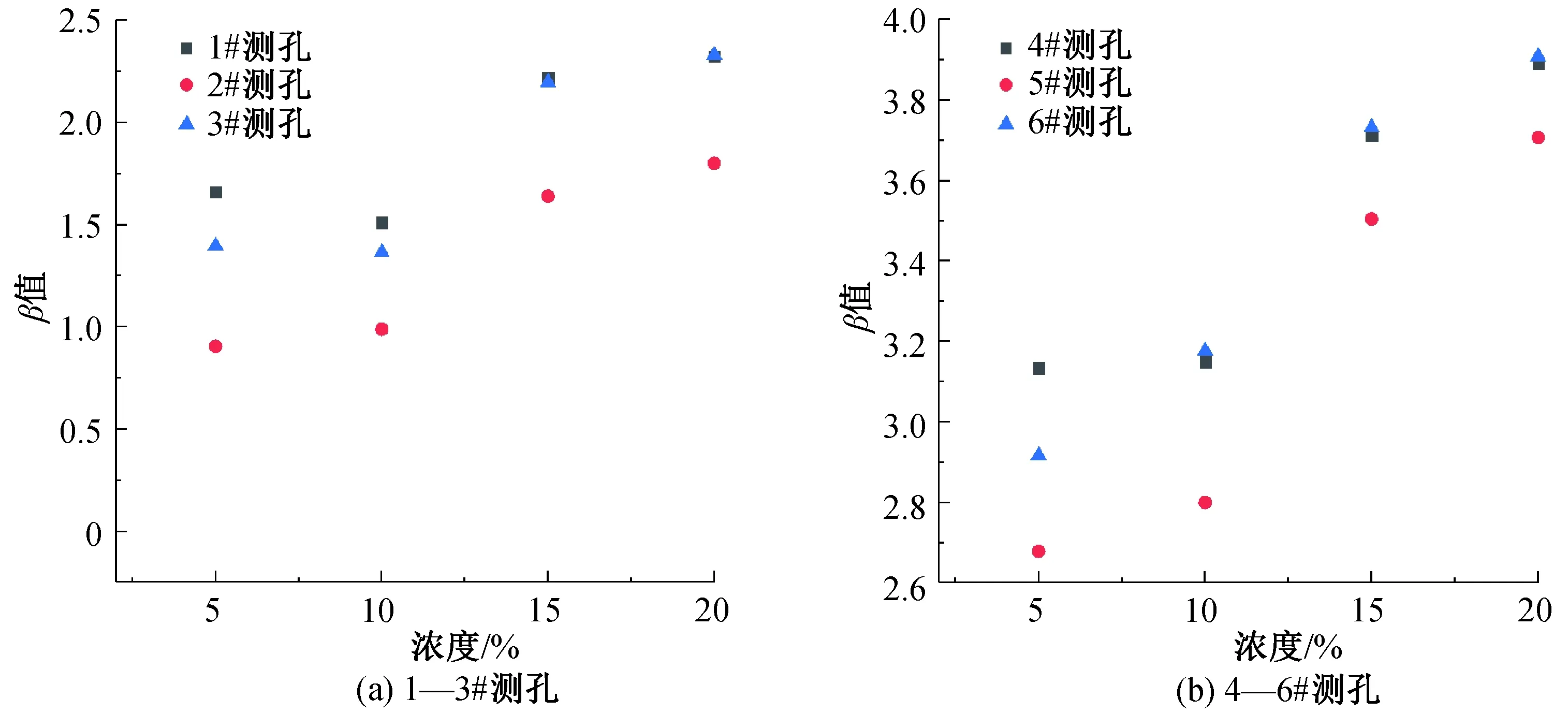
图9 不同浓度下的β值
3.2 流速与α,β关系
机械弥散作用是溶质运移的关键因素之一,为了研究α,β值是否与机械弥散存在联系,即α,β值是否与流速有关,通过指数衰减模型对不同水力梯度下的四组弥散试验拟合,得到不同流速下的α,β值,讨论α,β值与流速间的关系。图10为不同水头高度下的指数衰减方程拟合得到的α值,流速与水头高度成正相关,可以通过讨论水头高度与α值的关系得到流速与α值的关系。对同一横截面的三个观测孔进行研究,排除距离因素的影响。由图10可知各个测孔的α值均随着水头高度的增加而增大,说明随着流速越大,C-t曲线下降段衰减速度越快,拖尾时间越短,同时两个主测孔的α值比其两侧旁测孔的α值大,说明不论何种水头高度,主测孔的C-t曲线下降段衰减速率要大于旁测孔的衰减速率,即主测孔的拖尾时间小于其两侧旁测孔的拖尾时间。
图11为不同水头高度下的指数衰减方程拟合得到的β值。由图可知,当水头高度发生变化时,各测孔的β值变化幅度较小,说明不同水头高度对β值基本没影响,即流速的变化不会改变各测孔的峰值浓度,β值与流速无关。同时,两个主测孔的β值均小于同一横截面旁测孔的β值,说明在同一水头高度下,主测孔C-t曲线的峰值浓度要大于相应两侧旁测孔的峰值浓度。
3.3 距离与α,β关系
图12为不同距离的3个主测孔由指数衰减方程拟合得到的α值,从而排除流向的影响。不论何种水头高度和浓度,α值均随着距离的增加而降低,说明随着距离的增加,即离投源孔越远,C-t曲线下降段衰减速度越慢,拖尾时间越长,拖尾现象越严重。
图13为不同距离的3个主测孔由指数衰减方程拟合得到的β值,从而排除流向的影响。由图13可知不论何种水头高度和浓度,β值均随着距离的增加而增大,说明随着距离的增加,即距离投源孔越远,C-t曲线浓度峰值就越小,即污染物从投源孔运动到远处是浓度峰值逐渐递减的过程。
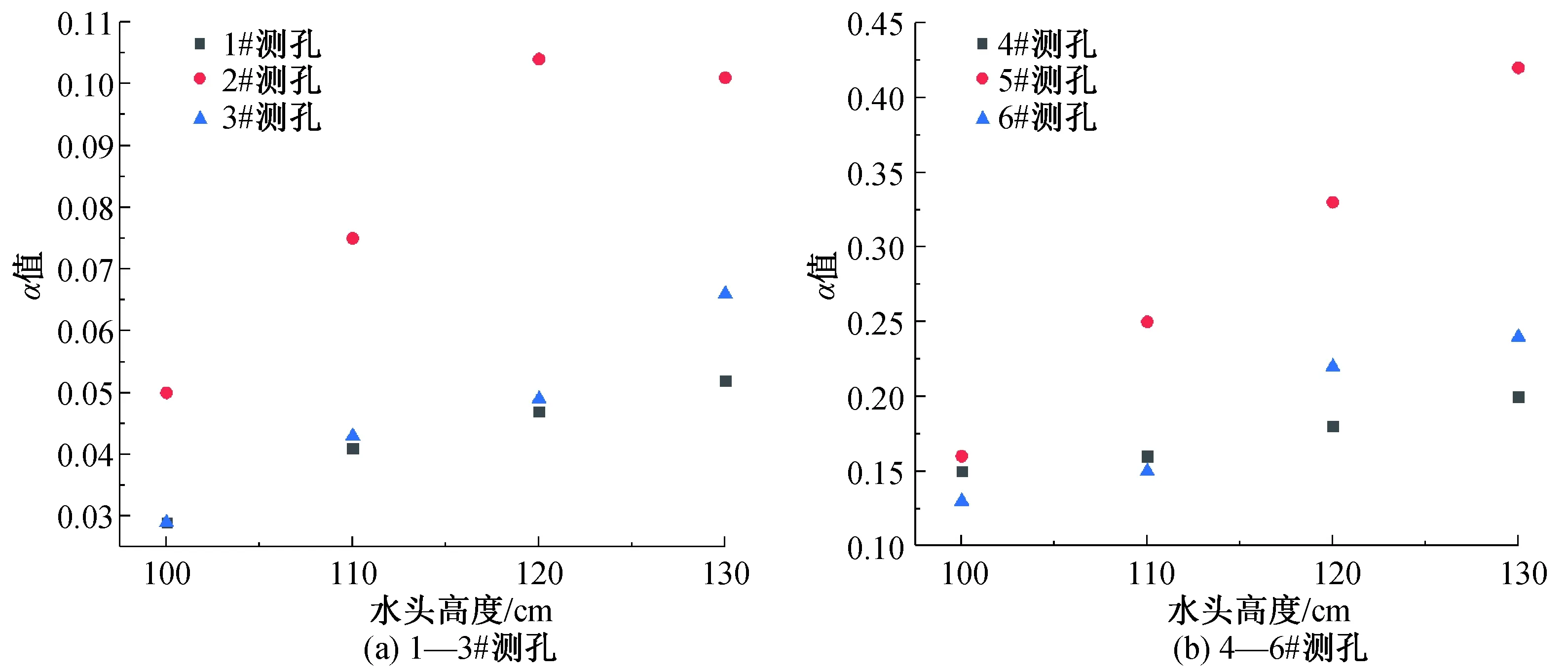
图10 不同水头高度下的α值
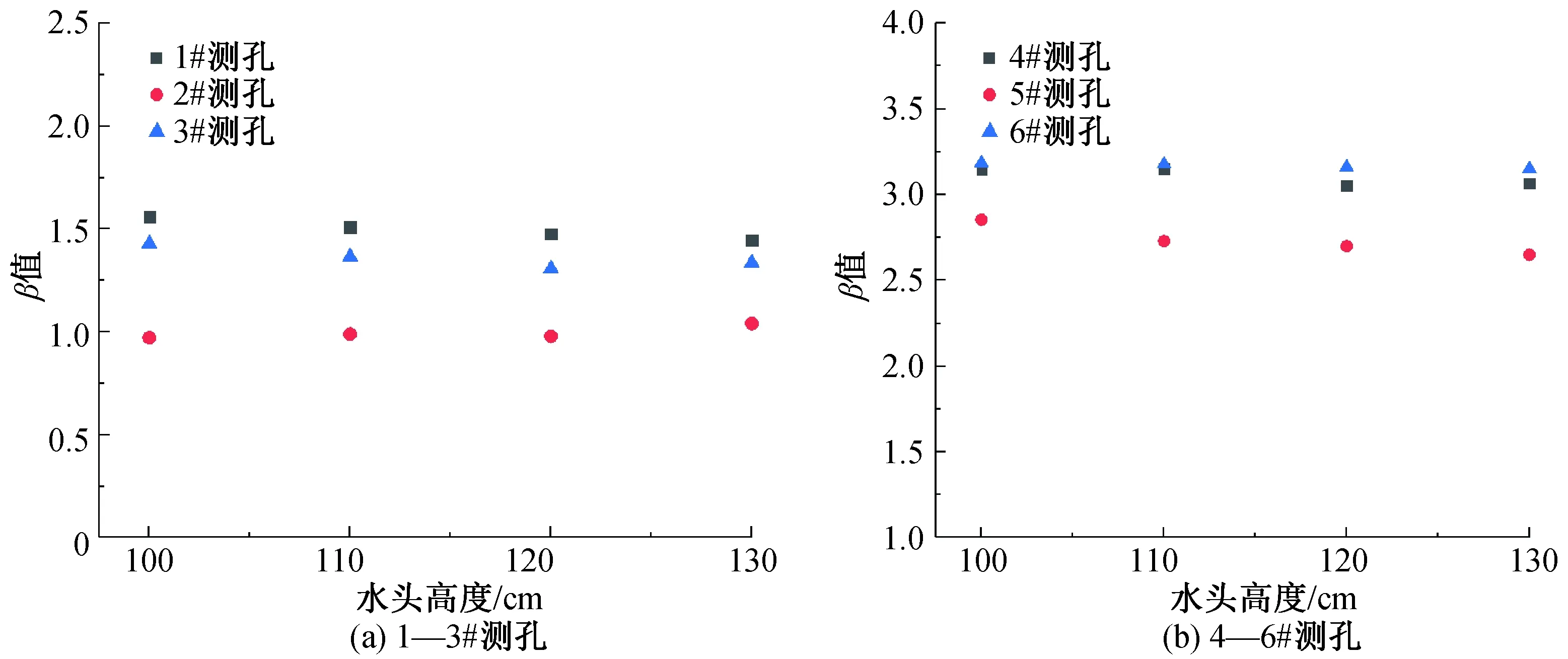
图11 不同水头高度下的β值
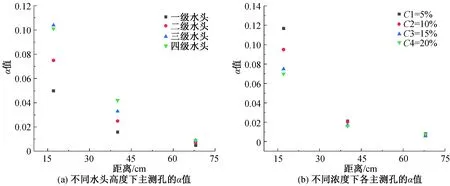
图12 不同距离下的α值
4 结论
1)各组试验均存在严重的拖尾现象,污染物浓度降为本底值的时间远大于理论值。
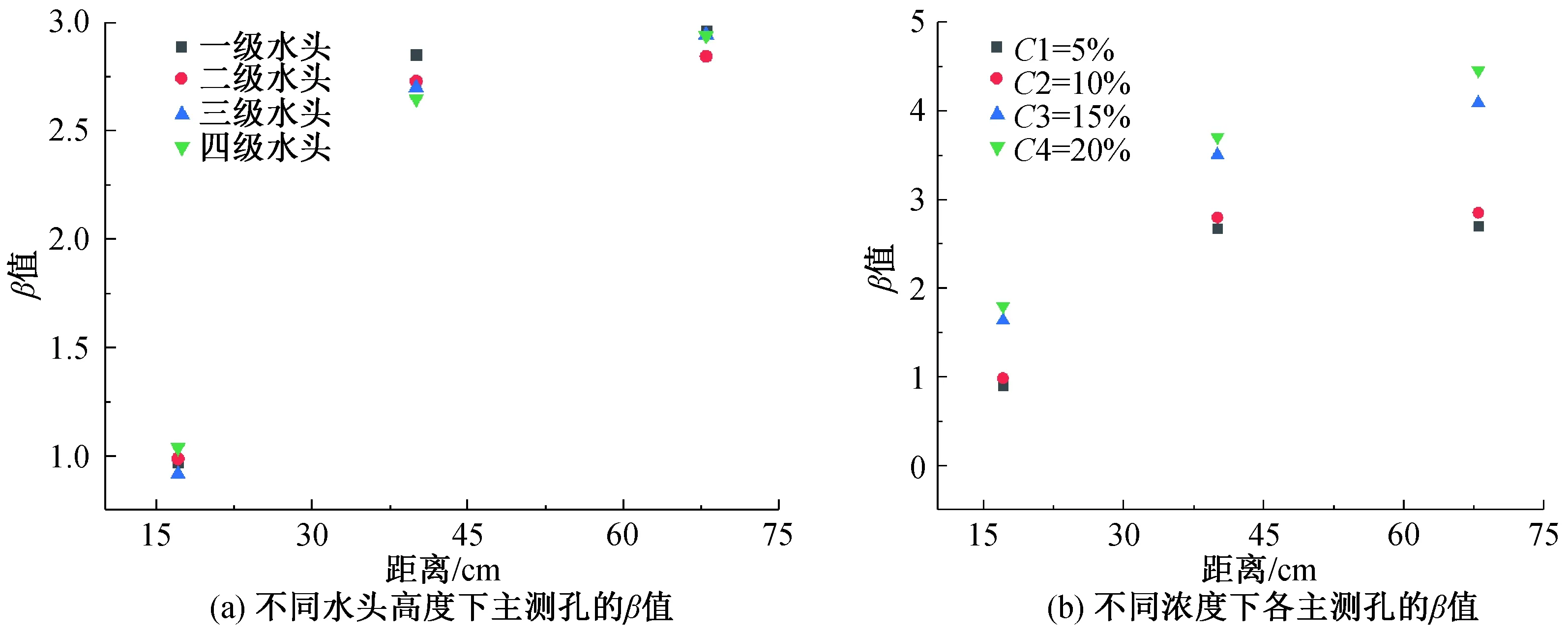
图13 不同距离下的β值
此将试验穿透曲线分为上升段和下降段,通过建立指数衰减模型对C-t曲线下降段拟合,拟合程度很高,说明污染物从浓度峰值降为本底值的过程为指数衰减过程,指数衰减模型能更好地描述C-t曲线浓度下降段的拖尾现象。
2)指数衰减模型中α是与污染物运移过程中弥散作用有关的参数,表示C-t曲线下降段的浓度衰减速率,α越大,浓度衰减速率越快,拖尾时间越短。β为和污染物浓度有关的参数,表示投源孔初始浓度与其他测孔峰值浓度的比值,β越小,C-t曲线的浓度峰值越大。
3)污染物浓度越大,则α值越小,衰减速率越慢,拖尾时间越长,同时β值越大,投源孔初始浓度与测孔峰值浓度的比值越大;水力梯度越大时,流速越大,则α值越大,拖尾时间越小,而β值基本不变,与流速无关;距离投源孔的位置越远,α值越小,衰减速率越慢,拖尾时间越大,β值也越小,即C-t曲线浓度峰值越小。
