基于R2指标的高维多目标差分进化推荐式课程系统
2020-10-18郝秦霞
郝秦霞
(西安科技大学通信与信息工程学院,西安 710054)
(*通信作者电子邮箱haoqinxia@126.com)
0 引言
“六卓越一拔尖”计划2.0 的正式启动标志着中国高等教育改革发展逐步走向成熟[1],中国高校积极探索“互联网+教育”“智能+教育+新形态”[2],构建多目标灵活的高等教育体系和评价体系[3],实现人才培养从同质化向多样化。
在智能教育新形态[4]的背景下通过分析历史行为数据,预测、推荐式的网络教学平台成为“互联网+教育”模式[5]主流,而教学推荐系统算法主要是基于内容的推荐和基于协同过滤的推荐,如姚敦红等[6]介绍了三维有偏权值张量分解在授课推荐上的应用,何杰光等[7]介绍了一种矩形邻域结构的教学优化教研模式,Hou等[8]介绍了基于动态自适应教与学优化算法的WebGIS 课程教学评价,管皓等[9]介绍了动态数学数字资源开放平台的设计与实现。各种推荐式的创新教学模式在不同程度上存在以下问题:
1)网络教学平台提供的网络课程教学覆盖的范围庞大,缺乏学科统筹设计,多形态的教研方式中学生对课程的选择没有合理的推荐方式,课程难以构成体系。
2)微课、慕课、混合教学等远程协同教学是以单数据为驱动的教研方式,是对教研活动中组织形式与技术手段的融合研究,未针对学生个体的特征、意愿建立适合面向学生的知识学习渠道。
3)未以“学生-老师-课程-评价”多元关系建立多目标效果评估,多目标数据未能体现出全局最优解,学生难以根据自身实际情况精准引导式地进行课程选择。
4)目标优化的方法在有限计算资源条件下,虽解集能获得较好的收敛性和分布性,但在实际工程领域中难以满足多目标优化问题求解需求,求解精准度需进一步提高,最终实现精准课程推荐。
为了解决以上问题,本文以学科分类为背景,提出基于R2 指标的高维多目标差分进化算法R2-MODE(R2 based Multi-Objective Differential Evolution),提高算法在高维复杂空间中的搜索能力;对各类多目标数据给出明确定义,并提出对课程教师推荐、专业相关度、课程难度系数、课程综合评价这4 项控制指标进行优化,建立高维多目标优化模型。最后利用课程属性数据集进行课程引导推荐实验,与主流推荐算法进行对比来验证本文方法在课程引导推荐上的准确性。
本文的主要工作:
1)在“互联网+”的大背景下,针对网络教学平台研究了引导式课程推荐在多目标数据时选课决策问题,实现精准的课程搜索方案。
2)给出多目标数据中各种指标数据的明确定义,进行了函数优化,分析建立了目标关系之间的相关性。
3)设计基于R2-MODE多目标数据模型,将切比雪夫函数作为R2指标排序的效用函数,提高了选课决策结果的收敛性和多样性。
1 问题描述
多目标推荐式选课系统程需要充分实现对于系统内学习资源的有效分配以及学生学习积极性的调度,合理地按照学生的学习计划实现课程推荐是研究的关键。一个合理的科学的课程推荐机制应该考虑到学生自身的学习喜好、学科类型、课程授课教师信息、课程信息、课程评价、课程相关度等多目标数据,这些多目标数据包括结构化、半结构化和非结构化数据。最终要筛选出匹配学生能力以及计划的课程,以满足不同阶段学生的个性化学习需求。
对比国际QM(Quality Matters)标准和国内FD-QM 标准(FD-QM 高等教育在线课程质量标准),结合中国高等教育实际情况,以最大限度减少数据存储量为目标,本文定义了课程推荐中的4 种类型目标数据。针对多目标数据在多维数据视图下构建数据仓库,最终实现高维多目标差分优化模型。
1.1 问题定义
本系统采用多维数据视图的数据仓库,构建用于课程推荐的多维数据模型,存储教师信息、课程信息、学生评价、课程维度、课程相关度系数等的多维空间数量值。为了把较小的维表联合在一起来改善查询性能,系统采用雪花模型的选课教学信息仓库,结构如图1 所示。图1 中Course ID 表示课程编号,课程集合course={c1,c2,…,cn};Student ID 表示学生编号,学生集合student={s1,s2,…,sn};Teacher ID 表示教师编号,教师集合teacher={t1,t2,…,tn}。在多目标教学系统中,所选定的参数指标为“学生正在选修的课程”“学生已经完成的课程”“系统内已发布的课程”,对于Course ID 设置标志位,“学生正在选修的课程”设为flag1,“学生已经完成的课程”设为flag2。由此将学生的这两项描述参数构成一个学生需求向量,用此需求向量对课程集合进行遍历操作,操作去除学生已经完成课程的记录,即学生正在选修以及选修完成的课程越多,课程推荐也就越详细,对学生推荐的课程更符合其之前的学习计划,很好地解决学生在完成或正在学习一门课程时,下一步学习课程推荐计划问题,是一种较为高效并且可行的推荐机制。
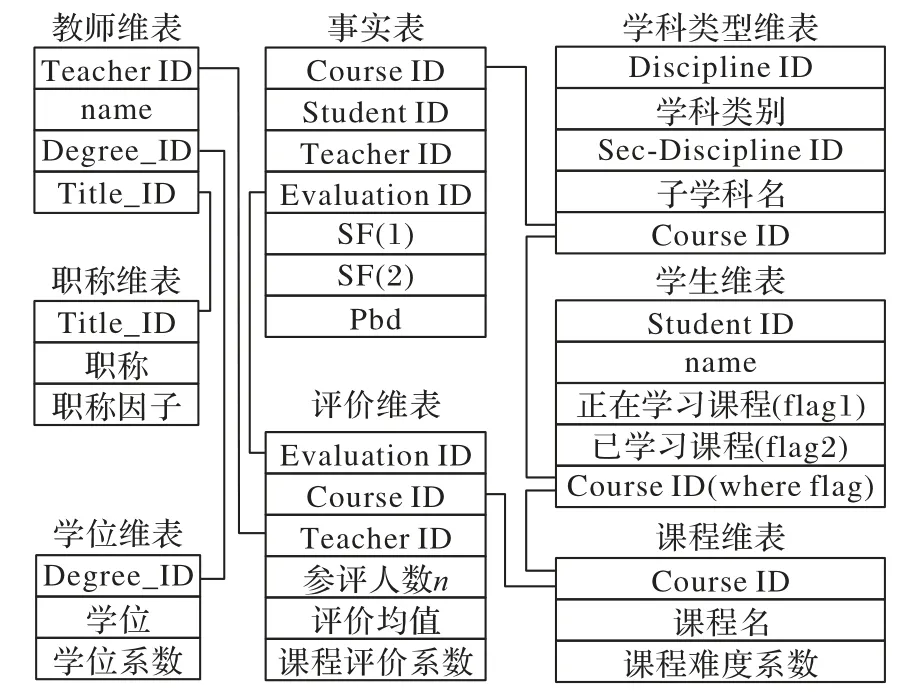
图1 雪花事实数据仓库模型Fig.1 Fact data warehouse of snowflake model
对于课程、学生、教师、课程难度、课程推荐指数等数据仓库中的相关属性进行形式化定义以及规约处理:
定义1教学名师因子(Teacher factor,Tf)。用来规约课程授课教师的职称,院士及以上Tf=0.5,教授Tf=0.4,副教授Tf=0.3,讲师Tf=0.2,助教及其他Tf=0.1。
定义2学位因子(Degree factor,Df)。用来规约课程授课教师的学位,博士Df=0.5,硕士Df=0.4,学士Df=0.3,其他Df=0.2。
定义3课程教师专业度(Teacher relationship,Tr)。用来规约课程主讲教师的专业性,值越大表示主讲教师的专业认可性越大。
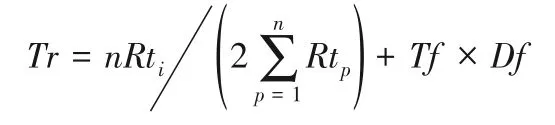
其中:n表示授课教师取得的学位数;Rti表示授课教师的第i个专业与所授课程的相关性。Rti取值范围定义如下:
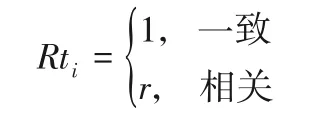
其中:r(0 <r<1)表示相关性系数。
定义4专业相关度(Professional relationship,Pr),0.1≤Pr≤1。用来规约课程的专业相关度。定义给定课程为C,子学科合集为H,一级学科合集为U。存 在,C∈Hi∈Uq|C∈Hj∈Uq|C∈Up因而Rdi(i=1,2,…,l)表示课程与一级学科的相关度,Rsi(i=1,2,…,k)表示课程与子学科的相关度。Pr值越大表示课程相关度越大。
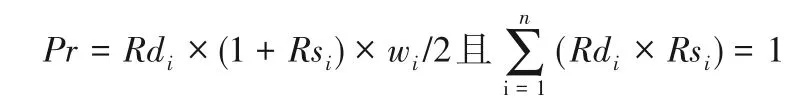
其中:n表示课程的总数;Hi、Hj为任意一级学科包含的任意子学科;Uq、Up为任意一级学科。wi为课程专业权重值,定义如下:

定义5课程难度系数(Course difficulty coefficient,Cd),0.1≤Cd≤1。用于规约课程难度的指标,指标越大表示课程的学习难度越高。课程的难度系数取值来自于系统专家教师、完成课程学习的学生网络投票问卷。问卷内容包含对其他先导课程的评定,最终给出个人难度评定。给定每门课程的难度系数区间[Cmin,Cmax],参与学习的学生越多,结合的个人实际情况对课程的投票结果越公正。Cd取值区间[0.1,1],难度系数Cd为:
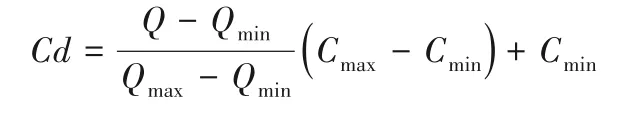
其中:Q表示课程的难度值,系统专家教师和学生对课程给出难度值的权重比例为w∶(1-w);p为系统专家教师的问卷量;q为完成课程学习的学生问卷量;Adi为问卷给出的难度值。
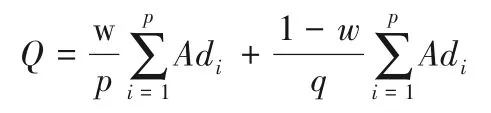
定义6课程综合评价(Course evaluation,Ce)(0.1≤Ce≤1):表示课程的综合评分,分值越高表明课程越实用,越被学生接受。Ce取值区间[0.1,1],C′max为课程综合评价最大值,C′min为最小值。课程综合评价Ce的计算公式为:
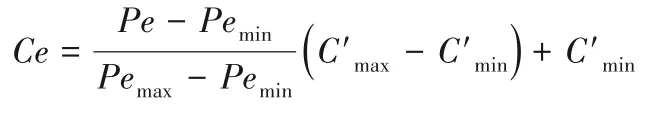
课程随着时代发展而不断地修正,因而设Pe为课程参与评价的年均分。Tyn表示在第n(1≤n≤N)年参与评价的专家教师数,Ten(0≤Ten≤100)表示此课程在第n年给出的评价值。Syn表示在第n年参与评价的专家教师数,Sen(0≤Sen≤100)表示此课程在第n年给出的评价值,系统专家教师和学生对课程综合评价的权重比例为v∶(1-v)。在第N年课程Pe表示为:
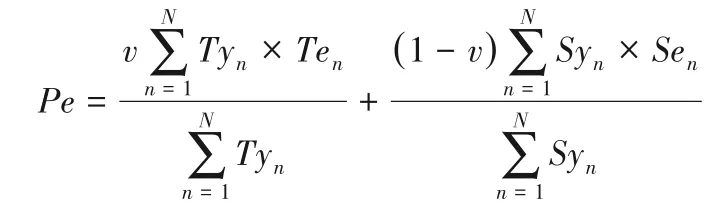
1.2 多目标课程引导教学模型
多目标推荐选课系统包含的课程教师推荐、专业相关度、课程难度系数、课程综合评价4 项推荐评价指标,从不同角度反映了课程的质量。而最佳课程质量的推荐应体现出4 项指标在一个学生发出学习诉求时达到全局最优策略,完成高维目标优化。通过平行空间内搜索最佳的推荐组合方案,实现4项指标的最优化。
在m维多目标优化模型中,考虑多目标优化需要统一目标最优化取值的极值性,其中Cd′(0 ≤Cd′)为选课者设定的课程难度系数,4个目标上的适应度函数值为:
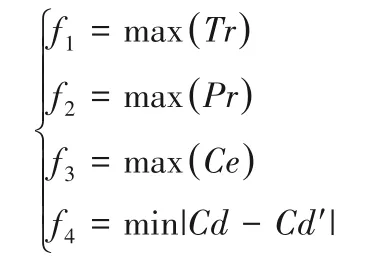
2 优化模型及算法设计
应用R2-MODE 求解选课推荐系统的4 目标优化决策问题的整体流程如图2所示。
为实现多目标推荐选课系统的4 项指标的最优化,应满足高维多目标优化问题,本文在目前主流的多目标优化算法(Multi-Objective Evolutionary Algorithms,MOEA)的基础上,提出R2-MODE 算法,增加目标选择的收敛性和多样性,并利用加权切比雪夫函数[10]作为R2指标[11]排序函数,作为选择标准来进行个体选择。
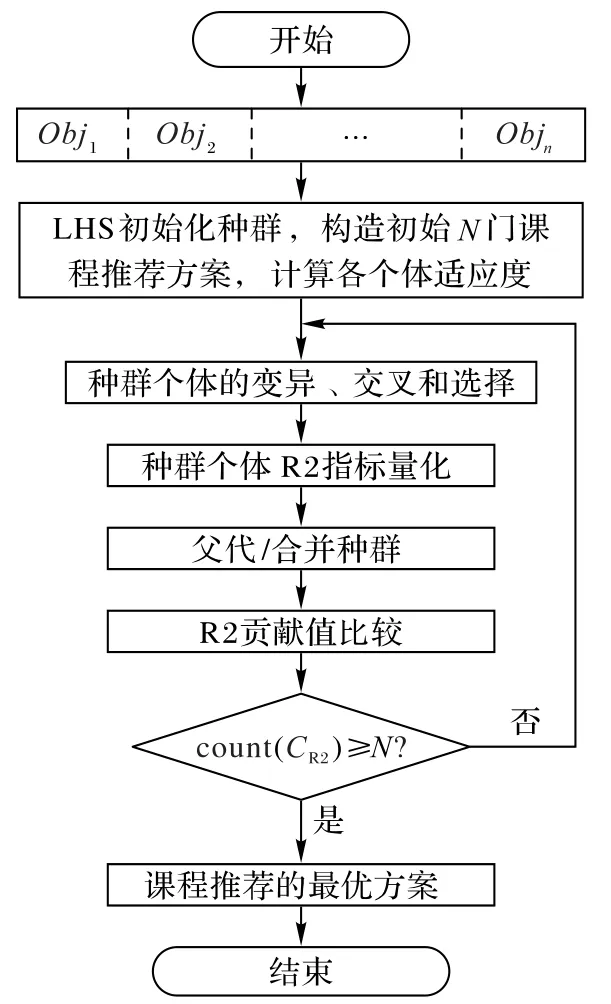
图2 四目标优化决策流程Fig.2 Process of 4-objective optimization decision making
2.1 基于R2指标的MODE的高维多目标进化算法
算法1 中R2-MODE 选用非支配解[12]指导种群进化,首先在目标解中生成N个均匀分布参考权重向量W,接着利用拉丁方抽样(Latin Hypercube Sampling,LHS)[13]随机均匀地分层抽样特性,保证初始种群的均匀分布采样。在主循环中,根据进化算法MODE[14]对父代种群Pt进行变异、交叉操作产生子代种群Qt,再根据R2 指标从合并种群中进行环境选择,利用个体a∈A的R2 的贡献值进行R2 排序,根据排序结果从合并种群中选择N个个体Xi进入下一代,多次迭代后产生的非支配解集作为种群最优个体集合的最终信号控制方案。
算法1 R2-MODE算法框架。

2.2 种群的分解
算法2 中首先采用MODE 算法对父代种群进行变异、交叉产生Vt→Ut→Pt,获得非支配解集合At,并对种群中的个体Xj在第m个目标上进行目标值标准化,m∈[1,M]。fm(Xi)为目标个体在第m维目标上的归一化函数值。gm,max、gm,minx分别为当前种群Pt中所有个体在第m维目标函数上的最大值和最小值。
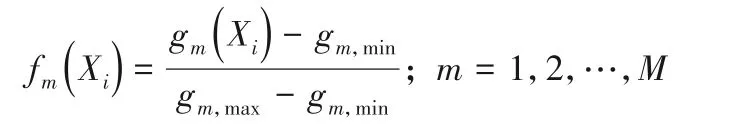
在算法2 的步骤4 中采用R2 指标定性评价两个近似PF的优劣,加权切比雪夫函数作为获得R2 指标排序的效用函数,将多目标函数整合成单一目标函数,以便优化不同类型的Pareto 前沿[15]。利用目标值作为该效用函数的一组候选解集A,αj为MODE 算法为在目标个体在第m维目标上的归一化函数值;一组权值向量Λ(λ=(λ1,λ2,…,λk)∈Λ)和理想点r*。
R2指标:
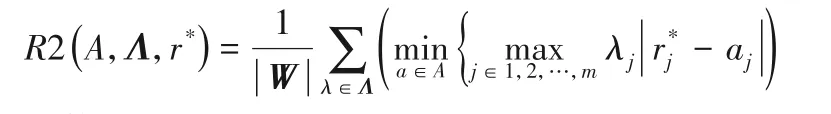
个体α∈A的R2的贡献值:
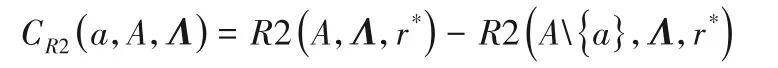
算法2 种群的分解。

2.3 算法复杂度分析
本文算法的计算成本来自于推荐式选课系统自定义模型和高阶差分算法中的个体选择。时间复杂度计算包括非支配排序和R2 指标贡献值计算,M为目标维数数,N为种群规模。非支配排序时间复杂度为O(N(1ogN)M-2),R2 指标贡献值计算时间杂度为O(MN2),且O(MN2)>O(N(1ogN)M-2),因而R2-MODE 时间复杂度为O(MN2)。与基于参考点的NSGA-III(Third version of Non-dominated Sorting Genetic Algorithm)[16]、基于支配关系的ɛ-MOEA(ɛ-dominance based MOEA)[17]以及基于排列的AR+DMO(Average Ranking method+Diversity Management Operator)[18]算法时间复杂度进行比较,NSGA-III时间复杂度计算包括个体进行非支配排序O(N2(1ogN)M-2)和基于参照点环境选择O(MN2),最坏时间复杂度为max{O(MN2),O(N2logN)M-2)},NSGA-III 时间复杂度为O(MN2)。ɛ-MOEA时间复杂度计算包括种群的规模与归档集维修,归档集规模设为k,时间复杂度为O(MN(N+K))。AR+DMO 时间复杂度计算包括AR 排序、DMO 对种群收敛性评价和分布性保持机制,且都为O(MN2),因而AR+DMO 时间复杂度为O(MN2)。
R2-MODE 算法没有增加算法复杂度,与NSGA-III、AR+DMO基本相同,优于ɛ-MOEA。
3 实验与结果分析
3.1 算法实验分析
为了评估R2-MODE 算法在多目标问题综合求解时的性能,与NSGA-III、ɛ-MOEA 以及AR+DMO 的结果进行实验对比。实验采用DTLZ 系列测试集,性能度量选取目前国内外主流的标准:世代距离(Generational Distance,GD)、分级度量(Diversity Metric,DM)和反转世代距离(Inverted Generational Distance,IGD),从收敛性、分布性和综合性作为评价标准。
3.1.1 测试函数
由于DTLZ[1~7]是用于评价高维MOEA 性能最广泛的测试集之一,目标个数可以任意设置,并且具有线性、凸凹面、多峰性、退化性,以及连续非连续性等特征[19],因而实验采用DTLZ[1~7]进行算法对比和性能分析。在测试集中,一个给定的M目标测试中,每一个目标函数的决策变量为n=m+r-1。测试问题划分为4、5、8、10 目标时,即:m∈{4,5,8,10},对于DTLZ1 设r=5,DTLZ[2~6]设r=10,DTLZ7 设r=20。DTLZ[1~7]的属性如表1所示。
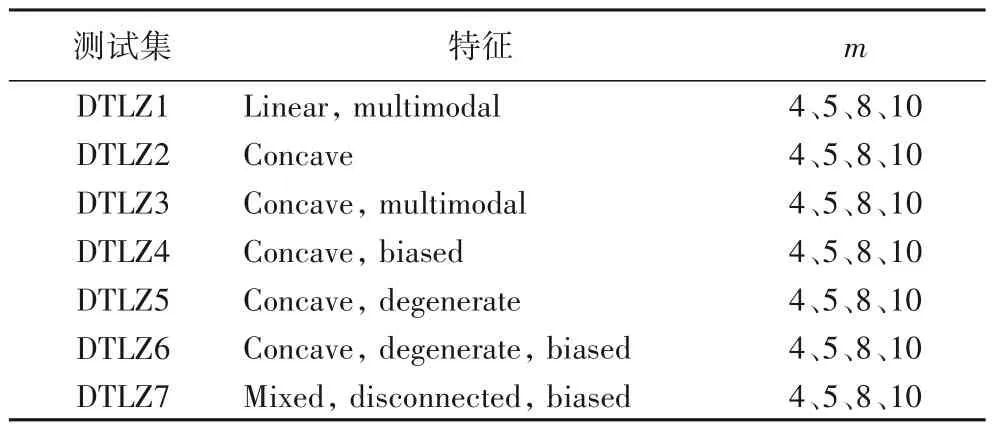
表1 DTLZ[1~7]测试集属性Tab.1 Attributes of DTLZ[1~7]test sets
3.1.2 评价指标
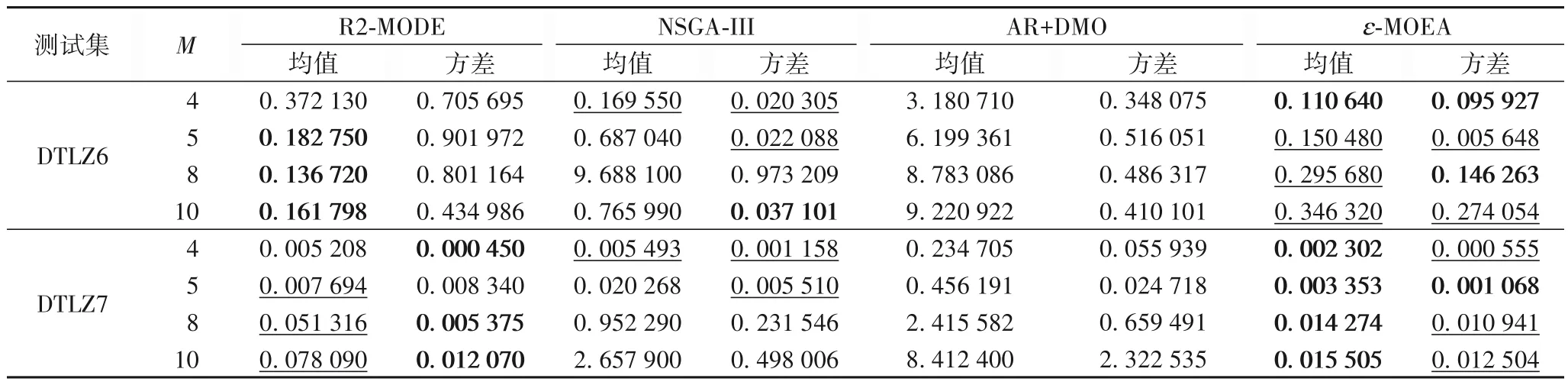
算法的性能指标由GD、IGD 和DM 来评估。GD 检验算法在优化过程中种群收敛的能力,值越小说明收敛性越好。DM衡量解集的分布性,取值在区间(0,1],DM值越大解集的均匀性越好。实验中需根据DM 针对的目标维数设置网格划分数,目标数4、5、8、10,相对的网格划分数为6、4、3、3。IGD 表示每个参考点到最近解的距离的平均值,值越小说明算法综合性能越好,整体效果更好。
3.1.3 参数设置
为保证算法的公正性,参考文献[20]对实验参数进行设置。
编码方式:实数编码。
交叉算子:模拟二进制交叉,分布指标ηc=20,交叉率等于1。
变异算子:多项式变异,分布指标ηm=20,变异率为1/n。每个算法独立重复实30次。种群规模N为100。
实验目标空间维数:4、5、8、10。
终止条件:需为不同测试函数设置相应的运行代数,DTLZ 1、DTLZ3、DTLZ6 迭代1 000 代;DTLZ2、DTLZ4、DTLZ5、DTLZ7迭代300代。
3.1.4 对比参数设置
对于ɛ-MOEA,需对不同测试函数的不同目标维数的ɛ参数[21]进行设置,参数设置如表2所示。
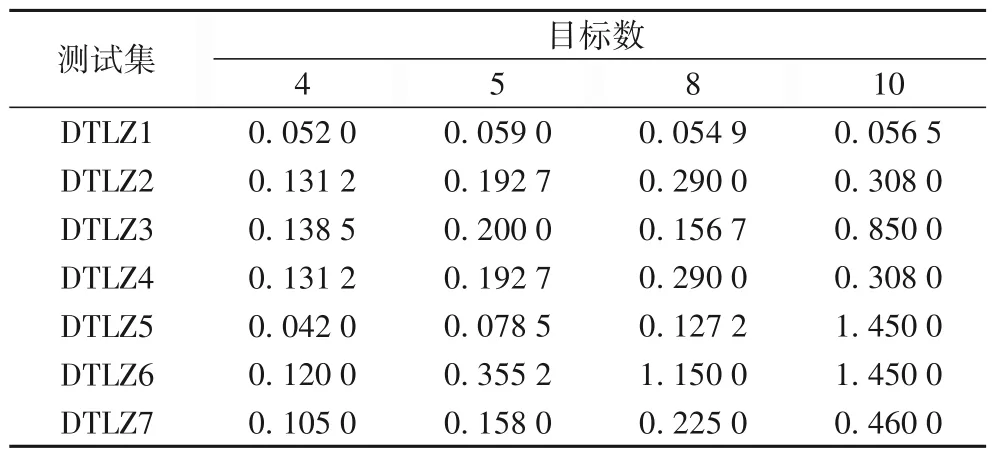
表2 ɛ-MOEA中ɛ参数设置Tab.2 Settings of ɛ parameter in ɛ-MOEA
3.1.5 结果对比分析
表3~5 分别给出了4 个算法在DTLZ 系列测试集上的均值和方差实验结果。
表3 给出了在4、5、8、10 维上的DTLZ[1~7]中的GD 值,其中R2-MODE 算法被加粗和加下划线数量明显多于其他算法,整体表现优秀,特别是在DTLZ2、DTLZ4、DTLZ5 问题上。ɛ-MOEA 次之,在DTLZ1、DTLZ3、DTLZ6、DTLZ7 表现较好。NSGA-III在更高维上完全不收敛。AR+DMO表现不理想。
表4 给出了在4、5、8、10 维上的DTLZ[1~7]中的DM 值,反映算法的分布性。R2-MODE 算法被加粗和加下划线数量显示其表现一般。分析原因认为,R2-MODE 算法含有一组均匀分布的权值向量和效用函数的R2贡献值,快速计算收敛性和多样性都较好的候选解;但算法仍然存在不足之处,比如在收敛困难的DTLZ3上表现得性能较弱,分析认为R2-MODE算法存在一定的不稳定性,由于算法前期主要考虑收敛性而造成种群在部分问题上收敛到局部PF 上,使得多样性管理不佳。ɛ-MOEA 总体表现较优,尤其在DTLZ5、DTLZ7 的高维处。NSGA-III 的收敛性较差,但其在DTLZ1、DTLZ2、DTLZ4上表现出了较好的分布性,体现了其自身算法的全局搜索能力。
GD 指标、DM 指标分别从算法的收敛性和分布性进行了验证,IGD指标进一步从算法的综合性进行评价。表5给出了在4、5、8、10维上的DTLZ[1~7]中的IGD值,R2-MODE算法被加粗和加下划线数量显示其综合性强,在DTLZ3、DTLZ4 和DTLZ6 上具有明显的优势,尤其在维数特别高时性能更加优越,在DTLZ 测试问题上取得了最为满意的结果。ɛ-MOEA 表现也较好,但ɛ需要根据不同维数、不同测试问题进行参数调整,实时性差。NSGA-III、AR+DMO 的综合能力不强。4 种算法综合性排序:R2-MODE、ɛ-MOEA、NSGA-III、AR+DMO。
3.2 系统实验分析
为测试R2-MODE 高维多目标算法的推荐选课系统的推荐教学效果,系统选用数据来源于全国一类本科高校,5 个学年、280 门课程、690 名学生、192 名教师、690 份学生评价、150份教师评价的记录数据。课程参数标准表、难度参数评价表、评价等级表,借鉴2019 年《普通高等学校本科专业目录》,以电子信息类基础专业为例,如表6~8所示。
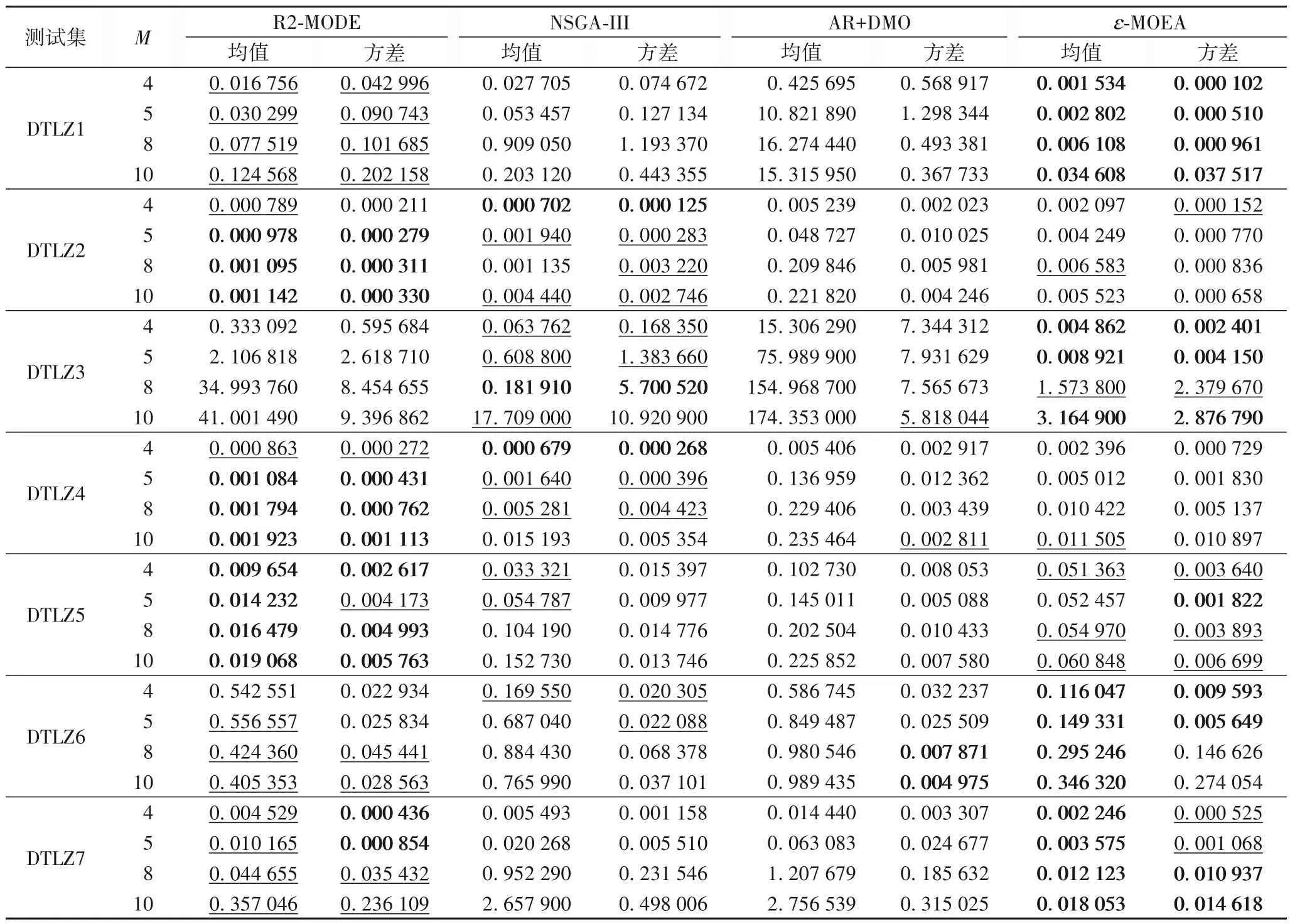
表3 GD指标的均值和方差Tab.3 Mean and variance of GD indicator
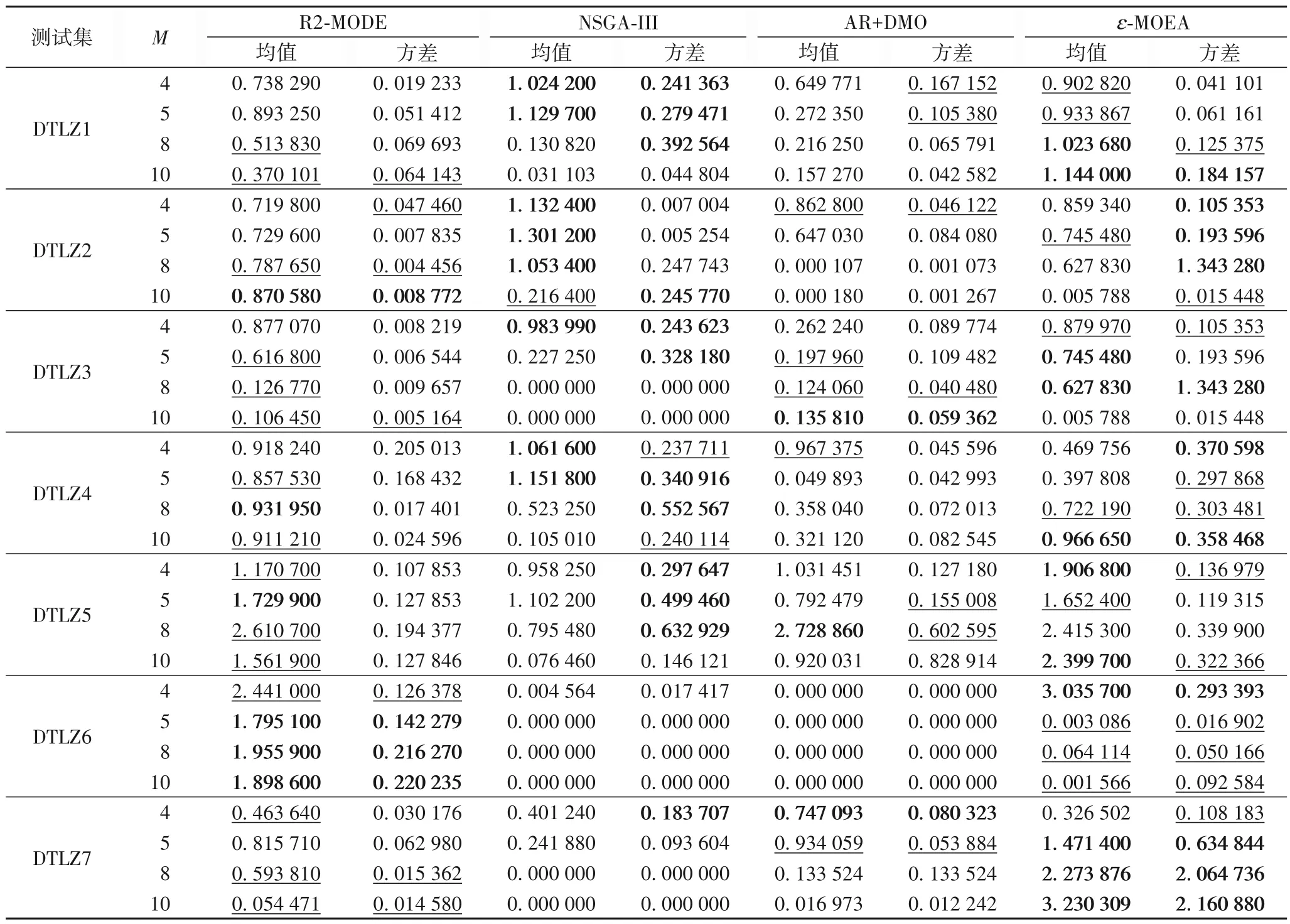
表4 DM指标的均值和方差Tab.4 Mean and variance of DM indicator
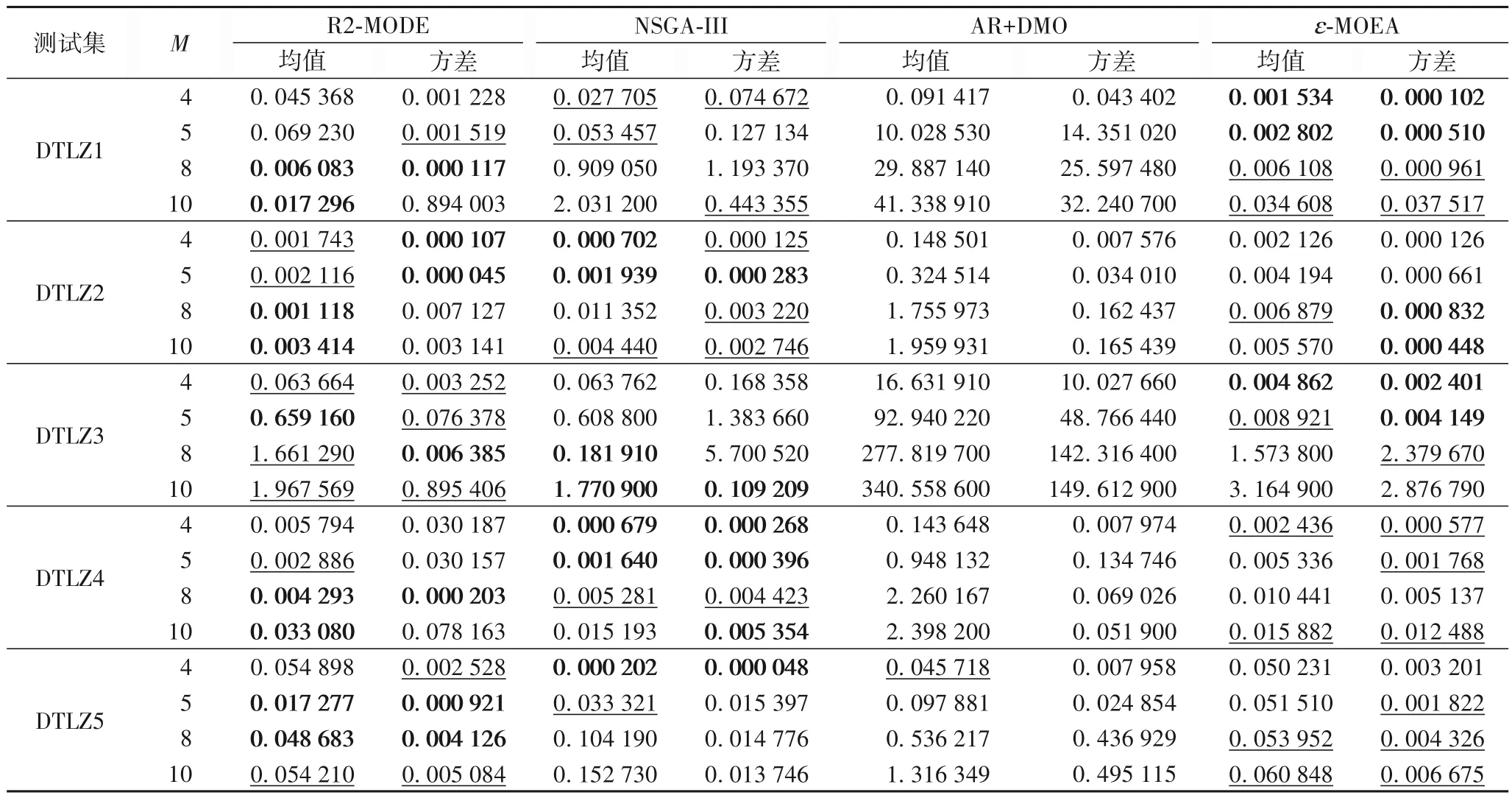
表5 IGD指标的均值和方差Tab.5 Mean and variance of IGD indicator
续表
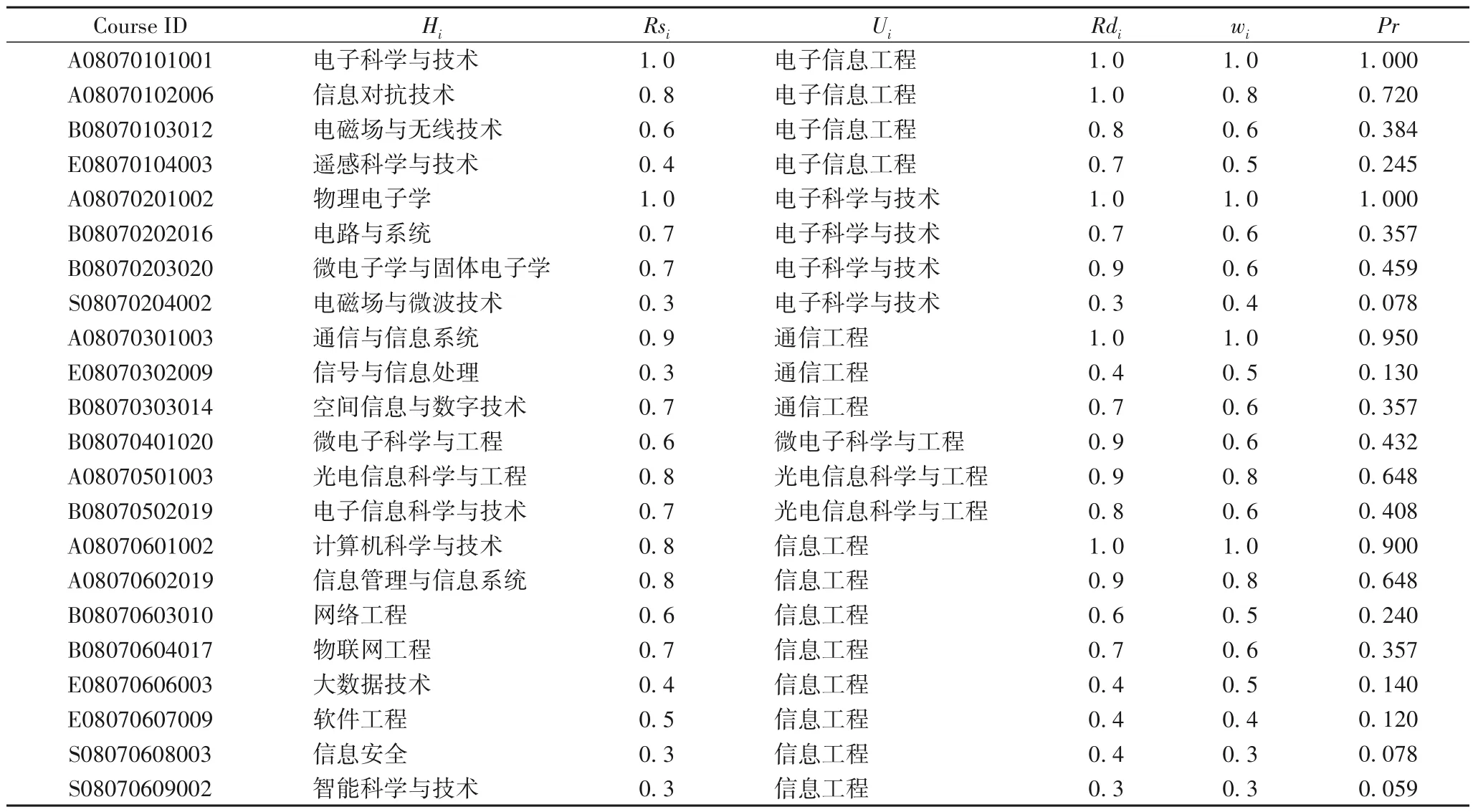
表6 课程参数标准表(部分)Tab.6 Course parameter standard table(part)

表7 难度参数评价表(部分)Tab.7 Evaluation of difficulty parameters table(part)
课程参数标准表6 中,Course ID 表示在一级学科下的子学科课程编码,共12 位,第1 位用表示课程专业属性,即主干课(A)、主干选修课(B)、选修课(E)、其他(S)。2~3 位表示学科门类,4~5 位表示专业代码,6~7 位表示是专业名称,8~9 位表示子学科名称,10~12 表示所在子学科内的课程。例如A08070101001表示如图3所示。
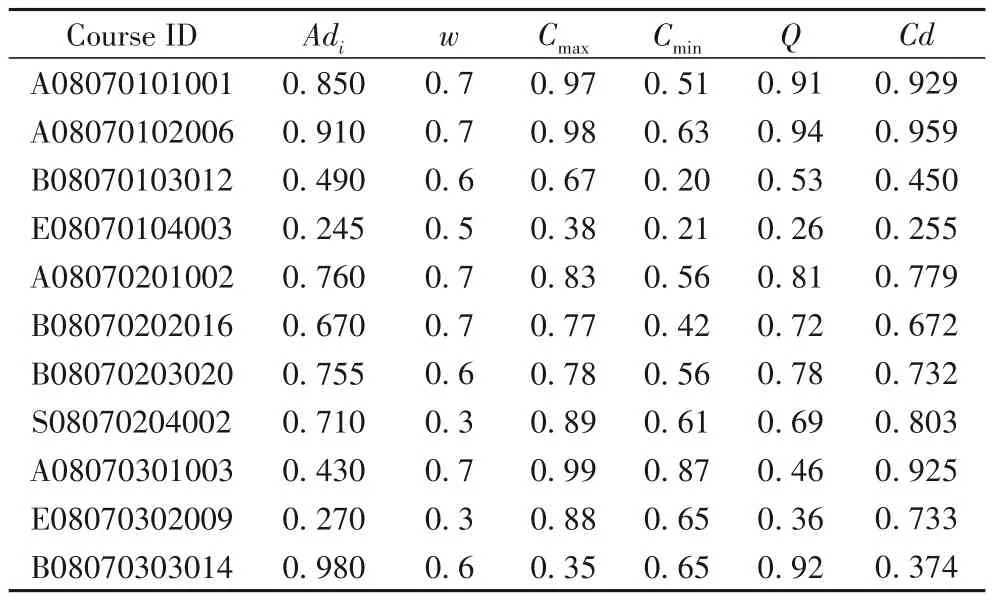
表8 课程评价等级表(部分)Tab.8 Grade of course evaluation table(part)
因为且存在C∈Hi∈Uq|C∈Hj∈Uq|C∈Up,如A08070101001 是电子科学与技术专业,Rdi、Rsi分别表示课程与一级学科、子学科的相关度,wi为课程专业权重值。由于篇幅有限,表6中只列出具有代表性课程信息。
难度参数评价表7中:Ce表示课程的综合评分;Pe为课程参与评价的年均分,取值大小由Tyn、Ten、Syn、Sen决定,专家教师和学生对课程综合评价的权重和为1。
课程评价等级表8中:Adi为问卷给出的难度值;Q表示课程的难度值,表示课程难度系数的指标Cd的结果给定课程的难度系数区间和网络投票问卷而来。网络投票问卷包含系统专家教师的问卷与完成课程学习的学生问卷,问卷量越能更反映真实的情况。专家教师和学生对课程给出难度值的权重和为1。
课程教师信息表9中:Rti的值由ri界定,ri表示在课程主讲教师的第i个专业与所授课程的相关性,Rti取值由系统专家在考核课程主讲教师时在系统内设定初始值。

图3 课程参数示例Fig.3 Example of course parameter
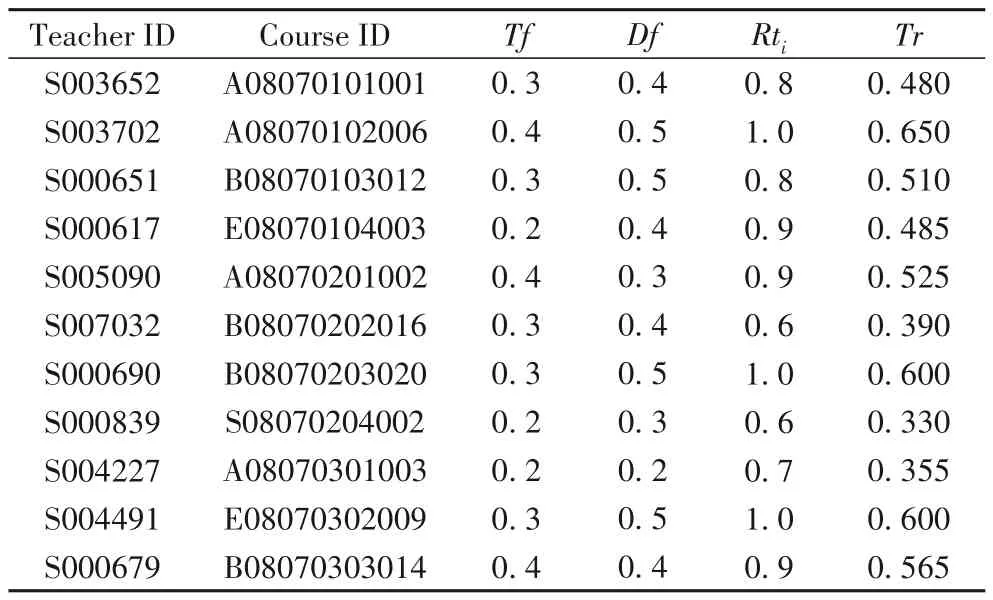
表9 课程教师信息表(部分)Tab.9 Course teacher information table(part)
在1.2 节建立的多目标推荐式课程系统模型中,系统初始选定方向、子方向以及已学课程,利用R2-MODE 高维多目标算法对模型进行求解,确定4 目标最优的选课方案,优化加权切比雪夫权值向量λ=(λ1,λ2,…,λk)∈Λ,实现课程教师专业度Tr、专业相关度Pr、课程难度系数Cd、课程综合评价Ce共4 项推荐评价指标的同时最优化。R2-MODE 算法中种群规模NP 取值为30,最大迭代次数Gen取值200,MODE 算法中,变异因子F取值0.5,交叉因子CR取值0.4。表10所示为在选择工科→信息工程→物联网专业后,R2-MODE 算法对多目标课程引导教学模型的求解选课结果。多目标优化问题最终需要得到全局最优解集,而非单个最优解,因而在结果集中选取10 项互为非支配的最优解,代表多目标课程引导教学系统中最优的10 项设置选课参数的方案。均匀分布的权值λ1、λ2、λ3、λ4作为选课者4目标的偏好信息。
4 结语
从现有网络平台缺乏精准引导式课程选择的问题出发,提出了一种多目标课程引导教学模型。通过引导式决策选课实现对课程教师专业度、课程的专业相关度、课程难度系数、课程综合评价等多项性能的同时最优化。为得到以人为本的、精准的高维多目标,设计了基于R2 指标的优化MODE 算法,提高了收敛精度和解集的分布性。成功针对学生个体的特征、意愿,建立实现课程的精准推荐,为智能选课提供了一种新的方法。系统实验结果表明,设计方法在数据集的收敛性和分布性上都能得到较优的结果,为网络平台精准引导式课程选择提供了必要的理论支持。
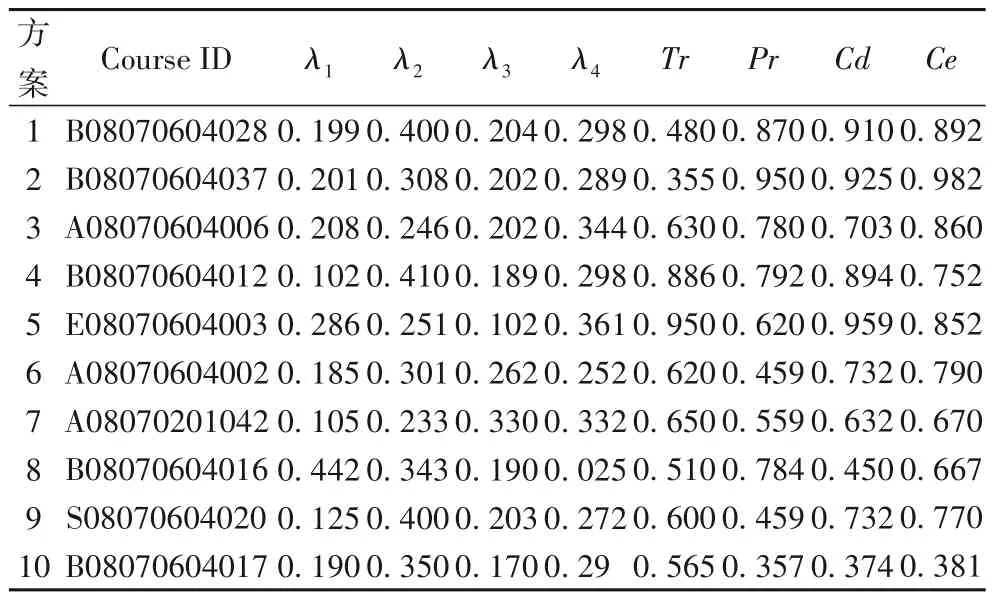
表10 课程选择结果Tab.10 Results of course selection
