面向大数据任务的调度方法
2020-10-18李孜颖石振国
李孜颖,石振国
(南通大学信息科学技术学院,江苏南通 226001)
(*通信作者电子邮箱chinaemail@sohu.com)
0 引言
随着近些年数据爆发式的增长,越来越多的人将注意力集中到了大数据领域。大数据具有容量巨大、种类繁多、来源复杂、价值密度低等特征[1],对此,市面上也出现了很多通用底层大数据系统来处理大数据,如Hadoop、Spark 等[2]。然而对于多数大数据系统,内部任务的划分标准不一,对大数据任务资源的分配也缺乏一定合理性,大数据任务处理流程存在不规范的问题。因此,本文将任务调度理论引入到大数据任务处理中,帮助建立合理的大数据任务管理体系,从而规范大数据任务处理流程,提高大数据任务处理效率。
调度即是一种时间、空间上的排序。例如车站对班车的排班是一种调度,操作系统将进程提交给中央处理器(Central Processing Unit,CPU)也是一种调度。大数据的处理过程也可以看作是一种任务调度,即根据实际的大数据任务和资源情况,将资源分配给相应的大数据任务加以执行的过程,而任务调度的关键则在于如何精准地划分任务以及合理高效地为任务分配资源。
任务调度问题在许多不同领域中都有一定的研究[3-9]。例如,文献[7]针对广域信息管理系统,提出一种多服务质量(Quality of Service,QoS)约束条件的蚁群优化任务调度算法;文献[8]针对移动云计算中有向无环图(Directed Acyclic Graph,DAG)模型的任务调度问题,提出了一种能效任务调度算法;文献[9]针对对等网络环境,提出一种能有效利用网络资源的基于相似度的任务调度算法等。
上述文献均是对任务调度问题的研究,但将任务调度理论与大数据相结合还不多见。本文将大数据任务的处理看作是一种任务调度,并以此为基础,提出一种面向大数据任务的调度方法模型。本文工作主要有:
1)针对大数据任务划分标准不统一、处理流程不规范的问题,在大数据任务处理中引入任务调度理论,建立合理的任务管理体系,精准划分任务,规范任务流程,提高大数据处理效率。
2)针对大数据容量巨大、种类和来源复杂、噪声多的问题,引入粗糙集中的决策表属性约简方法,提出一种基于互信息的大数据决策表约简模型,从而减少大数据分析任务的数据量,提高大数据分析效率。
3)针对大数据任务资源分配缺乏一定合理性的问题,引入模糊数学中的模糊综合评价方法,将模糊综合评价的结果作为对任务分配资源的依据,提高任务资源分配合理性。
4)针对大数据任务的处理,提出一种面向大数据任务的调度方法模型,并给出算法具体流程和步骤,从而实现对大数据任务的调度。
5)将所提出的面向大数据任务的调度方法模型应用在实际数据集中测试,并对测试结果进行分析;实验结果表明,该调度模型能够有效提高处理大数据任务的效率。
1 大数据任务分析及处理方法
1.1 大数据任务分析
在现代主流的大数据系统中,大数据任务通常用DAG 表示[10],其中顶点是大数据任务,连接顶点的边是大数据任务之间的关系。不可避免的,大数据任务间要共享集群资源,对此,按照什么样的标准划分大数据任务并为其分配资源就成为了一个十分重要的问题。
在现代大数据系统中,通常可将大数据任务分为四大类,即数据采集、数据处理与集成、数据分析以及数据解释[11]。在大数据处理的过程中,由于经过数据采集任务所得到的数据,其数据结构各不相同,因此需要对采集到的数据处理成统一标准格式的数据,并将处理后的数据进行存储。数据完成预处理任务后,需要选用合适的数据分析方法对这些处理过的数据进行分析,并通过可视化等技术,将数据分析的结果向用户展示。
1.2 决策表的相关概念
决策表是用来描述和分析过程化决策情形的一种表格状表示方式[12]。在决策表中,以行、列的形式来描述和表示决策规则和知识信息。决策表概念的系统化定义如下。
定理1设ai(i=1,2,…,m)表示可供选择的决策行为,AS是ai的集合。θkj(j=1,2,…,n)是一个逻辑表达式,Sj表示θkj的集合。用xij表示实施决策ai后,自然状态是θj的决策结果,xij={0,1}。决策表DT即可用来表示一个从θj到xij的映射。由定理1 可知,一个决策结果在决策表模型中是由一个或多个Sj表示的,即每一个xij对应输入的不同Sj,不同的Sj会形成不同的xij。
在定理1 所述经典决策表模型中,只有行为和结果,对于一些复杂的系统,往往有多种不同的行为同时起作用,在这种情况下,不能仅仅考虑行为与结果,对此,有带权重的决策表模型[13]如下:
定理2设Ai(i=1,2,…,m)表示可供选择的第i个决策行为集,Sj(j=1,2,…,n)表示第j个结果集。用Xij表示决策集Ai对结果集Sj的权重集,且
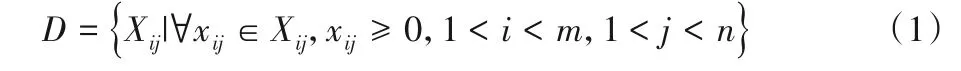


引入变量P[j]表示各结果集发生的可能性,则

设阈值为q,则

1.3 基于互信息的大数据决策表约简模型
属性约简又称知识约简,是指为了保留最小属性数的特征子集,在不改变知识库分类能力的前提下,删除冗余知识的过程[14]。当前数据库系统通常可以对数据进行插入、查找、分类等操作,但是想要知晓数据间到底有着怎样的内在联系却很困难,而属性约简可以更好地帮助发现数据其中的联系[15-19]。
在决策表中,为了了解各种条件属性对于决策重要性的影响,可以计算条件属性与决策属性间的互信息[20],因此可以利用互信息对决策表进行属性约简。
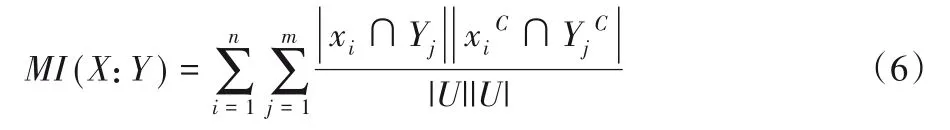
根据式(6),可通过计算决策属性D与条件属性a之间互信息的大小,来衡量条件属性对于决策的重要性。互信息值越大,该属性对于决策起到的重要性也就越大。对于决策表的约简,有下述定理:
定理3在相容决策表DT中,A⊆C,当且仅当MI(D:C)=MI(D:A)时,A是C相对于决策属性集D的一个约简,且A相对于D是独立的。[22]
根据定理3,本文提出基于互信息的大数据决策表约简算法,算法从初始的条件属性集开始,循环并逐步删去冗余属性。本文算法具体步骤如下:
输出DT的约简结果AR。
Step1 计算DT的互信息MI(D:C)。
Step2 从C中随机选取一个条件属性ai,计算出对于每一个ai∈C,其互信息MI(D:{ai})的值,并按照升序进行排列。
Step3 令AR=DT,重复以下操作直至循环结束:
Step3.1 计算MI(D:AR-{ai})的值。
Step3.2 如果MI(D:C)=MI(D:AR-{ai}),ai可约简,令AR=AR-{ai};反之,ai不可约简,AR不变。
Step4 循环结束,得到约简结果AR。
1.4 模糊综合评价法
在模糊数学的所有综合评价法之中,模糊综合评价法是常用的一种方法。根据模糊数学中的隶属度原理,模糊综合评价法可以将对事物的定性评价转变成对事物的定量评价,因此该方法也经常用于为受到多种因素影响的事物进行全面的综合评价[23]。
针对大数据任务调度系统,任务的调度结果也是受多种因素影响,具有不确定性和模糊性,因此可用模糊综合评价法来对任务进行分类,将对任务评价的结果作为对任务进行调度的结果。
模糊综合评价步骤[24]如下:
1)确定评价对象。
2)确定评价指标集U。
评价指标集是指评价者对被评价对象进行评价所依照的评价指标的集合,可能会存在多级指标,且U={u1,u2,…,un}。
3)确定评价等级(评语集)V。
不同的评价者对不同的评价对象可能会有不同的评价等级。评语集就是这些所有可能的评价结果的集合。且V={v1,v2,…,vm}。
4)确定评价指标的权重W。
各评价指标的权重大小,反映了各评价指标对于评价结果的重要程度大小。由于各评价指标权重大小的不同,可能导致最终得到的评价结果差异很大,因此如何确定评价指标的权重是模糊综合评价中至为关键的一步。权重W=(w1,w2,…,wn),且各评价因素的权重总和为1,即1(wi>0)。
常用的确定权重的方法主要有德尔菲法确定权重法、层次分析(Analytic Hierarchy Process,AHP)确定权重法、熵值确定权重法等。
德尔菲法确定权重法[25]是根据专家的知识、经验、综合分析能力等,对各项评价指标判断、分析并为其赋予权值,该方法是最常用的确定权重方法。
将定性与定量相结合是AHP[26]的特点,核心是定量描述决策者的经验和判断,增强决策依据,提高决策准确性。为综合计算各指标的权重系数,AHP建立了等级评价指标体系,根据同等级的指标直接相对重要性来衡量。
熵值确定权重法[27]是一种客观的赋权法,通过对各项指标进行观测,并根据所观测得到的信息大小确定各项指标权重。信息熵是信息论中对信息的不确定性的一种量化度量,信息熵公式为

其中:p表示随机变量x的输出概率。通过式(7)可以看出,信息量越大,变量x的不确定性越小,信息熵也就越小;反之亦然。因此可以使用信息熵来衡量各指标的变异程度,从而计算出各项指标的权重。
针对大数据任务,采用层次分析法AHP 确定各评价指标的权重。
5)建立模糊关系矩阵R。
单因素模糊评价[28]即逐个对被评事物依据评价指标集U进行量化,也就是得到评价对象ui(i=1,2,…,n)对每个评价结果的隶属度(R|ui),进而可以得到模糊关系矩阵R,即
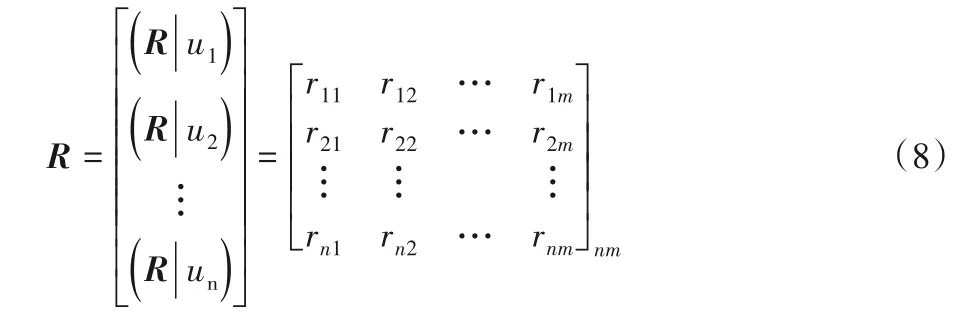
6)合成模糊综合评价结果矢量。
对多个评价指标进行综合评价,选用适当的模糊合成算子,将模糊权重W与各被评事物的模糊关系矩阵R进行合成,可以得到各被评价事物的模糊综合评价结果矢量B,且

常见的模糊合成算子有M(∧,∨)、M(·,∨)、M(∧,⊕)、M(·,⊕)四种[23],这四种算子的特点如表1所示。

表1 四种模糊合成算子的特点Tab.1 Features of four fuzzy synthetic operators
针对大数据任务的特性,采用加权平均型的模糊合成算子M(·,⊕),对于多个被评价对象,可以依据其等级位置进行排序。
2 面向大数据任务的调度方法模型
2.1 任务调度模型原理
由于历史调度任务中,资源使用情况以及执行时间均已知。根据K近邻思想[29],对于输入的新实例,若在训练集中能找到与该实例最相邻的k个实例,并且这些实例多数属于某个类,就把该输入的新实例分类到这个类中。若两个任务数据集的模糊综合评价结果相近,可以认为这两个任务数据集的资源使用情况以及执行时间也相近。
当要执行新的大数据任务数据集时,先对其进行属性约简,再对其进行模糊综合评价,根据评价结果调度分配资源。该流程如图1所示。

图1 调度策略流程Fig.1 Scheduling strategy flowchart
2.2 任务调度模型算法
有n个历史任务的数据集DS={DS1,DS2,…,DSn}
Step1 对DS进行属性约简,得到约简后的结果DS′;对DS′进行模糊综合评价,得到评价后的结果DS″={DS"1,DS"2,…,DS"n}。
Step2 输入新任务P,对P进行属性约简,得到约简后的结果Q。
Step3 对Q进行模糊综合评价,得到评价结果B。
Step4 遍历DS″,找出与B最为相近的DSj"。
Step5 根据DSj"的历史资源分配和历史任务执行情况生成工作流,预估并为P分配资源。
3 实验与结果分析
3.1 实验过程
为评估本文所提出的算法,采用基于Apache Hadoop平台的Oozie[30]框架进行任务调度。
实验选取UCI(University of California Irvine)[31]数据库中的10 个数据集,将其中70%的数据集用作训练数据集,30%的数据集用作测试数据集。通过所提出的基于互信息的属性约简方法对UCI 数据集进行属性约简,之后对属性约简后的数据集进行模糊综合评价,以模糊综合评价结果在测试集上预测的实际表现来评估本文算法。实验所选取的数据集信息如表2所示,其中:m表示约简前的条件属性个数,M表示约简后的条件属性个数。
将各数据集的样本数u1、类别数u2、约简后的条件属性数u3、数据集要执行的任务类型u4作为评价对象,即指标集U={u1,u2,u3,u4}。将各数据集与历史调度任务数据集的相似度1~5 作为评语集,其中5 表示最为相似,1 表示最不相似,即评语集V={1,2,3,4,5}。对U中的每一个ui做单因素判断,确定ui对每个评价结果的隶属度(R|ui),进而确定模糊关系矩阵R,即各数据集从不同的单指标来看对各等级模糊子集的隶属程度。
单因素评价获得模糊关系矩阵后,为评价指标集中的各个指标在评价目标中的不同地位和作用,在控制实验样本和实验环境不变的前提下,各评价因素的权值变化如图2 所示,得到各评价因素的最优权值W=(0.1,0.1,0.2,0.6)。
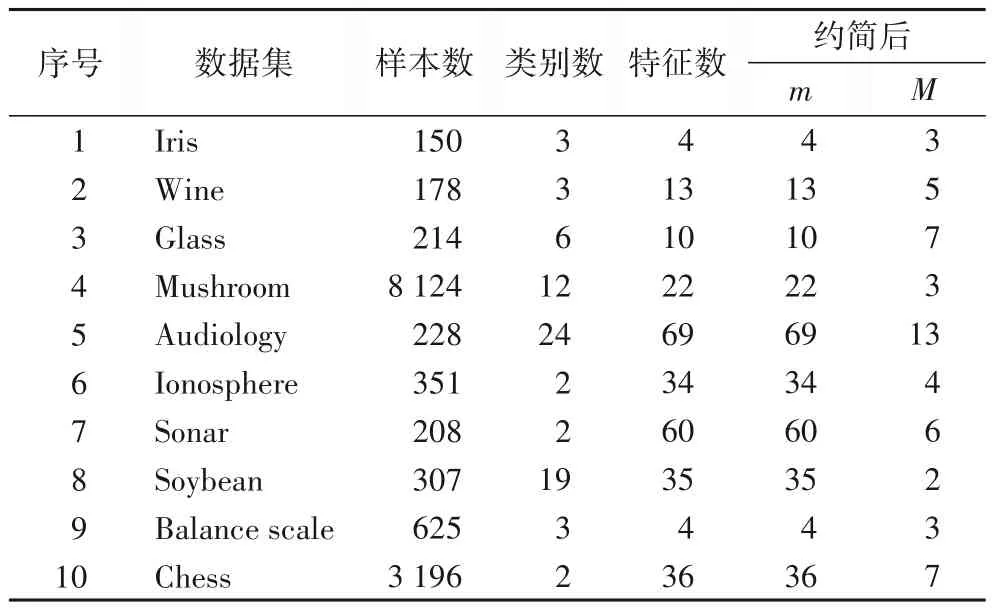
表2 实验所用数据集信息Tab.2 Information of datasets used in experiments
用W对R中不同的行进行综合,得到该被评事物从总体上来看对各等级模糊子集的隶属程度,即模糊综合评价结果向量B。以B的结果为基础,生成工作流并提交给Oozie 进行调度。

图2 各评价因素的权值变化Fig.2 Weight changes of different evaluation factors
3.2 实验结果与分析
为评估本文算法效果,将朴素贝叶斯(Naive Bayes,NB)算法、误差反向传播(error Back Propagation,BP)算法、均方根传递(Root Mean Square Prop,RMSProp)算法与本文算法进行对比。其中:NB 算法是一种利用概率统计进行分类的算法;BP 算法是一种按照误差逆向传播算法训练的多层前馈神经网络算法,在实际中被广泛采用;RMSProp算法加入衰减系数控制历史信息获取,是一种有效且实用的神经网络优化算法。不同算法的预测准确度对比实验结果如表3所示。
整体来看,本文算法在平均预测准确度上比NB 算法高7.42 个百分点,比BP 算法高5.16 个百分点,比RMSProp 算法高3.74 个百分点,这是由于属性约简保留了最小属性数的特征子集,在不改变知识库分类能力的同时,去除了数据集中的噪声,从而提高了预测精度。结合不同的数据集分析,对于特征数较少的数据集如Iris、Balance scale,本文算法的预测精度略高于其他三种;对于特征数较多的数据集如Ionosphere、Sonar等,本文算法较其他算法在预测精度上有显著提高。
为评估本文所提调度算法性能,将HCPFS(Heterogeneous Critcal Path First Synthesis)算法[32]和HIPLTS(Heterogeneous Improved Priority List for Task Scheduling)算法[33]与本文算法进行对比。采用调度长度下界比(Schedule Length Ratio,SLR)、加速比作为算法评估指标,SLR和加速比sr的计算公式如下所示:
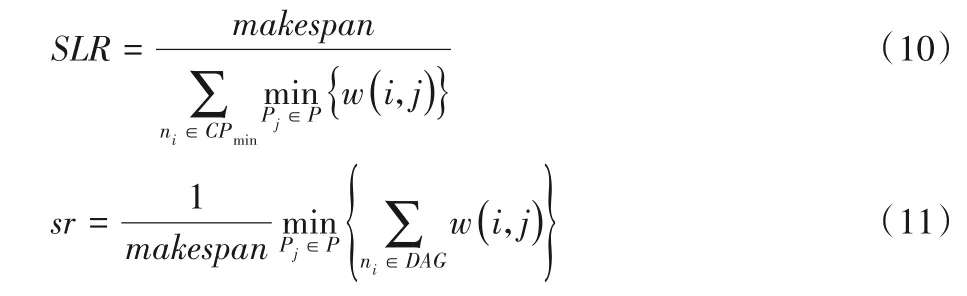

表3 不同算法的预测准确度对比实验结果 单位:%Tab.3 Experimental results comparison of prediction accuracy by different algorithms unit:%
使用Oozie 按照文献[34]提供的方法生成随机任务图。具体设置参数如下:
1)节点数nodes={20,30,40,50,60,70,80,90,100};
2)节点出度outdegree={1,2,5,20};
3)通信计算比(Communication to Computation Ratio,CCR),CCR={0.1,0.2,0.5,1,2,5,10};
4)图形状参数α={0.5,1.0,2.0};
5)处理器计算开销β={0.1,0.2,0.25,0.5,0.6,0.75,1}。
三种调度算法平均SLR和平均sr的实验对比结果如图3所示。
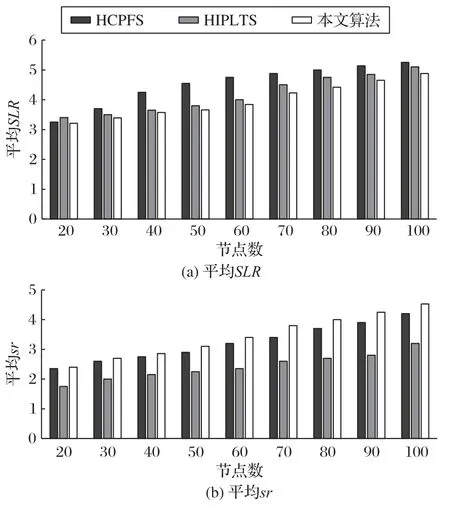
图3 三种调度算法平均SLR和sr的实验对比结果Fig.3 Experimental results comparison of average SLR and sr by three scheduling algorithms
通过实验数据可以看出,相较于HCPFS 算法和HIPLTS算法,本文算法的平均SLR分别下降了12.14%和4.56%,平均sr分别提升了7.14%和42.56%,说明本文算法具有更好的任务调度性能,能够有效提高任务调度效率。
4 结语
针对大数据处理流程中如何合理高效分配资源的问题,本文引入任务调度理论,提出了一种面向大数据任务的调度方法。该方法结合粗糙集理论,引入决策表模型进行属性约简,从而去除不重要和冗余属性以保持知识分类的不变,提高大数据任务处理的效率;同时引入模糊综合评价方法,将模糊综合评价结果作为对任务进行调度的依据,提高任务资源分配合理性。通过在UCI 数据集上的实验结果分析表明,该算法能有效提高预测精度;通过与HCPFS 算法和HIPLTS 算法实验对比,表明本文算法能有效提高大数据系统中任务调度的效率。接下来的工作是考虑使用机器学习方法进行模糊综合评价,优化算法生成工作流的流程,提高算法性能。
