基于随机场和数学形态学的水泥基材料三维孔隙结构建模研究

曹金成，张 翔

(云南大学建筑与规划学院，昆明 650504)

0 引 言

水泥基材料是土木工程领域中用量最大且应用最广泛的建筑材料之一。作为非连续多孔介质，水泥基材料的渗流和力学性质与孔隙率和孔径分布等孔隙结构特征密切相关[1]。基质与孔隙网络在微观或纳观尺度的特征决定了材料在宏观尺度的力学响应[2-3]。因此，研究水泥基材料的三维孔隙结构有助于更透彻地了解其特性。

通过直接扫描技术可以从试样中获得水泥基材料孔隙结构的真实图像。胡曙光[4]、王培铭[5]等通过BSE-IA技术得到了水泥基材料的背散射图像并在此基础上分别进行了孔隙率测定与物相分析。严辰成等[6]利用X-CT技术获取了水泥砂浆的孔隙图像并重构了其三维孔隙结构。直接扫描技术极大推动了水泥基材料的研究进程，但也存在一些不足。例如BSE-IA技术需要对试件进行预先处理，从而破坏了试件的微观结构。X-CT技术虽无需对待测试件进行预处理，却受到分辨率、信噪比与灰度值划分等因素的影响，使得扫描尺度受到限制，物相划分造成差异，无法对试件进行精确的定量计算[7]。FIB、SEM、TEM等直接扫描技术虽具备更好的扫描性能和更高的放大倍数，所成图像也更为精准，但相应的试验成本与时间也更多。

如今对水泥基材料孔隙结构进行建模已成为研究其物理及力学性质的一种有效手段。在以往的研究中，多数针对水泥基材料的建模都需要基于具有特定几何形状的简单单元，如:Ye等[8]对水泥材料水化的研究和田梦云[9]对混凝土单轴力学性能的研究中，材料建模时都将骨料颗粒假定为球体单元；王飞阳等[10]研究裂缝对混凝土结构力学性质的影响时构建了骨料为椭圆形单元的模型；Ranaivomanana[11]和Varloteaux[12]等在对水泥基材料进行建模时，分别使用了圆柱体单元以及通过圆柱形通道连接的球单元。基于简单单元建模的方法能够保证模型的孔隙率，但无法在模型中呈现出水泥基材料中基质和孔隙网络形态与空间分布的随机性。

本研究着力于构建满足材料孔隙特征(孔隙率、孔径分布)且具有随机形态的水泥基材料三维孔隙结构模型。采用偏移集理论将连续分布的高斯随机场转化为具有随机形态的二相场来代表材料的基质和孔隙，通过多个二相场联合完成模型构建；采用数学形态学图像处理方法进行分析，结果验证了该方法构建出了满足材料试验孔径分布曲线的孔隙结构。Zhang等[13-14]在对饱和岩石气体运移及突破的研究中，使用此方法构建了黏土岩模型，且在后续基于此模型的力学分析中获得了与试验数据较为接近的模拟结果。本文以水灰比为0.64的水泥浆为研究对象，陈述建模过程，展示建模结果，然后基于该模型分析水泥基材料的力学和渗流特性。

1 建模方法

1.1 高斯随机场和偏移集理论

对连续分布的高斯随机场设定阈值，二相化处理之后可以用于模拟孔隙介质中具有随机形态的孔隙网络和基质部分[14]。对于满足标准正态分布(期望为0，标准差为1)的高斯随机场f(x)而言，场内两个随机点的协方差方程C(h)可以采用相关长度来定义，即：

(1)

式中：h代表两点的空间距离；Lc(Correlation Length)代表相关长度。随机场中任意两点间距离越近则相关性越强，距离越远则相关性越弱，而相关长度代表了使场中任意两点间存在相关性的最小距离[15]。因此，随机场的相关长度越大，说明场内具有相关性的点的范围越大，场的波动越小，反之则波动越大。如图1所示，大相关长度使场的形态平滑，小相关长度使场的形态起伏。

图1 高斯随机场中相关长度对场形态的影响[16]Fig.1 Influence of correlation length on field shape in Gaussian random field[16]

对于某个定义在范围K内的随机场f(x)，如图2所示，对该随机场设定一个阈值t，偏移集Es(Excursion Set)定义为f(x)中大于t的部分，即：

图2 一维情况中的偏移集理论Fig.2 Excursion set theory in one-dimensional case

Es≜{x∈K|f(x)≥t}

(2)

若将一维情况扩展到三维，并将随机场中的偏移集Es视为一相，Es之外的其他部分视为另一相，如图3所示，阈值化处理之后，三维连续场转化为离散的二相场。

图3 高斯随机场转化为二相场Fig.3 Gaussian random field transforms into binary field

定义的阈值t的大小控制了二相的相对比例，因此可以在阈值化后的二相场形态上发挥重要作用。假设偏移集Es代表多孔介质中的孔隙，随机场余下部分代表基质。阈值t降低，对应Es所占比例增加，孔隙率增加。相反的，阈值t增加使孔隙率降低。通过模型研究，孔隙率φ与阈值t的关系可表达为：

(3)

结合上文结果可知，相关长度可以控制随机场形态的起伏，因此降低相关长度，场内具有相关性的点的范围变小，随机场波动增大，阈值化后各相的形态变得狭窄。通过调整阈值与相关长度两个参数的取值可以生成不同形态的孔隙结构模型，如图4所示。较大的相关长度和阈值使得孔隙大而少，较小的相关长度和阈值使得孔隙小而多。

图4 阈值和相关长度变化时生成不同形态的孔隙结构模型Fig.4 Various sorts of pore structure model through the variation of threshold and correlation length

1.2 偏移集联合

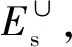
(4)

图5为两个具有不同相关长度的偏移集联合的结果，其中黑色代表基质，灰色代表孔隙。

图5 不同相关长度偏移集的联合Fig.5 Union of excursions with different correlation lengths

由于联合之后孔隙部分有重叠，导致合集的总体积分数不等于单个偏移集的体积分数之和(相比较小)，即：

(5)

(6)

(7)

(8)

2 建模与验证

2.1 材料选取

建模对象选取水灰比为0.64的水泥浆。有关水泥浆的孔隙率和孔径分布等孔隙特征已有较多研究成果，多数采用压汞法获得[18-20]，但压汞法仅能对开孔隙进行孔径分布研究，闭孔隙的特征则依赖于直接扫描技术。本研究中建模所用到的水泥浆孔径分布规律如图6所示，为Song等[21]基于FIB/SEM图像采用统计学反演获得的成果。水灰比为0.64的水泥浆孔径主要分布在0.02～0.20 μm范围内，孔隙率为16.1%。

图6 水灰比为0.64的水泥浆累积孔径分布曲线[21]Fig.6 Cumulative pore size distribution curve of cement paste with water-cement ratio of 0.64[21]

2.2 建 模

模型构建在边长为3 μm的立方体内，网格划分为300×300×300，最小单元尺寸为0.01 μm，因此可以在该立方体内呈现出W/C=0.64的水泥浆的主体孔隙部分(0.02～0.20 μm)。对图6中累积孔径分布曲线进行分析，孔隙模型通过6个相关长度分别为0.02 μm、0.04 μm、0.06 μm、0.08 μm、0.10 μm、0.20 μm的二相场联合而成，各场设定的孔隙率分别为2.0%、4.0%、2.5%、3.5%、3.0%、1.1%，总孔隙率为16.1%，生成的各场的孔隙率分别为2.29%、4.47%、2.59%、3.63%、3.18%、1.34%，联合后的模型总孔隙率为16.3%，相关参数如表1所示，生成的模型如图7所示。

表1 水泥浆孔隙结构建模相关参数(W/C=0.64)Table 1 Related parameters for the generation of cement paste pore structure model (W/C=0.64)

图7 生成的水泥浆孔隙结构模型(W/C=0.64，黑色为基质，灰色为孔隙)Fig.7 Generated cement paste pore structure model (W/C=0.64, black color represents the matrix, gray color represents the pore space)

2.3 构建方法及模型验证

在满足孔隙率的前提下，还需要探讨模型的孔径分布。本研究采用数学形态学图像处理方法来对模型进行孔隙网络尺寸筛分。

数学形态学(Mathematical Morphology)是以格论和拓扑学为基础的分析和处理几何结构的理论和技术，主要用于图像处理[22-25]。其运算过程是将初始图像通过与一定形状和大小的“探针”(称为结构元素)相互作用从而将初始图像转变为一个新的图像[26-27]。结构元素的尺寸控制着运算的结果[28]，结构元素形状的选择没有理论上的限制，为了获得更准确的结果，应使用与要分析的形状相似的单元。对于空间曲面构成的孔隙网络，结构元素定义为类似于球体的八面体[13]。数学形态学的基本运算包括腐蚀、膨胀、开运算、闭运算等，本研究中孔隙尺寸筛选用的是开运算。

开运算由腐蚀和膨胀两个基本步骤结合而成[29]。如定义一个尺寸为d的结构元素，待处理图像如图8(a)中不规则形状部分所示，腐蚀运算中图像与结构元素的交互可简单理解为将图像沿边界等尺寸收缩d/2的宽度，则原图中尺寸小于d的部分将被剔除，如图8(b)所示。基于腐蚀处理后的图像，进行膨胀，相应地可理解为使图像沿边界等尺寸延伸d/2的宽度，则在腐蚀运算中缩小并保留下来的部分可以得到重建，如图8(c)所示。开运算的过程可定义为：

图8 形态学开运算[14]Fig.8 Morphological opening[14]

M∘E=(M⊖E)⊕E

(9)

式中：M为待处理图像；E为结构元素；∘为开运算；⊖为腐蚀运算；⊕为膨胀运算。通过开运算处理后，原图中尺寸小于等于结构元素的部分将被剔除。

将所建水泥浆孔隙结构模型中的孔隙网络视为待处理图像，进行一系列结构元素尺寸逐渐增大的开运算，模型中保留的孔隙将逐渐减少。W/C=0.64的水泥浆孔隙结构模型的开运算过程如图9所示，对生成模型进行结构元素为50 nm的开运算之后，尺寸小于等于50 nm的孔隙将被剔除；对生成模型进行结构元素为110 nm的开运算之后，仅有尺寸大于110 nm的孔隙得以保留。就像颗粒筛分试验中不同孔径的筛子可以筛选出粒径大于不同孔径的颗粒一样，不同结构元素尺寸的开运算可以筛选出尺寸大于不同结构元素的孔隙。

图9 W/C=0.64的水泥浆孔隙结构模型的开运算过程Fig.9 Morphological opening operations on the generated cement paste pore structure model (W/C=0.64)

在模型的主要孔隙尺寸区间0.02～0.20 μm内，从小到大依次选择多个结构元素尺寸进行开运算，每次开运算后统计残余的孔隙率，则可以得到模型的累积孔径分布曲线，并与试验数据进行比较，如图10所示。比较分析可知，构建的W/C=0.64的水泥浆三维孔隙结构模型较好地还原了孔径分布。

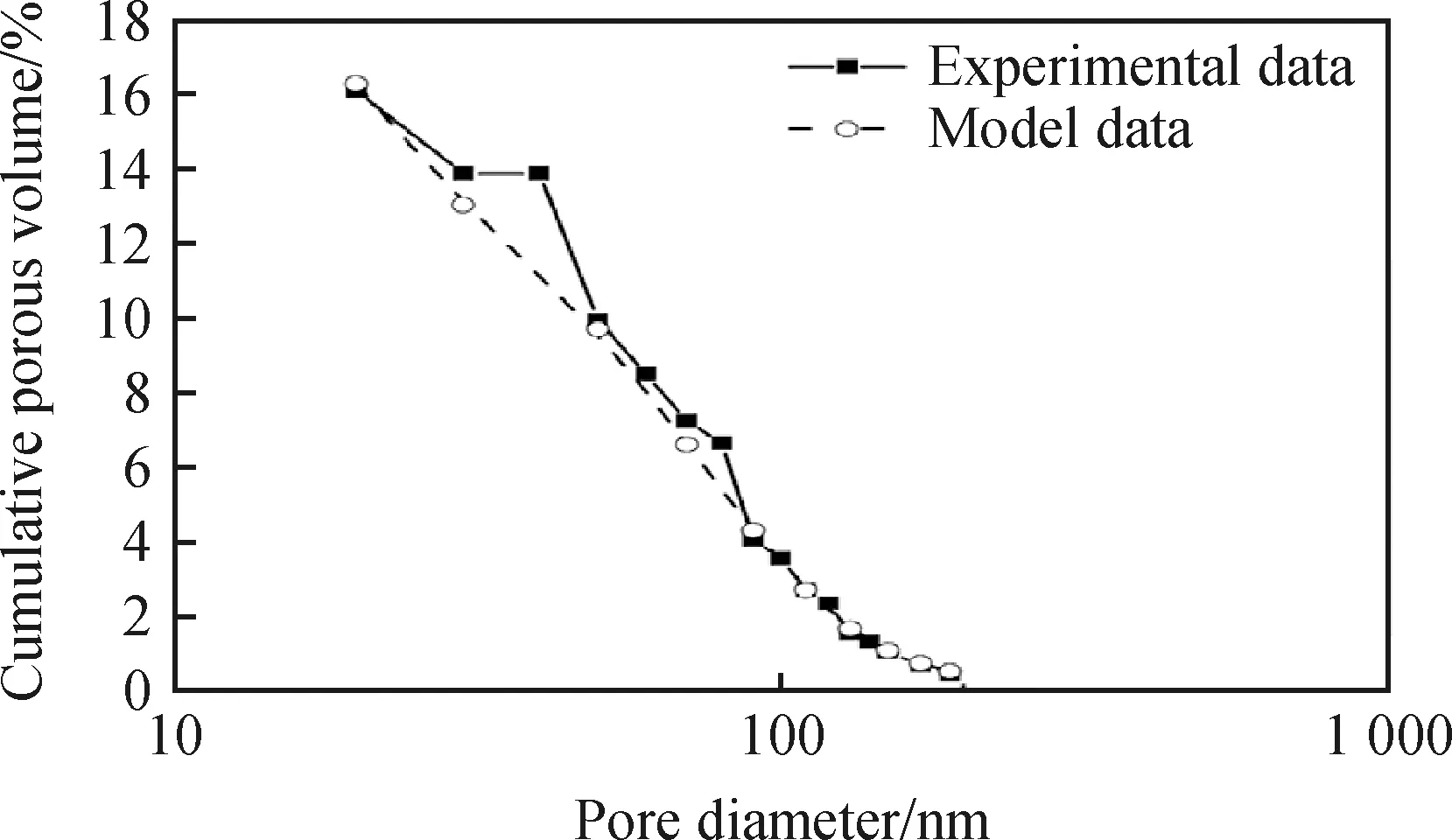
图10 生成的水泥浆模型的累积孔径分布与试验数据对比Fig.10 Comparison of cumulative pore size distribution between the generated cement paste model and the experimental data

从FIB/SEM图像中取出某一5 000 nm×5 000 nm的正方形单元，并与模型中截取的尺寸为3 000 nm×3 000 nm某二维截面进行比较，如图11所示。模型的孔隙网络形态、分布有很强的随机性，这是由随机场的特性所决定的，但单从模型孔隙尺寸与密度来看，与FIB/SEM的结果有很大程度的相似性。由于本方法是将三维随机场二相化以后联合构成模型，如果从模型中任意取一个二维截面来看，不同截面内的孔隙尺寸分布相差较大，有的二维截面截取到较少大孔隙的断面，则会出现大孔隙，有的二维截面没有截取到较少大孔隙的断面，则以小孔隙为主，因此，二维截面内的孔径分布无法与试验孔径分布曲线对应，但整体三维孔隙的尺寸经过以八面体为结构单元的形态学验算后满足试验孔径分布。此外，由于该方法将孔隙网络形态和分布随机化，基于与试验孔隙分布曲线反演进行建模，故无法呈现出材料孔隙的一些天然特征以及天然微裂隙等，会一定程度影响模型与真实孔隙网络形态的相似程度。

图11 模型截面与FIB/SEM图像[21]比较Fig.11 Comparison of model cross-section with FIB/SEM image[21]

3 结 论

本文采用高斯随机场偏移集理论和数学形态学图像处理方法完成并验证了W/C=0.64的水泥浆三维孔隙结构模型。与传统的基于简单单元的孔隙介质建模方法相比，该方法在保证模型孔隙率与真实值相符的前提下，对孔径分布有着较好的控制，且能够呈现出孔隙网络三维形态和空间分布的随机性。更细的网格划分或更多的不同相关长度的二相场的联合可以使模型的孔径分布更准确地满足试验孔径分布曲线，但也会带来更长的计算时间。此方法同样适用于其他类型的不考虑材料中天然缺陷的孔隙介质的建模，且基于此模型可以进一步开展力学和渗流特性研究。