Cox比例风险模型的弹性SCAD变量选择方法及应用*

孙志华，谢向东，焦东方

(1.中国海洋大学数学科学学院，山东 青岛 266100；2.东北师范大学数学与统计学院，吉林 长春 130024)

变量选择问题是统计领域中的研究方向之一。基于惩罚思想的变量选择方法(也称正则化回归方法)，在选出变量的同时也对变量参数作出了估计，其计算量相对较小，相比其他变量选择方法呈现出诸多优越性。这使得，以Lasso为代表的基于惩罚的变量选择方法得到广泛研究，出现了一系列基于惩罚的变量选择方法：Bridge、Lasso、SCAD、Elastic Net、Adaptive Lasso、Dantzig Selector、MCP等。虽然Lasso具有较好的预测结果，但一般情况下Lasso结果是有偏的，在严格的条件假设下才具有相合性，并且Lasso不具有oracle性质[1]。而SCAD、Adaptive Lasso、Dantzig Selector以及MCP具有oracle性质。West等[2]提出当“large p, small n”时，要特别重视成组变量(Grouped variables)的问题。针对此类问题，Hastie等[3]、Díaz-Uriarte[4]提出了主成分分析法，Hastie等[5]提出了监督tree harvesting方法，Dettling和Bühlmann[6]将聚类和有监督学习结合在了一起，Segal等[7]论证了正则化回归方法处理成组变量的优势，Zou和Hastie[8]提出了变量选择方法的组效应(Grouping effect)。Lasso处理成组变量的效果非常差，而SCAD、Elastic Net、Adaptive Lasso、Dantizig Selector、MCP中，仅Elastic Net方法具有组效应。

由于生存数据的删失性，完全数据的变量选择方法不能直接应用于生存数据，因而一些学者研究了Cox比例风险模型(简称之为Cox模型)的变量选择问题：Tibshirani[9]、Fan和Li[10]分别将Lasso、SCAD应用于Cox模型，Li和Luan[11]提出了Cox核转换方法，Zhang和Lu[12], Zou[13]将Adaptive Lasso应用到Cox模型，闫丽娜[14]将Elastic Net与Cox模型结合，侯文[15]研究了Cox模型的桥估计(Bridge)，邓秋玲[16]研究了SCAD和Adaptive Dantizig Selector在Cox模型中的应用，刘丹等[17]研究了Adaptive Elastic Net在Cox模型中的应用。

为了使高维生存数据的Cox模型的变量选择方法既有oracle性质，又具有组效应，本文提出了Cox模型的弹性SCAD方法，并证明了弹性SCAD方法的统计性质，通过数值模拟，比较了在Cox模型下，弹性SCAD与Lasso、Adaptive Lasso、SCAD、Elastic Net、Adaptive Elastic Net等方法的变量选择结果，得到了弹性SCAD在某些情况下的优越性，最后再结合实例，探讨了弹性SCAD及其他变量选择方法应用于Cox模型处理生存数据的表现优劣。

1 基于Cox模型的弹性SCAD方法及性质

首先，我们给出Cox模型的弹性SCAD方法的估计：

(1)

R(ti)表示ti时刻的危险集，δi是表示是否删失的示性函数。γ>2,λ1>0,λ2>0为调整参数

xi=(xi1，xi2，…，xip)，表示矩阵X的第i行。

故

(2)

(3)

记Q(β)=-ln(β)+Pλ1,λ2(β)。

(4)

我们可以得出基于Cox比例风险模型的弹性SCAD方法有以下性质(证明见附录)：

a=max{|xij-xiτ|},i∈{1,2,…,n},j,τ∈{1,2,…,p}。

性质3(估计一致性) 若n→+,则存在Q(β)的一个局部最优解满足其中

性质4(Oracle性质) 若n→,,则满足

性质5(方差估计的渐近性)

性质1～5的证明见附录。

2 数值模拟

弹性SCAD方法可以看作是SCAD方法和岭回归的结合，具有Oracle性质，其克服了Elastic Net有偏估计的缺点，属于渐近无偏估计。与SCAD相比，具有组效应，且与同样具有组效应的Elastic Net(ENet)、Adaptive elastic net(AENet)相比，其在处理小样本高维数据、变量间存在高度共线性问题与小样本低维、变量间存在弱相关关系两种情况下表现更优。

本部分数据模拟选用十折交叉验证，研究的目的是通过运用基于Cox模型的Lasso、Adaptive lasso(Alasso)、ENet、AENet、SCAD、弹性SCAD(Escad)6种变量选择方法，对模拟生成的高维、并具有不同共线性强弱的生存数据进行变量选择，比较其变量筛选效果以及模型误差等指标，进而评价各种方法的优劣。

数值模拟的参数设置情况如下：设样本量为n,协变量个数为p，生成n×p的数据矩阵X，除前2列外，其余各列服从标准的多元正态分布，第一列数据服从一元标准正态分布，第二列数据与第一列数据之间的相关系数分别设为r(v1,v2)=0.8、0.5和0.2，分别代表变量和间存在强共线性、中等共线性和弱共线性的情况。参数设置为:

v=(v1,v2,v3,…,vp)=(0.8,0.7,1,-0.6,0,0,…,0)。

当变量v1与v2间存在共线性且为重要变量时，若所用变量选择方法同时将v1、v2选进模型，则说明该方法具有变量选择的组效应，否则，说明其没有变量选择的组效应。生存时间删失率设为0.3。

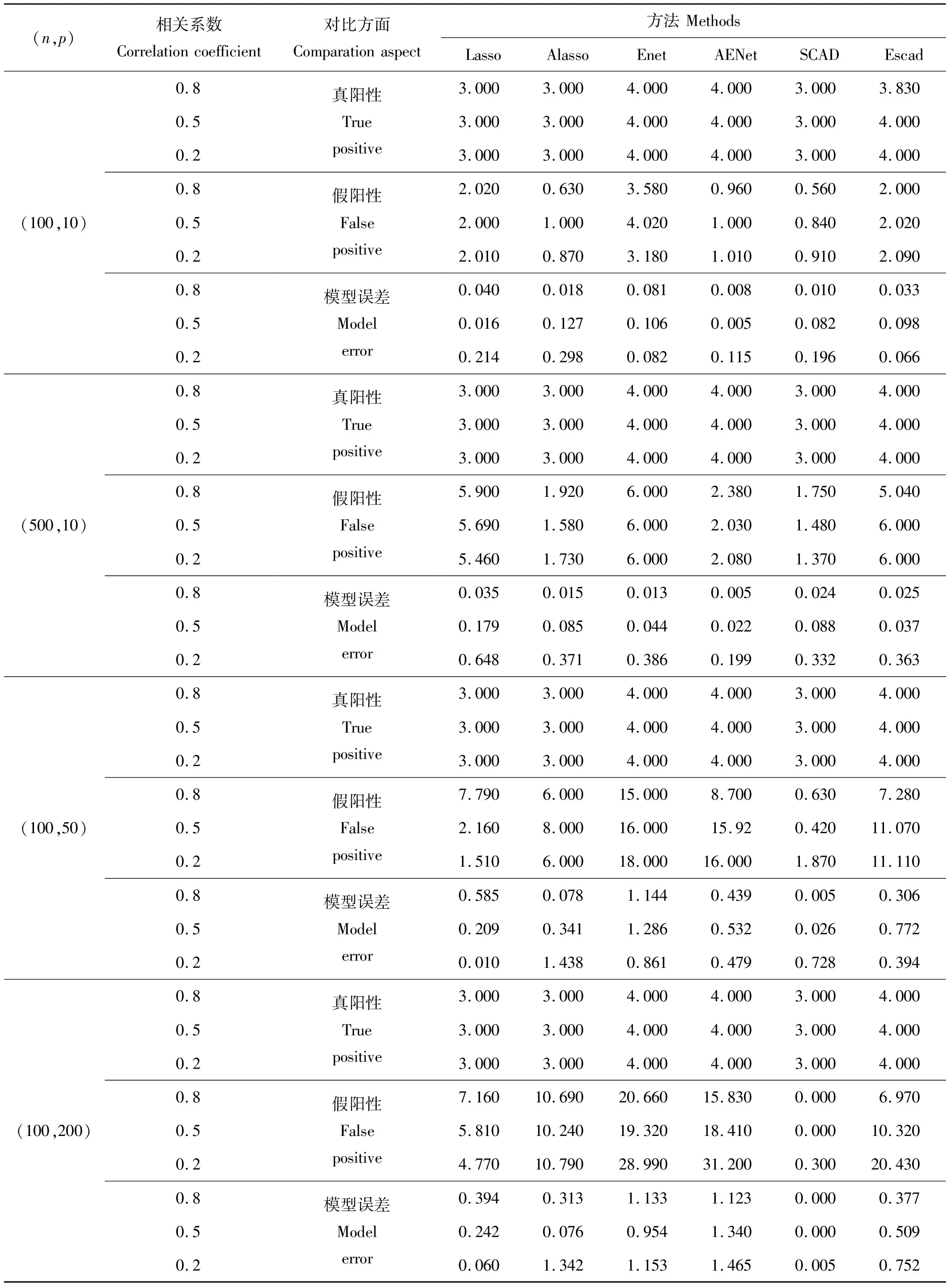
表1 部分数值模拟结果

从图1可以看出，SCAD相比于Lasso、Alasso，其模型误差较小，模型稳定性强；弹性SCAD相比于Enet、AENet，由于其具有Oracle性质，故模型误差较小，模型稳定性强，虽然AENet也具有Oracle性质，但模型表现不如Escad稳定。

图1 6种方法在模型误差方面的表现(相关系数为0.8)

图2给出了当n=100,p=10且相关系数为0.8时，弹性SCAD与SCAD的求解路径的比较，其中图2(a)为弹性SCAD，图2(b)为SCAD。

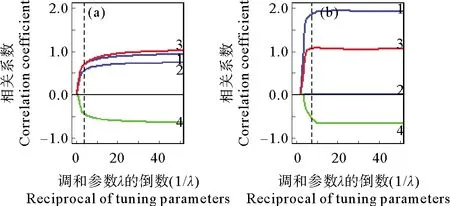
(n=100,p=10,r(v1,v2)=0.8。曲线1～4分别为v1～v4的估计值。n=100, p=10, r(v1,v2)=0.8.line 1～4 are the estimators of variables v1～v4.)

结合图1和2可以看出，弹性SCAD在保留了SCAD变量选择优点的同时，克服了SCAD方法在进行变量选择时不具有组效应的缺点，在变量间存在高度相关性时，能够把相关的变量同时选进模型，具有变量选择的组效应。

从数据模拟结果可以看出：不具有变量选择组效应的方法是基于Cox模型的Lasso、Alasso、SCAD；具有变量选择组效应的方法是ENet、AENet、弹性SCAD。其中三者在对于有组效应的变量选择方法，在n=100,p=50,变量间存在强相关关系与n=100,p=10,变量间存在弱相关关系两种情况下，弹性SCAD模型误差最小，系数估计方面也表现最佳；在n=500,p=10情况、变量间存在非强(中等强度及较弱强度)相关关系时，弹性SCAD在系数估计方面表现最佳；在n=100,p=50情况，变量间存在弱相关关系时，弹性SCAD的模型误差最小。基于Cox模型的Lasso和Alasso均倾向于多选变量，而SCAD与二者相比，虽然也存在假阳性，但除小样本低维、变量间存在弱相关性的情况外，其假阳性的个数均小于二者，故变量选择的一致性方面，SCAD优势明显；基于Cox模型的ENet、AENet和弹性SCAD均倾向于多选变量，而弹性SCAD与二者相比，虽然也存在假阳性，但在n=100,p=50情况下假阳性的个数均小于二者，故变量选择的一致性方面，此情况下基于Cox模型的弹性SCAD方法最优。当n=100,p=200时，不具有变量选择组效应的方法是基于Cox模型的Lasso、Alasso、SCAD；具有变量选择组效应的方法仍是基于Cox模型的ENet、AENet、弹性SCAD；在变量间3种不同程度的相关关系情况下，基于Cox模型的弹性SCAD相比于ENet 和AENet方法，均具有较少的噪声系数、较低的模型误差。

3 实例分析

本实例数据来源于Kalbfleish 和Prentice的一组肺癌治疗方案的临床试验数据[18]，这是一个标准的生存分析数据集。我们对这组数据利用前文提到的6种方法进行变量选择，结果见表2。

由于Diagnosis time, age和prior的值均为0，可以判定其对研究对象的生存时间没有影响；结合Escad、Enet、AENet的选择结果，可知small为噪声系数，对结果没有明显影响；若假设变量间存在相关性，结合数值模拟结果可知，在小样本低维数情况下，AENet表现最优，故理论上其选择的非零个数要比SCAD、Lasso、Alasso要多，而结合表2中数据可知，这4种方法选出的非零个数并无明显差异，甚至不具有组效应的Lasso要比AENet选的还多，这说明这些变量间是不具有相关关系。

表2 对肺癌数据进行变量选择的结果

卡式评分(Karnofsky score)表现得分越高，健康状况越好，越能忍受治疗给身体带来的副作用，因而也就有可能接受彻底的治疗，6种方法均将其选出，比较符合实际；肺小细胞癌是肺癌中最凶恶的，坏死典型且呈广泛性，扩散转移快；而与之对应的，鳞状细胞癌(鳞癌)、腺癌、大细胞癌均为非小细胞型肺癌，与小细胞癌相比，它们扩散转移相对较晚。故根据实际，可把鳞状细胞癌、胰癌、大细胞癌看作一组变量，表2中只有Escad、ENet、Lasso 3种方法同时选进了这3种变量，比较符合实际。但Lasso不具有组效应，故其虽然选进了这3种变量，应该是作为噪声变量选入的，系数估计会很差，故与实际相差比较大；而AENet作为在ENet的基础上的一种改进，却没有将这3种因素同时选入模型，可见ENet选入这3种变量是因为此方法会多选变量。综上，可推知影响研究对象生存时间的主要因素有：Treatment、Karnofsky、squamous、adeno和large影响效用系数分别为：0.099、-0.028、-0.683、0.296和-0.334。

即癌症类型是否为非小细胞癌，是决定生存时间的因素。更进一步，其中是否为鳞状细胞癌的指标为主要决定因素。Karnofsky表现得分虽然对生存时间有影响，但是相对来说其影响是次要的，不起决定性作用。再对比文献[12]中研究结果，可知本文上述研究结果与之相符，但治疗指标trt是否为有效影响因素，对比之下难以确定，有待进一步研究。由于在实际应用中，变量间的关系十分复杂，故不会完全与模拟数据中的表现完全一致，经本例的分析结果，可推知基于Cox模型的弹性SCAD在实际处理生存数据时表现优于文中其他变量选择方法。

4 结论与展望

本文主要研究了基于Cox模型的弹性SCAD变量选择方法的理论性质，通过数值模拟比较得出了如下结论：在n=100，p=50情况下，基于Cox模型的Elastic net和Adaptive elastic net方法在变量选择的一致性上的表现不如弹性SCAD方法；对于有组效应的变量选择方法，在n=100，p=50情况，变量间存在强相关关系与小样本低维、变量间存在弱相关关系两种情况下，基于Cox模型的弹性SCAD模型误差最小，系数估计方面也表现最佳；在n=500，p=10情况，变量间存在非强(中等强度及较弱强度)相关关系时，基于Cox模型的弹性SCAD在系数估计方面表现最佳；在n=100，p=50情况、变量间存在弱相关关系时，基于Cox模型的弹性SCAD的模型误差最小。

当n=100，p=200时，在变量间3种不同程度的相关情况下，基于Cox模型的弹性SCAD相比于Elastic net 和Adaptive elastic net方法，均具有较少的噪声系数、较低的模型误差。进一步通过实例分析发现，基于Cox模型的弹性SCAD的变量选择结果优于文中讨论的其余变量选择方法，变量选择结果较为合理，与实际更相符。

通过多种方法的实例比较分析，可以判断变量间是否存在共线性，有利于在决策时选择更适合的方法，作出更理性、正确的判断，进一步可知，通过比较这几种方法在不同类型参数下的表现，可判断共线性的强弱，在实际应用时，提供一个较为理性的方案。

本文只选取了特定删失比例、变量个数、数据个数进行了数值模拟，弹性SCAD与SCAD的模拟程序也不适于处理带有节点的生存数据，且由于设备的局限性，也未能研究弹性SCAD在更高维数据下的表现，结果难免会有一定的片面性。在进一步的研究中，可改进算法、程序、改变删失比例、变量个数及数据个数进行更全面、高效的数值模拟，发现其新的变量选择特性或局限性所在，从而更好地应用于理论研究和实践方面。