深度学习方法在海浪有效波高数据高分辨率处理中的应用*

朱晓雯，侯 宇，刘玉海，吴克俭**

(1.中国海洋大学海洋与大气学院，山东 青岛 266100；2.中国海洋大学数学科学学院，山东 青岛 266100；3.中国科学院海洋研究所，山东 青岛 266100；4.中科曙光国际信息产业有限公司,山东 青岛 266100)

有效波高(Significant Wave Height, SWH)是海浪研究中一项重要的海洋要素。在物理海洋学中，有效波高在传统上被定义为最高三分之一波(H1/3)的平均波高[1]，即前三分之一大波波高。有效波高是重要的海浪要素，也是描述海况主要参量之一，被广泛应用于海洋数值模拟、海岸工程和航海运输等领域。高分辨率的SWH数据能为多尺度物理海洋学研究以及海浪精细化预报、防灾减灾、海气耦合模式的发展等工作提供更加有效的数据支撑。在推动海-气耦合模式的过程中，需要对每个海洋网格增强像素化，这样才能更好地解析中小尺度的气候变化过程，然而随着空间分辨率的提高，所需要的计算量级也急速增长。

随着人工智能技术的迅速发展和显卡(GPU)在加速运算中的广泛使用，深度学习方法被广泛运用于海洋和气象等自然科学研究中[2-8]。Wang等[9]归纳总结了适用于不同类型时空数据的深度学习方法，并分类统计了近年来深度学习方法在气候和天气学中的研究结果。除了传统的插值方法之外，近年来有很多深度学习的方法也被用来解决海洋数据的降尺度问题。降尺度是从低分辨率(Low-Resolution, LR)重建高分辨率(High-Resolution, HR)数据的过程。二维数据的降尺度处理可以对应计算机视觉和模式识别领域中图像的超分辨率问题[10]。基于神经网络的超分辨率算法的基本思想是建立从低分辨率图像到高分辨率图像的一个映射[11]，Aurélien等[12]使用卷积神经网络结构对海表面温度(Sea Surface Temperature, SST)图像进行高分辨率处理，利用深度神经网络解决海洋遥感数据的降尺度问题，取得了优于传统方法的效果。在进行大批量海洋数据的高分辨率处理时，传统的简单插值方法速度快，但精确度稍低(如双三次插值)，复杂一点的插值方法虽能取得较好的差之效果，但是计算复杂，处理速度较慢(如克里金插值)。基于以上事实，作者思考能否改进深度学习的方法，找到一种既能快速计算高分辨率处理效果，又能媲美甚至超越复杂插值方法的方案。

本文运用了多种方法对SWH数据进行处理，包括传统的双三次插值(Bicubic interpolation)、克里金插值(Kriging interpolation)以及改进的深度学习方法：超分辨率卷积神经网络(Super-Resolution CNN，简称SRCNN)，用峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)等多种评价指标比较了各种方法的高分辨率处理效果。

1 数据和方法介绍

1.1 数据来源及预处理

本文的SWH数据来源于欧洲中期天气预报中心(European Center for Medium Range Weather Forecasting, ECMWF)发布的ERA Interim, Daily数据集，与之前发布的ERA-15和ERA-40产品相比，该数据集使用了最新的四维变分同化技术，其中海浪数据运用耦合海浪模式数据和大量的卫星数据、浮标观测数据进行同化[13]。选取东太平洋海区的有效波高数据，空间范围为:109.625°W～132°W, 0°～22.375°S，空间分辨率为0.125°×0.125°，时间范围从2011年1月1—31日，时间分辨率6 h，即每天四个时刻数据(0时、6时、12时、18时)，共124个时刻的SWH场，数据大小为180×180。

Dee等[14]指出，在模式开发和数据同化方面，ECMWF数据具有良好的效果，而且从多个角度验证了ERA-Interim数据集的优越性。Mooney等[15]在爱尔兰冬季气温的模拟结果中发现，运用ERA-Interim数据模拟的结果更符合实际的观测气温，两者相关性系数更高，而且比使用ERA-40和NNRP-1数据模拟的结果稍好。以上事实有力证明了本文所选数据的可靠性，基于这些数据的结果也是科学可信的。

将高分辨率数据处理成缩小六倍的低分辨率数据用于测试，数据大小变为30×30，空间分辨率从0.125°×0.125°降为0.75°×0.75°。每种方法展示了两次实验测试，测试数据选择标准是：在测试集中选择形态分布差异较大的两个时刻，以保证模型对于处理不同分布状态的低分辨率海浪数据具有普适性效果。

1.2 评价指标介绍

1.2.1 RMSE和PSNR 均方根误差(Root-Mean-Square Error，RMSE)是一种常用的测量数值之间差异的量度，是估计量与真实量之差期望值的平方根，对于两个m×n的矩阵I1和I2，它们的RMSE定义如式(1)，本文中RMSE单位为米(m)。

(1)

峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)经常用作图像处理等领域中信号重建质量的测量方法，是一种评价图像质量的客观标准。通常图像经过处理后，在某种程度上输出的图像会与原始图像有所差别。为了衡量经过处理后的图像质量，使用PSNR作为评价图像质量的指标，判断图像处理程序结果是否令人满意。PSNR通过均方误差(Mean Square Error，MSE)进行定义，对于两张m×n的灰度图像I1和I2，它们的均方误差(MSE)定义如式(2)：

(2)

峰值信噪比PSNR定义如式(3)：

(3)

其中：MAXI表示图像像素点颜色的最大数值，对于灰度图像，图像每个采样点用8位表示，则MAXI=255。为了统一比较标准，在计算PSNR时使用标准化到0～255范围的SWH数据。

1.2.2 SSIM 结构相似度(Structural Similarity,简称SSIM)[16]被用来测量两个图像之间的相似性。SSIM的设计是为了改进传统的图像评价方法，如峰值信噪比(PSNR)和均方误差(MSE)。结构相似性的基本思想假定自然影像是高度结构化的[17]，即在自然影像中相邻像素之间有很强的关联性，而海浪有效波高数据也具有这种关联性，而这样的关联性承载了海洋要素的结构信息。相较于传统图像衡量指标(如PSNR)，结构相似性(SSIM)在图像品质的衡量上更能符合人眼对图像品质的判断。

给定两张图像x和y，两者的结构相似性定义如公式(4)所示：

(4)

式中：l(x,y)是亮度项；c(x,y)是对比度项，s(x,y)是结构项；α>0,β>0,γ>0，这三项是调整l(x,y)、c(x,y)、s(x,y)相对重要性的参数；μx及μy、σx及σy分别为x和y中像素点的平均值和标准差，σxy为x和y的协方差；C1,C2,C3都为常数，用来保持l(x,y)、c(x,y)、s(x,y)的稳定。结构相似性指标的值越大，代表两张图像相似度越高。本文在具体计算时，令α=β=λ=1及C3=C2/2，得到式(5)：

(5)

计算SSIM时同样使用标准化到0～255范围的SWH数据。

1.2.3 余弦相似性(Cosine similarity) 对于两个图像(或矩阵)A和B，其余弦相似性(Cosine similarity)由点积和向量长度给出，如式(6)所示，式中Aij和Bij分别代表A和B对应点的值。

对于图像来说，像素值都为非负值，余弦相似性的范围从0到1，1表示两张图像是完全相同的，0通常表示它们之间是独立的，而在这之间的值则表示中间的相似性或相异性。为了统一比较标准，在计算余弦相似度时用标准化到0～255范围的SWH数据。

(6)

1.3 方法介绍

1.3.1 双三次插值 在数学上，双三次插值(Bicubic Interpolation)是常用的二维数据的插值方法。插值后得到的曲面比双线性插值或最近邻插值方法得到的相应曲面更加光滑。双三次插值可以使用拉格朗日多项式、三次样条或三次卷积算法。在本文中使用由Keys[18]提出的三次卷积算法。

本文中将30×30的低分辨率数据用双三次插值的方法高分辨率处理为180×180的规格，即分辨率提高了六倍，分辨率从0.75°×0.75°变为0.125°×0.125°。

1.3.2 Kriging 在最初在地质统计学中，克里金法(Kriging)或称高斯过程回归法(Gaussian process regression)是一种插值方法，插值后的值由先验协方差控制的高斯过程建模得出。在适当的先验假设下，克里金法给出了对中间值的最佳线性无偏估计[19]。该方法广泛应用于空间分析和计算机实验领域。Jessica等[20]运用Kriging方法确定鲸类动物保护的潜在区域；Lin等[21]将普通克里金法应用于气温和光合有效辐射量等气候要素的插值。本文运用了普通的克里金方法(Ordinary kriging)进行计算。

同双三次插值方法(Bicubic interpolation)一样，将30×30的低分辨率数据用Kriging方法高分辨率处理为180×180的规格，分辨率从0.75°×0.75°变为0.125°×0.125°。

1.3.3 SRCNN 超分辨率卷积神经网络(Super-Resolution CNN，简称SRCNN)是由Dong等[22]提出的解决超分辨问题的深度学习方法，计算过程如图1所示。对于给定的低分辨率图像Y, SRCNN的第一卷积层提取一组特征图，第二层将这些特征映射到高分辨率的特征图上，最后一层结合空间邻域内的预测，生成最终的高分辨率图像F(Y)[22]。该方法的实质是运用卷积神经网络(Convolutional Neural Network，CNN)直接学习低、高分辨率图像之间的映射。本次研究中，低分辨率的数据是先由高分辨率数据进行切割，得到33×33的高分辨率切片，再将切片进行六倍下采样，然后对缩小的切片用临近插值法处理得到与高分辨率数据尺寸相同的，但“模糊”的低分辨率数据。这样就得到了许多一一对应的低、高分辨率数据，建模学习这些低、高分辨率数据的映射关系。

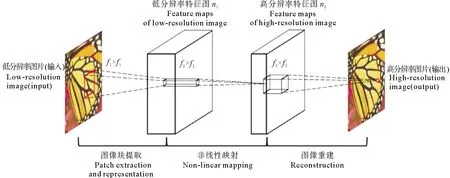
图1 SRCNN过程展示

运用SRCNN方法时，我们需要划分训练集和测试集，为了避免临近时间造成训练集和测试集的高度相似，本文选取前100个时刻的高分辨率数据作为训练集，剩余的数据用作测试。

传统的SRCNN超分辨率方法用于处理图像，即数据类型为整型，范围在0～255之间，而这并不能完全满足实际海洋问题的应用。Aurélien等[12]解决了SST图像数据的高分辨率问题，但并没有将其结果转化为真实的SST数据，因此也无法为进一步的海洋要素分析提供真实数据，且由于图像数据均为整数，即使转化为真实海洋数据，数据取值范围也仅有256个值，数据精度有限，这就大大降低了深度学习方法的实用性。为了解决该问题，并且与传统的SRCNN方法作比较，本文设计了两种实验方案(SRCNN的方案一和方案二，分别用SRCNN_1、SRCNN_2表示，下同)：

SRCNN_1：将SWH数据标准化到0～255范围，存为三通道灰度图，此时数据均为图片格式，数据类型为整数型，用搭建好的SRCNN架构训练一个六倍超分辨率重建的模型，此模型的输入输出格式均为图片格式，想要得到真实的SWH数据，需要逆标准化的过程，将0～255范围的图片数据转化为真实SWH数据。

SRCNN_2：对传统的SRCNN框架进行改进，在模型的数据读取部分和数据预处理部分进行改进，使模型能做到大批量读取真实SWH数据，并在模型内部进行标准化过程。重新训练浮点数矩阵数据的超分辨率模型，训练好的模型可以实现输入低分辨率SWH数据，输出高分辨率SWH数据，无需额外进行数据类型的转化，使用效果更加便捷，处理数据效率更快。

将两种方案分别在服务器上进行训练，除了训练集的数据类型不同外，其他参数均相同，网络结构的参数设置如表1所示。

表1 SRCNN网络结构

SRCNN方法使用搭建在LINUX服务器上的TensorFlow框架进行计算。TensorFlow是谷歌大脑(Google Brain)团队开发的第二代机器学习系统[23]。该方法用两块型号为NVIDIA GeForce GTX 1080Ti的显卡进行计算，极大提高了计算速度。具体参数的设置见表2。

表2 SRCNN方法参数设置

3 高分辨率处理效果

对于每种方法，本文选择了两个SWH分布差异较大的时刻进行实验，分别为2011年1月29日18时和31日6时的SWH场。图2和3分别展示了两次实验的低分辨率、高分辨率SWH场和各种方法的处理效果。

与原始高分辨率SWH相比，四种方法的高分辨率处理效果在空间分布趋势方面均没有很大的出入。因此在分析SWH分布这种定性问题时，双三次插值、Kriging插值和SRCNN两个方案的结果均能满足要求。

从细节分析，SRCNN_1的结果如图2(e)、3(e)所示，具有明显的片状结构，SWH场分布连续性不如其他的方法。这是因为该方法使用的训练集是图像格式，转化真实的SWH数据时，数值范围为0～255的整数，而SRCNN_2的设计很好地解决了这一问题，数据连续性有了明显提高，更加适合处理SWH的高分辨率问题。

((a)低分辨率SWH；(b)原始高分辨率SWH；(c)双三次插值；(d)kriging插值；(e)SRCNN_1；(f)SRCNN_2。(a)Low resolution SWH；(b)Original high resolution SWH；(c)Bicubic interpolation；(d)Kriging interpolation；(e)SRCNN_1；(f)SRCNN_2.)

((a)低分辨率SWH；(b)原始高分辨率SWH；(c)双三次插值；(d)kriging插值；(e)SRCNN_1;(f)SRCNN_2。(a)Low resolution SWH；(b)Original high resolution SWH；(c)Bicubic interpolation(d)Kriging interpolation；(e)SRCNN_1;(f)SRCNN_2.)

4 分析与讨论

4.1 指标分析

分别计算四种方法所得结果的评价指标(SSIM，PSNR，RMSE，COSINE)(见表3)。四种方法的SSIM 和COSINE 两项指标相差不大，结果都很接近1，说明从视觉上来看，四种方法的插值效果与原始高分辨率的数据非常相似，在定性分析SWH分布特征时均能满足要求。从PSNR指标来看，Kriging方法最优，其次是SRCNN_2和SRCNN_1，而这三种方法与Bicubic方法相比，在PSNR上有了较大幅度的提高。RMSE指标方面，Kriging和SRCNN_2最优，明显优于其他两种算法，说明Kriging和SRCNN_2方法的整体误差比较小，误差范围在±0.01 m左右。但是由于Kriging方法对于不同时刻的数据都要重新进行大量计算，因此处理大批量数据时面临计算效率低、计算量大的问题。而SRCNN的方法在训练好一个区域的模型之后，可以快速、大量地处理该区域不同状态的SWH数据，每次处理过程仅仅是多层矩阵运算，大大提高了计算效率，具有快速、大批量处理数据的能力。

表3 海表面有效波高场高分辨率处理效果的不同指标

从各项指标结果上看，Kriging算法与两种SRCNN算法都可以得到很好的高分辨率结果，且明显优于传统的Bicubic算法。而SRCNN_2的各个指标都要优于SRCNN_1，表明本文对于SRCNN方法的改造有明显的提升效果。SRCNN_2在与Kriging方法效果相当的前提下，大大缩短了计算时间和计算量，处理大量的低分辨率数据时，深度学习的方法具有更高的计算效率。

4.2 误差分布分析

本文计算了每一点的估计误差，并求得各种方法所造成误差的最大、最小值(见表4)。分析表中数据可得，在最大、最小估计误差方面，Bicubic算法、Kriging算法和SRCNN_1效果相近，SRCNN_2效果优于这三种算法，不容易出现很大的偏差。虽然上文的结果显示Kriging整体均方根误差比较小，但其在某些点的处理效果不佳，会造成较大的误差。SRCNN_2相比SRCNN_1有了进一步的优化，与其他三种方法相比，SRCNN_2的结果在极端海浪状况的分析问题上更具有优势。

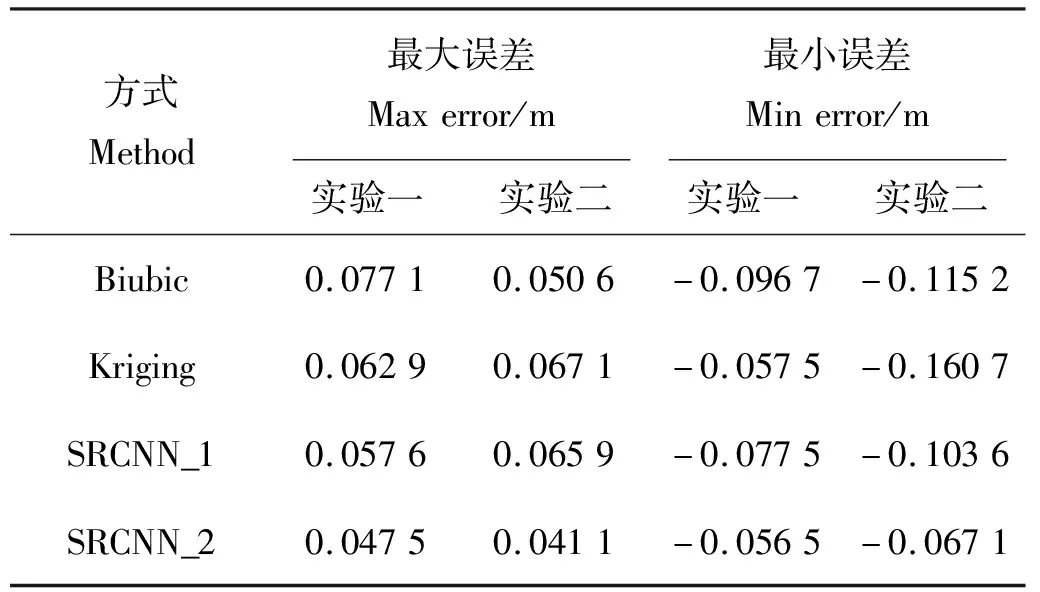
表4 海表面有效波高场高分辨率处理误差的最大、最小值

进一步分析误差的空间分布规律，图4和5分别展示了两次实验的估计误差分布场，分析误差分布特点可以看出：Kriging方法的整体估计(见图5(b))偏高在边缘处的估计偏低且误差大，两种SRCNN算法的误差分布场整体趋势与Bicubic算法一致，但误差范围明显小于Bicubic算法，SRCNN_2比SRCNN_1的误差分布更加均匀，Bicubic、SRCNN_1和 SRCNN_2这三种方法的误差场分布与原始海浪SWH场的分布有关。

((a)双三次插值；(b)kriging插值；(c)SRCNN方案一；(d)SRCNN方案二。(a)Bicubic interpolation；(b)Kriging interpolation；(c)SRCNN_1；(d)SRCNN_2.)

((a)双三次插值；(b)kriging插值；(c)SRCNN_1；(d)SRCNN_2。(a)bicubic interpolation；(b)Kriging interpolation；(c)SRCNN_1；(d)SRCNN_2.)

4.3 近岸海域的测试

为了进一步测试SRCNN_2方法的效果，选取0.75°S～23.125°S，66.875°W～89.25°W的近岸海域进行测试，测试效果如图6所示。相比于双三次插值，SRCNN_2方法在海岸线的还原上效果较好，但是靠近海岸线部分的值偏小。误差原因可能如下：在卷积过程中，对陆地的处理是将其设置为0值，因此在海陆过渡处的插值偏小；训练集中的数据均不包含近岸处的浪场，没有很好地将近岸的高、低分辨率数据的映射关系学到网络中。在今后的实验中，在训练集中加入近岸的数据，会得到较好的改善。

((a)低分辨率SWH；(b)原始高分辨率SWH；(c)双三次插值；(d)SRCNN_2。(a)Low resolution SWH；(b)Original high；resolution SWH；(c)Double cubic interpolation；(d)SRCNN_2.)

4.4 总结与展望

总结以上研究得出结论：整体指标排名：Kriging>SRCNN_2>SRCNN_1>Bicubic,计算效率排名：SRCNN_2>SRCNN_1>Bicubic> Kriging，误差极值效果排名：SRCNN_2>SRCNN_1>Bicubic> Kriging。

综上所述，改进的SRCNN方法(SRCNN_2)是一种在整体效果、局部细节和计算效率方面均比较优秀的高分辨率处理方法，运用显卡进行并行运算大大节约了计算时间，实现了用深度学习方法直接处理原始海浪数据，提高了深度学习方法在海洋数据处理中的实际应用价值。相比于传统的Bicubic和Kriging方法，SRCNN_2的结果为SWH定性分析、定量分析和异常情况分析等提供了更加可靠的数据支持。

在之后的研究中，作者将使用不同的神经网络模型进行高分辨率处理，扩大研究的空间范围和时间范围，讨论不同方法误差分布的规律及产生原因，增加测试量，在地形复杂的近岸海域区域进行计算和实验，进一步提高结果的说服力。