基于迭代启发网络算法的非平稳随机噪声压制

张文征 唐 杰* 刘英昌 孟 涛 陈学国

（①中国石油大学（华东）地球科学与技术学院，山东青岛266850；②中国石化胜利油田勘探开发研究院，山东东营257015）

0 引言

实际地震数据由于采集仪器或者环境等因素的影响，往往存在非平稳随机噪声［1］，在地震数据中以脉冲形式出现，具有较强的能量，主要包括猝发脉冲、异常扰动、声波干扰等［2］，很难用人工方法完全剔除野值和串状干扰［3］。如果中、深层地震资料中存在强能量干扰，则叠前时间偏移剖面会出现不同程度的“画弧”现象［4］。现代地震资料处理的目标是既能衰减噪声、提高地震资料的信噪比，又能保留和增强有效不连续地震反射信息及储层流体信息［5］。常规滤波方法常常放大了噪声的影响，同时噪声的存在也限制了分辨率的提升［6］，并“平滑”了地震数据中的不连续信息。通过自动识别地震记录中的强能量干扰，确定噪声出现的空间位置，根据定义的阈值和衰减系数用适当的方式压制非平稳随机噪声［7］。在动校正后或同相轴相对平直的地震剖面上，中值滤波器具有压制强能量干扰的能力［8-9］，但很难选取合适的阈值算子兼顾保护有效信号和压制噪声［10］。由于异常噪声既不连续也不相关，采用局部中值简单地代替噪声位置处的数据，容易压制有效信号，尤其在同相轴弯曲和间断处［11］。为此，Boashash等［12］提出了一种瞬时频率估计算法——时频峰值滤波算法，基于时频分析理论压制非平稳随机噪声，将含噪信号调制为解析信号的瞬时频率信号，然后取解析信号时频分布的峰值估计有效信号，经时频峰值滤波后信号得到增强，噪声被压制。林红波等［13］提出了基于绝对级差统计量（ROAD）的径向时频峰值滤波非平稳随机噪声压制方法，结合局部时频峰值滤波和径向时频峰值滤波压制地震非平稳随机噪声。

近年来机器学习算法发展迅速，深度学习算法在数据去噪领域的应用也越来越广泛。Burger等［14］推出了具有三层网络的多层感知机模型（MLP），虽然网络结构不深，但是处理效果较好。Schmidt等［15］、Chen等［16］分别提出联合收缩方法（CSF）、反应扩散模型（TNRD），这两种方法的信噪比提高和边缘保护效果超过了块匹配方法（BM3D）。Mao等［17］利用机器学习算法实现了地震数据处理、属性提取、断层预测等方面的云地震数据分析平台。Zhang 等［18］受迭代收缩阈值算法（ISTA）的启发，提出了一种新的结构化深度网络（Iterative Shrinkage-Thresholding Algorithm Network，ISTA-net），能快速、准确地实现数据的去噪和压缩感知重建。

本文利用深度学习算法中的监督数据驱动算法——迭代 启 发 网 络（Iterative scheme inspired network，IIN）压制非平稳随机噪声［19］，该网络结构简单、紧凑。IIN 由交替方向乘子算法（Alternating Direction of Method of Multipliers，ADMM）的迭代过程推导而来，利用L1范数优化变分模型。在训练阶段，通过增加一个新的辅助变量，将目标函数的极值转化为增广拉格朗日格式，使用L-BFGS算法判别、训练所有网络参数，最终得到最优去噪模型参数。在实验阶段，首先利用模型数据和实际数据建立训练数据库，使用训练阶段得到的去噪模型去噪。实验结果表明，与现有的压制非平稳随机噪声方法相比，文中方法具有明显的优势。

1 基本理论与技术流程

1.1 迭代收缩—阈值启发网络算法

噪声消除的目的是从采集到的含噪数据y中恢复无噪数据。传统压缩感知（Compressive Sensing，CS）方法通过求解以下优化问题恢复无噪数据，其目标函数为［20］

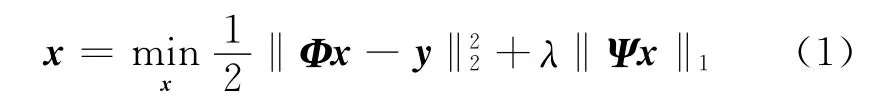
式中：x为无噪数据的估计值；Φ 为变化矩阵，将x变换到不同域；Ψ 为非线性变换函数；λ 为正则化参数。

ISTA-net网络算法结合CS算法，网络由固定的层数组成，每层中一次迭代采用传统ISTA 算法，该网络结合了ISTA 和CS的优势［21］。该网络通过迭代两个更新步骤

估计去噪 数 据［22］。式 中：k 为 迭 代 次 数；s（k）为 步长，根据之前的步长参数由学习确定；T 为软阈值算子的阈值；F（x）为参数可学习的非线性变换函数。

1.2 IIN 算法

非平稳随机噪声主要表现为脉冲噪声，以不规则脉冲或噪声“尖峰”的形式随机出现在地震数据中，持续时间短，具有谱密度较宽和振幅相对较高的特点［23］。由于L2范数对局部异常值的检测不稳定，在压制非平稳随机噪声时会限制算法的处理效果。因此本文采用的IIN 算法在迭代收缩—阈值启发网络算法的基础上，采用L1范数优化噪声压制方程，增强对局部强能量噪声的敏感度［24］，结合ADMM 网络（ADMM-net）［25］，通过优化问题

得到去噪数据。式中l∈［1，2，…，L］为滤波器序号，L 为单层滤波器的总数。滤波器D 的参数由网络进行训练。

引入变量t＝x－y，z＝Dx，则式（3）的增广拉格朗日函数为［26］

式中：ε、ρ为权重系数；α、ω 为拉格朗日乘数矩阵。根据ADMM 算法，引入变量p＝ω／ε，βl＝αl／ρl，则式（4）分解为6个问题

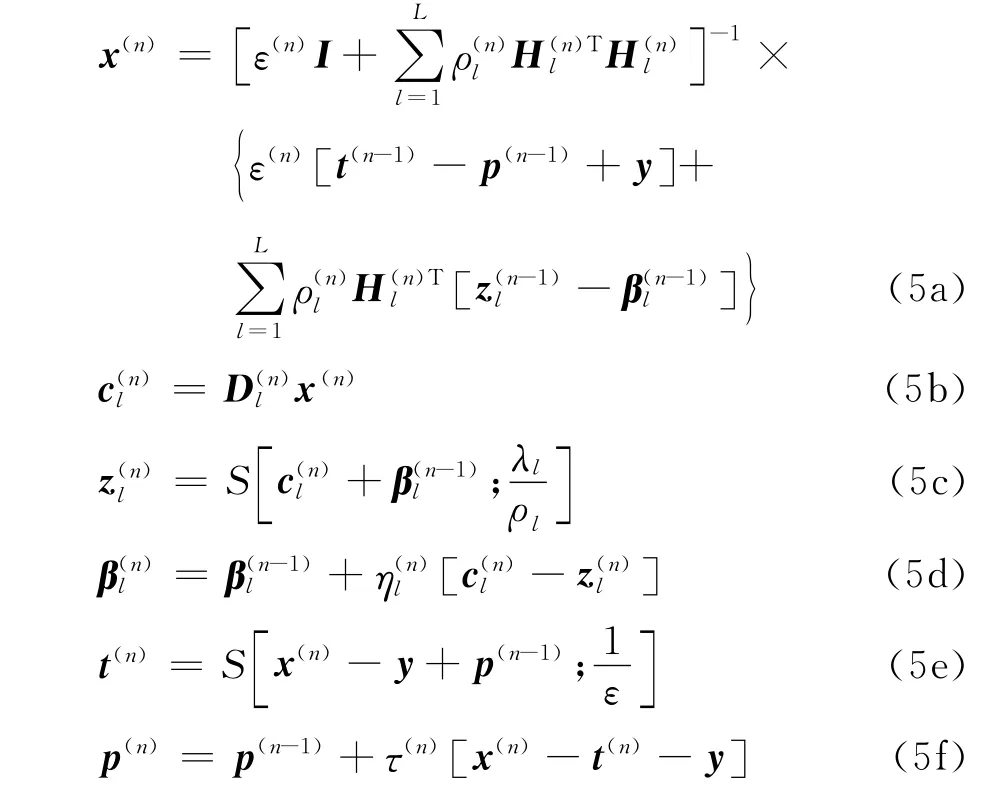
式中：n为层数；S（·）为非线性收缩函数；I为各元素为1的矩阵；Hnl为第n 层中第l 个滤波器矩阵；τ、η为可学习的权重参数，控制学习速率，在网络训练中逐层修正。

1.3 技术流程

在IIN 网络算法中，每层有6个计算节点（对应式（5）），具体步骤如下。

（1）利用式（5a）重构输入的地震数据。若该层是第一层（n＝1）时，式（5a）变为

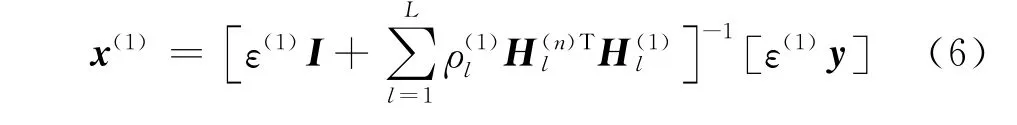
（2）对重构数据x（n）进行滤波处理。

（3）根据式（5c）对滤波数据进行非线性变换，其中S［·］为分段函数，其形式为

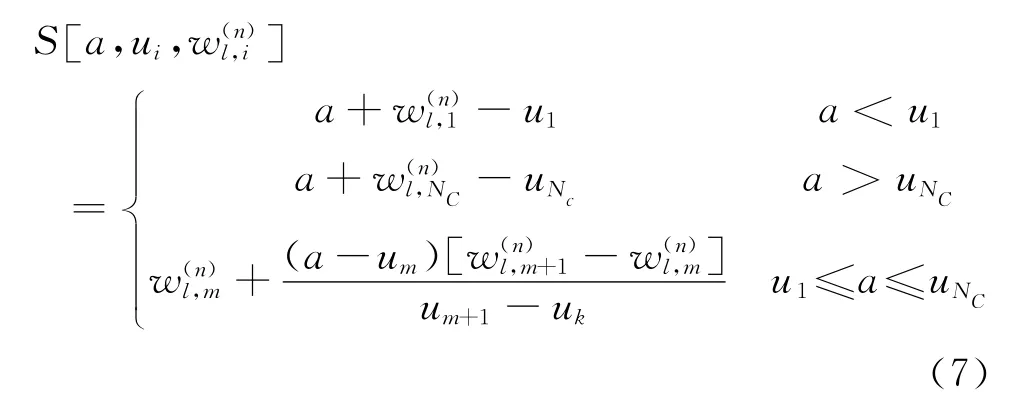
由于分段线性函数拟合性程度高，可以根据数据的特点，学习更加合适的非线性变换函数。其中

（5）对重构数据按步骤（3）进行非线性变换，如果n＝1，即为第1层时，令p（n－1）＝0。

（6）根据式（5f）更新乘数p（n）。

图1为第k层正向传播流程。

在网络训练过程中，通过计算估计数据与输入数据之间的误差作为损失函数

式中Θ 表示上述流程中各个参数的集合。在反向传播过程中计算损失函数E（Θ）对参数集Θ 的梯度，利用L-BFGS算法，通过最小化式（8）的取值，优化去噪数据（y，Θ）的参数集Θ。通过不断循环反向传播过程，使E（Θ）的值不再下降、保持稳定为止，以保证在去噪的同时不压制有效信号。

图2为第k层反向传播流程。通过反向传播计算得到去噪网络参数模型，利用该模型对输入地震数据进行正向传播便可得到去噪后的地震数据。

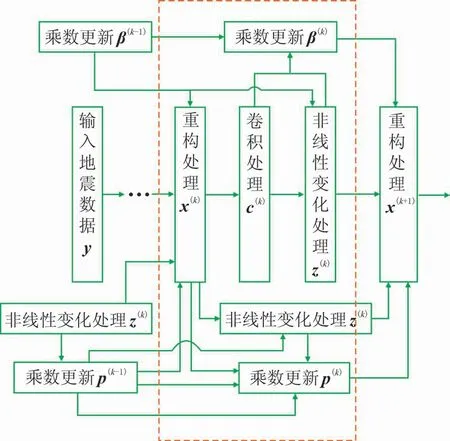
图1 第k层正向传播流程

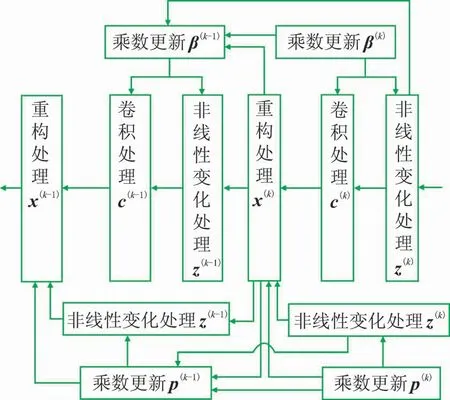
图2 第k层反向传播流程

2 理论模型试算

为了验证上述去噪算法的可行性和有效性，分别对模型数据和实际地震数据进行去噪实验。通过比较不同层数的网络处理效果设置网络总层数，过多的层容易导致过拟合，过少的层数不能有效去除噪声。综合去噪效果和计算时间设置单层滤波器总数目。根据经验设置NC值，关系到分段线性函数的拟合程度。合成地震数据添加了非平稳随机噪声，生成含噪数据作为输入数据，无噪数据作为输出数据；单炮叠前地震数据作为实际数据，存在大量的非平稳随机噪声，采用空变中值滤波和时变中值滤波去噪得到去噪后数据，再选择去噪效果理想的数据作为数据库数据。通过水平翻转和90°旋转将训练数据集扩充，以增加数据的多样性。然后对上述数据训练得到去噪模型。图3 为训练库部分数据。

图4为损失函数曲线与峰值信噪比（PSNR）曲线。由图可见：①在第6次迭代之前，损失函数值呈明显下降趋势，当迭代次数大于6后，损失函数值收敛于小值，说明去噪误差达到最小值，并且其变化趋于平稳，证明训练模型去噪结果稳定（图4a）。②前几次迭代生成的去噪模型的去噪能力不强，经过几次迭代之后，去噪能力趋于稳定，尤其在迭代次数大于7 之后，去噪数据的PSNR 较高且稳定（图4b）。由于采用简单、紧凑的网络结构，因此曲线收敛速度较快，表明文中方法用相对较小的数据集和较少的训练时间得到了稳定的去噪模型。

根据模型中有效信号的能量在合成数据（图5a）加入非平稳随机噪声得到含噪数据（图5b），再利用训练好的网络模型去噪得到去噪结果（图5c）。可见，经过去噪后噪声被压制，去除的噪声（图5d）中基本不存在有效信号，提高了信噪比。为了对比对叠后模型的去噪效果，分别利用本文方法与传统中值滤波方法对含噪模型（图6a）去噪，结果表明：本文方法的去噪结果（图6b）没有残留噪声，去除的噪声（图6c）中不存在有效信号；中值滤波方法的阈值设置影响了去噪结果（图6d），部分有效信号被压制，如果阈值设置太大，则会残留噪声，很难选取合适的阈值有效地压制噪声。

图3 训练库部分数据

图4 损失函数曲线（a）与峰值信噪比（PSNR）曲线（b）

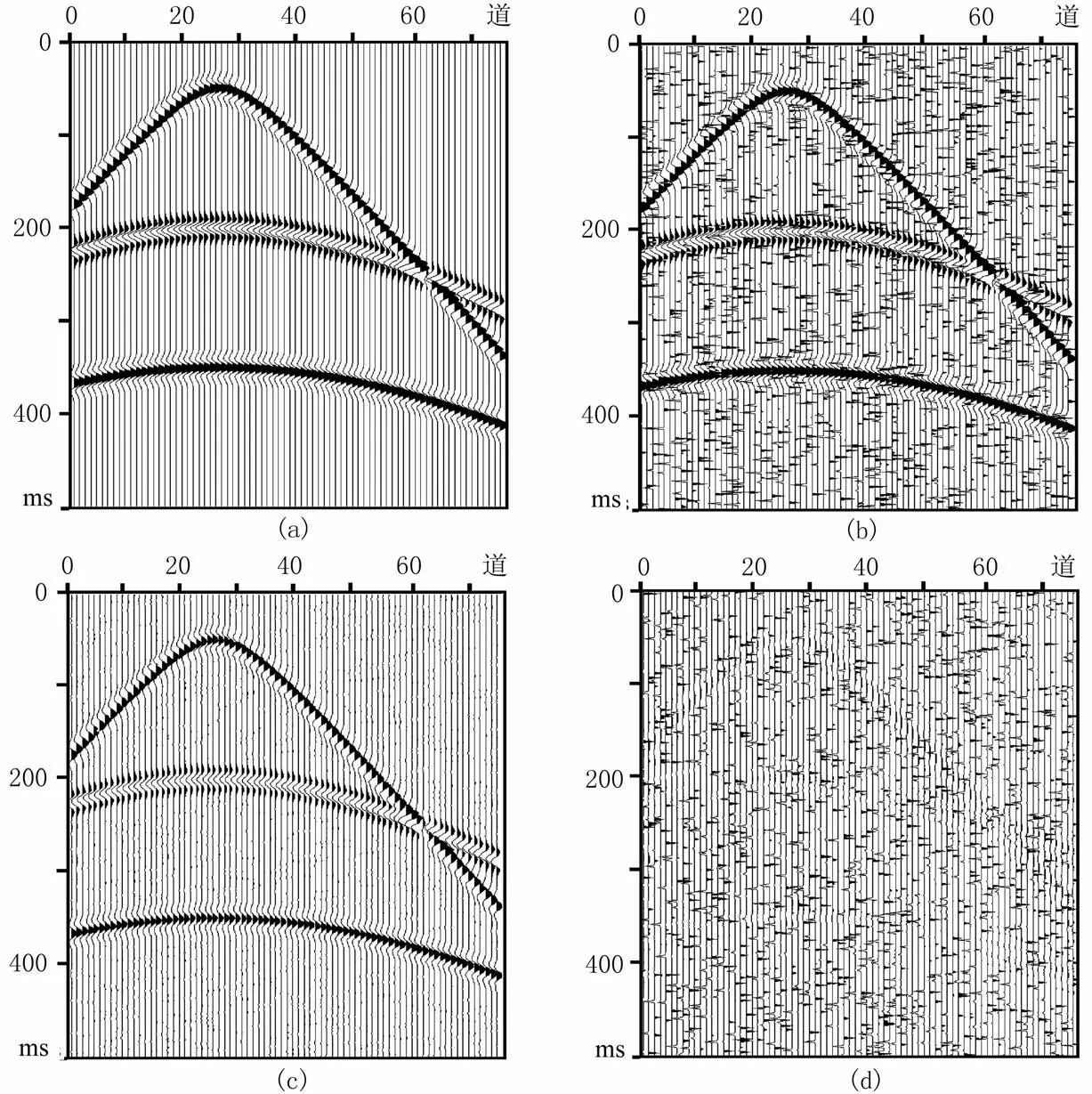
图5 数据模型的去噪效果

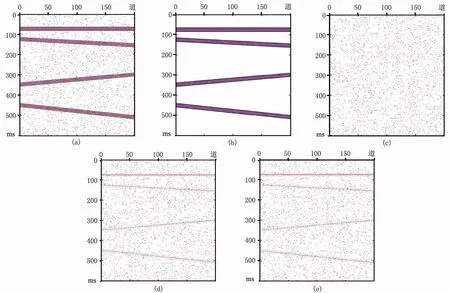
图6 对叠后模型的去噪效果

图7为图6第10道数据去噪前、后对比。由图可见：由于本文方法噪声压制方程的保真项采用L1范数，可更敏感地检测地震数据中的非平稳随机噪声并进行压制（图7a）；中值滤波去噪结果中有效信号也被压制，去噪效果不理想（图7b）。

图7 图6第10道数据去噪前、后对比

3 实际地震数据的应用

分别采用时频峰值滤波方法和本文方法对实际地震数据去噪并分析去噪结果。图8为F 区实际地震数据去噪结果。由图可见：86道实际地震记录中有几道含有较强的非平稳随机噪声，干扰有效信号并影响弱有效信号的拾取（图8a）；时频峰值滤波对图8a的去噪结果中残留噪声（图8b）；经本文方法对图8a去噪后有效压制了噪声，没有破坏有效信号且很好地保护了弱有效信号（图8d）。

单点高密度地震资料信号频带宽、波场信息丰富，反映了地下真实的反射信息，但同时也存在大量的噪声，因此出现信噪比较低、有效信号与噪声混杂的问题，不易发挥高密度资料的潜在优势。为了检验本文方法对单点高密度地震数据的去噪效果，在训练库中增加相应的单点高密度数据，并选取G 区的单点高密度单炮道集进行去噪实验。图9 为G区单点高密度地震数据去噪结果。由图可见：经本文方法对单点高密度地震数据（图9a）去噪后，在压制非平稳随机噪声的同时，保护了有效信号（图9d箭头处）；时频峰值滤波方法对图9a的去噪结果中残留噪声（图9b箭头处）。图10 为图9 的局部放大。由图可见：时频峰值滤波处理结果中残留噪声（图10b）；本文方法去噪结果的同相轴清晰、连续，有效压制了噪声（图10c）。

图8 F区实际地震数据去噪结果

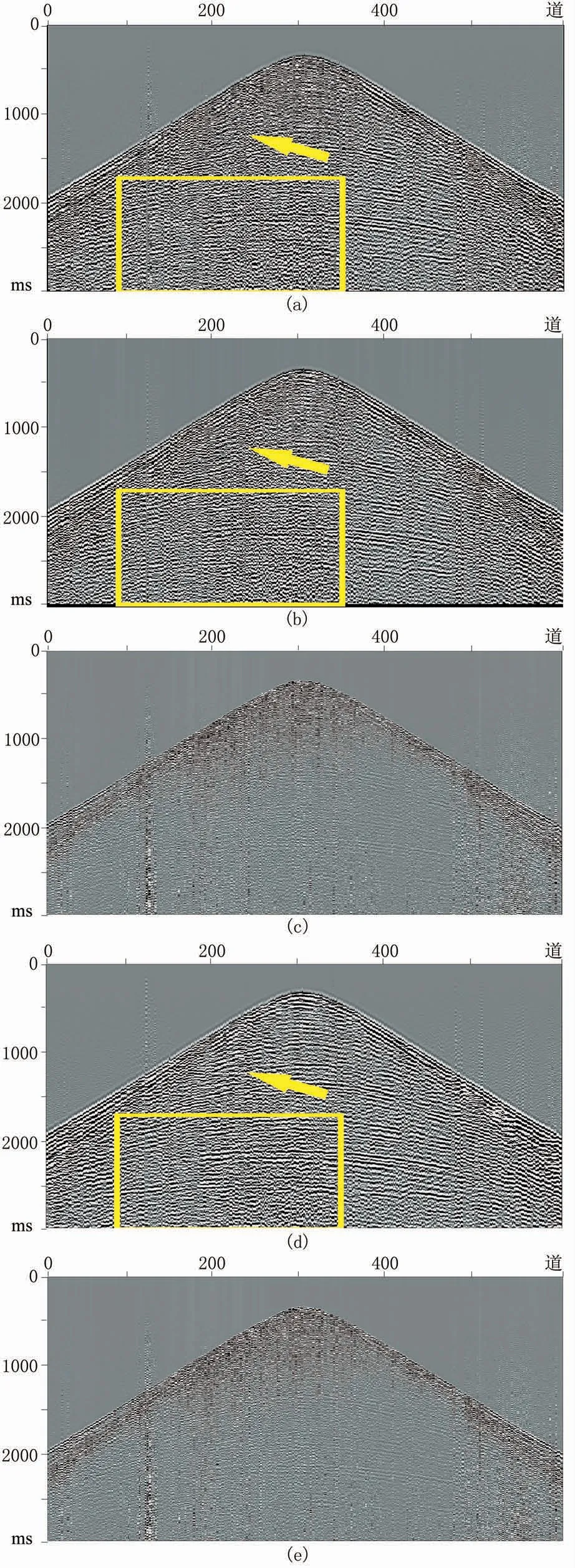
图9 G 区单点高密度地震数据去噪结果

理论模型试算和实际地震数据去噪结果表明，本文方法有效减小了信号畸变，较好地压制了各种非平稳随机干扰，且对实际数据具有较强适应性。

图10 图9的局部放大

4 结束语

针对地震数据中的非平稳随机噪声，本文提出了采用基于迭代启发网络算法的去噪方法，采用深度学习算法，利用L1范数对目标函数进行优化，可更敏感地检测并压制地震数据中的非平稳随机噪声，同时较好地保护有效信号。理论模型及实际资料的去噪结果表明：

（1）利用迭代启发网络（IIN）算法，通过构建包含不同形态有效信号同相轴的数据，并结合实际地震数据建立训练数据库，由训练得到的去噪模型根据有效信号的特征，在去噪的同时可保留同相轴的形状特征；采用的迭代网络简单、紧凑，加快了网络的收敛速度，用相对较小的数据集和较少的训练时间快速训练去噪模型，去噪效果较好。

（2）本文方法具有较强的适应性，有效压制了常规地震数据中的非平稳随机噪声。对于单点高密度地震数据，较传统的时频峰值滤波算法，可有效减小信号畸变，较好地压制各种非平稳随机干扰。