铁磁性材料缺陷的脉冲涡流检测系统设计

任旭虎，张圣坤，张 振

(中国石油大学(华东) 海洋与空间信息学院，青岛 266580)

脉冲涡流(Pulsed Eddy Current，PEC)检测技术作为一种无损检测技术，以电磁感应原理为基础，根据检测所得到电信号的变化来判定检测试件的缺陷位置以及缺陷情况[1-2]。

PEC检测信号频率丰富，信号中所包含的低频涡流信号能够穿过较薄的金属层以及较厚的非金属层，实现对金属构件较深处的检测。

与传统涡流传感器相比，PEC传感器激励线圈激发的磁场幅值大，在大提离下仍然可测得检测信号；同时PEC传感器覆盖面积大，能够检测到大面积的金属腐蚀[3]。

1 脉冲涡流检测原理

脉冲涡流检测原理示意如图1所示，将信号源产生的具有一定脉冲宽度的方波电流施加于激励线圈，在方波电流的上升沿与下降沿瞬间，激励线圈中会产生一个快速衰减的一次磁场，衰减的一次磁场在金属试件中产生感应涡流[4]。感应涡流的变化产生二次磁场，检测线圈将感应到的变化的二次磁场信息转为电压信息。若金属试件存在缺陷，则会导致感应涡流发生变化，最终检测线圈感应到的电压信号发生变化，通过对变化的电压信号进行分析从而确定金属试件的缺陷情况[5]。

图1 脉冲涡流检测原理示意

检测线圈放大后的感应电压信号如图2所示，对于多匝导线的检测线圈上感应电压信号的计算，可采用有限元的数值计算方法。

图2 检测线圈放大后的感应电压信号

可通过理想化方式将线圈铜线的横截面看成每一个点的构成，运用麦克斯韦方程，则每个点的瞬态感应电压为

(1)

式中：B为磁感应强度；A为矢量磁位;l为理想化时单匝线圈的长度单位。

因此单匝线圈的瞬态感应电压为

Vf=∬Vpit(r,z,t)drdz/((∬drdz)

(2)

式中：r，z为检测线圈的半径，高度；t为积分时间。

利用有限元的方法计算，式(1)为

(3)

式中：r0为有限元检测半径；h0为有限元检测线圈与导体表面间的距离。

将式(2)代入式(3)可得检测线圈上的瞬态感应电压[6-7]

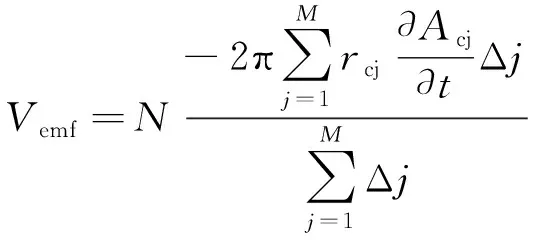
(4)

式中：Δj为第j个有限元的面积；rcj为有限元的中心距离；Acj为中心矢量磁位；N为线圈的匝数。

2 传感器设计及仿真

系统总体设计流程如图3所示，上位机通过控制数据采集卡产生幅度、频率以及占空比均可调的双极性脉冲信号，脉冲信号通过H桥电路后,产生脉冲电流驱动激励线圈，激励线圈放置于带包覆层铁磁性材料的上表面，检测线圈将采集的二次磁场信息转化为电信号，电信号通过信号调理电路进行放大、滤波的调理，调理后的信号通过数据采集卡进行采集，最终通过串口传送至上位机，上位机对采集到的信号进行显示、分析、计算与存储。

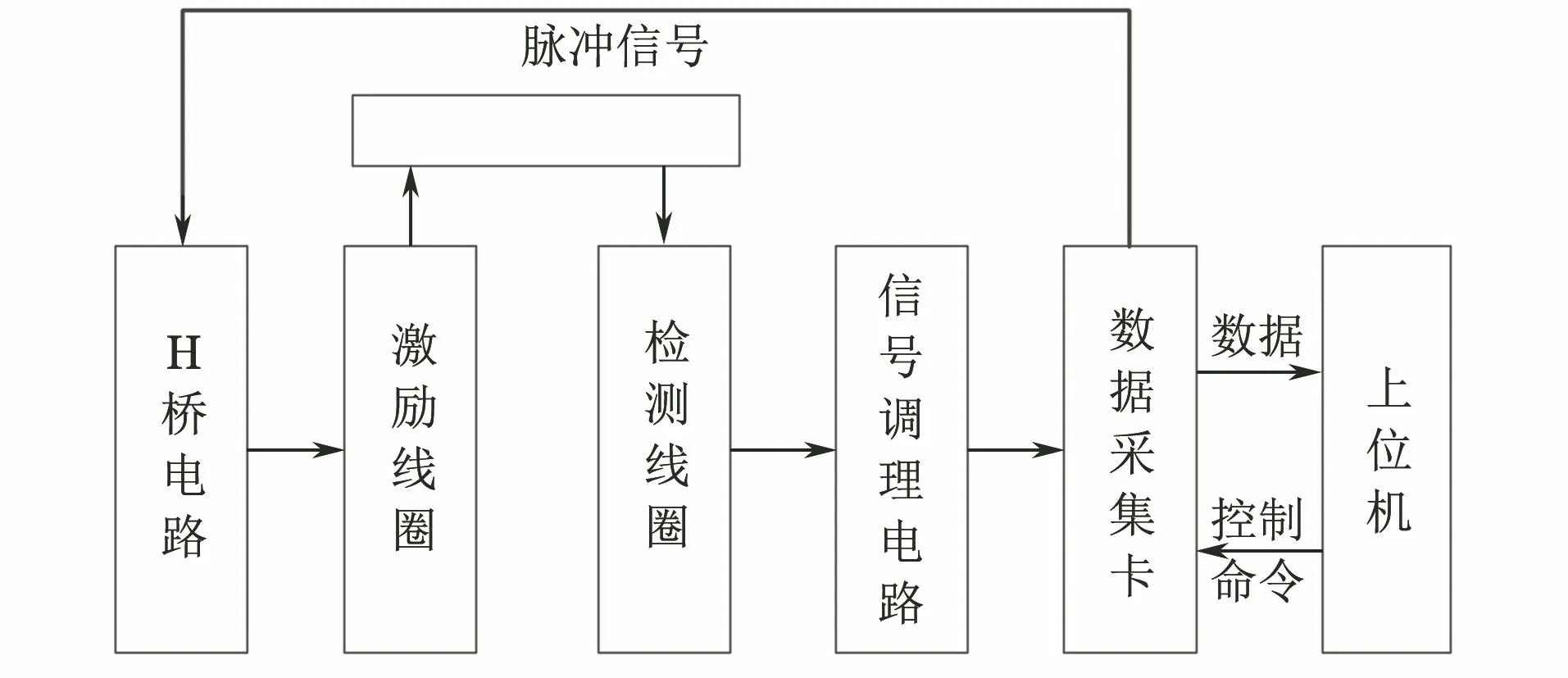
图3 系统总体设计流程

根据涡流信号时域与频域特征值的实时变化情况，检测当前材料是否存在缺陷，通过涡流信号峰值与铁磁性材料厚度之间的对应关系，建立峰值信号与厚度之间的数学模型，进行最佳曲线拟合，得到两者之间的数学关系式，并对材料的板厚进行反演计算,确定材料的厚度信息。

传感器采用复合式结构设计，通过两个激励线圈的联合使用，对激励线圈 1加载一个较大的激励电流，并且同时在激励线圈2加载一个较小的反向电流,使得激励磁场的空间范围得到约束，可实现磁场聚焦的作用。采用复合式激励的方法解决了单个线圈容易受外界电磁信号干扰，以及因大激励电流带来的磁场范围过大的情况，保证了采集信号的稳定性与缺陷检测的精确性，仿真步骤如下。

2.1 搭建仿真模型

在COMSOL软件中搭建的传感器模型如图4所示，激励线圈与检测线圈均等效为圆柱体模型，被测金属试件简化为正方体模型，将空气场简化为球体模型。以三维结构建模，传感器组成部分的参数如下：检测线圈的内径为8 mm，外径为15 mm，线径为0.31 mm，匝数为600匝；激励线圈1的内径为20 mm，外径为28 mm，线径为0.81 mm，匝数为400匝；激励线圈2的内径为34 mm，外径为38 mm，线径为0.31 mm，匝数为200匝，线圈高度均为15 mm。空气场半径设置为150 mm，设置金属试件为边长100 mm，厚度10 mm的正方体。

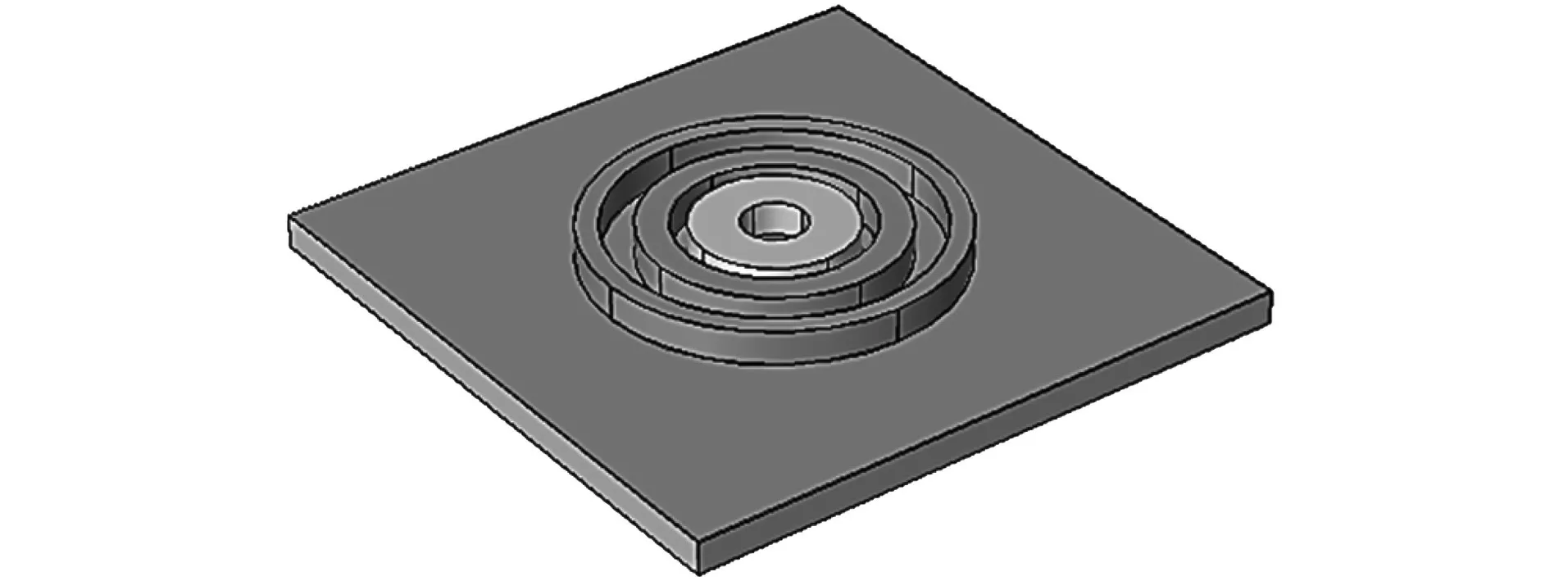
图4 传感器模型

2.2 添加物理场

添加物理场前对模型的材料进行如下选择：空气场模型材料为空气，线圈为绝缘纯铜漆包线，线圈材料为铜，金属试件材料为钢。在COMSOL软件中，选择物理场中的磁场模块，研究类型为瞬态研究，用于计算场变量随时间变化的情况。最后选择模型边界为狄利克雷边界，设置磁矢为0。

2.3 划分模型网格

对有限元模型进行网格划分，划分选择自由剖分的三角形网格类型，网格划分越密，则计算结果越精确，仿真越接近真实情况，同时不同的网格划分程度也有助于提高工作效率。针对不同研究内容进行不同疏密的网格划分。模型网格划分示意如图5所示，选择传感器及被测金属试件的网格划分较密，其余部分自由划分网格。

图5 模型网格划分示意

2.4 求解仿真模型

网格划分完成后，对激励线圈1施加脉冲激励电流为2 A，对激励线圈2施加激励电流为1 A，占空比均为50%，对线圈1与线圈2施加相反方向电流，求解仿真模型。激励线圈1施加的激励电流示意如图6所示，检测线圈感应电压仿真结果如图7所示。

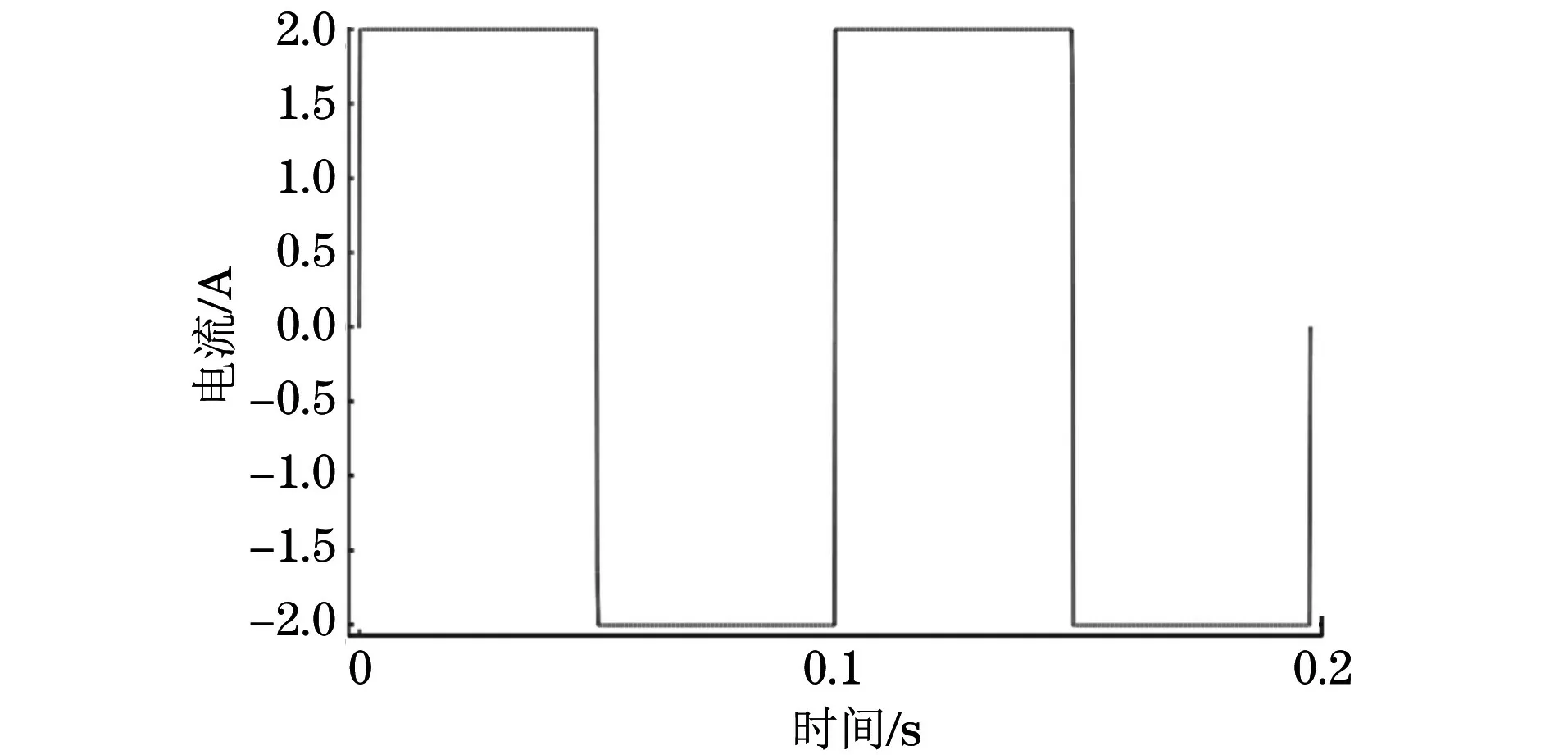
图6 激励线圈1施加的激励电流示意

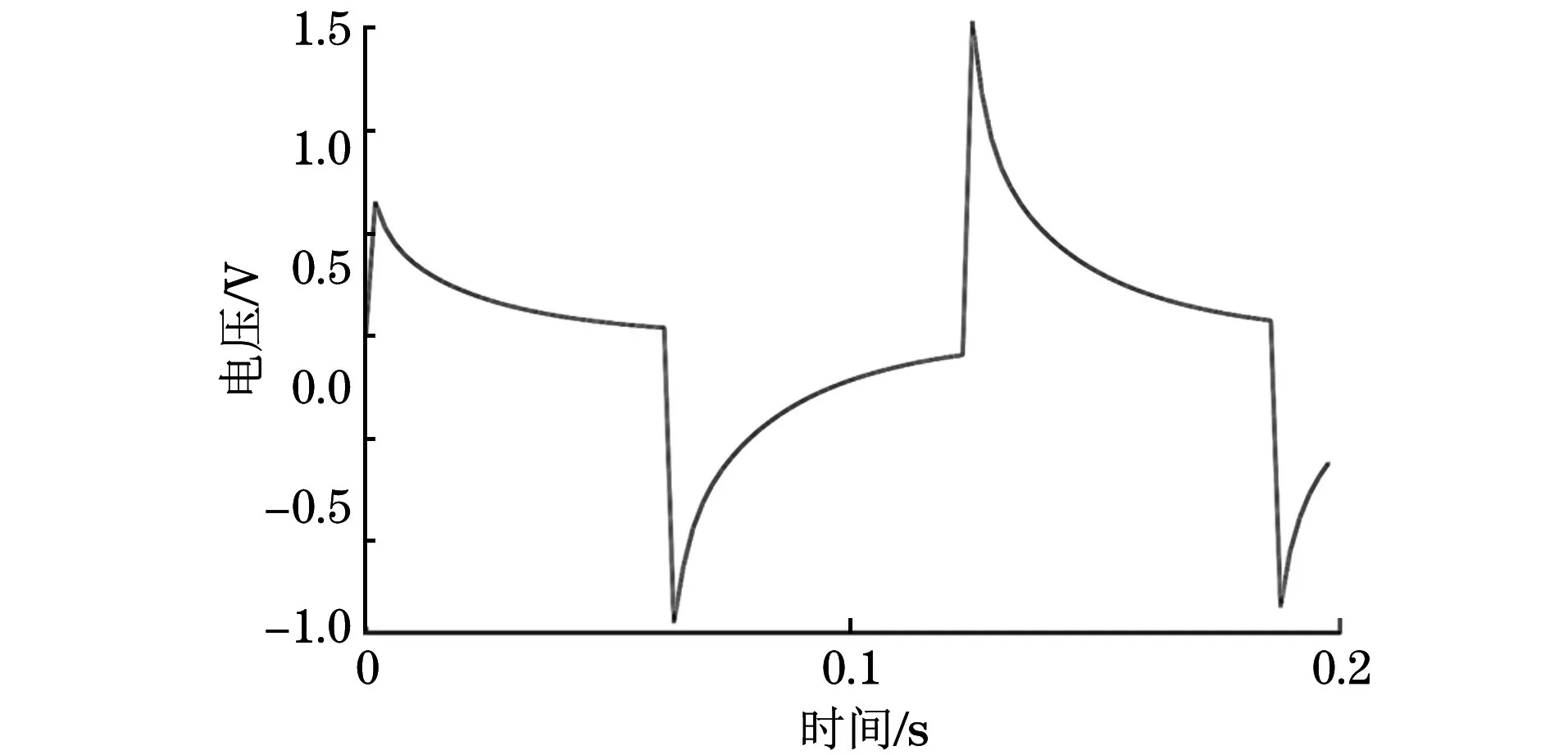
图7 检测线圈感应电压仿真结果

搭建单个激励线圈的传感器模型，设置其激励线圈尺寸与激励线圈1的尺寸一致。对两种不同激励线圈传感器进行仿真，保证金属试件模型以及缺陷深度一致，仿真所得峰值电压数据如表1所示。

表1 仿真所得的峰值电压

分析数据可知，单激励线圈传感器所得的电压信号峰值大于复合式传感器的，但是无缺陷时与存在缺陷时的电压信号差值相对更小，峰值变化相对于复合式线圈较小，因此采用复合式传感器在检测缺陷时更加精确，更具有检测优势。

3 试验结果与分析

实验室加工了一批Q235钢板试件，对钢板进行挖槽、切割等缺陷处理，采用岩棉板模拟包覆层材料，保持岩棉板包覆层材料厚度为20 mm不变，利用脉冲涡流检测系统对钢板进行缺陷检测，观察上位机软件界面中电压峰值的变化(见图8)。

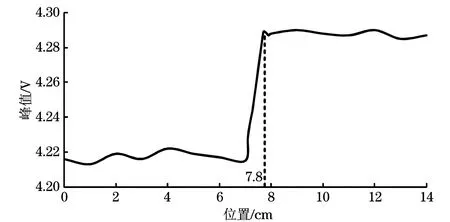
图8 上位机软件界面中电压峰值的变化示意

传感器移动方向示意如图9所示，保持传感器以1 cm·s-1的速率沿钢板边界横向移动，以钢板边界位置记做0 cm，由图8可知，涡流信号的峰值在距离钢板边界位置7.8 cm处发生变化，且变化趋势相同，由此可确定金属试件在该处位置存在厚度变化，即该处有缺陷。

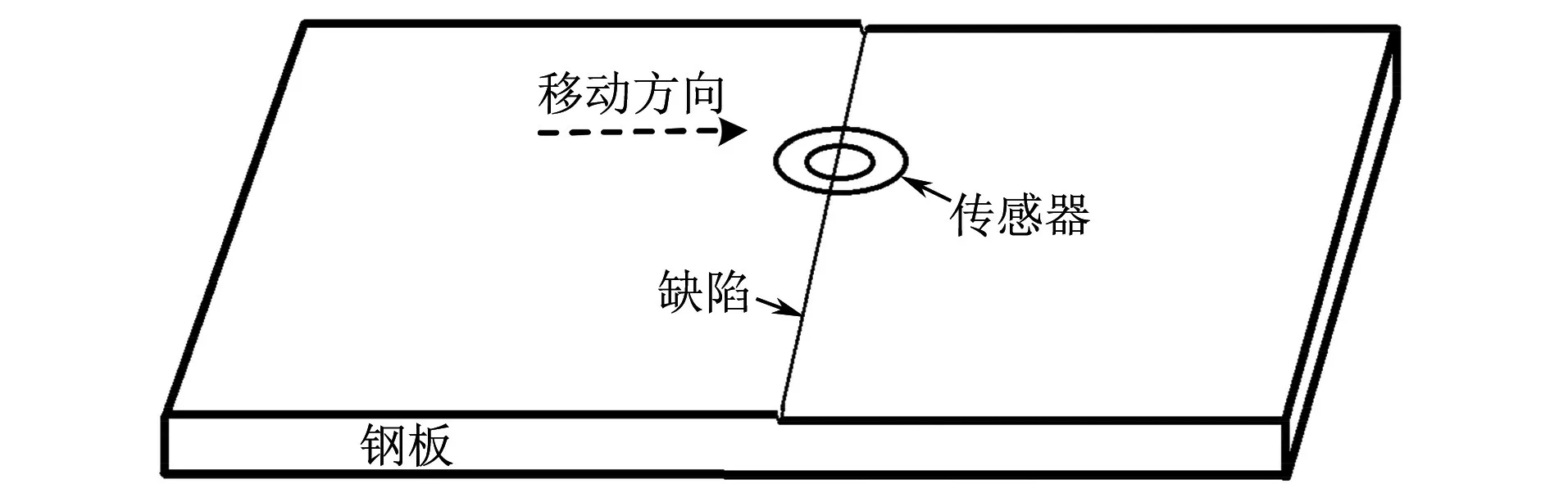
图9 传感器移动方向示意

针对不同程度的缺陷，对其时域信号进行傅里叶变换,得到其频域分布如图10所示。

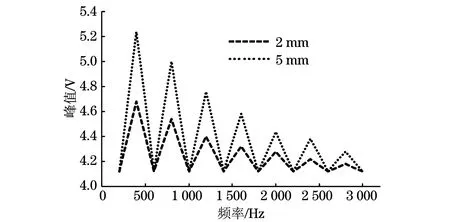
图10 缺陷检测信号频域分布

对检测信号的频谱进行分析，提取其基波分量及谐波分量的幅值，不同缺陷深度的钢板对应不同的信号幅值(见表2)，缺陷深度由2 mm增加到5 mm时，基波幅值变化最大。则可以在频域范围内通过检测基波的幅值来确定钢板的缺陷情况。

表2 不同缺陷深度的钢板对应的信号幅值

采用岩棉板模拟包覆层材料，保持岩棉板厚度20 mm不变，钢板厚度分别为12,10,9,8,6,5 mm，保持钢板试件阶梯状放置，用检测系统对不同试件进行检测，保存不同厚度试件的涡流信号峰值数据，取3次试验结果的平均值，所得拟合曲线如图11所示。

图11 峰值曲线拟合

选择拟合函数为多项式拟合，拟合方法为最小二乘法，阶数为3阶，则拟合所得多项式为

y=-4.599x3+87.786x2-563.74x+1 217.042

(5)

对钢板试件进行测量，保存峰值数据，并代入多项式计算得出未知厚度的钢板试件数据，取3次测量结果的平均值，所得结果如表3所示。

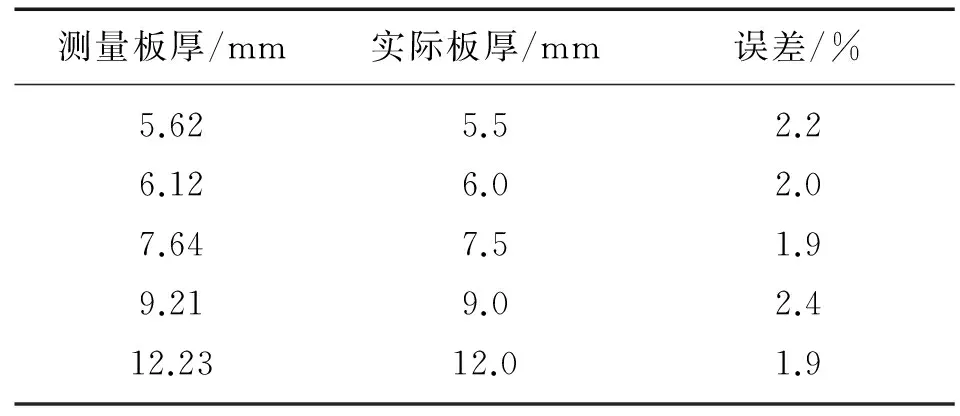
表3 钢板厚度数据测量结果

4 结语

针对油气田行业带包覆层铁磁性材料缺陷不易检测的问题，设计开发了一套金属材料缺陷的脉冲涡流检测系统。通过新型传感器的仿真与设计，实现了缺陷位置的精确测定，同时系统可以有效测量金属材料的厚度。试验结果表明，该检测系统能够检测包覆层小于20 mm的金属材料缺陷，厚度检测精度误差达到3%以内。