残余应力的表征
2020-10-17巴发海刘宇希
巴发海,刘宇希
(上海材料研究所 上海市工程材料应用与评价重点实验室,上海 200437)
1 残余应力的概念与本质
GB/T 7704—2017 《无损检测 X射线应力测定方法》给出了比较明确的残余应力定义:在没有外力或外力矩作用的条件下,构件或材料内部存在自身保持平衡的宏观应力。每个截面上的内力平衡,相当于每个轴内力矩相互抵消,如果平衡破坏,将产生宏观尺寸的变化。
特点1: 局部均匀。残余应力本质即指在宏观材料区域(很多个晶粒范围)内几乎均匀(大小和方向)分布的应力。但由于工程材料的不均匀性和各向异性,实际是宏观的局部均匀。
特点2:多相材料不同相的应力是不同的,但总体上(总和)是保持宏观平衡的。如α+β双相黄铜经3%的拉伸后,α相为压应力,β相为拉应力;钢中变形后的铁素体为压应力,渗碳体为拉应力。而总应力则是各相应力的代数和。
特点3:在工程上,残余应力可以和外部服役应力产生叠加效应,恶化服役应力的状态,而这往往是材料或构件早期快速失效的重要原因之一。如腐蚀环境中可引起应力腐蚀,大锻件热处理不到位时的应力残留过大可引起滞裂。一般滞裂的时间不确定,与有无叠加外力无关。
残余应力测定中主要涉及到4个应力概念:正应力(σ)为垂直于考察截面(某个测试平面)的应力分量;剪应力(τ)为相切于考察截面(某个测试平面)的应力分量;主应力为材料内某一点以n=(n1,n2,n3)为法向量的微面积元上τ=0时的正应力,即不存在剪切应力的垂直于考察截面(某个测试平面)的正应力。
在测试中,可能测试的是某个方向的正应力,但并不等同于内应力。内应力实际上是一个主应力的概念。测试中可通过设置不同角度计算各主应力的大小和方向。应力测试结果是否等同失效分析中所关注的失效应力,应具体分析和判断。
三维应力与二维应力:直角坐标系中某一点以n=(n1,n2,n3)为法向量的微面积元上的全应力S可由9个(3个正应力分量+6个切应力分量)分量构成或三个矢量完整表示(称为二阶应力张量,见图1)。根据应力张量特性,在外界作用不变的情况下,一点的主应力状态是不变并客观存在的,与坐标轴的选取无关,只与3个主应力和代表主应力方向的空间角度相关。根据张量的基本性质,应力张量可以叠加和分解,存在3个主轴(主方向)和3个主值(主应力)以及3个独立的应力张量不变量。主应力即作用在“主平面”上的应力。主应力作用的方向称为主轴1,2和3,则3个主应力分别为σ11,σ22,σ33。对于任何一个应力状态,都可以定义一个坐标系,该坐标系的轴垂直于仅作用有法向力且没有剪切力的平面。这些平面称为主平面。
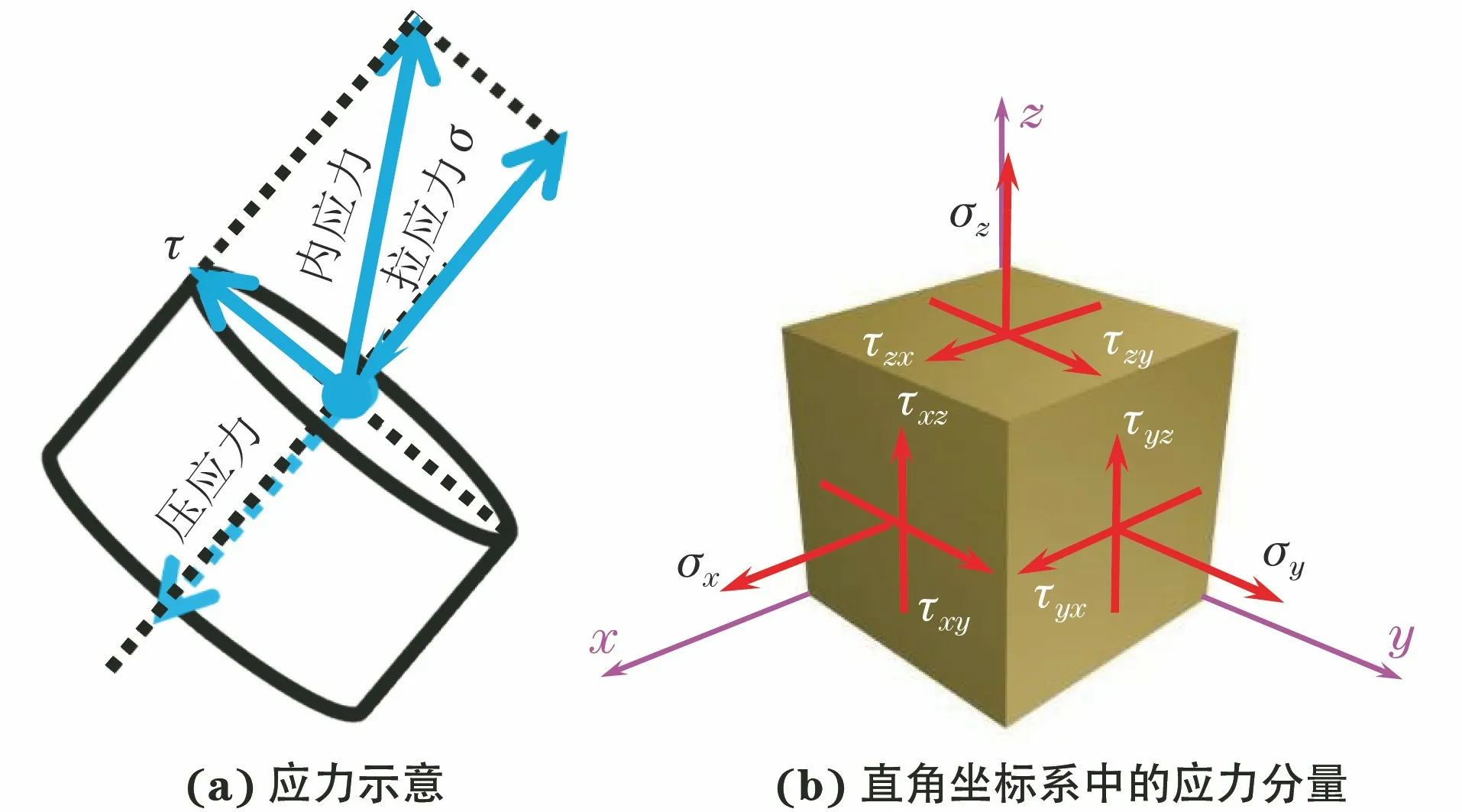
图1 直角坐标系中单元体的应力分量示意
如果表示一点的应力状态的9个应力分量为已知,则过该点的斜微分面上的正应力σ和切应力τ都将随法线N的方向余弦而改变(见图2)。特殊情况下,斜微分面上的全应力S和正应力σ重合,而切应力τ=0。这种切应力为0的微分面就是主平面,主平面上的正应力即主应力。主平面的法线方向称为应力主方向或应力主轴。可知,测试时选取不同的坐标系和法向,尽管主应力的状态不变,但不同测试方向的正应力和切应力并不相同。因此,应根据实际情况选择坐标系,选择测试方向。
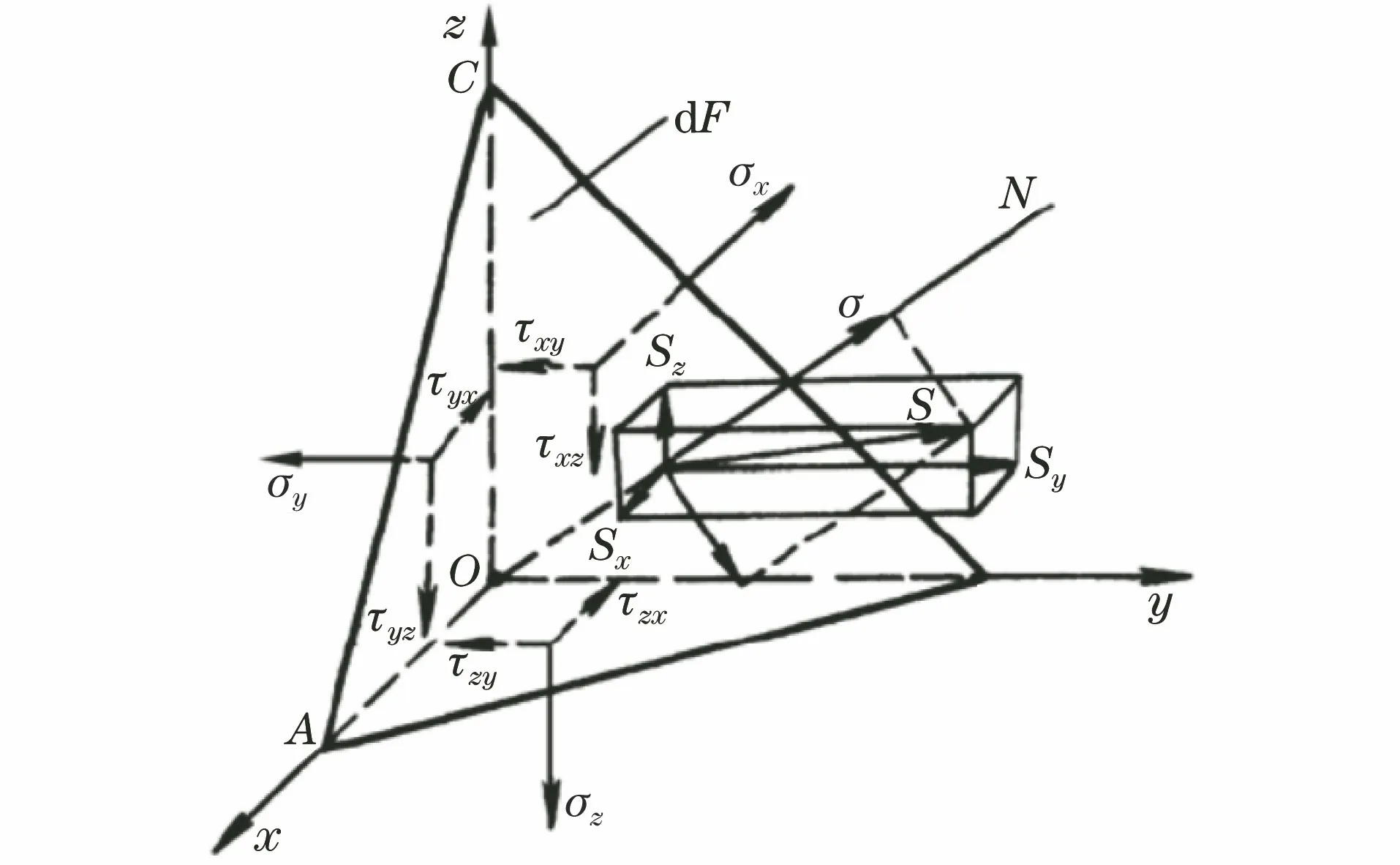
图2 任意斜切微分面上的应力示意
在二维平面应力的情况下,存在两个彼此垂直的主应力σ11(x方向)和σ22(y方向),平面应力示意如图3所示。主应力或正应力需要进行计算分析和判断。

图3 平面应力示意
2 残余应力的测量原理与方法[1]
对于多晶体材料,应力所对应的宏观应变被认为是相应区域里晶格应变的统计结果。通过X射线衍射测定衍射角2θ的微小变化,依据布拉格方程,反过来计算晶格平面的均匀位移(晶面间距变化)(ε=d/d),再依据弹性力学原理计算出应力的大小。也就是说,面间距的相对变化(Δd/d)反映了由残余应力所造成的晶面法线方向上的弹性应变(ε)。X射线衍射应力测试的正交坐标系如图4所示。
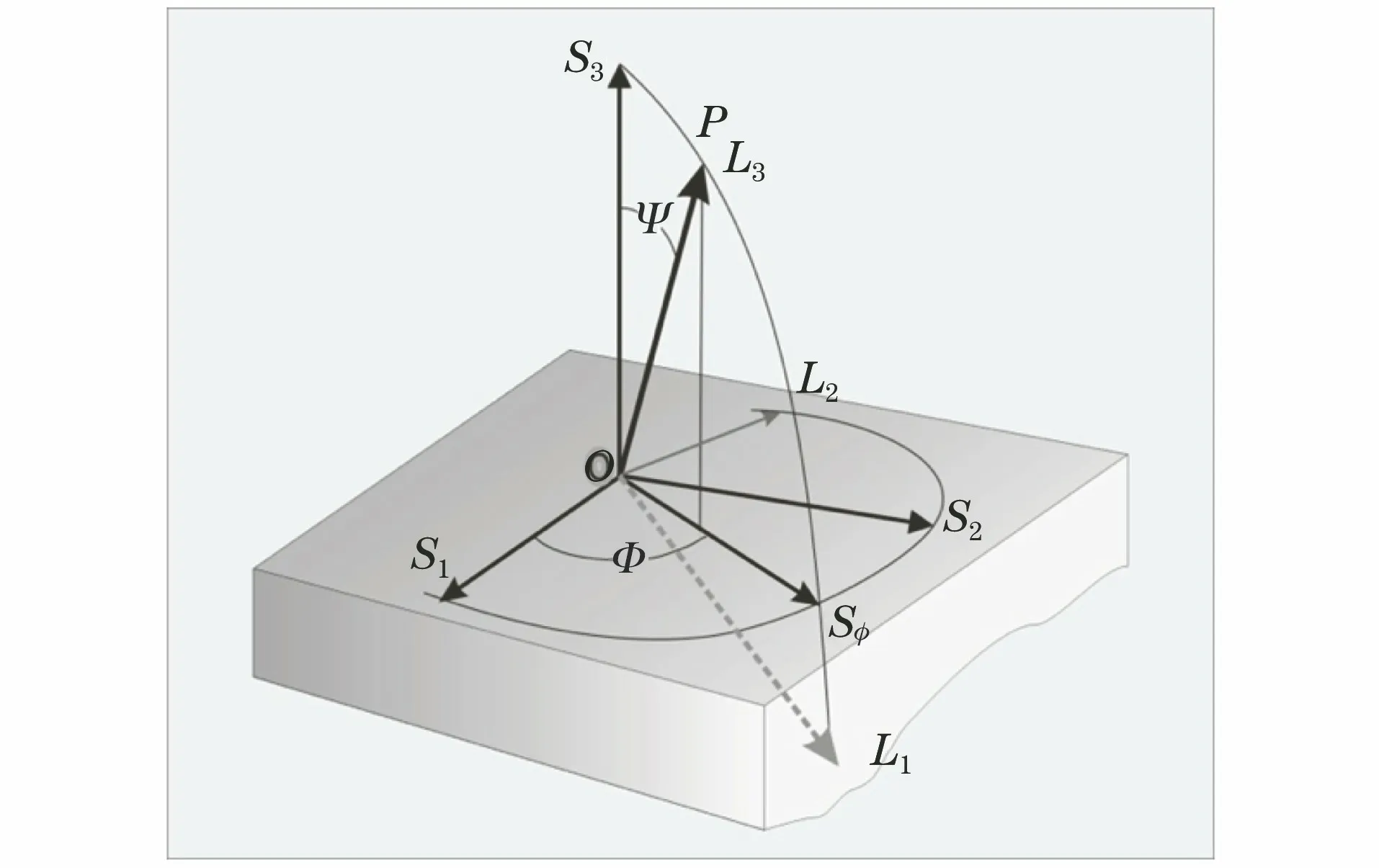
图4 X射线衍射应力测试的正交坐标系
晶粒某方位的晶格应变为
(1)
式中:dφψ为晶面法线由φ和ψ角定义的{hkl}晶面间距;d0为材料无应力状态{hkl}晶面晶距;θ0为材料无应力状态{hkl}晶面对应的布拉格角;θφψ为φ和ψ角定义方向上的应变对应的衍射角的1/2。
依据张量坐标转换和线弹性力学的胡克定律,φ,ψ方向某{hkl}晶面的应变可表示为
(2)
则所求测试平面上的应力分量可表示为
σφ=σ11cos2φ+σ22sin2φ+τ12sin2φ
(3)
τφ=τ13cosφ+τ23sinφ
(4)
那么总应变就可表示为
(5)

可知,OP方向的总应变与三个平面上的主应力以及φ,ψ有关。从材料力学的角度看,要计算的是主应力以及所测试平面上的两个应力分量。
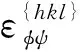
(6)
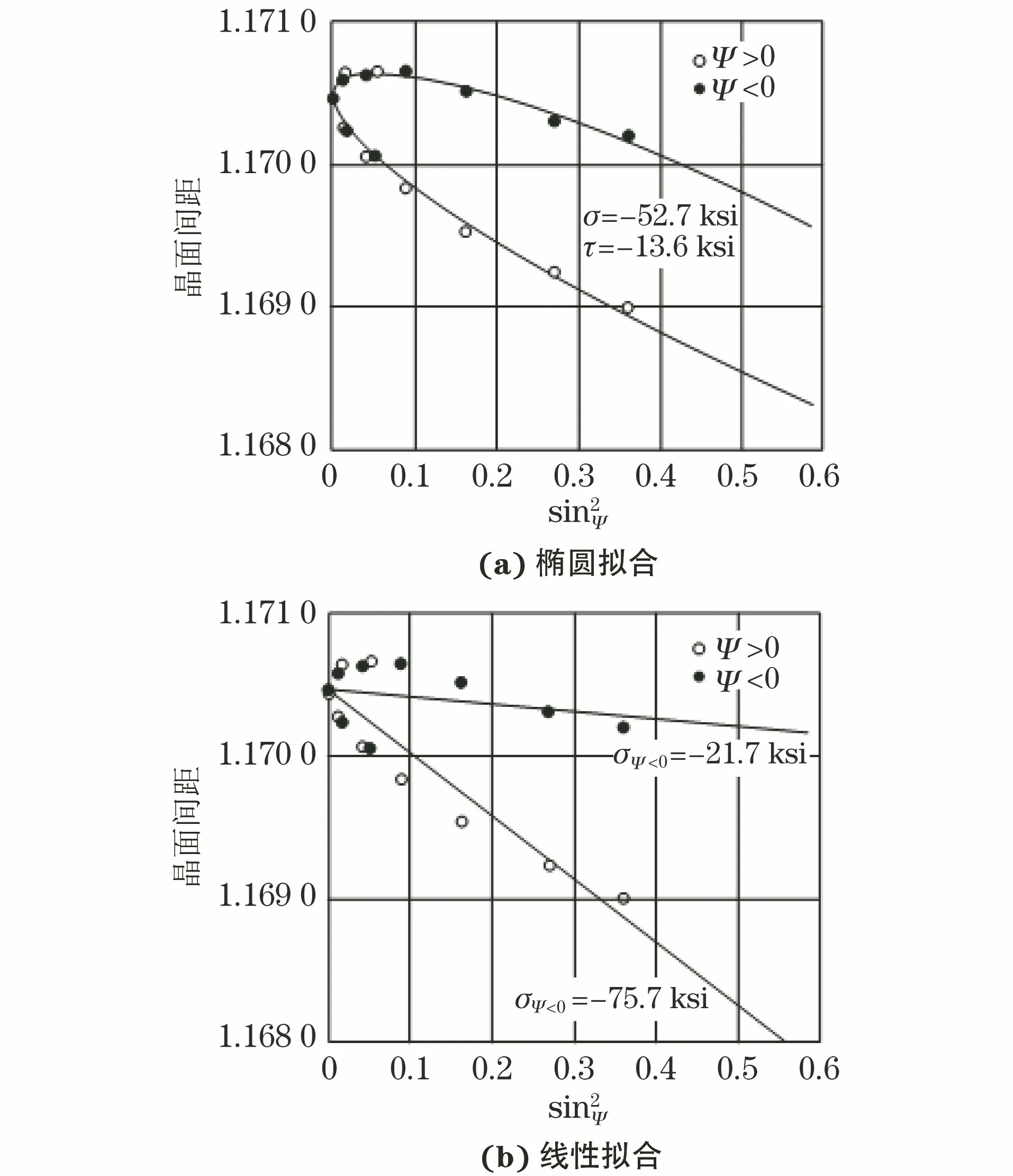
图5 椭圆拟合和线性拟合的数据偏离对比
σ33≠0,且τ13,τ23不为0,为三维应力条件。此时可通过设置不同的参数求出各主应力和应力张量不变量σ11+σ22+σ33。为了表征完整的应力张量(三轴应力),需要在6个方向上进行应力测量(至少需要3个φ方向)。当测量方向受样品几何形状限制时,对于任何参考系,都可以使用0°,45°和90°处的测量值来计算双轴情况下的莫尔圆,并求出各主应力和切应力。该方法也可以应用于三轴情况。应该指出,在平衡状态下,σ33≠0表示没有垂直于自由表面的应力。然而,该表面法线方向上,在表面以下的某个深度处仍然存在应力。因此,对于一些深度穿透的测量(数十微米),可能会出现非零的应力值。如磨削表面在垂直表面方向的残余应力分量为0,表面是二维平面应力状态。但是影响零件使用性能的是零件表面下一定深度范围内的零件表面层的残余应力状态。磨削表面层与其他切削表面层相比,具有更复杂的应力状态。磨削表面层的残余应力状态不是简单的二维平面应力状态,基于三维应力计算表明[2],主应力不平行或不垂直于磨削表面,三维应力和主应力的计算结果如表1所示。因此,在失效分析中,当预期应力和测试结果偏离较远时,应考虑主应力和切应力的作用。

表1 三维应力和主应力的计算结果
