基于APDL的摆线针轮传动小周期动态啮合仿真分析
2020-10-17孙晓超张迎辉卢琦崔迪何卫东
孙晓超,张迎辉,卢琦,崔迪,何卫东
(1.辽宁加宝石化设备有限公司,辽宁 营口 115000;2.大连交通大学 机械工程学院,辽宁 大连 116028)*
RV(Rotate-Vector)减速器是由渐开线齿轮和行星摆线针轮组成的两级减速传动机构,具有传动比大、体积小、刚度大、承载能力大、传动精度和传动效率高等优点,广泛应用于工业机器人关节驱动装置中[1-2].摆线针轮传动副啮合力的大小作为影响RV减速器传动精度的重要因素,受到学者们的广泛关注.张东生[3]等在变形协调原理的基础上,提出了摆线针轮传动动态受力分析理论,在全域内找到了最大接触力和最大接触应力,突破了传统方法只能计算一个特殊位置的局限性.何卫东[4]应用赫兹理论,考虑到摆线轮修形引起初始间隙的影响后建立了各个接触齿对受力与接触变性的函数关系,准确计算出针轮同时受力齿数及大小.关天民[5]等应用解析法对修形后摆线轮和针齿啮合时的初始间隙进行了准确计算,提出了完整的二差齿针摆传动的有隙啮合受力分析方法,更符合工程实际.郑钰馨[6]等在详细阐述了无针齿套RV减速器摆线轮啮合受力计算方法的基础上,使用密切值法对多参数进行了啮合力影响程度排序,确定了摆线轮厚度、曲柄轴偏心距以及针轮半径为与受力密切相关的参数.姚灿江[7]利用 ANSYS Workbench进行RV减速器摆线轮系啮合传动过程的仿真分析,了解摆线轮系在啮合过程中实际受力状态,明确应力分布区域.梁帅锋[8]等应用轮齿接触分析(TCA)技术阐述了轮齿接触分析计算过程中初始参考点求解的难点问题,求解出传统修形方式下摆线针轮传动的瞬时啮合状态、啮合区域.以上分析均为假设摆线轮处于某一静止状态时的受力情况.李超群[9]等基于Adams虚拟样机技术,发现经过正等距、正移距修形后,沿啮合点法线方向会产生初始间隙,导致啮合齿数减少,最大接触力变大,该分析由于假设零件为绝对刚性,不能得到针摆啮合的接触应力.
本文以受力原理为基础,结合有限元数值方法,求解出RV减速器摆线针轮传动在曲柄轴转动360°时各个摆线针轮啮合齿对的有限元动态仿真受力结果,准确得到RV传动一个小周期运动时的动态接触应力变化规律,并与理论计算结果相比较,来验证有限元模型的可靠性.
1 摆线针轮啮合原理
1.1 内啮合摆线针轮齿廓的形成
如图1所示,以短幅外摆线MM′M″作为轮C的齿廓,M点作为轮B的齿廓,两轮各绕其中心oc和oB作旋转运动,就组成了即内啮合摆线针轮传动.在实际工程中,将M点转化为半径为rz的针齿,轮B为摆线轮.如果针轮固定不动,用一个转臂连接摆线轮的中心oB来带动摆线轮作公转运动,则摆线轮就成为了行星轮,进而构成了摆线针轮行星传动.

图1 内啮合摆线齿廓形成原理
1.2 摆线轮标准齿形方程式
针轮上的针齿为标准针齿,与之相啮合而且没有间隙的摆线齿形称之为“标准理论齿形”.通过建立三个坐标系:固连于曲柄轴的坐标系XOpY、固连于针轮的坐标系XpOpYp、固连于摆线轮的坐标系XcOcYc、传动比关系、几何关系等,最终通过一系列的坐标变换,可以得到摆线轮在固连于摆线轮的坐标系XcOcYc中的标准齿形方程式[11].
(1)
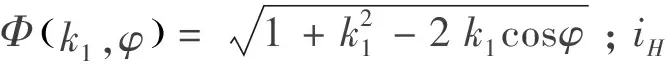
1.3 摆线轮修形齿形方程式
在摆线针轮传动的实际应用过程中,如果按照标准齿形进行装配或工作,会降低RV减速器的使用寿命.为了改善上述情况,实际的摆线轮齿廓不能采用标准齿形,而必须采用修正的摆线轮齿形[10-11].摆线轮的修形方法主要有三种,即移距修形法、等距修形法、转角修形法[12].现阶段关于摆线轮齿形的修形方法主要采用负等距与负移距相组合的修形方法,采用这种修形方法能保证轮齿啮合所需要的间隙要求、并且保证一定的回差要求,取得了比较好的修形效果,得到了广泛地应用.与上文所选的坐标系相同,仍在坐标系XcOcYc建立通用摆线轮齿形方程式,该方程式中包含了所有的修形方法,如下.
(2)
式中,a为偏心距;Zc为摆线轮的齿数;k1′为经过修形的摆线轮齿形短幅系数;Δrp为移距修形量;Δrrp为等距修形量;δ为转角修形量.
RV40E减速器摆线针轮传动几何系数见表1.
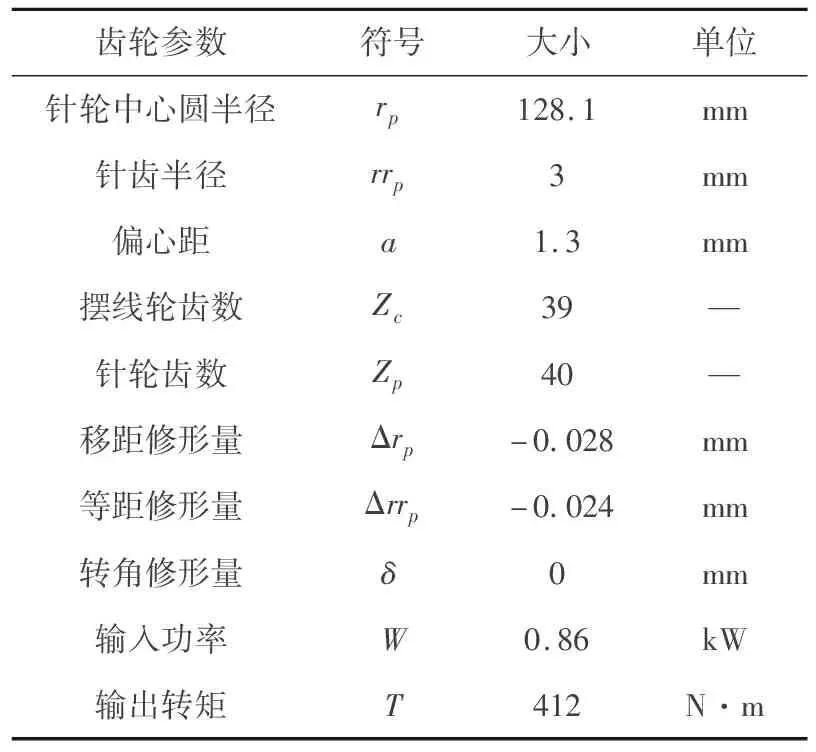
表1 RV40E减速器摆线针轮传动几何参数
2 有限元建模与边界条件确定
2.1 有限元建模
在ANSYS中应用APDL参数化编程语言,生成摆线轮、针齿、轴承、曲柄轴、行星架等一系列零件,进行装配.其中轴承采用ANSYS提供的约束单元类型MPC184,即包括一系列采用拉格朗日算法构建运动学约束的多节点单元,来模拟轴承的旋转运动.在摆线轮轴承孔中心处生成单独的节点,同时选取摆线轮轴承孔内表面节点,在轴承孔中心节点和轴承孔内表面节点之间自动生成多点约束方程,如图2所示.

图2 轴承孔多点约束方程
同理,在曲柄轴曲拐的中心处生成单独的节点,同时选取曲拐外表面上的节点,在曲柄轴曲拐中心节点和曲拐外表面节点之间自动生成多点约束方程.最后,利用铰链连接方法,在摆线轮轴承孔中心点和曲柄轴曲拐中心点之间沿z轴方向建立铰链单元,如图3所示.

图3 轴承模拟连接
对于摆线轮辐和针齿壳等远离摆线轮齿啮合区的部位,对结果影响较小,用稀疏的网格划分代替,以节省计算机资源.这样就导致了这样情况的发生:摆线轮齿的网格密度和摆线轮辐的网格密度发生不连续、针齿的网格密度与针齿壳的网格密度发生不连续.为了将密度不相同的网格区域“系”在一起,ANSYS提供了一种方法,即在接触面上生成若干约束方程,可将一个区域(网格较密)的已选节点与另一个区域(网格较疏)的已选单元连接起来生成耦合约束方程[13].如图4所示,较密网格的摆线轮齿底部节点被“系”在了较疏网格的摆线轮辐外缘单元上;较密网格的针齿周边节点被“系”在了较疏网格的针齿壳针齿槽里的单元上,进而形成了摆线轮整体有限元零件和针齿壳整体有限元零件.

图4 摆线轮齿耦合
摆线齿廓应用Area面生成命令,生成摆线轮齿端面,再由摆线轮齿端面拉伸出摆线轮齿实体,应用六面体单元Solid185单元并应用扫略法直接生成摆线轮齿有限元模型,注意到,由于摆线轮齿的有限元网格划分的精度对有限元计算结果影响很大,同时摆线轮齿上的接触应力计算结果是本文所要分析的重点,故对摆线轮齿的有限元网格进行了细化处理,摆线齿廓上的网格划分段数为50段,网格边线长度为0.3 mm,可见摆线轮齿网格划分的精度很高.在针摆传动中,因为针齿与摆线轮齿直接发生接触,同样为了提高有限元计算结果精度,为了节省计算资源,局部细化针齿的一条边上的网格精度,如图5所示.

图5 摆线轮齿有限元模型
将各个有限元零件的文件全部导入(Import)到一个最终的装配体文件中,行星架和针轮的中心要与整体坐标系的z轴相重合,得到的RV减速器摆线针轮传动有限元装配模型如图6所示.

图6 整机有限元模型
2.2 边界条件的确定
RV减速器的工作方式有多种,图7所示是采用针齿壳固定,太阳轮作为RV减速器输入端,行星架作为输出端;图8所示是采用行星架固定,太阳轮作为RV减速器的输入端,针齿壳作为输出端.对于RV减速器摆线针轮传动部分的有限元动态仿真,其仿真的方式采用图8所示方式.故施加边界条件时,对于行星架来说,约束行星架结构的四周角节点上的全部自由度;对于曲柄轴来说,选取其输入端上的全部节点,释放这些节点的切向自由度并约束径向自由度,对其施加逆时针方向的旋转驱动位移;对于针齿壳来说,选取针齿壳最外圈上的全部节点,释放这些节点的切向自由度并约束径向自由度,因只有一片摆线轮参与啮合,对针齿壳施加顺时针方向的额定工作转矩206 N·m.

图7 针齿壳固定,行星架输出
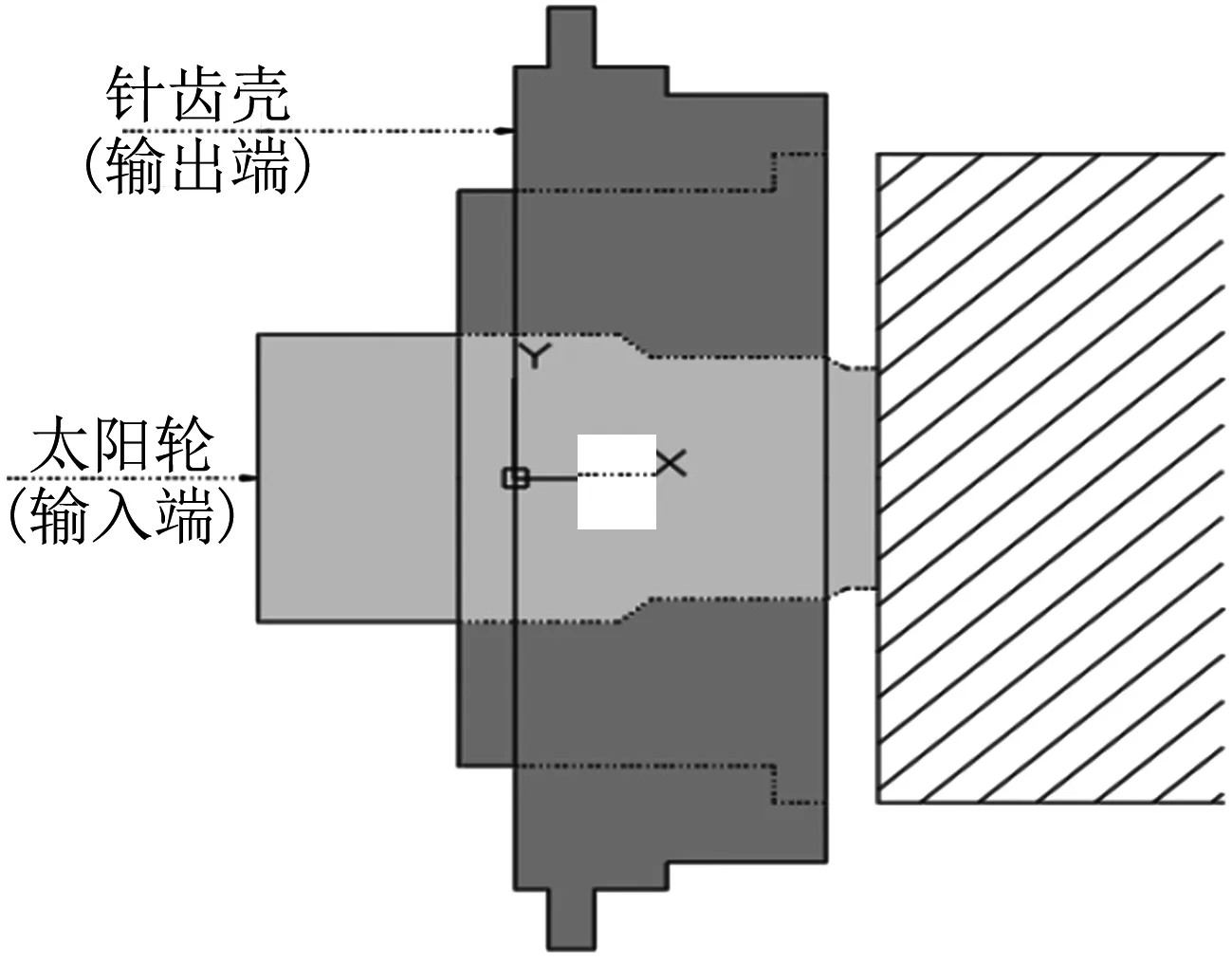
图8 行星架固定,针齿壳输出
3 结果分析
3.1 有限元求解
由于定义的边界条件为行星架固定,针齿壳做输出,因此当输入轴定义匀速转动时,摆线轮做平面运动,针齿壳以设定的传动比降速输出.
设置求解控制选项为:动态小变形求解分析项,求解输出为最后一个载荷步的有限元计算结果;设置求解载荷步数为5,载荷步数自动划分选项打开,最大求解载荷步数为10步,最小求解载荷步数为3步,求解时间取为系统默认的时间1s.求解在一个针摆啮合周期内,各个针摆啮合受力的结果.
3.2 有限元结果分析
根据摆线针轮传动的动态啮合过程,曲柄轴每转动一圈,摆线轮相对于针轮转过一个轮齿,受力区会轮流经过所有摆线轮齿.假设摆线轮轮辐为刚性,则在曲柄轴的每一个转角位置,相应的摆线针轮传动的最大接触应力值都是相同的,即最大接触应力值不随着曲柄轴转角的变化而变化.实际的摆线轮辐是弹性体,它在摆线轮齿受力后会产生弹性变形,摆线轮齿下方的轮辐有薄厚之分,则在曲柄轴的每一个转角位置,轮辐的变形导致了接触状态的改变,因而最大接触应力值随着曲柄轴转角的变化而变化.通过施加上述所确定的边界条件,进行有限元动态啮合仿真,可得到RV减速器摆线针轮传动的最大接触应力值随曲柄轴转角变化的历程曲线,如图9所示.

图9 最大接触应力值随曲柄轴转角变化历程曲线
分析图10所示的历程曲线,从曲线可以看出:最大接触力值随着曲柄轴转角的增加而呈现出上下波动的趋势,波动的最大接触应力值在850 MPa左右,曲柄轴的转角为189°,波动的最小接触应力值在500 MPa左右;波动的曲线存在明显的周期性,即曲柄轴转角在0~180°的范围内为第一个周期,曲柄轴转角在180°~360°的范围内为第二个周期,呈类似的周期性变化.图10为曲柄转动在150°、189°时摆线针轮的啮合状态.

(a)曲柄轴转角150°
以曲柄轴转角位置在189°时的有限元应力分析结果,图11为摆线轮在啮合力的作用下(求解结果放大150倍),摆线轮轮辐的受力变形情况,可以看出由于行星架连接孔的存在,薄轮辐区域在啮合力的作用下发生了较大的弹性变形,最大等效应力为543.08 MPa.在摆线轮受力时,轮辐比较薄的部位摆线轮齿所受到的啮合力相比于理论值就比较小,称为摆线轮柔性区;轮辐比较厚的部位承担了几乎全部的工作载荷,将摆线轮轮辐比较厚的部位称为摆线轮刚性区.图12为在该曲柄轴转角位值,出现最大接触应力值的摆线轮齿啮合接触斑,可以看出该轮齿上的最大接触应力为847.87 MPa,因为摆线轮齿边缘具有一定的应力集中因素的影响,从接触斑上的接触应力分布可以看出,最大接触应力主要分布在摆线轮齿面的边缘附近处,可以猜测出此位置可能是摆线轮齿发生疲劳破坏的危险点.
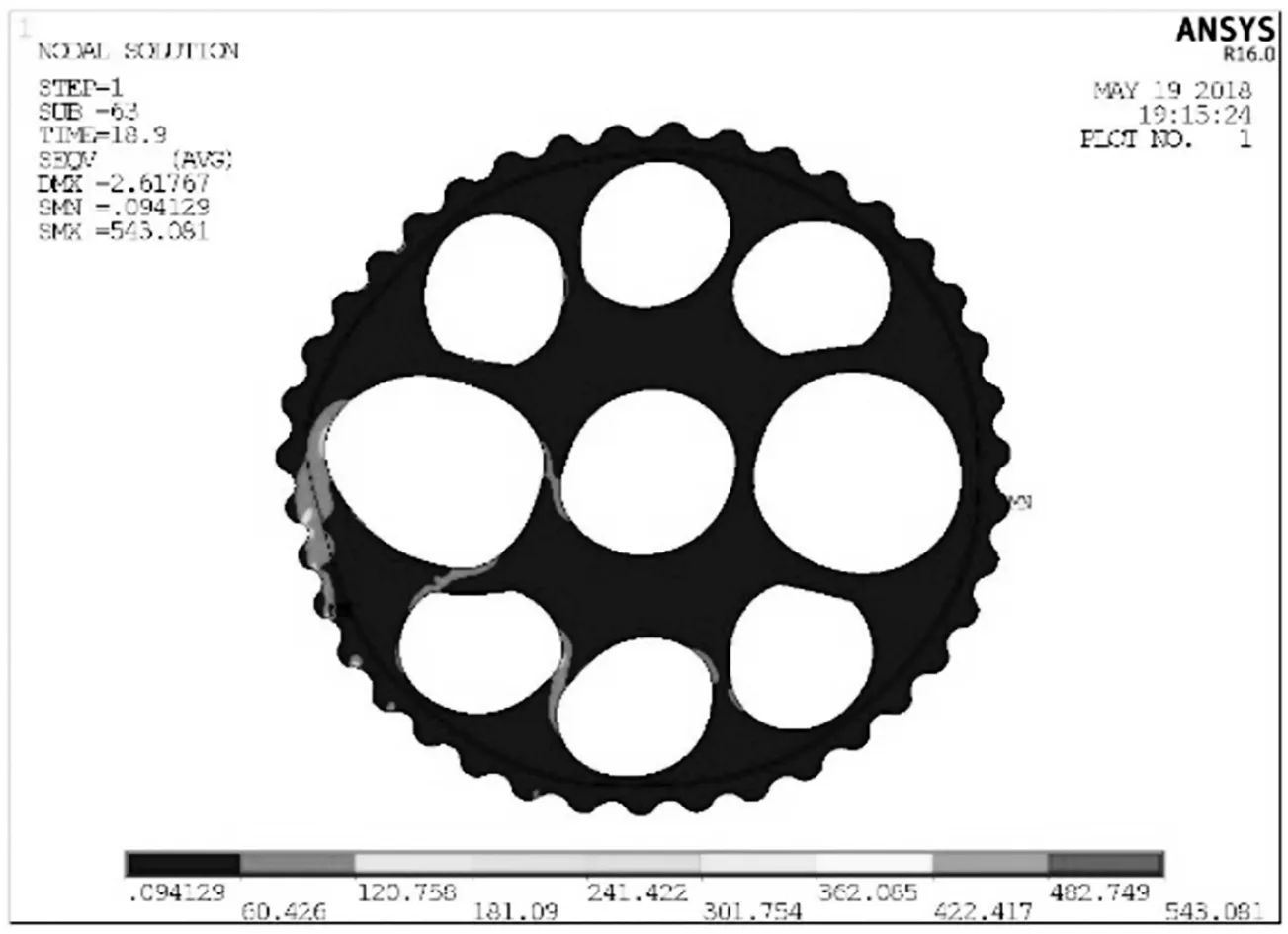
图11 摆线轮Von Stress应力

图12 摆线轮齿接触斑
图13为针齿滚过一个摆线轮齿的表面,其表面接触应力的变化历程,每一个接触位置都对应一个接触斑和接触应力值.按照图示滑动方向,接触斑由轮齿底部沿齿廓曲线移动变化,最大接触应力值为847 MPa.
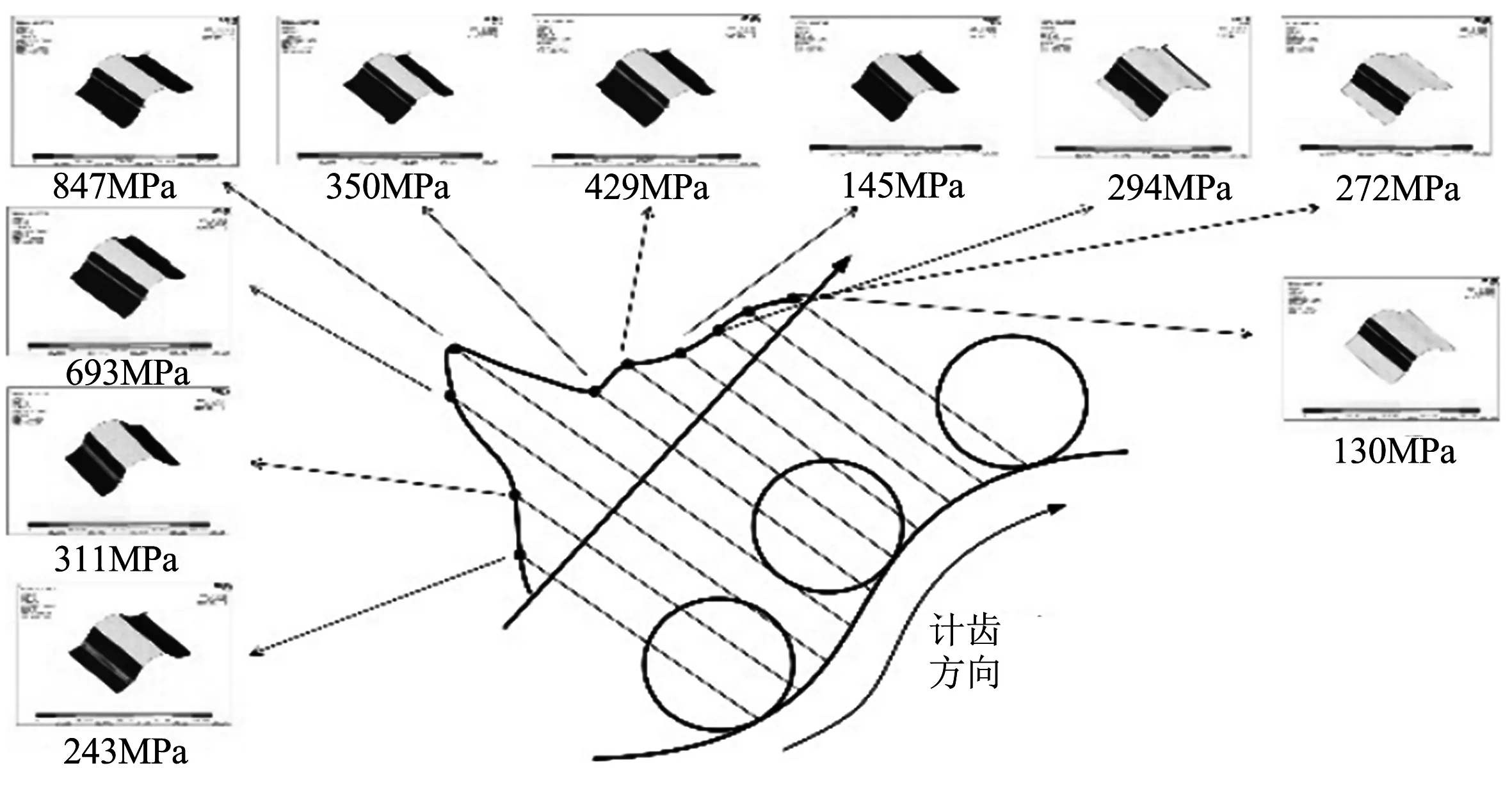
图13 针齿沿摆线轮齿根到齿顶接触应力大小
3.3 摆线轮啮合力结果对比分析
根据参考文献[4]中的计算公式,通过编写计算程序,迭代计算得到RV减速器摆线针轮行星传动的理论啮合力,将其数值与有限元仿真得到的结果进行对比,如表2.
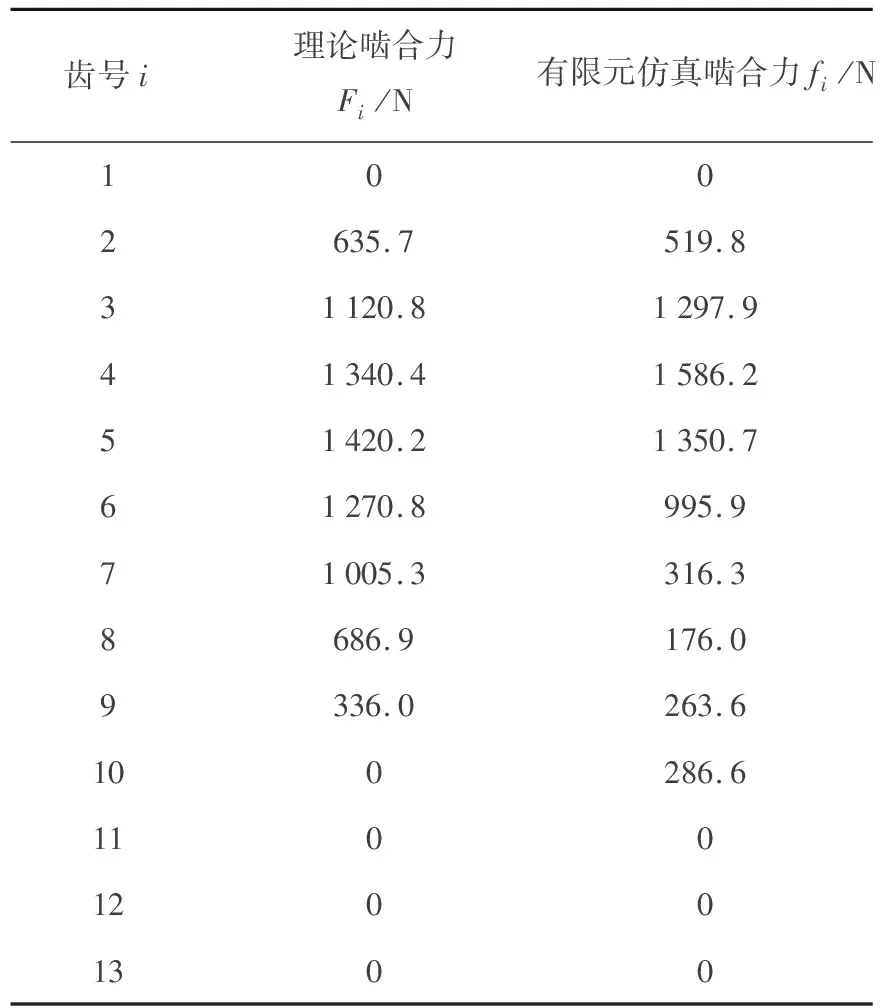
表2 摆线针轮传动捏啮合力对比图表
从表中可知,因为摆线轮轮辐的刚性区和柔性区的存在,导致了摆线轮在受力的时候出现了变形分化,1号~6号摆线轮齿下方的轮辐因为处在刚性区而发生较小的弹性变形,7号~9号摆线轮齿下方的轮辐因为处在柔性性区而发生相对较大的弹性变形.摆线轮在受力的时候,柔性区的摆线轮辐被拉直从而导致摆线轮齿与针齿的接触较轻,故得到的有限元应力仿真结果比理论值小很多;刚性区的摆线轮轮辐因为柔性区轮辐的变形,而被挤得向外凸起,从而导致摆线轮齿与针齿的接触较重,故得到的有限元应力仿真结果比理论值结果大,两段曲线最大值相差约160MPa.2号~6号摆线轮齿成为摆线轮主要受力轮齿,也是摆线轮的主要承载区,因此通过与理论计算结果的比较可以说明有限元仿真得到的结果更接近于实际受力情况,两段受力曲线总体变化趋势较为接近.
4 结论
(1)应用APDL参数化编程语言建立了RV-40E有限元分析模型,进行以针齿壳为输出时曲柄轴转动360°一个针摆啮合小周期的有限元动态仿真;
(2)得到了针摆传动的最大接触应力随曲柄轴转角变化的历程曲线,分析了针齿沿摆线轮齿根到齿顶连续动态啮合的接触应力变化规律,与计算得到的RV减速器摆线针轮传动理论啮合力进行对比,符合接触应力的变化规律;
(3)基于APDL语言建立的参数化有限元模型可快速建立RV-E系列各个型号摆线针轮传动动态接触仿真模型,为理论研究提供方便.
