石墨烯优化固体聚合物电解质电解法分离氢同位素的模拟分析

卫 飞 唐方东 刘佳煜 忻智炜 曾友石 楚鑫新 刘 卫

1（中国科学院上海应用物理研究所 上海 201800）

2（中国科学院大学 北京 100049）

3（上海市计量测试技术研究院 上海 201203）

氢同位素对于现代分析方法和示踪技术非常重要，在环境、能源、生命科学等［1−3］领域有着广泛的应用，因此氢同位素的分离和提纯具有十分重要的应用价值，受到国内外学者的广泛关注。基于同位素在物理及化学性质上的差别，国内外已发展了多种分离方法，如蒸馏法［4−7］、化学交换法［7−8］、电解法［9］和激光分离法［10］等。其中，低温精馏法［4］在重水生产、重水除氚等多个领域均有应用，但其分离系数小，热量消耗大，运行控制要求高，不能广泛商用；化学交换分离技术中的H2O-H2S 交换法［11］虽然分离系数高、能耗较低，但H2S 腐蚀性较强且有毒，具有安全隐患；激光分离法［10］虽然分离系数高，原料利用率高，但其工业规模生产尚未成熟，这促使研究人员不断寻找更为高效、经济、安全的氢同位素分离技术。日本学者 Saito［12］于 1996 年将固体聚合物电解质（Solid Polymer Electrolyte，SPE）用于水电解实验，成功研制了SPE 氚浓缩装置。相比其他分离方法，SPE电解法具有电解效率高、分离能力大、操作安全简便等优点。SPE电解法可应用于低浓度氚化水的富集、含氚废水的处理、低氘水的制备过程中［13−14］，对环境的监测保护具有重要意义。

膜电极是SPE 电解法分离氢同位素的主要部件，由质子交换膜、阴极催化剂和阳极催化剂组成。样品水主要以H2O、HDO和HTO形式存在。在电解过程中，氢同位素在膜电极发生同位素效应，主要有三个步骤［15］：首先，由于氢同位素零点能的差异，H2O 优先在阳极侧发生析氧反应，使得HDO、HTO等保留在阳极液相中；其次，由于H+、D+、T+在质子交换膜的运输过程中存在动力学同位素效应，使得氢同位素离子的迁移速度不同，质量最小的H+会优先到达阴极侧；最后，水合质子在阴极侧由于电极反应速度的差异使得H+优先发生析氢反应进入气相。在整个电解过程中，氢同位素的分离效果主要受到反应温度、电流密度、电极材料和SPE 膜材料的影响［14，16］。不少学者通过调控反应条件和改变催化剂的材料等方式来优化膜电极，但这些传统优化方法并不能显著提高SPE电解法对氢同位素的分离系数（H/D～2，H/T～12）［17−18］。因此，迫切需要一种新型高效的氢同位素分离滤膜来优化膜电极，提升SPE 电解法的分离效果。

石墨烯及其衍生物（双层或多层石墨烯）因其出色的光学、电学、力学特性，在材料、能源、环境等领域［19−24］引起了极大关注。近年来，石墨烯也为氢同位素的分离带来了新突破，它作为仅允许质子和电子通过的单层原子晶体，在分离氢同位素时表现出非凡的亚原子选择透过性［25−26］。研究人员将单层石墨烯转移至Nafion 膜上，探索了单层石墨烯对质子（H+）和氘核（D+）的选择性，表现出优异的分离效果（H+/D+～10）［26］，优于传统 SPE 电解法的分离能力。这种新型高效的氢同位素分离方法无需添加其他化学物质，能耗低，尺寸小，可转移至质子交换膜上，有望在膜电极中发挥作用，高效提升SPE 电解法对氢同位素的分离能力。

目前，石墨烯在氢同位素分离领域的应用仍处于初级阶段，一些学者选用第一性原理对氢在石墨烯表面的吸附能、穿透势垒进行了计算，对缺陷、化学修饰和溶剂作用等［27−29］对质子传导性的影响进行了理论研究。但将石墨烯应用于SPE电解法分离氢同位素领域的相关研究尚未报道。为了探究基于石墨烯优化SPE膜电极的可能性以及优化后的SPE膜电极在实验过程中对氢同位素的分离性能，有必要建立合适的理论分析模型，对石墨烯在反应时的作用机理进行系统的理论模拟分析，探索在该模型系统下石墨烯对氢同位素的分离能力，为建立新型高效的氢同位素分离法提供理论支撑。

1 模型与计算方法

1.1 模型的建立

SPE膜电极由全氟磺酸离子交换膜及其两面压附的不同电催化剂组成。本文选用双层质子交换膜替代传统膜电极中的单层离子交换膜，并将二维晶体石墨烯转移至这两层质子交换膜之间，建立了“三合一”式膜结构，优化后的SPE的膜电极的模型结构如图1（a）所示。在图1（a）中，膜电极的阳极侧加入一定量的水样后，发生氧化反应生成O2和H+、D+、T+，大量的H+在石墨烯的筛分作用下优先到达阴极侧，通过阴极还原反应析出H2。

考虑到氢同位素离子不是在真空中运动，而是沿着全氟侧链上磺酸基（SO3−）提供的氢键网络运动，使得H+、D+、T+在穿过石墨烯之前会短暂与质子交换膜中的水分子结合，呈现出氢离子在穿透石墨烯过程中的初始状态。然而水合氢离子在温室下几乎不能穿过单层完整的石墨烯结构（穿透势垒大于3.8 eV［27］），同时考虑到石墨烯具有亚原子选择性，H+、D+、T+可从质子交换膜的阳极侧经由石墨烯孔洞穿透到阴极侧，则系统模型简化为：H+/D+/T+-石墨烯分子模型，如图1（b）所示。

图1 模拟系统图(a)石墨烯优化SPE膜电极结构示意图，(b)H+/D+/T+-石墨烯分子模型Fig.1 Schematic diagram of simulation system(a)Graphene optimized SPE membrane electrode system,(b)H+/D+/T+-graphene molecular model

本文涉及的模型均基于密度泛函理论（Density Functional Theory，DFT）［30−31］进行第一性原理计算，选用高斯轨道函数为基组设置，并采用梯度校准函数 B3LYP（Becke［32］的三参数混合交换函数和 Lee，Yang 和Parr（LYP）［33］相关函数）在量子化学计算软件 Gaussian 09［34］计算。选用基组 6-31G（d）计算了石墨烯分子对氢同位素离子的穿透势垒和零点能（Zero-point Energy，ZPE），探究了石墨烯模型对氢同位离子的分离效果。

1.2 穿透势垒的影响因素

在计算过程中，首先考虑石墨烯分子模型对氢同位素离子穿透势垒的影响，而穿透势垒可能受到石墨烯分子结构、尺寸大小的影响，因此计算模型确立的关键是先确定石墨烯分子模型。石墨烯分子模型选用圆形团簇，因为圆形簇的相对稳定性比由相同数目的C 原子组成的矩形簇的相对稳定性约高1.5%［35］。本文分别选取了三种不同尺寸的圆形簇石墨烯模型进行讨论，石墨烯边缘的碳原子用氢钝化来饱和其悬挂键，如图2 所示。可通过对这三种不同尺寸大小的圆形簇进行质子限制穿透路径计算，来确定合适的计算模型尺寸大小。

图2 石墨烯分子模型(C6H6,C24H12,C54H18)Fig.2 Graphene molecular model

石墨烯作为仅能通过质子和电子的单层原子晶体，在分离氢同位素时表现出非凡的亚原子选择透过性。在真空环境下，质子穿过完整石墨烯的能力虽远大于氢原子或比氢原子更大的体系，但因其势垒高于1.5 eV［36］，质子仍很难穿透完整的石墨烯结构，因此有必要考虑几何结构优化或石墨烯缺陷对穿透势垒的影响。

石墨烯在制备过程中或多或少会产生一定量的缺陷。石墨烯的固有缺陷主要包括Stone-Wales 缺陷（SW 缺陷）、单空位缺陷、多空位缺陷等［37］。其中，最容易产生的缺陷是SW缺陷，这类缺陷的形成能量大约为 5 eV［38−39］，已有研究证明 SW 缺陷的存在会降低石墨烯对质子的穿透势垒。相关学者计算了质子穿过SW 缺陷七元碳环中心的穿透势垒，质子对SW缺陷的穿透势垒相较于对完整石墨烯的穿透势垒有所下降，降至0.93 eV［40］。考虑计算完整性，笔者计算了另外两种常见的石墨烯缺陷模型对质子的穿透势垒，考虑到缺陷浓度和计算成本的限制，本文选用C36H15单空位缺陷石墨烯，C30H14双空位缺陷石墨烯进行扩展计算，探究缺陷对穿透势垒的影响。

1.3 氢同位素分离系数的确定

在实验条件下，氢同位素离子穿过二维晶体石墨烯是一个受热活化的过程，其反应速率的常数k满足Arrhenius公式［26］：

式中：k为反应速率的常数，min−1；A为指前因子，也称为阿伦尼乌斯常数，min−1；E为反应的活化能，J·mol−1或 kJ·mol−1；kB为玻尔兹曼常数，kB=1.38×10−23，J∙K−1；T为热力学温度，K。忽略阿伦尼乌斯公式的指前因子作为一级近似，可通过将公式改写为不同氢离子的反应速率常数的比值来确定氢同位素的分离系数，如氕/氘同位素分离系数αHD：

其中：ΔEHD=EH−ED，虽然EH和ED可确定氢离子的穿透率，但氢同位素的选择性仅取决于H 和D 的零点振动能的差值△ZPE（△ZPEHD=ZPEH−ZPED），同理适用氕/氚同位素分离系数αHT。因此，本文通过计算在过渡态时系统零点振动能的差异，来推测基于单层石墨烯优化SPE膜电极模型在电解水过程中产生的氢同位素效应，确立氢同位素分离系数。

2 结果与讨论

2.1 分子结构、缺陷对势垒的影响

质子穿过石墨烯碎片苯环中心过程中的动力学穿透势垒是通过扫描垂直于模型系统平面几何中心的限制穿透路径得到的。在计算限制穿透路径过程中，质子与石墨烯分子中心的起始距离为0.15 nm，扫描路径步长为0.01 nm。计算得到三种不同尺寸圆形簇石墨烯模型对质子的穿透势垒为（1.57±0.02）eV，表明随着石墨烯分子模型尺寸的增加，质子的穿透势垒几乎不发生改变，石墨烯尺寸大小对计算精度无显著影响，而存在的差异主要是由于分子模型的边缘效应［39］所致。表明在不同尺寸的石墨烯分子模型中，苯环中心的孔隙环境与石墨烯的六元碳环类似。综合考虑计算精度和速度，后文选取一个具有相邻苯环带的石墨烯分子模型（C24H12）进行计算。

在实际的穿透过程中，质子不完全从六元碳环的几何中心穿过石墨烯，因此还需对C24H12石墨烯模型和二维平面内的质子进行几何结构优化，再进行扫描路径计算，计算结果如图3（a）所示。发现优化后的质子偏离石墨烯六元碳环几何中心约0.038 nm，距离相邻六个碳原子位置在0.118～0.178 nm 范围内。当质子从 0.15 nm 的垂直距离开始接近孔中心时，H+-石墨烯碎片系统的总能量先减小，直到距离达到0.1 nm 处。随着质子进一步接近孔中心，总能量开始增加，直到达到系统能量最大值为止。

通过几何结构优化，扫描路径计算得到质子垂直于石墨烯分子穿过偏心位置的动力学穿透势垒为1.32 eV，低于质子直接垂直穿过石墨烯几何中心时的势垒15.9%。势垒降低的主要原因是，当允许晶格弛豫时，电荷差异对质子的影响便会显现出来，质子在穿过苯环过程中，允许质子和碳原子之间的键的形成和断裂。

计算得到质子穿过单空位缺陷（图3（b））和双空位缺陷（图3（c））的穿透势垒分别为0.80 eV 和0.47 eV，这表明缺陷的存在会大大降低质子穿透石墨烯的势垒，且与缺陷孔洞的大小有关。质子穿过完整石墨烯的势垒是最高的，其最小孔径为0.290 nm，而对于双空位缺陷中的八元碳环，孔径增加到0.369～0.405 nm，穿透势垒相比于与完整石墨烯的势垒降低了1.10 eV，说明石墨烯中固有缺陷的存在可促进质子的传输。

图3 质子穿过不同模型结构的扫描路径(a)C24H12石墨烯，(b)C36H15单空位缺陷，(c)C30H14双空位缺陷Fig.3 The scanning path diagram of protons passing through different model structures (a)C24H12 graphene,(b)Single vacancy defect C36H15,(c)Double vacancy defect C30H14

2.2 氢同位素的理论分离系数

在计算氢同位素效应之前，需要通过寻找反应过程中的过渡态（Transition State，TS）来计算系统的零点振动能。将单个质子放置在C24H12石墨烯的几何中心位置寻找过渡态，有且仅有一个虚频，对应于质子垂直穿过完整石墨烯模型的振动模式Gra-TS（图4（a））。同理，对于质子穿过缺陷石墨烯结构下的过渡态结构，考虑到单空位缺陷和双空位缺陷在过渡态下对质子的穿透势垒近乎于零，因此，这里只考虑SW 缺陷石墨烯。这类缺陷是由于石墨烯的C−C键旋转而形成的，因此该缺陷的形成并没有使石墨烯分子内发生碳原子的引入或者移除，也不会产生具有悬挂键的碳原子。对于SW缺陷共找到两种振动模式，即存在两种过渡态结构（图4（a））：质子从五元碳环附近穿过SW缺陷石墨烯结构的TS1；质子从六元碳环附近穿过SW 缺陷石墨烯结构的TS2。在这几种穿透路径中，质子都从位置1处经由位置2到达位置3处。

将单个H+、D+、T+分别置于完整石墨烯模型和SW 缺陷石墨烯模型中心附近，计算每个系统在过渡态模型系统的振动频率，统计得到每个系统的ZPE，通过做差得到不同体系间的△ZPE。计算结果如图4（b）所示。当H+、D+、T+分别在完整石墨烯模型的六元碳环中心附近做垂直振动时，其零点振动能的差异分别为：ΔZPEHD-Gra=63.8 meV，ΔZPEHT-Gra=91.6 meV。SW缺陷模型在过渡态TS1下，H+、D+、T+从六元碳环附近穿过SW 缺陷石墨烯时，其零点能差异与完整石墨烯结构接近，而在过渡态TS2下，H+、D+、T+从五元碳环附近穿过SW 缺陷石墨烯时，H+和D+、H+和T+的零点能差异明显高于完整石墨烯结构下的的零点能差异。结果表明：基于模型系统计算出的零点校正可以解释石墨烯对同位素离子H+、D+和T+在传输速度上的差异。

图4 ΔZPE过渡态结构(a)，氢同位素离子在不同石墨烯模型结构中(TS)的零点振动能差异(b)Fig.4 Transition state structure of ΔZPE(a),ΔZPE diagram of hydrogen isotopes in different graphene model structures(TS)(b)

在不同温度（T）下，不同石墨烯结构对H+、D+、T+的理论分离系数，可通过上述得到的氢同位素零点振动能的差值，利用Arrhenius 公式（式（2））计算得出。样品水形态为液态，常压下设定温度控制在273～373 K 范围内，计算结果见表1，有效数字取小数点后1 位。结果表明：温度对氢同位素的分离系数呈负反馈现象，即温度越低，分离系数越高。主要是由于温度影响反应速率，温度越高，反应速率越快，加快了氢同位素离子的渗透作用，从而降低了对氢同位素离子的选择性。因此，在后续实验中可通过降低膜电极的反应温度来提升分离系数。在常温293 K环境下，完整石墨烯对H+、D+的理论分离系数为12.4，而对H+、T+的理论分离系数高达37.5，远大于目前SPE电解法的实验值（H/T≈12［17−18］）。与此同时，观察到SW 缺陷石墨烯在TS2下，对氢同位素分离能力高于TS1，推测SW缺陷石墨烯中存在的五元碳环结构会产生比完整石墨烯中的六元碳环结构更高的渗透势垒，这种五元碳环结构的存在在一定程度上可提升氢同位素离子的分离比。

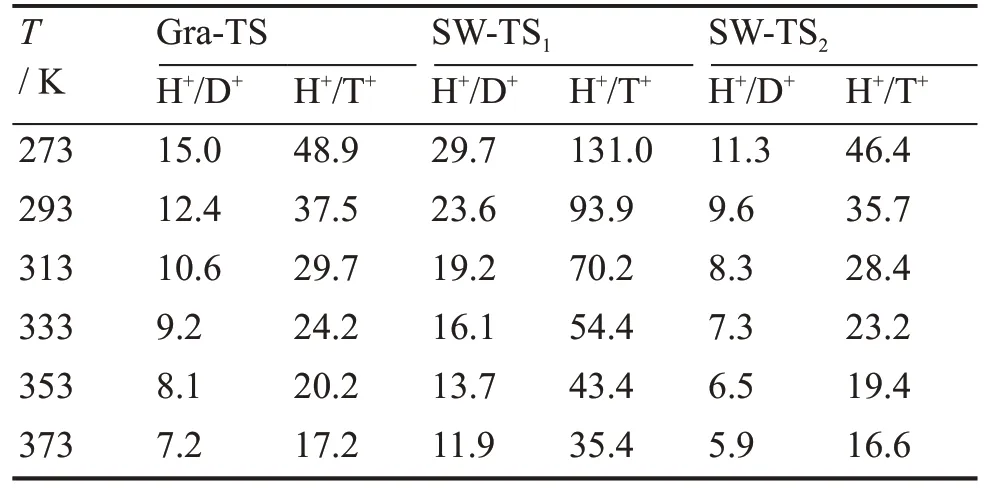
表1 不同石墨烯结构(TS)对氢同位素的理论分离系数Table 1 Separation coefficients of hydrogen isotopes for different graphene structures(TS)at 273～373 K

分离系数的计算表明石墨烯对质子筛分能力远高于目前SPE膜电极中的质子交换膜对水合质子的选择能力，可以预测出将石墨烯应用于SPE电解法，将大大提高SPE 电解法的氢同位素分离系数，这为选用石墨烯优化质子交换膜和提升氢同位素的分离能力提供理论依据。

3 结语

本文使用DFT 理论分析了石墨烯对氢同位素离子（H+、D+、T+）的分离效果，并从穿透势垒、零点振动能差异等角度揭示了分离机制。结果表明建立的H+/D+/T+-石墨烯分子计算模型稳定可靠，模型结构的优化及石墨烯缺陷的存在可降低质子对石墨烯的穿透势垒。同时，计算了过渡态情况下，H+、D+、T+穿过完整、SW缺陷石墨烯分子模型的零点振动能差，推测出在常温293 K时，完整石墨烯结构对H+/D+和H+/T+的理论分离比可达 12.4 和 37.5，远高于 SPE 电解法分离氢同位素的分离系数。本文计算得到的分离系数优于传统SPE膜电极在电解水实验中氢同位素的分离效果，这为选用二维晶体石墨烯材料优化SPE膜电极获得高效氢同位素分离比提供了理论依据，是发展新型氢同位素分离法的可靠支撑，有望建立真正性能优良、安全可靠的氢同位素分离技术。

致谢感谢刘桂民老师对计算工作的指导，感谢木留华同学在计算过程给予的帮助。