基于PSO-FCM方法的我国大中城市房价泡沫研究

□ 吴冠岑 唐 萍 王洪强 牛 星

(1.上海大学 管理学院, 上海 200444; 2.华东理工大学 社会与公共管理学院, 上海 200237)

1998年住房商品化制度改革以来,中国经历了广泛而快速的房价上涨,房价收入比不断扩大。住宅价格的过度增长引起了学者和公众对房价泡沫的担忧。如同其他泡沫一样,房价泡沫是指市场上的实际房屋价格超过其基本价值的部分[1]。如果房地产价格脱离市场基础即均衡价格的持续上扬即为产生泡沫[2]。这样的话房价就可以分为两部分,一部分是由经济因素决定的基础价值,另一部分是对基础价值的偏差[3],该偏差与基础价值的比值便可用来衡量房地产泡沫水平。由于住房市场是一个区域化特征十分明显的市场,房价泡沫在不同城市的表现也是各有特点。

聚类分析可以从收集到的数据出发,根据数据的客观相似性进行探索性的归类,比较适用于房价泡沫类型的判别分析。模糊C均值(FCM)算法是应用最为广泛的聚类算法之一,可以优化目标函数得到每个样本点对所有类中心的隶属度,能更客观地反映现实世界,但其也易受初始值的影响而陷入局部最优[4-5]。粒子群算法(PSO)具有很强的全局搜索能力,可以在一定程度解决FCM易陷入局部最优的缺陷[6-9]。

一、研究方法

(一)住房价格泡沫测度方法

均衡分析方法可以从住房市场供需角度出发测算房地产的基础价值,并在消费者效用和投资者利润最大化基础上比较全面的描述房地产市场的泡沫情况。因此，研究借鉴袁志刚和樊潇彦[10]所提出的房地产市场局部均衡模型,将供求双方均可取得贷款情况下的均衡价格作为本文研究中的基础价值:

(1)

上式中,c表示地产商的单位建房成本,r表示银行贷款利率,Ps、Pr分别表示购房者和地产商归还前期贷款本息的概率,YD表示城镇居民人均可支配收入,θ表示住房贷款额在住房价值中的比例。

住宅商品房平均售价P中超出均衡价格P*的部分便是泡沫,房价泡沫程度b也就可用下式衡量:

(2)

第t年的房价泡沫增长或降低的趋势就可以用泡沫增长率rt衡量;第t年的房价泡沫波动情况可以用波动度ft[11]衡量。泡沫增长率和波动度分别用以下两式计算:

(3)

(4)

(二)粒子群模糊聚类(PSO-FCM)算法

研究从泡沫度、增长率以及波动度三个特征维度对各城市泡沫指标进行聚类分析。聚类之前先根据式(5)和(6)对初始数据依次进行标准差变换和极差变换两步标准化处理,使得每个维度上的数值都落在区间[0,1]上,消除不同量纲对聚类结果的影响。

(5)

(6)

图1 各城市房价泡沫度均值及标准差(2010—2018年)

利用粒子群算法(PSO)优化模糊聚类(FCM)的初始聚类中心时,模糊聚类的目标函数为粒子群算法的适应度函数,当搜索获得全局最优解时,适应度函数为极小值。研究选取Xie和Beni提出的VXB[12]作为FCM算法的聚类有效性函数以确定最佳聚类数目:

(7)

二、实证分析

(一)数据来源

研究选取2010—2018年我国35个大中城市的数据进行实证研究。其中住宅商品房平均售价来源于中国统计年鉴;城镇居民人均可支配收入来源于各地区统计年鉴;单位建房成本按住宅竣工价值与住宅竣工面积的比值计算,来源于中国房地产统计年鉴;购房者和地产商归还前期贷款本息的概率均按1减去不良贷款率计算,来源于中华人民共和国年鉴;住房贷款额在住房价值中比例即住房贷款占比,可按1减去首套房的首付比取值。3～5年期银行贷款利率来自中国人民银行官网。

(二)房价泡沫度计算结果

根据局部均衡泡沫度模型,研究期间样本城市中北京、厦门、深圳在2010—2018年间泡沫度均值很高;上海、杭州、福州、广州的泡沫度均值较高;而天津和南京两地泡沫度均值较低,住房市场泡沫现象较不明显;其余城市泡沫度均值为负,实际住房价格低于住房基础价值。泡沫度标准差方面,北京、厦门、深圳均超过25,尤其深圳在2010—2018年间标准差超过40,各年泡沫情况差异较大;天津、石家庄、太原、长春、上海、南京、杭州、宁波、合肥、海口标准差在10和20之间,其余城市标准差均低于10。初步可见,不同类型城市泡沫表现和发展趋势有很大不同。

(三)房价泡沫聚类指标计算及标准化处理

根据式(3)和(4)分别计算泡沫增长率和波动度,并根据式(5)和(6)将35个城市2010—2018年的泡沫度、泡沫增长率以及波动度进行标准化,同时将样本城市按照排列顺序从1至35依次编号。由于篇幅关系,下表仅展示2018年房价泡沫指标标准化处理结果。

(四)房价泡沫的聚类分析

1.PSO-FCM与FCM方法在房价泡沫上的聚类结果比较

将标准化处理后的数据分别运用模糊C均值算法(FCM)和粒子群优化模糊聚类算法(PSO-FCM)进行聚类分析。

独立运行30次,收集FCM和PSO-FCM算法各自有效性函数值的最优值(30次结果中的最小值)、最劣值、平均值和标准差。结果发现FCM算法在2012年、2013年、2016年、2017年和2018年得到的最小有效性函数值中最优值和最劣值之间均存在较大差异,相应地其对应的最优聚类数目就有所不同。而运用PSO-FCM得到30个最小有效性函数值的标准差依然较小,相较于FCM每次的聚类结果更稳定。而且PSO-FCM算法在各年份数据上最小有效性函数值的平均值基本小于FCM算法,聚类效果更好。

将上述两种算法有效性函数值所对应的划分方式作为最终聚类结果,发现FCM和PSO-FCM对2010年、2011年、2014年、2015年、2016年和2017年的房价泡沫度、增长率和波动度的聚类结果基本一致,而2012、2013、2018年结果有一定差异(表2)。

表1 2018年我国35个大中城市房价泡沫数据标准化处理结果

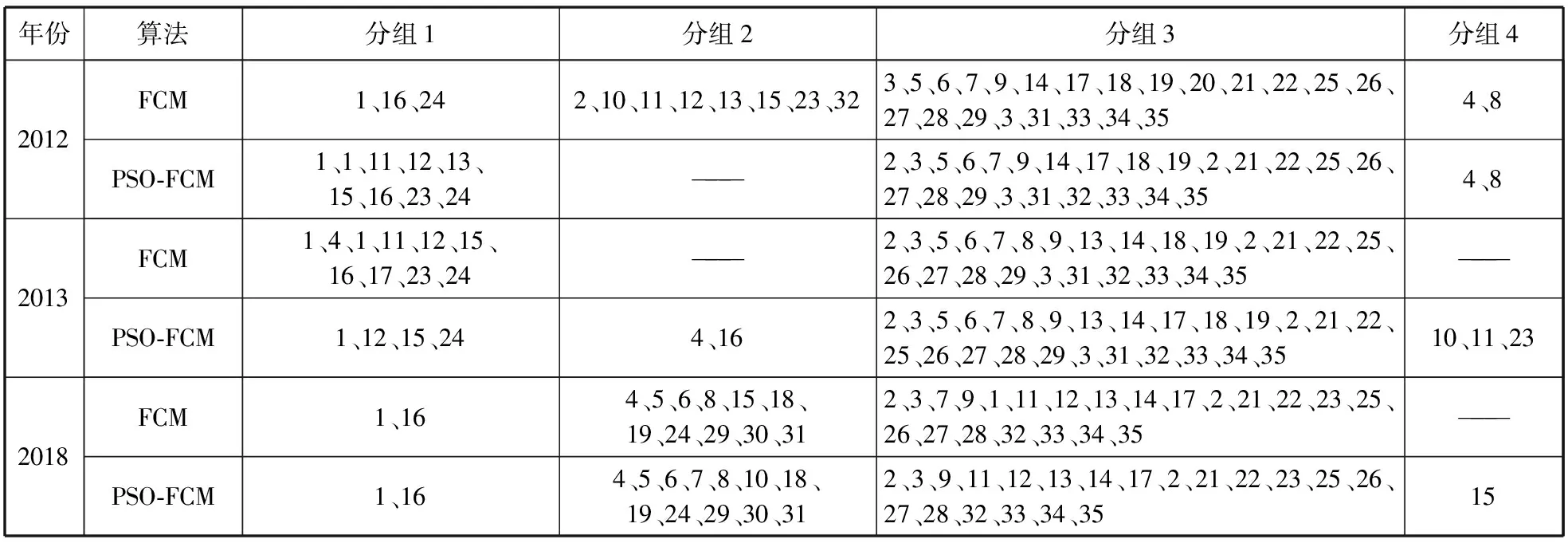
表2 FCM与PSO-FCM聚类结果的差异性对比

从泡沫度、增长率以及波动度上的数值特征来看(表3)，2012年用FCM算法确定最优聚类数目为4,组1和组3各维聚类特征的最大值和最小值差距较小,类内紧凑度较好,但多出的分组2类内差异较大,而与其他各类之间差异不明显,分类效果不及PSO-FCM算法;2013年两种算法聚类结果差异显著,FCM将北京、太原、上海、南京、杭州、福州、厦门、南昌等地分为分组1,类内差异较大,而PSO-FCM将波动度较大的太原和厦门两市单独分为分组2,将泡沫同比增长极快的上海、南京、广州三地单独分为分组4,相较FCM各类别间的特征更突出;2018年PSO-FCM将同比增长过快的福州单独分为分组4,且分组2、分组3相比FCM更为紧凑。综上可见，PSO-FCM算法更为合理。

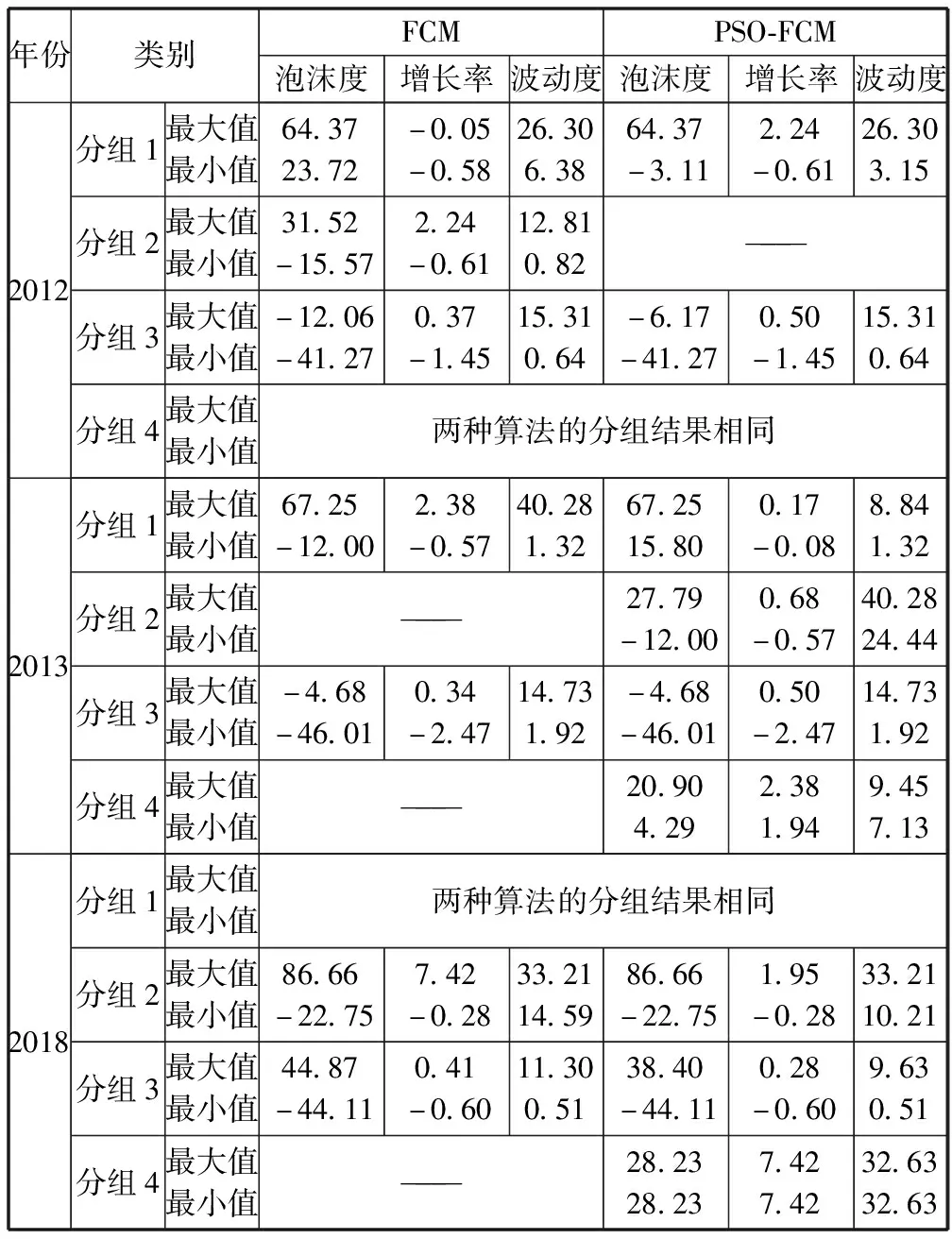
表3 FCM与PSO-FCM各类别的聚类维度特征

2.PSO-FCM算法下的房价泡沫聚类结果分析

表4 2010—2018各年度我国35个大中城市住房价格泡沫的聚类结果

根据聚类结果,可以将样本城市大致分为五种类型:双高型、可控型、波动型、潜在型和突变型(表5)。双高型城市的数量有所下降,主要为北京、上海、厦门、深圳这些一线城市,且北京、厦门近年泡沫增速明显放缓且波动逐渐变小,在2018年转换成可控型;而在2013年、2014年均为可控型的杭州和福州两市,房价泡沫历经几年波动后相继出现突变;波动型城市如太原、呼和浩特、沈阳、长春等虽然目前房价泡沫现象还不明显,但波动幅度较大,有可能会衍生出泡沫;大部分样本城市属于潜在型,其中哈尔滨、郑州、武汉、长沙、重庆、成都、兰州、西宁、银川、乌鲁木齐在研究期间一直保持泡沫度为负值且波动较小,而其余城市房价泡沫经过不断发展转化为其他类型;突变型城市房价泡沫极不稳定,泡沫度可能突然由低到高,如近几年天津、石家庄、太原、合肥等地房价泡沫从无到有,泡沫涨势较快,杭州、福州两地房价泡沫也相继再度膨胀,而海口虽然目前还未出现泡沫但泡沫度上涨很快。

表5 城市住房价格泡沫变化特征

三、结论与建议

本研究认为PSO-FCM方法数据容易获得,算法可行,可以用来进行房价泡沫聚类分析。研究尝试给出以下建议:(1)双高型城市如北京、上海、厦门、深圳泡沫度较高,虽然泡沫增速有所收窄,但波动仍然较大,需要稳步控制,逐步落实租售并举举措,控制投机需求,引导居住需求合理向租赁方式分流;(2)可控型城市虽然泡沫度较高,但泡沫增速放缓且波动较小,建议维持现有调控措施,防范后续泡沫进一步扩张的风险;(3)波动型城市如太原、呼和浩特、沈阳、大连、长春、济南、青岛、贵阳、昆明、西安虽然目前泡沫度较低,但近年泡沫波动较大,应加快建立和完善房地产业的泡沫预警制度,防范泡沫生成的风险;(4)潜在型城市如哈尔滨、南京、宁波、南昌、郑州、长沙等地,虽然目前泡沫度较低且波动较小,但对南京、宁波这些新一线城市仍应积极关注市场给予相应调控,防止后续市场出现大落的可能;(5)突变型城市如天津、石家庄、杭州、合肥、福州、海口近年泡沫同比增长极快,近几年泡沫度较高的天津、杭州、福州三市建议严格实施市场调控措施,防范投机行为,而对于目前泡沫度较低的石家庄、合肥、海口建议当地政府应适当调整住房用地的供应量,控制商品住房的不合理上涨。(6)部分城市如太原、长春、上海、南京、杭州、宁波、福州、厦门、深圳、海口等在不同泡沫类型之间转换较快,应注意建立住房市场长效调控机制。□