基于有时间约束的节约里程法对配送线路的优化

刘晓云

(天津工业大学 天津 300387)

近年来，线上、线下超市的增多、产品的多样化，随之带来的是竞争压力的增大，零售业对供应物流的要求也越来越高。而路径的优化，很好地解决了低库存和低运输成本之间的矛盾。而配送的运作模式是车辆根据事先的路线安排，从超市配送中心出发，前往多家连锁店进行配货，最后返回仓库。这样既能提高车辆装载量，又能保证产品的及时供给。不必等到库存严重不足时再进货，减少了为转载率而大量进货的高库存成本问题，同时给需求量较少的商家带来了便利，使其在最大程度上实现JIT供给。

一、节约里程法简述

(一)节约里程法基本原理。节约里程法的基本原理是几何学中三角形一边之长必定小于另外两边之和。运用到运输上来说就是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。

(二)节约里程法基本条件。节约里程法的运用必须要满足以下几个约束条件:(1)每个配送点只能由一辆车来完成配送服务,不可分批配送；(2)配送车辆的最大运载量是固定的,配送车辆不可以超载配送；(3)配送中心的货物是可以完全满足配送点的需求,不会出现短缺货物现象；(4)配送点的数量、配送点与配送中心的距离以及各配送点之间的距离都是已知不变；(5)满足用户到货时间要求。

二、建模背景

(一)研究内容。本文研究的主要内容可以分为三个方面：第一，通过情景假设对A连锁超市进行实际建模；第二，建立A连锁超市的目标函数，定义相关变量、约束条件，并用数学公结合超市现有的网点布局，将基于时间窗约束下的节约算法应用于各实际连锁超市的配送路径优化中,最终得出A连锁超市的配送路线优化方案。第三,对配送路径的优化方法做了归纳性论述，并详细论述了节约算法，并在此法的基础上做了有时间窗约束下的优化。

(二)研究意义。本文的研究意义在于：第一，运用节约里程法对A连锁超市配送路线进行优化，缩短不必要的配送路线，减少配送车辆的调用，降低配送成本，提高连锁企业市场的竞争力。第二，通过对A连锁超市的优化分析，可以将本方法推广到更多的物流配送生活实例中。

三、案例分析与实际建模

(一)模型假设。假设某地区共有5个连锁超市和一个生活用品配送中心。P0代表配送中心，P1…P5表示分别对应表示1…5连锁超市的位置。配送中心现在配有4t、6t、10t的货车，每辆车每次配送的距离被控制在160Km之内。假如车辆行驶时间和配送距离之间有正相关的关系，那么每辆车的均速就会保持在50Km/h。假设配送中心的配送活动从早上5点钟开始，那么配送量单位为t，装货的平均速度为0.5h/t；货车在预定时间内达到指定地点后停留一段时间，把货物卸下来。假如每小时可以卸下0.4t的货物，那么通过计算就能够得知每个运输车辆在不同超市的卸货时间。

(二)模型的建立与求解

1.确立目标函数

式中：dij,d代表超市i与超市j之间的距离，xijs=1或者0，1表示货车s从超市i到达超市j，0则代表货车s从超市j到达超市i；s代表发出车辆的次序；m代表配送中心配备的车辆数，m=4。

2.找出约束条件，根据A连锁超市的配送情况，确定约束条件为：

aj=1j-1+tj-1

Lj-1=aj-1+wj-1

gj≤aj≤hj

其中：Qs：第s辆车能承受的载重量；e：超市j需要配送的货物量。

(三)优化分析。第一步，将距离转变为时间；第二步，使用节约里程法算出各个分店间能省的距离数；第三步，把节约里程按照降序排序；排序处理后的结果见表1。

表1

第四步，按照节省距离排序表，装载量和时间窗的限制明确运输路线。

(1)第一条线路：P0→P3→P4→P0，可以派一辆最多可以载6t的货车载5.5t的货物，运行距离为159.1km，运行距离是小于160km的。

(2)第二条线路：P0→P1→P5→P0，可以派一辆最多可以载6t的货车载6t的货物，运行距离为24.4km，运行距离是小于160km的。

(3)第三条线路：P0→P2→P0，见图1。

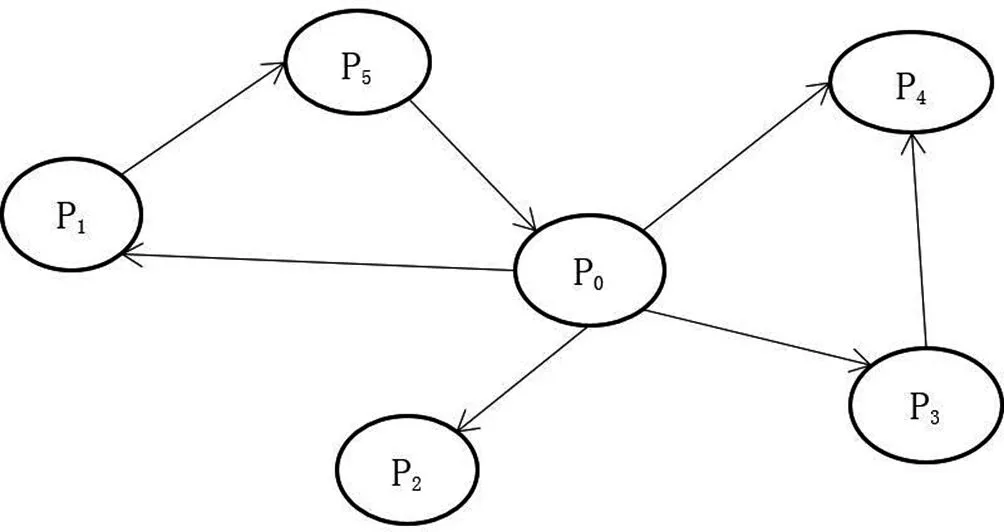
图1 A连锁超市优化配送路线图

(四)优化结果。在考虑到时间窗约束，和运行最大距离、最大载重量情况下，一共提出了三条配送路线，三条线路总行走距离187.5千米，必要车辆是4吨车，6吨车1台、10吨车1台，优化后方案节省了52.5千米。

四、结论

配送是仓库与门店的连接点,在超市运营中发挥着不可或缺的作用。本文从配送路程长短对超市成本影响角度出发，建立基于节约里程法的优化模型，最终较好地节约了超市的配送成本，为超市创造更好的经济收益。