基于COMSOL 的组合空腔结构声学覆盖层的声学性能分析

柯李菊，刘成洋，方智*

1 华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

2 中国舰船研究设计中心，湖北 武汉 430064

0 引 言

声学覆盖层是一种吸声能力很强的潜艇隐身结构，主要用于覆盖壳体，抑制壳体振动并吸收敌方主动声呐信号，降低潜艇的声反射强度，以减小被探测距离[1-3]。目前，声学覆盖层已经专用化，在潜艇壳体的特定区域或频段需要针对性地敷设不同种类的声学覆盖层，由此要求声学覆盖层的材料及内部声学结构的设计必须多样化。现有的含空腔声学覆盖层主要作为吸声结构，内部腔形结构多为简单且规则的形状（例如圆柱形、球形、锥形或者喇叭形），其与均匀无腔覆盖层相比，吸声效果较好[4]。含空腔声学覆盖层除具有良好的吸声性能外，还兼有一定的隔声性能。当将空腔结构引入隔声结构中时，与不含空腔结构的声学覆盖层相比，其隔声效果得到了较大改善，但仍存低频隔声效果不好且在静水压力下会产生较大变形等问题[5]。

在现有空腔谐振型声学覆盖层的专利和文献中，多数针对圆柱形和指数形空腔进行研究。刘国强等[6]使用COMSOL 有限元仿真软件计算了椭球形空腔声学覆盖层的吸声特性，分析了穿孔率、材料厚度以及材料参数对吸声性能的影响规律，指出空腔穿孔率越大，声学覆盖层的吸声性能或隔声性能越好，但耐压性能越差；声学覆盖层厚度越大，其吸声性能和隔声性能越好。周江龙等[7]使用COMSOL 软件对圆柱形空腔声学覆盖层隔声量进行了仿真计算，结果表明，在相同穿孔率下，较大直径的圆柱空腔隔声效果更好。张冲等[8]使用COMSOL软件计算了球形空腔声学覆盖层在静水压力下的吸声特性，指出随着静水压力的增大，声学覆盖层的吸声效果会变差。赵颖坤等[9]基于弹性体和黏弹性体的波传递理论，分析了水中蜂窝夹层结构的隔声性能，指出蜂窝夹层结构的隔声性能比打孔橡胶夹层结构和均质橡胶结构的性能要好。唐世灏等[10]采用有限元方法研究了蜂窝空腔覆盖层的隔声性能，分析了蜂窝结构的胞元壁厚度和夹角以及材料参数对隔声量的影响，指出胞元壁厚越小，即空腔占比越大，声学覆盖层的隔声效果越好。

继含单一形状的空腔（单腔结构 ）声学覆盖层后，组合形状的空腔（组合空腔结构）覆盖层概念被提出。商超等[4]基于有限元法研究了组合空腔结构的覆盖层吸声特性，结果表明，其吸声特性明显优于具有相同穿孔率的单腔结构。Zhong等[11]提出一种新型空腔结构的声学覆盖层，即倒锥形空腔结构，将其吸声系数曲线与等容圆柱体空腔结构的声学覆盖层的吸声系数进行了对比，发现该声学覆盖层在低于5 000 Hz 频率范围内的吸声性能得到了提高。然而，对于组合空腔结构的覆盖层在隔声性能方面的应用及其研究鲜见报道。目前对于含空腔结构的声学覆盖层的研究方法有2 种：一是对于黏弹性介质中波传播特性的解析法[12]，二是有限元法[13-15]。对于几何形状较复杂的声学结构，较难得到解析解，故多采用有限元方法进行研究。陶猛和卓琳凯[14]采用波导有限元方法分析了组合型圆台空腔吸声覆盖层的声学特性。陈文炯和刘书田[15]采用有限元法研究了空腔形状与声学性能参数之间的关系。

针对单腔结构在低频吸声性能较差且受压后变形较大的问题，本文拟提出一种圆台组合空腔结构，使用COMSOL 软件对其隔声、吸声和耐压性能进行仿真分析。首先，介绍使用COMSOL 软件建立组合空腔结构的声学覆盖层物理模型以及计算其隔声和吸声性能的方法，并将仿真结果与实验测量结果进行对比，以验证COMSOL 软件的适用性和准确性。然后，使用COMSOL 软件分析空腔几何尺寸对声学材料的隔声、吸声和耐压性能的影响，提出一种在圆台组合空腔四周均匀布置圆柱小孔的混合空腔结构，并仿真分析小孔尺寸对材料声学性能和耐压性能的影响规律。最后，对得到的规律进行总结，为声学覆盖层内空腔结构的设计提供理论依据。

1 物理模型与方法

1.1 隔声量和吸声系数的计算

由于空腔结构在声学覆盖层内周期性均匀分布，排列形式一般是四边形或三角形，因此采用周期性边界条件，可以只研究1 个单胞单元内的声波传播规律，来代替无限大声学覆盖层。为了便于研究，长方体或正棱柱体形成的单胞单元均可简化为圆柱体单元，对于轴对称的空腔结构，可以使用二维模型代替三维模型，进而降低计算成本。简化的声学覆盖层二维轴对称模型结构示意图如图1 所示。

本文主要研究组合空腔结构声学覆盖层的隔声和吸声性能。简化的圆台组合腔型声学覆盖层单胞二维有限元模型如图2 所示，采用COMSOL软件模拟水声管测量声学覆盖层的隔声量和吸声系数，在水听器1 处测得的声压为 p1，水听器2 处测得的声压为 p2，水听器3 处测得的声压为 pt。水听器1 与水听器2 之间的距离为d，根据国标GB/T 18 696.2—2002 规定，各水听器的位置均有相应的计算公式。采用声-弹性波交互物理场，将声学材料域设置为固体力学模块，而空腔内的空气域和水声管中的水域被设置为压力声学模块。在声波入射端施加平面波声源，在声波透射端添加完美匹配层（PML）边界条件，模拟无反射端边界条件。

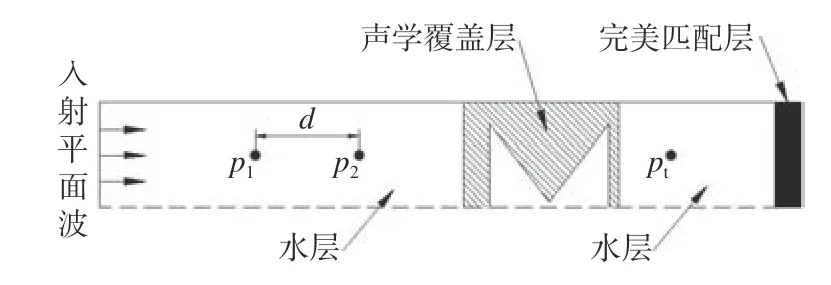
图2 简化的组合空腔结构声学覆盖层有限元模型Fig. 2 Simplified FE model of the anechoic layers with combined cavity structure

根据样品的声压反射系数 Rre，求得测试样品的吸声系数 α为

1.2 模型有效性验证

圆柱形空腔声学覆盖层的声学有限元分析技术比较成熟。为了验证本文中采用COMSOL 软件计算隔声量方法的有效性，参照文献[16-17]，选取厚度为40 mm 的带圆柱空腔的覆盖层结构，计算其隔声量曲线，并分别与文献[16]的仿真结果和文献[17] 的实验结果进行对比。圆柱空腔高为20 mm，直径为15 mm，覆盖层单胞模型直径为28.2 mm。隔声材料的物理参数为：杨氏模量E=1.8 MPa，泊松比 ν=0.499 76， 密度 ρ=1 000 kg/m3，损耗因子 η=0.15。提取水声管中3 个传声器位置的声压值 p1， p2和 pt，并根据传递函数法计算样品的隔声量。本文仿真计算结果与文献[16] 结果的对比如图3 所示。由图可见，本文计算值与文献[16]的结果吻合较好；与文献[17]实验结果的变化趋势相同，但数值存在一定的差异。其原因可能是实验测量过程中无反射端的设置与仿真计算中的设置不一致，也有可能是实验过程中存在水声管壁与隔声材料和水介质的耦合效应，而在仿真计算中未考虑此效应所致。而空腔型式的改变并未影响仿真计算方法的准确性，因此可以使用COMSOL 软件进一步仿真计算组合空腔结构声学覆盖层的隔声量。

图3 隔声量的有限元仿真结果与文献结果的对比Fig. 3 Results comparison between FE simulation and Reference[16-17] of sound transmission loss

为了验证采用COMSOL 软件计算吸声系数的有效性，选取厚度为30 mm 的均匀无腔覆盖层；隔声层为橡胶材料，参数与前文所述相同；钢背衬厚度为5 mm，材料物理参数为：杨氏模量E=2.07×105MPa，泊松比ν =0.3， 密度ρ =7 800 kg/m3。吸声系数的COMSOL 计算值与文献[18]的解析结果的对比如图4 所示。由图可见，两者结果吻合较好，验证了采用COMSOL 软件计算组合空腔结构声学覆盖层吸声系数的有效性。

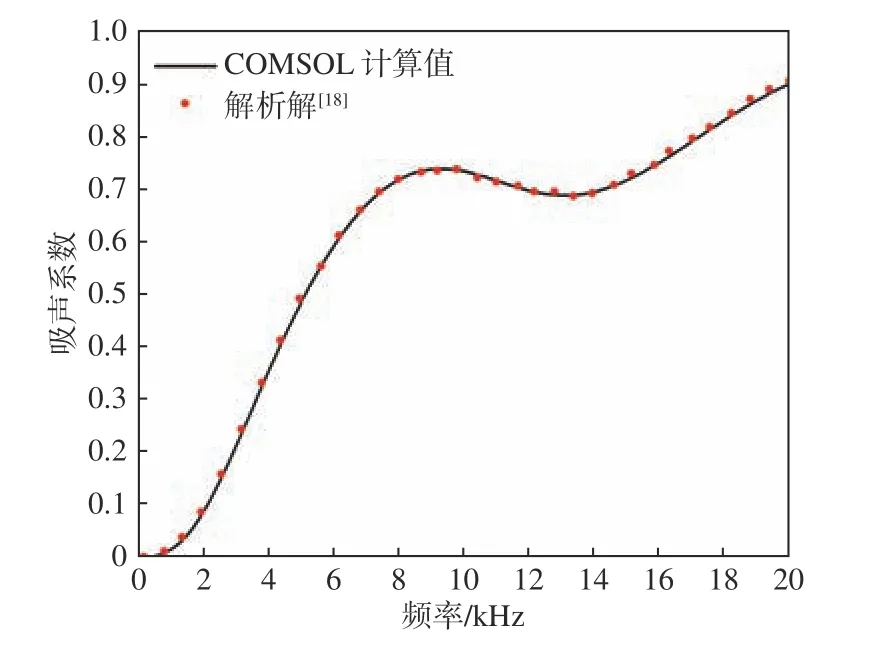
图4 吸声系数的有限元仿真结果与解析结果对比Fig. 4 Results comparison between FEM and analytical solution of the sound absorption coefficient

1.3 变形量的计算

在计算受压变形量时，同样利用COMSOL 软件进行建模，将声学覆盖层下端设置为固定边界，三维模型的周期性边界条件转化为二维轴对称模型的法向量位移为零的边界，覆盖层模型上端为载荷边界。本文采用模型最大压缩变形量来简单衡量声学覆盖层的耐压性能。

1.4 组合空腔结构与传统空腔结构对比

传统空腔结构主要包括球形、圆锥形、圆柱形等，本文研究的组合空腔由上、下圆台组成，结构示意图如图5 所示。为了体现组合空腔结构在隔声性能上的优越性，选取3 种穿孔率相同的空腔结构（圆柱形、球形和圆台组合型）计算其隔声量，计算结果对比如图6 所示。由图可见，组合空腔结构的隔声效果整体比传统空腔结构的隔声效果更好。

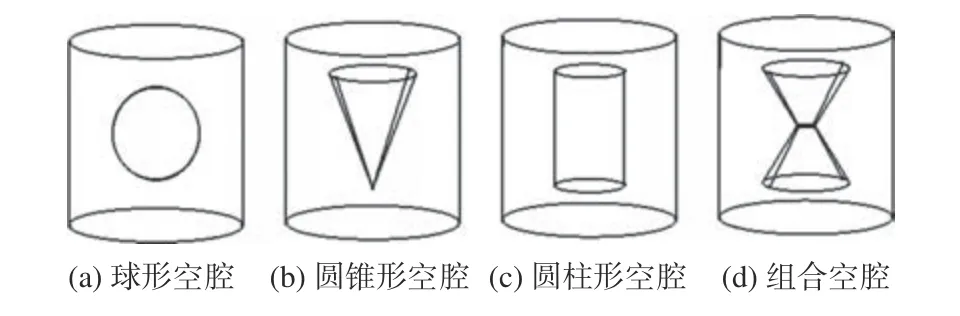
图5 传统空腔结构与组合空腔结构示意图Fig. 5 Schematic diagram of traditional cavity structures and combined cavity structures

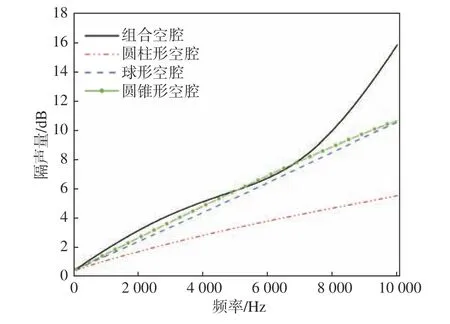
图6 不同空腔结构的隔声量Fig. 6 The sound transmission loss of different cavities structures

2 组合空腔结构几何尺寸对声学和耐压性能的影响

2.1 组合空腔结构大半径与单胞半径之比的影响

图7 组合空腔结构声学覆盖层有限元模型Fig. 7 FE model of anechoic layers with combined cavity structure

组合空腔结构声学覆盖层单胞有限元模型如图7 所示。由图可见，组合空腔结构由上、下2 个对称的圆台形空腔组成，图中阴影部分为橡胶域，空白部分为空气域。声学覆盖层厚度为30 mm，上、下各预留一定厚度的封孔层。声学覆盖层单胞半径为 R，上、下圆台空腔大半径分别为r1和 r2， 小半径为 r。上、下圆台空腔高度分别为h1= h2= 11.5 mm。保 持圆台小半径为 r=1 mm不变，改变隔声材料的单胞半径R 及圆台空腔大半径 r1和 r2，分析其对隔声量和吸声系数的影响。再取上、下圆台大半径相等，分别为r1=r2=6,7,8,9,10,11 mm，相应地声学覆盖层单胞半径分别取为R=7,8,9,10,11,12 mm。通过仿真计算分析组合圆台空腔大半径与声学覆盖层单胞半径之比不同时的隔声量、吸声系数及其在3 MPa 静水压力下的变形量，结果分别如图8～图10 所示。

图8 不同空腔大半径与单胞半径比下的隔声量Fig. 8 The sound transmission loss under different r1/R

图9 不同空腔大半径与单胞半径比下的吸声系数Fig. 9 The absorption coefficient under different r1/R

图10 不同r 1/R的组合空腔结构在3 MPa 静水压力下的变形量Fig. 10 Deformation of combined cavity structure with different r1/R under 3 MPa hydrostatic pressure

由图8～图10 可以看出，随着 r1/R的增大：1）组合空腔结构的整体隔声效果变好，并会逐渐出现隔声量峰值，且峰值频率向低频移动；2）吸声系数峰值频率向低频移动，中、高频的吸声效果变差。但 r1/R越大时，空腔穿孔率越大，组合空腔结构声学覆盖层的耐压性能越差，在3 MPa 静水压力下的变形量越大。

2.2 组合空腔结构大半径的影响

减小声学覆盖层的空腔穿孔率可以改善其耐压性能，但隔声性能会受影响。在固定声学覆盖层单胞体积的基础上，即保持R=11 mm，r=1 mm不变，改变组合圆台空腔大半径，分别取r1=r2=6,7,8,9,10,11 mm，分析声学覆盖层隔声和吸声性能的变化趋势，得到的隔声量变化曲线和吸声系数变化曲线如图11 和图12 所示。

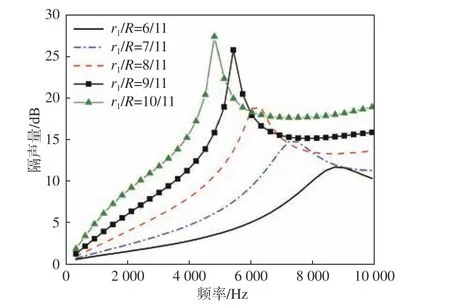
图11 组合空腔结构体积不同时的隔声量Fig. 11 The sound transmission loss with different volumes of the combined cavity structure

图12 组合空腔结构体积不同时的吸声系数Fig. 12 The absorption coefficient with different volumes of the combined cavity structure

由图中可以看出，当单胞体积固定时，增大圆台大半径r1，空腔体积变大，导致穿孔率增大，隔声量曲线和吸声系数曲线中的峰值频率都逐渐减小，峰值不断增大，整体隔声性能增强，但中高频的吸声性能变差。

2.3 单胞半径的影响

在固定空腔体积的基础上，即 r1=r2=10 mm，改变单胞半径，分别取 R=11,12,13,14,15 mm，分析声学覆盖层隔声和吸声性能的变化趋势。图13和图14 为改变单胞半径时的隔声量和吸声系数变化曲线。

图13 不同单胞半径时的隔声量Fig. 13 The sound transmission loss with different unit cell radii

图14 不同单胞半径时的吸声系数Fig. 14 The absorption coefficient with different unit cell radii

由图可以看出，当空腔体积固定时，增大单胞体积，即空腔体积占比减小时，隔声量曲线中的峰值会向高频移动，峰值增大，中、高频范围内的隔声性能改善；吸声系数曲线中的峰值频率也朝高频移动，峰值基本不变，中、高频范围的吸声性能也得到改善。

2.4 圆台不对称性的影响

分析组合空腔结构中上、下圆台不对称时的声学覆盖层声学性能和耐压性能的变化规律。固定空腔下圆台大半径 r2=10 mm，上圆台大半径分别取 r1=6,7,8,9,10 mm时，仿真计算的隔声量曲线和吸声系数曲线分别如图15 和图16 所示。再固定上圆台大半径为 r1=10 mm，下圆台大半径r2=6,7,8,9,10 mm时，仿真计算得到的声学性能曲线如图17 和图18 所示。分别改变上、下圆台大半径时，声学覆盖层在3 MPa 静水压力下的变形量如图19 所示。

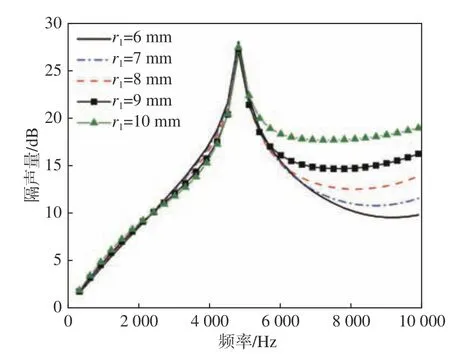
图15 改变上圆台大半径 r1时的隔声量Fig. 15 The sound transmission loss with different r1

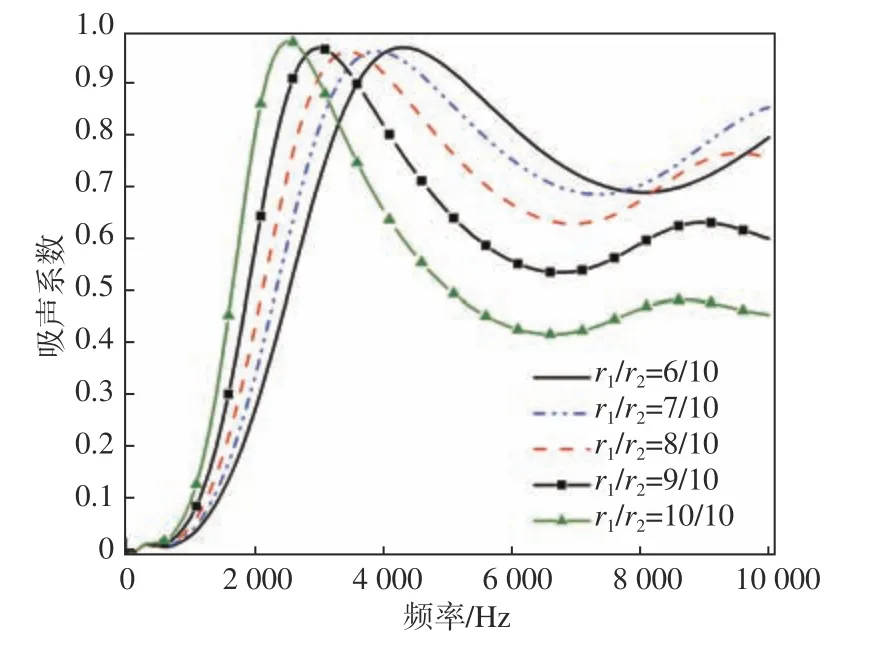
图16 改变上圆台大半径 r1时的吸声系数Fig. 16 The absorption coefficient with different r1

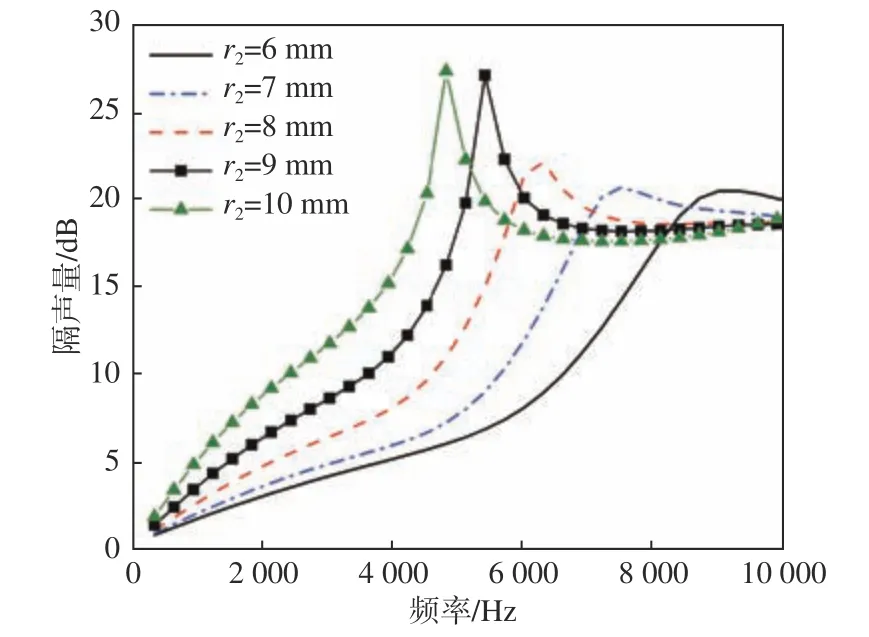
图17 改变下圆台大半径 r2时的隔声量Fig. 17 The sound transmission loss with different r2

图18 改变下圆台大半径 r2时的吸声系数Fig. 18 The absorption coefficient with different r2

图19 分别改变上、下圆台大半径时声学覆盖层在3 MPa 静水压力下的变形量Fig. 19 Deformation of anechoic layers with different r1 and r2 under 3 MPa hydrostatic pressure

由图15～图16 可以看出，当 r2固 定时， r1越大，中、高频段的隔声性能越好，隔声量曲线的峰值频率、峰值和低频段隔声量均没有太大的变化。但随着 r1的增大，吸声系数峰值频率逐渐朝低频移动，中、高频吸声性能变差。

由图17～图18 可见，当 r1固 定时， r2增大，隔声量曲线中出现明显峰值；且 r2越大时，峰值频率不断减小，峰值不断增大，但吸声性能没有明显变化。这说明，靠近声波入射端的空腔开口尺寸对隔声量曲线中峰值频率以及低于峰值频率范围内的隔声性能影响很小，隔声量的峰值频率和峰值更多地取决于远离入射端的圆台空腔的大半径r2， 且 r2越大，峰值频率越小，峰值越大，声学覆盖层在中、低频的隔声性能越好。而靠近入射端的空腔开口对吸声性能的影响更大，开口越大，峰值频率越小，远离入射端的开口对吸声性能的影响则不明显。

由图19 可以看出，随着空腔体积的增大，声学覆盖层在3 MPa 静水压力下的变形量增大，且r1对 结构耐压性能的影响比 r2的大。这表明，靠近受压面的一端开口越大，结构的耐压性能越差。在保证声学覆盖层的隔声性能的基础上，可以增大远离声波入射一侧的空腔体积而减小靠近声波入射一侧的空腔体积，进而提高其耐压性能。

3 圆柱小孔对声学性能和耐压性的影响

由前述分析可知，穿孔率越大，声学覆盖层的隔声性能越好，但耐压性能越差。因此，组合空腔结构的设计应兼顾隔声性能和耐压性能，根据需改善的频率范围合理设计组合空腔体积和空腔间距（即单胞的体积）。为了平衡空腔结构的隔声性能和耐压性能，研究在前文的组合空腔结构周围增加1 组圆柱小孔时对声学覆盖层的隔声、吸声性能和耐压性能的影响。

3.1 有/无圆柱小孔的影响

图20 为在前文的组合空腔结构四周增加圆柱小孔后的声学覆盖层结构示意图。小孔沿圆周分布，相邻两孔夹角为45°，小孔半径为 r0=1 mm，高度为 h=3.5 mm，小孔距组合空腔中心线的距离为10 mm。声学覆盖层单胞体积和组合空腔结构的体积均不变，分别计算添加圆柱小孔前、后组合空腔声学覆盖层的隔声和吸声性能，2 种结构的隔声量和吸声系数比较曲线如图21 和图22所示。

图20 四周增加圆柱小孔后的声学覆盖层结构示意图Fig. 20 Schematic diagram of structure of anechoic layers adding cylindrical holes around

图21 有/无圆柱小孔的组合空腔结构隔声量对比Fig. 21 Comparison of sound transmission loss related to combined cavity structures with/without cylindrical holes

图22 有/无圆柱小孔的组合空腔结构吸声系数对比Fig. 22 Comparison of absorption coefficient of combined cavity structures with/without cylindrical holes

由图可知，在固定声学覆盖层单胞体积和组合空腔体积的前提下，在原组合空腔四周增加一定数量的圆柱小孔能提高覆盖层在低频段的隔声和吸声性能，并且会使得峰值频率向低频移动，相较而言对隔声性能的影响更为明显。这是因为圆柱小孔增大了声学覆盖层中空腔的有效体积，尤其在远离声波入射方向的一侧，即图19 中的下圆台大截面一侧，圆柱小孔增大了下圆台空腔的大半径，进而使得隔声量中的峰值频率向低频移动，且在低于峰值频率范围内的隔声性能变好。

3.2 圆柱小孔的高度和孔径的影响

圆柱小孔个数固定为8 个，均匀分布，结构示意图如图20 所示。改变圆柱小孔的高度和孔径，分析其对声学覆盖层的隔声、吸声性能和耐压性能的影响，计算结果分别如图23～图26 所示。

图23 圆柱小孔的高度对隔声量和耐压性能的影响Fig. 23 Influence of the height of cylindrical holes on sound transmission loss and pressure resistance

图24 圆柱小孔的高度对吸声系数的影响Fig. 24 Influence of the height of cylindrical holes on absorption coefficient

图25 圆柱小孔的半径对隔声量和耐压性能的影响Fig. 25 Influence of the radius of cylindrical holes on sound transmission loss and pressure resistance

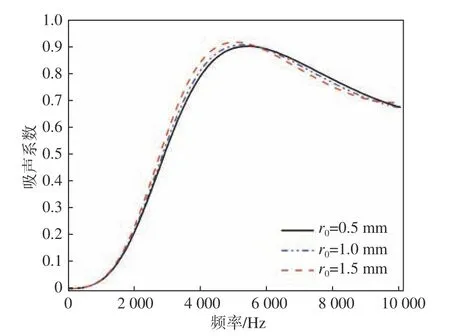
图26 圆柱小孔的半径对吸声系数的影响Fig. 26 Influence of the radius of cylindrical holes on absorption coefficient

由图可知，当圆柱小孔的半径固定时，圆柱小孔的高度对隔声和吸声性能的影响均不大，对峰值之前的隔声性能基本没有影响。当圆柱小孔的高度固定时，圆柱小孔半径增大，导致空腔的有效体积增加，因此隔声性能在低频段略有提升，隔声量和吸声系数的峰值频率朝低频移动少许。而圆柱小孔的半径和高度变化时，声学覆盖层的最大变形量变化均不大，这说明圆柱小孔的体积变化对声学覆盖层的耐压性能影响很小。

4 结 论

针对目前单一腔型声学覆盖层低频隔声性能以及耐压性能较差的情况，本文采用COMSOL 有限元软件建立圆柱空腔声学覆盖层的分析模型，通过与实验测量结果对比，验证了有限元分析方法的有效性，进而计算对比了组合空腔不同几何尺寸下声学覆盖层的隔声量、吸声系数及其在3 MPa 静水压力下的最大变形量。得出以下结论：

1） 当组合空腔结构为上、下对称结构和声学覆盖层单胞体积固定时，空腔部分圆台的大截面面积越大，即穿孔率越大，隔声量和吸声系数中的峰值频率越向低频移动，且低频段的隔声效果更好；当组合空腔结构的体积固定时，随着声学覆盖层单胞体积的增大，即穿孔率降低，隔声量和吸声系数中的峰值频率略微向高频移动，中、高频的隔声量增大。

2） 当组合空腔中的上、下圆台结构为非对称结构时，声学覆盖层的隔声性能更多地取决于远离声波入射端的圆台大半径，吸声性能主要取决于靠近声波入射端的圆台大半径，而靠近受压一侧的圆台大半径同样对声学覆盖层的耐压性能影响较大。

3） 在声学覆盖层单胞体积和空腔体积固定时，组合空腔四周布置一定数量的孔径较小的圆孔，会提高声学覆盖层在低频段的隔声和吸声性能，并且会使峰值频率向低频移动。小孔的高度和孔径变化对隔声和吸声效果的影响不大。