最小二乘法在洞头区极大风速订正预报中的应用*

武丰民 吴舒婷

(1.浙江省气象科学研究所,浙江 杭州 310008;2.温州市洞头区气象局,浙江 温州 325700)

0 引 言

目前，准确的近地面风速预报对生产生活越发重要，尤其在海上航行、重大活动以及风力发电中，风速预报都发挥着关键作用。以洞头区为例，当极大风达到7级以上时，部分船只需要停航。因此精确的风速预报对该地区的岛际交通有很大影响。

风速预报主要有动力和统计两种方法[1]。动力方法也称物理方法，一般指数值预报或者利用动力模块对数值产品进行解释应用。由于近地面风场不仅受大尺度环流影响，而且对地表高程和地表粗糙度等因素也非常敏感，一般中尺度模式的风速预报往往存在较大误差[2]。即使是利用诊断模块对模式产品进行动力降尺度，在初始场质量较差的情况下，也很难得到满意的结果。统计方法包括传统统计[3-4]和机器学习[5]等方法，主要根据历史数据之间的统计规律对预报产品进行订正，该方法可以有效减小模式的系统误差，对一些模式无法直接预报的要素(如极大风速)，也可以通过统计拟合得到。

最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配，是最常用的曲线拟合方法。利用最小二乘法可以简便地求得未知数据，并使得这些数据与实际数据之间误差的平方和为最小。由于最小二乘法一般是针对站点建立模型，那么订正模型在不同站点的表现如何，建立一个稳定的模型需要多少样本，将不同风速的样本进行分段建模是否比将所有样本直接建模具有更好的效果？这些是在进行最小二乘拟合试验时必须考虑的问题。本文以洞头区极大风速为例，利用最小二乘法对浙江快速更新同化系统生成的模式预报结果进行订正试验，检验最小二乘法在该地区的使用效果，并试验了样本长度和分段建模对结果的影响。该研究对最小二乘法在风速订正中的应用具有一定参考意义。

1 资料和方法

本文研究区域为27.6°～28.1°N、120.8°～121.4°E，包含了温州市洞头区及其周边部分区域。观测数据来自该区域内37个自动站的逐小时极大风资料。对观测数据做简单质量控制，主要是去掉缺测和风速为0的站点。

本文的数值模式资料采用了浙江快速更新同化系统(Zhejiang WRF-ADAS Rapid Refresh System，ZJWARRS)的风场预报结果。该系统用ADAS系统同化了探空观测和地面气象站等观测资料，提供高质量的预报初始场，并用WRF模式向前积分进行预报，每次预报24 h。WRF模式选用双重嵌套方案，大区域和小区域的水平分辨率分别为9 km和3 km[6]。本文所用的结果为3 km分辨率的预报结果，下文将该结果简称为ZJWARRS结果。

利用2018年12月到2019年6月共7个月的历史资料进行最小二乘拟合，模式资料选取08时起报、12 h预报时效的ZJWARRS结果，观测资料则利用相应时刻的极大风资料，针对37个站点、12个预报时效建立37×12个统计模型。

最小二乘拟合采用NCL软件中的函数(http://www.ncl.ucar.edu/Document/Functions/Built-in/lspoly.shtml)，权重系数设为1，即所有样本的权重相同。返回参数的个数设为3，即拟合方程为2次函数。假设x为ZJWARRS结果，y为观测结果，则拟合系数C=lspoly(x,y,1,3)。得到拟合系数后，利用该系数对2019年7—9月共3个月的ZJWARRS结果进行订正：

Y订正=C(0)+C(1)×x+C(2)×x2

2 结 果

2.1 最小二乘建模的效果

图1显示了ZJWARRS预报与最小二乘拟合的风速散点分布，横坐标为观测，纵坐标则为ZJWARRS(图1a)或拟合值(图1b)，实线代表观测与预报相等，散点在实线上方代表预报结果比观测大，反之则代表预报比观测小。由图1a可以看出，大部分ZJWARRS预报结果都比观测偏小，尤其在观测风速为5～20 m/s时，偏小最为明显。而经过最小二乘拟合(图1b)，这一负偏差可以得到有效纠正。

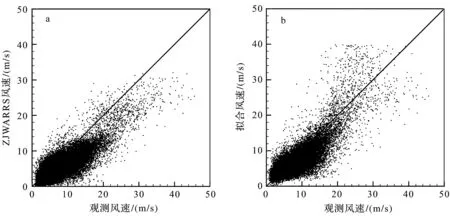
(横坐标为观测的极大风，纵坐标为ZJWARRS和拟合的风速，实线表示观测与预报结果相等)图1 ZJWARRS(a)、拟合(b)风速与观测结果的散点分布

ZJWARRS风速误差与风速的相关系数高达0.85(200个样本)，远超99%的显著性水平。也就是说，风速越大，预报的误差也会越大，反之亦然。为了分别检验不同风速条件下最小二乘拟合的效果，按观测风速将评估站次分成小于5 m/s、5～15 m/s、大于15 m/s 3档。由表1可以看出，风速为5～15 m/s时，改进幅度最大，约21%。值得注意的是，在评估的3个月时间内，5～15 m/s的极大风速约占70%比例，而小于5 m/s和大于15 m/s的风速比例只占30%。虽然最小二乘法对小于5 m/s的弱风改进不大，但由于弱风本身误差较小，对生产生活的影响不大。对业务中最为关注的大于5 m/s的极大风，最小二乘拟合的改进效果明显。

图2显示了3档风速条件下，最小二乘拟合对ZJWARRS改进的空间分布。与表1的统计结果一致，风速为5～15 m/s时，37个站中有27个站都有明显改进。对小于5 m/s和大于15 m/s的风，虽然有一些站点有明显改进，但也有相当一部分站点订正后比ZJWARRS预报结果更差。从空间分布来看，位于或者临近陆地的站点，如图2中标注的1-7站，由于本身风速较小，大风的样本少，在风速较小时有明显改进，而在风速偏大时，订正结果反而比ZJWARRS更差；相反，远离大陆的站点，如图2中的8-12站，本身的风速较大，虽在风速较小时订正效果不佳，但在风速较大时，改进非常显著。

表1 不同风速情况下ZJWARRS与拟合风速的均方根误差对比

((a)、(b)、(c)分别为在小于5 m/s、5～15 m/s、大于15 m/s情况下的统计。改进幅度的计算方法为图中的数字标记了12个观测站的位置)图2 3档风速下拟合结果对ZJWARRS预报改进的空间分布

通过以上分析可知，最小二乘拟合对风速的订正效果在不同站点上具有显著差别。为了进一步研究不同站点订正效果差别的原因，分别选取了订正效果最差和最好的3个站进行分析。如图3所示，3个效果差的站点风速均偏小，平均风速在5.5～7.5 m/s之间，而3个效果最好的站风速较大，平均极大风都在10 m/s以上。风速偏小时，ZJWARRS本身的误差较小，且ZJWARRS预报与观测之间的规律并不显著，使得订正改进的空间不大。而3个订正效果最好的站，平均风速大，ZJWARRS误差也大，预报结果普遍小于观测，且二者之间存在显著的线性规律，这种情况下最小二乘拟合的改进幅度都在30%左右。此外，3个订正效果最差的站都在图2中标记的临近大陆的7个站中，而3个订正效果最好的站则都在远离陆地的5个站中产生，这也与上文分析一致，即对平均风速大、ZJWARRS误差较大的站点，最小二乘拟合容易取得较好的效果。

(横坐标为观测，纵坐标为ZJWARRS预报，图中标记的站号对应图2中站点的位置，AVG代表该站参与建模所有样本的平均观测风速，百分数为针对ZJWARRS预报值订正结果的改进幅度，计算方法同图2)图3 改进效果最差(a—c)和最好(d—f)的6个站点观测与ZJWARRS预报的散点分布

2.2 样本长度的影响

一般而言，统计建模方法对样本数量较为敏感。在本次最小二乘拟合试验中，多少样本才可以建立起较为稳定的模型，样本数量对拟合效果又有怎样的影响？为了回答这一问题，设计了20组不同样本数量的拟合试验进行分析。设置一个首项为0、公差为10的等差数列，产生20组试验的样本数量。建模样本在上文中指出的2018年12月到2019年6月共7个月的历史资料中产生，为避免季节特征的影响，建模时采用随机选择样本的方法，根据数量不同选出20组数据分别建模。检验则依然采用2019年7—9月共3个月的数据。

试验结果如图4所示，图4a显示了不同样本数量建模对整体均方根误差的影响。可以看出，建模样本为10个时，拟合效果明显差于ZJWARRS结果。样本数量增加到20个时，误差比10个样本的建模结果急剧减小，比ZJWARRS也有明显改进。20个样本后，增加样本数量对建模效果的影响逐渐减小，尤其是在60个样本以后，再增加样本对模型的改进效果非常微弱。将风速分成3档进行统计，如图4b—4d所示，结果与不分档类似，都是在样本由10个增加到20个时改进幅度最大，而在样本数量达到60个左右时，拟合效果趋于稳定。

也就是说，20个样本是最小二乘拟合具有正效应的最低样本数，而60个样本已经使拟合的效果趋于稳定，再增加样本对拟合效果的改善并不明显。

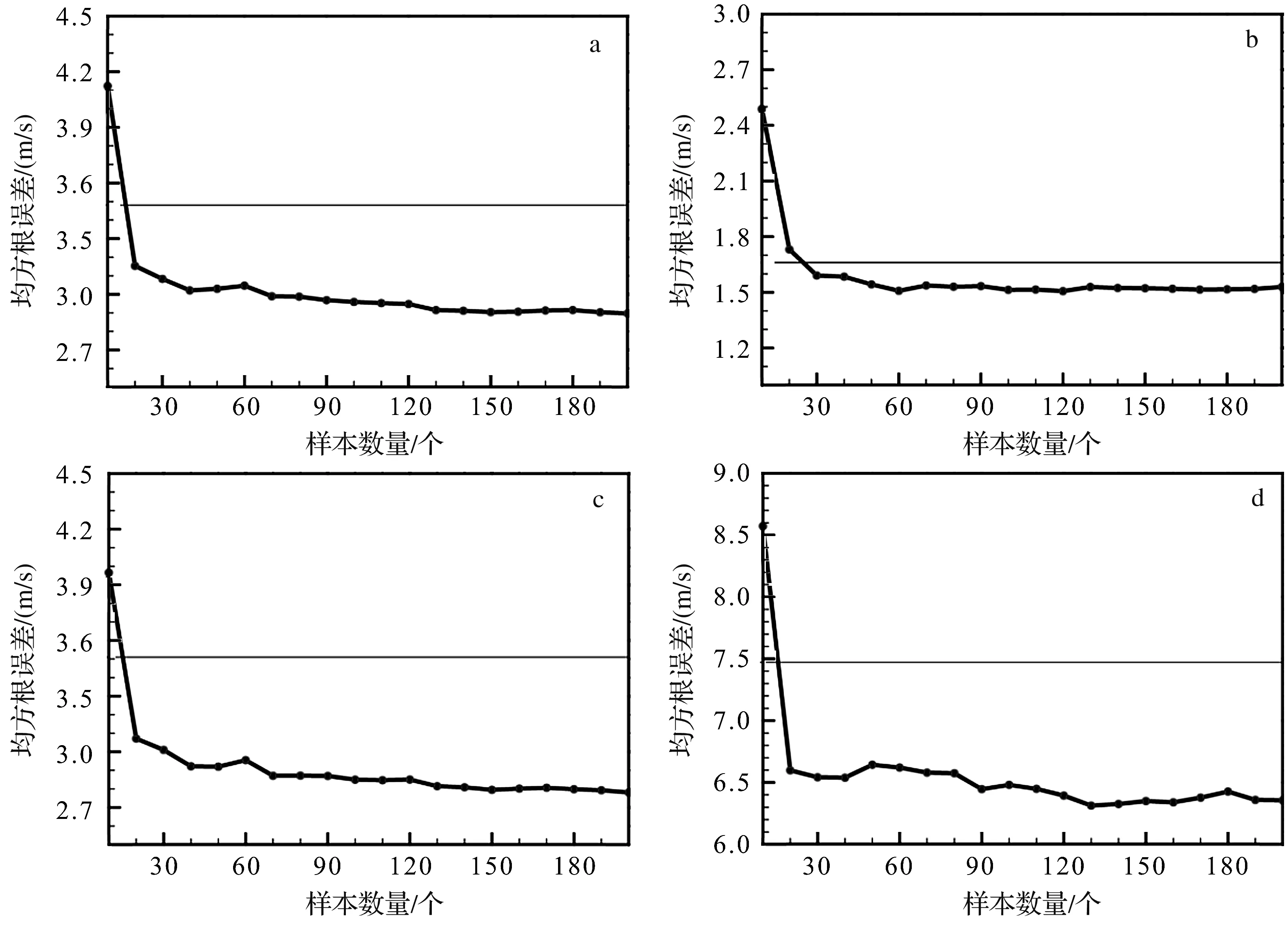
(横坐标为建模的样本数量，纵坐标为订正结果的均方根误差，横线为ZJWARRS预报的均方根误差。(a)为所有样本的统计;(b)、(c)、(d)分别针对小于5 m/s、5～15 m/s、大于15 m/s的样本统计结果)图4 建模样本长度对拟合效果的影响

2.3 分级建模的影响

由2.1节的分析可知，最小二乘法对风速较大的站点订正效果较好，而对风速较小的站点订正效果较差。这可能是由于对风速较大的站点建模时，大风速的样本较多，建立的模型更倾向于对大风速样本进行订正。由于最小二乘法中每个样本的权重相同，如果样本包含的风速跨度较大，模型要兼顾各个样本误差。若将不同风速的样本分开，单独进行拟合，是否能有效改进拟合的效果呢？

设计一组简单的试验来验证这一猜想。依然选择200个样本进行建模，但在建模时根据ZJWARRS预报风速大小将样本分成两组：小于10 m/s和大于10 m/s，当固定时效、固定站点上大于10 m/s的样本大于20个时，将该时效和站点的模型分成两种情况分别进行拟合；反之如果大于10 m/s的样本过少则依然将所有样本统一进行建模。进行检验时，根据ZJWARRS风速分别选择相应的模型进行订正。将此分级建模的结果与上文中不分级建模的效果进行对比，以验证样本分级对建模效果的影响。

检验结果如图5所示，可以看出在不同风速下，分级建模的表现差别较大。在风速小于5 m/s时，有8个站点比不分级建模有小幅改进，剩下的29个站拟合效果与不分级建模基本相当；当风速在5～15 m/s时，分级建模变差的站点有4个，其余33个站点与不分级建模效果相当；而在大于15 m/s风速情况下，虽然有8个站点比不分级有所改进，但同时有16个站点的效果变差。综合来看，分级与不分级的建模效果基本相当，并没有明显改进拟合结果。将风速分级的标准由10 m/s调整为8.6 m/s等，得到的结果与上述结果基本一致。

((a)、(b)、(c)分别为在小于5 m/s、5～15 m/s、大于15 m/s情况下的统计。改进幅度为图5 3档风速下分级建模对不分级建模结果改进的空间分布

3 结 语

本文利用ZJWARRS预报结果与极大风观测资料，对洞头区的37个站点进行最小二乘拟合试验，并利用3个月的资料对拟合结果进行了检验，同时还试验了样本数量和分级建模对拟合效果的影响，主要结论如下。

1)最小二乘拟合对ZJWARRS的风速预报具有一定的订正效果，尤其在风速为5～15 m/s时，订正结果的改进幅度约为20%。在空间分布方面，在离陆地较远、风速较大的站点，拟合效果最好，改进幅度在30%以上，而对风速较小的站点，订正有负效果。

2)20个样本是拟合具有正效应的最低样本数，随着样本增加，订正效果有所改进，但改进幅度逐步减小。当样本数量达到60个时，订正效果基本稳定，再增加样本数量对模型的改善效果有限。

3)简单将建模样本进行风速分级后分别进行建模，与不分级直接建模的效果相比，并没有明显优势。

最小二乘法是一种最简单的拟合统计方法，对ZJWARRS预报误差较大且具有一定规律的站点有一定的订正效果，但在不同站点订正效果差别较大。当样本数量达到一定程度后，再增加样本或者对样本进行风速分级建模都无法显著提高拟合的效果。在最小二乘法中所有样本的权重相等，故对样本中的异常值比较敏感。为了取得更好的订正效果，尝试考虑更多影响因子的统计方法以及动力模块的地形适应都是十分必要的。