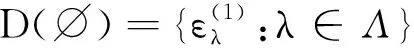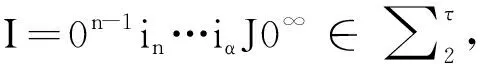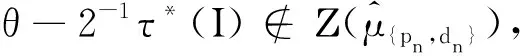一类Cantor-Moran谱测度的极大正交集

殷峰丽，白 梅

(周口师范学院数学与统计学院，河南 周口 466001)

对于一个具有紧支撑的Borel概率测度μ，若存在指数函数族E(Λ):={e2πiλx:λ∈Λ} (Λ为中的可数子集)为Hilbert空间L2(μ)的正交基，则称μ为谱测度，称Λ为谱测度μ的谱.关于谱测度理论的研究已经有很长的历史，可以追溯到1967年 Landau[1]的著名工作.自1974年Fuglede[2]提出著名的谱集猜想后，此理论获得广泛关注并取得了丰硕成果[3-10].经过近半个世纪的蓬勃发展，目前依然是傅里叶分析及其应用中的研究热点之一．

由于不同的谱对应的傅里叶级数的收敛性未必相同，为了更好的研究收敛性，有必要寻找更多的谱，而寻找更多谱的渠道之一是完全刻画极大正交集.Dutkay等[11]于2009年刻画了四分康托测度的所有极大正交集，他们是借助4进制展式以及二分树上的谱标签进行刻画的.2013年，戴欣荣等[12]考虑了连续型数字集所诱导的自相似测度，他们利用q分树上的极大映射对极大正交集Λ进行分类.受这些思想的启发，本文关注一类Cantor-Moran测度[13-14]，考虑给出其极大正交集的刻画.Cantor-Moran测度的具体构造如下：

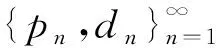
是一个由无穷个离散测度卷积生成的Borel概率测度，称其为Cantor-Moran测度，这里δE=(#E)-1∑e∈Eδe，#E表示集合E的势．

1预备知识及主要结论

1)E(Λ)中任意元素两两正交；

2) 若α∉Λ，eα不与eλ正交 (λ∈Λ).

给定测度μ，其傅里叶变换为

对于测度μ{pn，dn}，通过计算可得其傅里叶变换为

这里，Mdn(ξ)=e-πidnξcos(πdnξ)，Pn=p1…pn.令Ζ(h)={ξ:h(ξ)=0}，则

且

(1)

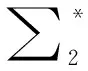
i)τ(∅)=τ(0n)=0，n≥1;

ii) 对任意k≥1，τ(i1i2…ik)∈(ik+2

给定一个极大映射τ，定义如下集合

及

定理1Λ(0∈Λ)是L2(μ{pn，dn})的极大正交集当且仅当存在极大映射τ使得

2主要结论的证明

本节给出定理1的证明，为此首先给出一个引理.为了行文的完整性，详述如下.

引理1[15]令Ck={-1，0，1，…，bk-2}，其中整数bk≥3(k≥1)，则对任意n∈，n≠0，存在唯一的σ=σ1σ2…σk(σk∈Ck，σk≠0)，使得

n=σ1+σ2b1+…+σkb1b2…bk-1∶=π(σ).

此外，若n=0，则σ=σ1=0．

证明对任意n∈及|n|

则n=π(σ).当|n|>b1时，则n可以被唯一的分解为n=c1+n1b1，这里c1∈C1.若|n1|

注此引理说明了任意整数按照此种方式展开，展式是唯一的，由于展开式中每层的系数属于不同的数集，因此此种展式也称整数n依Moran进制C1×C2×…展开．

k∈，m∈2

其中a0=0. 由引理1将aλ依Moran进制C1×C2×…展开，则有

(2)

为前n项系数确定的Λ中所有元素依(2)展开式第n+1项系数的全体，其中ci∈C1，1≤i≤n. 有如下引理．

引理2设0∈Λ⊂. 若Λ是L2(μ{pn，dn})的极大正交集，则D(∅)仅含有两个奇偶性不同的元素. 进一步，若D(c1，c2，…，cn)(cj∈Cj)非空，则它也仅含有奇偶性不同的两个元素. 特别地，0∈D(0，…，0)．

证明显然0∈D(∅)，0∈D(0，…，0). 若D(∅)只含有一个元素，则D(∅)={0}. 取C1中奇数α，则对任何λ∈Λ，由公式(2)可得

下面用归纳法证明所得结论. 假设上述情况对n-1成立. 若D(c1，c2，…，cn)非空，则所有D(c1，c2，…，ck)(k≤n)也非空. 可以说明D(c1，c2，…，cn)必定含有至少两个元素. 否则，考虑

这里α∈Cn+1且与D(c1，c2，…，cn)中元素奇偶性不同. 断言θ与Λ中所有元素都正交. 事实上，若λ∈Λ，则λ可表为

令k为满足Ι|k≠Ι′|k的第一个指标. 由于dn+1|dn，故

下证必要性. 定义τ(∅)=0且二分树的第一层各分支τ(i1)对应D(∅)中与i1共奇偶的数. 对于I=i1i2…in，定义τ(Iin+1)对应D(τ(I|1)，…，τ(I|n))中与in+1共奇偶的数. 由归纳法和引理2知，τ是定义好的，且对任意k≥1有τ(0k)=0.