动手“做”数学，活动“启”思维

丁月芳

【摘要】“我听说了，就忘了;我看见了，就领会了;我做过了，就理解了。”这句名言突出了“做”的重要性，深刻地揭示了“探求的意义在于经历”。真正意义上的“数学活动”是引导学生“做”数学，让学生借助有实际意义的工具为中介的“做”来获得知识。通过动手“做”，让学生经历真实的探究过程、合作与问题解决，促进数学素养的课堂落地。本文以《圆柱和圆锥》动手“做”活动为例，阐述动手“做”数学活动的实践与思考。

【关键词】动手“做”数学   数学思维   核心素养

六年级下册《圆柱和圆锥》这一单元知识间的关联较复杂，计算也较烦琐，学生有一定的畏学情绪。如何才能使这部分内容变得让学生触手可及，让学生体验探索的乐趣？教师可以指导学生通过动手“做”，使其经历真实的探究过程、合作与问题解决，发展学生的核心素养。

一、资源整合——基于动手“做”活动的素材重组

新一轮课改倡导自主、合作、探究的学习方式。我们的教学不能简单地告诉学生结果，也不是那种浅层次的探究，而是要通过对单元的整体设计，鼓励学生参与到深度学习之中，在探究中，积累学习方法和经验，更重要的是让学生通过学习经验的不断积累，学习如何把握共性，分辨差异。下面以3道习题为例：

（1）教材第22页第6题：

（2）教材第25页第5题：

一块圆柱形橡皮泥，底面积是15平方厘米，高是6厘米。

？譹？訛把它捏成底面积是15平方厘米的圆锥形，高是多少厘米？

？譺？訛把它捏成高是6厘米的圆锥形，底面积是多少平方厘米？

（3）教材第23页思考题：

一个圆锥和一个圆柱底面积相等，体积的比是1∶6。如果圆锥的高是4.2厘米，圆柱的高是多少厘米？如果圆柱的高是4.2厘米，圆锥的高是多少厘米？

立足单元整体设计来看，以上3道习题，落脚点都是围绕“圆柱和圆锥体积、底面积、高之间的关系”来解决问题。从学生平时的练习中经常会发现，学生对解决“等底等高的圆柱和圆锥的体积关系”的相关知识掌握得较好，但是对“底面积相等，体积相等时圆柱和圆锥高的关系”“高相等，体积相等时圆柱和圆锥底面积的关系”则处于一个思维“空白”状态，所以遇到上述习题，常常无从下手。究其原因，这主要是学生的空间观念尤其是直观想象能力的缺失。

为此，笔者对教材资源进行了深度整合，开发了动手“做”数学活动课。旨在为学生提供动手实践的机会，弥补教材中的留白，向学生展示了动手“做”数学活动中蕴含的丰富内涵。

二、探索实践——探寻动手“做”活动的实践路径

学习需要学习思考问题，真正的学习一定是从问题开始的，是从问题以及努力解决问题开始的。“如何做一个和已知圆锥体积相等的圆柱？”便是数学活动的核心问题。真正意义上的“数学活动”是引导学生“做”数学，让学生以有实际意义的工具为中介的“做”来获得知识。通过动手“做”，让学生经历真实的探究过程，促进数学素养的课堂落地。

1.立足认知起点，积累活动经验

活动一：做一个和已知圆锥体积相等的圆柱。

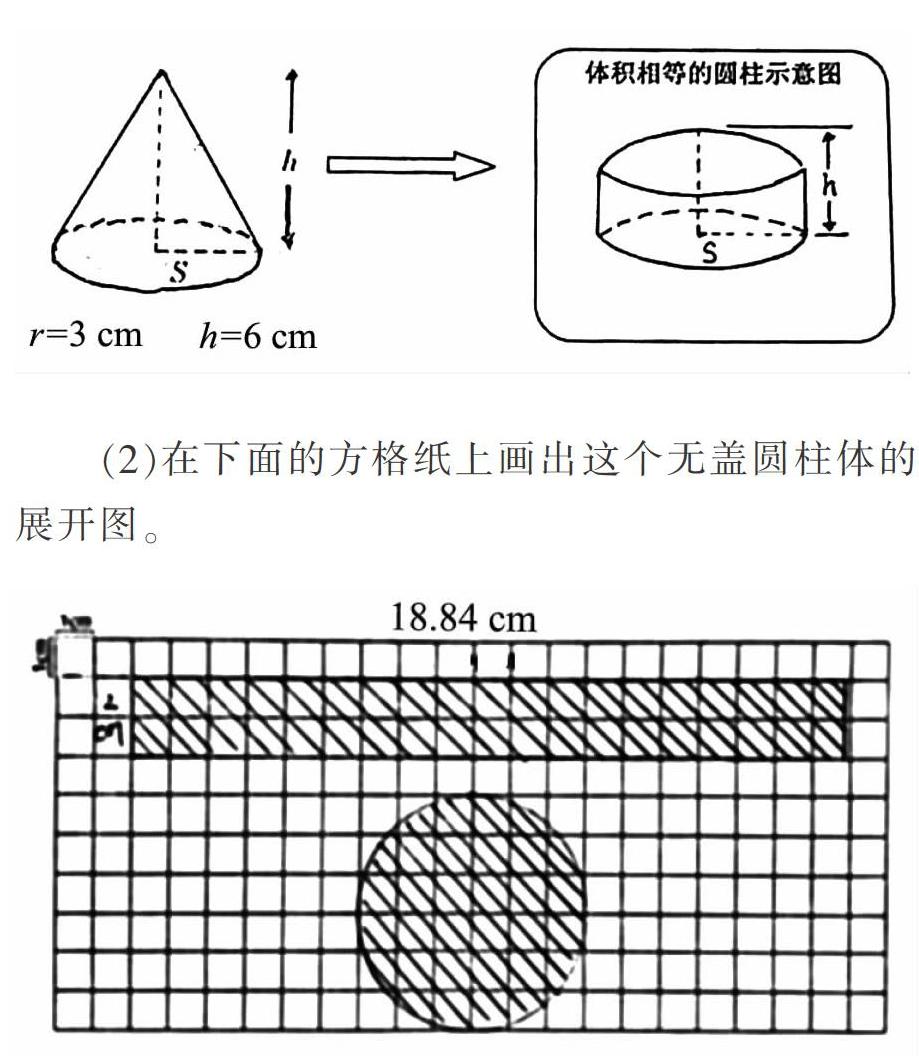
（1）受“圆锥体积是和它等底等高的圆柱体积的”的启发，想象一下：怎样的圆柱和已知圓锥体积相等？试着画出这个圆柱的示意图。

（2）在下面的方格纸上画出这个无盖圆柱体的展开图。

（3）用一张长方形纸，测量出实际所需的数据，动手制作出这个无盖圆柱体纸盒。（侧面可预留粘贴处）

【思考】在学习过程中，学生能做到“做”前有储备，“做”中有思考，“做”后有发现。经历这样的学习过程，不仅能帮助学生获得对数学知识的深入理解，同时也能让他们真切地体会到数学知识形成和发展的内在逻辑。通过之前的圆锥体积研究单，学生对圆锥体积是和它等底等高的圆柱体积的已经有了较深刻的体验。受其启发，学生很容易想到只要画出高度的圆柱，就和已知圆锥体积相等。要完成这个数学活动，还需要掌握相关的操作技能。比如，如何测量圆锥的底面半径和高，如何画圆柱的展开图，如何根据展开图制作圆柱等。学生在画一画、剪一剪、拼一拼的活动中，调动原有的知识储备，积极参与到活动中。学生经历这样的活动过程，才能逐步积累数学活动经验，培养数学思维能力。

2.巧设认知冲突，发展数学思维

活动二：找一找和已知圆锥体积相等的圆柱。

（1）出示1个圆锥和2个自制圆柱纸盒。（如下图所示）

师：根据刚才的学习经验，你能快速找到和这个圆锥体积相等的圆柱吗？

生齐：①号圆柱。

师：当①号圆柱和圆锥具有怎样的关系时，它们的体积才相等呢？

生：圆柱的高是圆锥的，并且底面积相等，它们的体积就相等。

学生上台验证后得出结论：底面积相等，圆柱的高是圆锥的，体积就相等。

师：让我们把目光转向②号圆柱，仔细观察，你有没有什么大胆的想法呢？

生：我觉得也不排除体积相等的可能。

师：那如何才能验证它们的体积是否相等呢？

师：底面积呢？

生：如果圆柱的底面积是圆锥的，体积就相等。

（底面积3倍不能测量验证，只能推理）

师：怎样验证？

生：装沙。

得出结论：高相等，圆锥的底面积是圆柱的3倍（圆柱的底面积是圆锥的）时，体积也相等。

师：看来，要做一个和已知圆锥体积相等的圆柱，有2种方法：一种是确保底面积不变，圆柱的高取圆锥高的;另一种是确保高不变，圆柱的底面积取圆锥底面积的，它们的体积相等。

呈现教材第22页第6题。

……

【思考】吕传汉教授曾就落实数学核心素养提出了“三教”，即教思考、教体验、教表达，并强调“教思考”在发展数学核心素养中的重要地位。当呈现2个圆柱时，学生受思维定式的影响不约而同选择了①号圆柱。此刻，教师适时引导学生观察②号圆柱。启发学生大胆猜想，“②号圆柱会不会和圆锥的体积也相等呢？”“如果相等，它们之间又存在怎样的关系呢？”一石激起千层浪，带着这样的疑问，学生的思维一下子被激活了，进一步探究的欲望逐步深入。学生会通过思维关联，寻找②号圆柱与圆锥的关系，发现高相等，再通过逻辑推理，联想“当高相等时，如果圆柱的底面积是圆锥的，那么它们的体积就相等”。带着这样的猜想开始探究、验证，最终建立了“高相等，圆柱底面积是圆锥的，体积相等”的模型。从而明确：要做一个和已知圆锥体积相等的圆柱，可以有2种方法：一种是底面积不变，圆柱的高是圆锥高的;另一种是高不变，圆柱的底面积是圆锥底面积的，它们的体积相等。教师通过巧妙设置认知冲突，在已有探究经验和成果的基础上搭建思维的台阶，不断激活学生的思维发展空间，从而促进学生更为积极主动地思考。

3.拓宽想象空间，培养创新意识

活动三：想象一个和圆柱体积相等的圆锥。

师：当然，我们也可以做一个和圆柱体积相等的圆锥。同学们，下面让我们一起来做一个活动：看一下你们手里的圆柱学具，把它想象成可以捏的橡皮泥。也可以把你们想象的过程动手画一画。

师：如果要把它捏成一个底面积不变的圆锥形，高会发生怎样的变化？

生：圆锥的高是圆柱的3倍。

师：如果要把它捏成一个高不变的圆锥形，底面积又会发生怎样的变化？

生：圆锥底面积是圆柱的3倍。

根据想象依次呈现如下表：

引导发现：有什么共同的本质特征？（1∶3）

师：真是一个了不起的发现！当“体积、底面积、高”这三者之间有2个等量时，另一个量就是1∶3的关系。

呈现教材第25页第5题。

继续想象：如果圓锥和圆柱的体积比为1∶6，你还能想象出它们之间的关系吗？

呈现教材第23页思考题。

……

【思考】在教学活动中，依据内容特点引导学生积极主动地开展想象，不仅有助于培养学生的空间想象能力，而且能启迪学生的思维和智慧，使学生萌生创新欲望，培养创新意识。

教材第25页第5题，如果以静态的文本方式呈现，学生的错误率通常很高，如果用 “捏橡皮泥”的活动来帮助学生体会“等积变形”的数学思想，学生操作起来也有一定的难度。结合学生刚刚经历的“和圆锥体积相等的圆柱”的活动，引导学生想象：底面不变，高在生长，高不变，底面在扩大……想象是一种脱离了动手操作的更高层次的思维活动，通过想象活动来帮助学生建立“等底等体积”“等高等体积”的模型。这样的想象活动，既有助于发展学生的空间观念，也有助于提升他们的思维品质。通过想象，可以使原本隐蔽的关系明朗化，也可以使原本复杂的关系简单化，从而使静态的文本转化成动态的、丰满的过程。从这个角度来说，想象也是一种十分重要的教学活动策略。

“我听说了，就忘了;我看见了，就领会了;我做过了，就理解了。”这句名言突出了“做”的重要性，深刻地揭示了“探求的意义在于经历”。在课程实施中，作为教师，必须具有整体结构化的课程视野，大胆实践开发课程的意识，这样才能有效引领学生深度建构知识。

上述活动课例的教学，从一个核心问题出发，对问题的加工、拓展，通过三个不同层次的活动，把教材中零散的知识点串成线、织成网，形成了一个系统的知识网络，实现教师与文本、教师与学生、学生与学生的深度互动，为促进“数学核心素养”的落地指明了方向。

【参考文献】

[1]芮金芳.探寻“动手做”数学课程生长的实践路径[J].教学与管理，2016（32）.

[2]朱裕华.深度开发“探索与实践”，发展数学核心素养[J].小学数学教育，2018（24）.

[3]丁元春.在想象中放飞学生的思维[J].小学数学教育，2018（8）.