雷达地物回波建模方法与应用
2020-10-13谢永亮刘尚富
谢永亮 胡 辉 刘尚富
(海军士官学校 安徽蚌埠 233032)
0 引言
实际雷达对地物的显示是一个自然而然的事情,设计人员从来不需要关心地物应该怎样分布、应该怎样显示,一旦雷达设计完成,雷达终端上就会呈现地物回波,这些地物回波可能是孤立的建筑物,也可能是连绵的山脉、广阔的平原,甚至可以是城市、农田等等。可见,地物的显示是一个非常复杂的课题,要模拟出逼真的地物回波,就必须研究地物显示的建模问题,解决好这个问题,是提供逼真的地物回波的必要条件。
当前对地物回波的模拟通常根据雷达的作用距离、分辨力、波瓣和工作频率等参数,结合雷达RCS,对雷达地杂波信号进行数学模型的建立与研究。当前使用的杂波模型主要有三种,第一是杂波幅度和功率谱统计模型;第二是杂波散射单元的机理模型;第三是由试验数据拟合的与频率、仰角、环境参数等参量之间相互作用的关系模型[1]。但这些方法对于将地物转化为雷达显示器上的回波涉及并不多,且研究也未进入深度发展,本文将从入射余角、RCS以及回波的统计特性对地物回波的建模与仿真应用进行研究论证。
1 入射余角对地物回波的影响
地面物体在雷达显示器呈现的回波对雷达操作员来说是干扰杂波,称为地杂波,又可作区域杂波。区域杂波是影响雷达探测的重要因素,尤其是入射余角较低时,这类影响更为明显。其中入射余角、雷达波长、表面粗糙度及其散射特性对雷达杂波散射系数构成的影响最大。从雷达波长来说,雷达波长越长,杂波散射系数σ0越小[2]。入射余角ψg,是波束中心与地平面之间的夹角,如图1所示。

图1 入射余角
σ0与入射余角的关系,一般可划分为:高入射余角区、平坦区和低入射余角区。高入射余角区以相干的镜像反射为主,散射系数随入射余角增大而迅速增大。在平坦区以非相干散射为主,变化趋于缓慢。低入射余角区通常其散射系数随入射余角的增长而飞速增长,又称干涉区[3]。
低入射余角一般指的是从0到临界角附近,比临界角小的表面可看做是光滑的表面;大于临界角的表面可看做粗糙表面[4]。按照瑞利准则,当表面高度起伏的均方根值为hrms,如果满足式(1)时即可将表面认定为平坦表面,即
(1)
如图2所示,当入射波照射到粗糙表面时,由于表面较为粗糙,起伏较大,比起光滑表面的路径而言要长2hrmssinψg,这种路程差可以转换为相位差Δφ,即
(2)
其第一个零点Δφ=π,临界角ψgc可按公式(3)(4)来算出
(3)
或可表示为
(4)

图2 粗糙表面
2 地物回波RCS的计算
地物回波包括从雷达主瓣进入的地杂波以及从雷达副瓣进入的地杂波,所以其雷达反射截面积RCS可表示为σc[5]
σc=σMBc+σSLc
(5)
其中σSLc是旁瓣杂波RCS,σMBc是主瓣杂波RCS,如图3所示。

图3 地物杂波几何示意图
为算出地杂波的RCS,必须先算出主瓣和副瓣对应的RCS。如图4所示,假设目标高度为hr,雷达高度为hr,目标斜距是R,斜距在地平面上的投影由Rg表示,角度θA和θE分别表示方位和垂直维度的3 dB波束宽度,雷达距离分辨率为ΔR,主瓣杂波区的面积由AMBc表示,旁瓣杂波区的面积由ASLc表示。
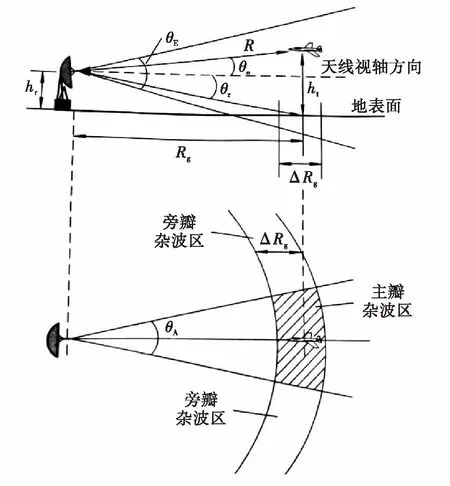
图4 雷达杂波几何图(侧视图和下视图)
由图4可推导出
(6)
(7)
ΔRg=ΔRcosθr
(8)
Rg=Rcosθe
(9)
那么主瓣和旁瓣在杂波区的面积可表示为
AMBc=ΔRgRgθA
(10)
ASLc=ΔRgRgπ
(11)
如果雷达天线的方向图函数为高斯型G(θ)
(12)
那么主瓣杂波和旁瓣杂波的RCS可表示为
σMBc=σ0AMBcG2(θe+θr)
=σ0ΔRgRgθaG2(θe+θr)
(13)
(14)
式(14)中SLrms表示雷达旁瓣电平的均方根值,σ0为地面杂波后向散射系数。
考虑到地球的曲率、传播衰减和大气折射的影响,地物回波的RCS可认为是随距离R变化的函数[6]
(15)
3 地物回波RCS的统计特性
由于地物回波是由数量巨大的随机分布的散射体组成,其相位和幅度均存在随机性,通常用概率密度函数(pdf)来描述此类信号的特性。下面就雷达重点关心的地杂波的统计特性进行研究[7]。
地杂波与天线的照射角密切相关,实际上后向散射系数越大或照射的区域越大,地杂波强度越强。由于地面分布的物体、植被、质地、密度等不一样,会引起地杂波的幅度变化,而这类随机起伏特性在数学上通常采用概率密度函数和功率谱表示[8]。由于地杂波可以看作是数量众多的散射体反射合成的总体效果,因此其统计规律可近似认为是高斯分布[9]
(16)

其幅度模型可用瑞利分布拟合
(17)
(18)
(19)
式中E[·]表示统计平均。
如果在雷达作用范围内,不仅仅存在数量巨大的小散射单元,还有类似角反射器、雷康等强目标时,其统计规律不再符合高斯分布,用莱斯(Rice)分布更能表征其特性
(20)
其中,μ为均值,σ2为方差,I0(·)为第一类零阶贝塞尔函数。
图5就高斯分布、瑞利分布、莱斯分布分别画出了其概率密度函数图。
除此之外地杂波还可以认为是一种随机过程,根据维纳理论,还需要引入其相关特性,通常用功率谱来描述地杂波的相关特性[10]。
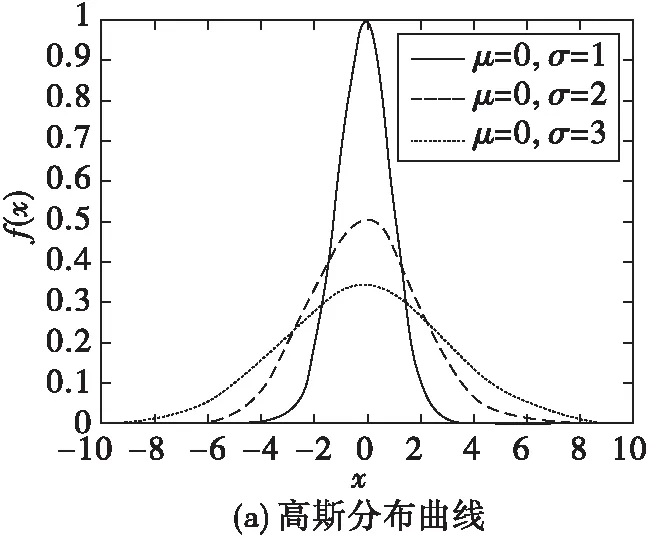

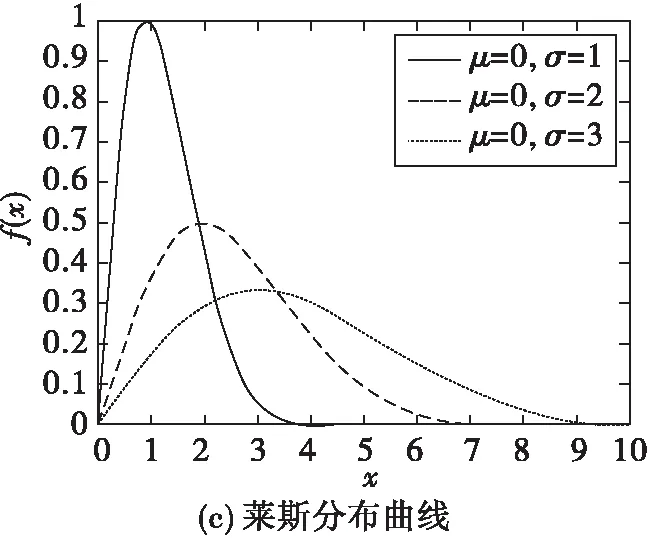
图5 高斯、瑞利和莱斯分布的概率密度函数
一般地,地杂波可以采用高斯谱为
(21)
其中,S0为杂波平均功率,fd为地杂波的中心多普勒频率,σf为地杂波功率谱的标准偏差(谱宽)。
(22)
其中,σν为杂波速度的标准偏差,与地杂波区植被类型和风速有关。
当地杂波中的高频分量比较强时,需要更能拟合高频分量的功率谱函数来表示。通常采用的有全极谱或指数谱。全极谱表达为
(23)
其中,fc称为归一化特征频率,fd为地杂波多普勒频率中心,当n取2是即为柯西谱,当n取3是即为立方谱。
指数谱可表示为
(24)
其中,fd为地杂波的多普勒频率中心,fc称为归一化特征频率。图6分别画出了其对应的功率谱。

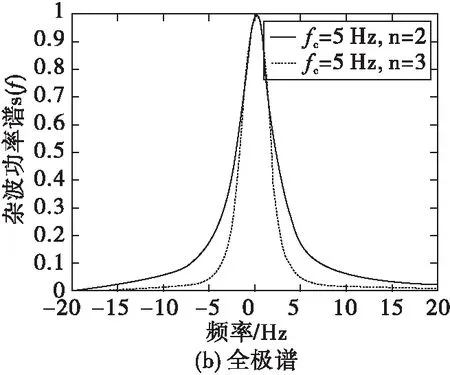

图6 高斯型、全极型和指数型功率谱
4 地物回波模型的仿真应用
模拟地物回波,首先要计算地物的RCS。由式(15)可知,先应计算σc,可采用公式(25)计算[11]
(25)
其中:
σ0—地面杂波后向散射系数;
c—光速;
τ—脉宽(脉压后的宽度);
R—目标斜距;
θ—波瓣宽度,以弧度计算;
φ—入射余角。
假设某雷达τ为2 μs,波瓣宽度θ为2°,设定的地杂波类型为山脉,根据前面的不同入射余角对回波的影响,不同入射余角其对应的后向散射系数σ0见图7所示。
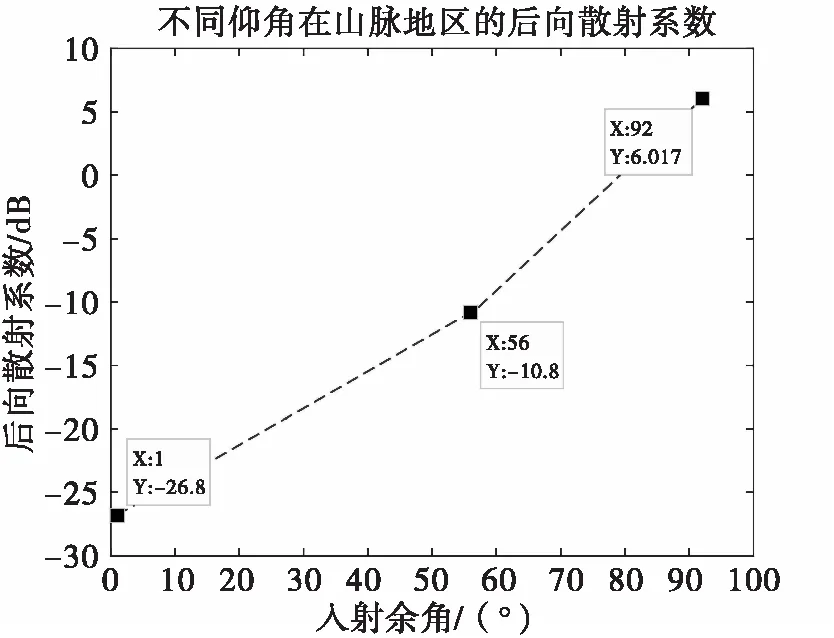
图7 山脉地区不同仰角对应的后向散射系数
入射余角的计算与具体地形相关,对于非山区(城市),地面可以视为平坦地面,地物倾角可以视为0;对于山区,则需要考虑地物的倾角[6]。考虑倾角的情况见图8所示。
图中α为山体倾角,h为山体高度,β为雷达仰角。计算入射余角φ的公式为
(26)
设h为400 m,L为5000 m,则φ是R的变量,其对应关系如图9所示。

图8 地物反射几何模型

图9 入射余角与距离的对应关系
根据以上计算结果,可以由式(15)计算出各杂波位置的等效雷达反射截面积。
计算出地物杂波的等效雷达反射截面积后,就可以开始对地物杂波进行仿真了。首先在地图数据读取地物高程数据,在后台绘制地杂波,通过翻转将绘制的地物杂波图像呈至前台。地杂波的绘制流程如图10所示。
根据扫描线驱动逐个方向进行杂波的计算和绘制,绘制效果如图11所示。从雷达模拟的仿真效果来看,较为逼真地模拟了实际地物的回波,既满足了操作员对雷达环境的直观感受,又满足了杂波中的目标检测操作。

图10 地杂波绘制流程

图11 地物回波在模拟器中的显示效果
5 结束语
在仿真训练与模拟器中,地物回波的模拟是一个重要的环节。本文首先分析了雷达入射余角对地物回波的影响,在此基础上对地物回波建立了相应的数学模型,考虑到地物的起伏性和相关性,加入了地杂波的统计特性,并通过实例仿真模拟了较为逼真的地物回波画面,验证了建模方法的合理性和可操作性。在建模过程中,尚未充分考虑多径效应、天线方向图、脉冲压缩等对地物回波模型的影响,加入这些要素对回波的调制后,模拟效果将与实际回波趋近,这是下一步重点研究的方向。
