基于几何信息辅助的机动目标运动参数快速估计与ISAR成像算法

张 俊 董 锦 宋文青 相 飞 梁晓宇

(西安电子工程研究所 西安 710100)

0 引言

逆合成孔径雷达可以利用固定的雷达天线实现对非合作机动目标的高分辨成像观测，近年来引起了国内外相关领域研究机构的广泛关注[1-4]。

在ISAR成像过程中，如何精确地估计得到目标回波信号的调频率是获得聚焦效果良好的ISAR图像的关键。在这一基础上，一系列距离-瞬时多普勒算法(RID)，诸如相干积累广义立方函数(CIGCPF)算法[5]以及积分广义立方函数(PGCPF)算法[6]等，相继被提出并应用于机动目标ISAR成像方面，并在一定程度上实现了机动目标的高分辨雷达成像观测。但是像CIGCPF等传统的RID算法往往会引入较为明显的传递误差，从而降低目标运动参数估计的精度并导致最终的ISAR图像质量恶化，此外，传统算法往往需要借助搜索的方式来确定运动参数的最佳匹配值，因此会显著增加算法的复杂度，从而不利于算法的工程实现与信号实时处理应用。时频分布函数[7-9]作为参数估计应用中一种广泛应用的有力分析工具，通过对信号按照一定的角度进行旋转变换，能够构筑运动参数与变换角度之间的等价关系，将参数估计问题转化为变换角度估计问题，各项参数之间的估计依赖性被削弱，从而抑制了传递误差对参数估计精度的影响，因此时频分布在对ISAR成像中目标运动参数进行估计时具有得天独厚的优势。但是传统时频分布在估计变换角度时，同样需要利用搜索获取最佳匹配角度，为确保搜索精度，往往需要较小的迭代搜索步长，因此引入的巨大运算量仍然会限制其在工程实现方面的应用。

针对上述问题，本文提出了一种基于分数阶傅里叶变换的机动目标运动参数快速估计与ISAR成像算法。通过分析提取目标调频率与FRFT变换角度之间的几何关系信息，利用其几何信息，快速推导获得FRFT变换角度的估计值，进而利用其与运动参数之间的关系式，计算获得运动参数的估计值，实现最终成像。所提算法在抑制传递误差的同时，能够有效降低算法复杂度，进而实现目标调频率的高效、精确估计。

1 ISAR回波信号模型

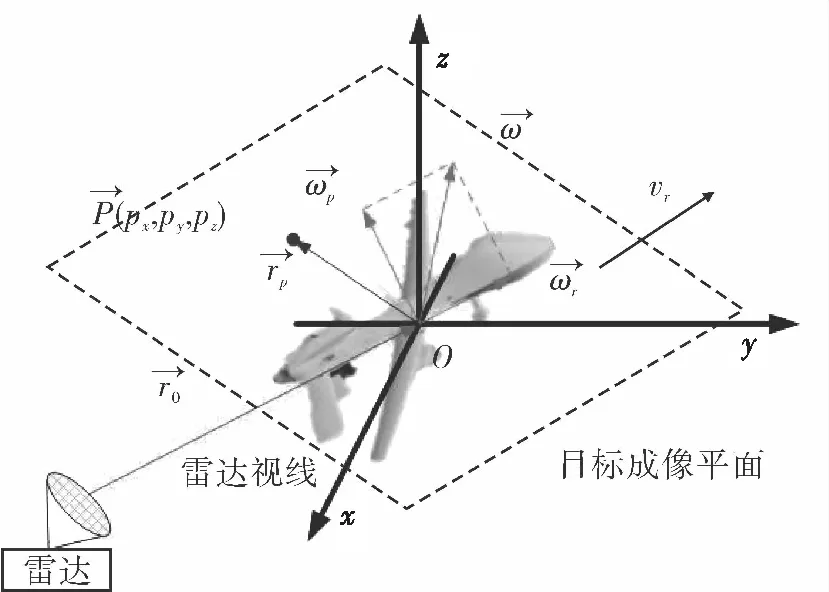
图1 机动目标ISAR成像观测几何模型

(1)

(2)

(3)

(4)

其中，A表示信号幅度项，tr代表距离向快时间，c为光速，Br与Ta分别表示信号带宽与散射点照射积累时间。经过包络对齐与初相校正之后[10-11]，目标上所有的散射点都处于正确的距离单元内，此时第k个距离单元内的第N个散射点关于方位时间的表达式可以改写为

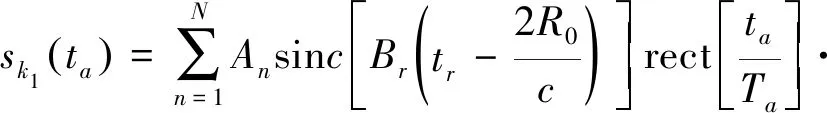
其中

2 基于FRFT的运动参数快速估计与ISAR成像算法

本节在此前引入的机动目标ISAR回波信号模型的基础上开展分析推导，首先将式(5)中的相位项改写为

(6)

对式(6)进行维纳分布(WVD)变换后可得

exp{-j2πfdτ}dτ

=2πδ(2πfd-φ′(ta))

(7)

其中δ(·)，τ与fd分别表示冲激响应函数、时延变量与多普勒频率。将式(7)代入回波信号表达式后，式(5)改写为

(8)

定义机动目标在时频域内的时频变换角度为θ，由式(8)不难看出，经过WVD变换后，线性相位项仅决定WVD投影的位置，其对调频率的估计并没有贡献，因此在接下来的讨论中忽略线性项，主要讨论和分析调频率的估计问题。根据WVD变换的特性，可以建立调频率与变换角度的关系式为

en,2=(λ·PRF)/(4π·Ta·tanθ)

(9)

其中PRF表示系统的脉冲重复频率。由式(9)不难看出，此时目标调频率估计已经被转化为时频变换角度θ的估计问题。传统估计方法此时是通过设定搜索范围与搜索迭代步长，对范围内的所有角度进行搜索以获得变换角度值，这会极大地增加算法的运算复杂度。为降低运算量，在本节中提出了一种FRFT快速估计调频率方法，相应原理与算法步骤将在随后结合图2进行详细的推导说明。

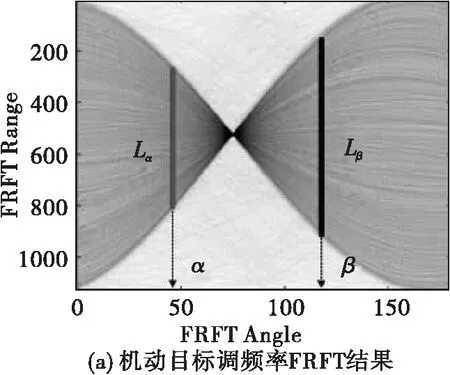
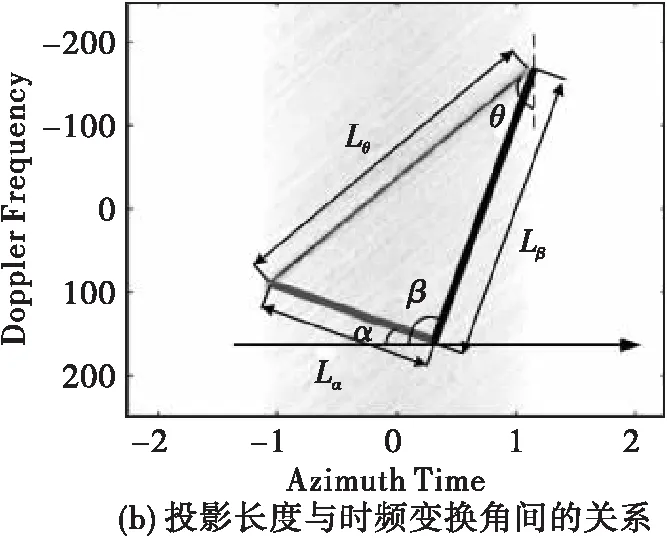
图2 调频率与时频变换间几何关系示意图

图2给出了所提FRFT快速估计算法中所用到的几何信息，相应的仿真系统参数如表2所示。由于FRFT可以看作是目标轨迹沿特定角度转换后的投影，图2(b)中的Lθ代表距离压缩域内的归一化投影长度，由图不难看出，投影长度Lθ与时频变换角θ存在特定几何关系，可以通过测量Lθ长度值推导时频变换角θ，进而估计调频率。但在二维距离压缩域内，归一化投影的长度Lθ往往难以通过测量获得，从而无法通过计算角度θ来实现调频率的估计。因此转换估计思路，通过利用两组FRFT变换角度分别为与的变换结果来消除，进而直接获得时频变换角与两组FRFT变换角的关系式。因此，由图2(b)可以得到

Lθcos(θ-(π/2-α))=Lα

(10)

Lθcos(π-θ-(β-π/2))=Lβ

(11)

其中Lα与Lβ分别表示角度α与角度β时FRFT结果的归一化投影长度。为保证等式(10)与等式(11)能够成立，相关角度需要满足

(12)

式(12)在时频变换角度有限时成立，考虑到ISAR观测机动目标时，其相应的观测角度往往也是一个较小的值，因此式(12)在机动目标ISAR成像中通常成立。将式(10)与式(11)相除并进行改写后，时频角度的正切值可以由式(13)获得

tanθ=-(Lαsinβ+Lβsinα)/(Lαcosβ+Lβcosα)

(13)

因此，利用式(13)估计得到时频转换角度θ后，再结合式(9)，即可快速计算得到调频率的估计值。该算法仅利用两组FRFT变换角度与结果即可快速、准确地实现目标调频率的估计，极大地降低了算法运算复杂度。下面我们通过与其他传统算法的运算复杂度进行比较，验证所提方法在运算量方面的优势。选取典型的CIGCP、PGCPF与传统二维搜索FRFT算法与所提算法进行对比。假设M表示变换角度个数，N表示方位维采样点数，具体的算法复杂度在表1中给出。

表1 各算法运算复杂度对比

由表1可以看出，所提算法由于避免了搜索处理，因此算法复杂度相比于其他算法显著降低。此外，在实际处理过程中，经过平动补偿后的回波信号往往会存在一定的剩余相位项(如线性相位项与高阶相位项等)，这些剩余相位所引起的传递误差在传统算法的估计过程中，会对调频率的估计精度产生影响。但是所提算法仅受信号的多普勒调频率影响，即仅依赖于图2(b)中，目标时频变换投影轨迹的斜率，所提算法的这一特性能够有效避免传递误差的影响，进而保证最终参数估计的精度。

3 仿真实验与实测数据处理结果

在本节中，首先利用仿真数据对所提算法进行验证。表2给出了仿真实验系统参数设置，仿真采用的机动目标模型为飞机模型，共计由39个散射点组成，具体形状如图3所示。

表2 仿真实验系统参数

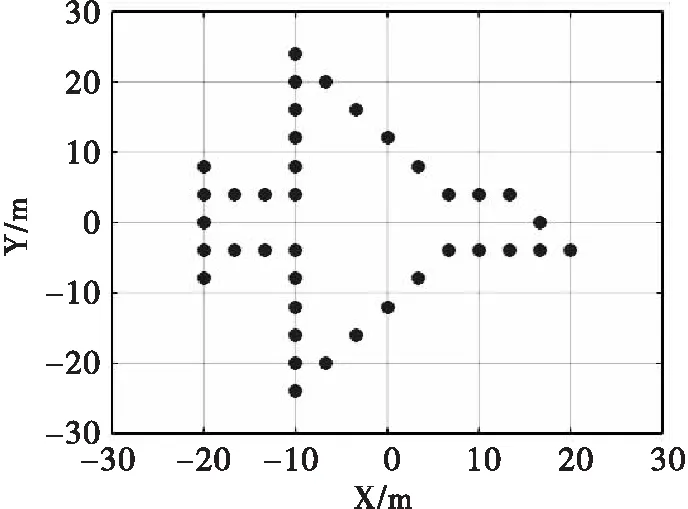
图3 仿真机动目标几何结构模型

在对仿真回波信号进行距离压缩与运动补偿后，消除了距离徙动，并使得所有散射点均处于正确的距离单元内，便可以进行后续运动参数估计。图4给出了场景信噪比为SNR=8 dB时，利用不同算法得到的仿真目标ISAR成像结果。

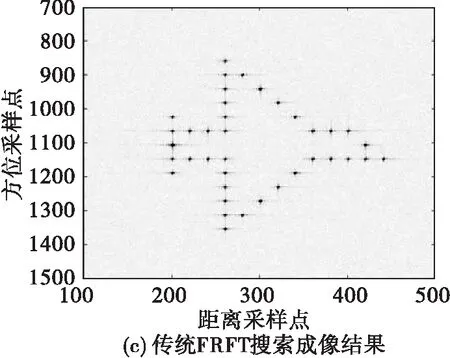
图4 SNR=8 dB时各算法仿真目标成像结果

由图4不难看出所提方法与传统算法对仿真目标进行处理成像时，均能获得较好的成像结果，但相较于传统算法，所提方法获取图像时间明显缩短，这里引入图像熵值[12]对成像结果进行评估，在表3中给出了图像的熵值与相应获取时间，由表中数值不难看出，所提算法得到的图像熵值与传统搜索算法获得的图像熵值十分接近，但其所需的成像时间却远小于传统算法，这一点也再次验证了所提算法在算法运算量方面的优势。

表3 仿真实验成像性能参数指标

下面我们利用实测数据再次对所提算法进行验证，外场实验的背景噪声水平约为-4 dB，观测目标为一非合作机动飞机，雷达系统参数如表4所示，目标运动参数未知。

表4 实测数据系统参数

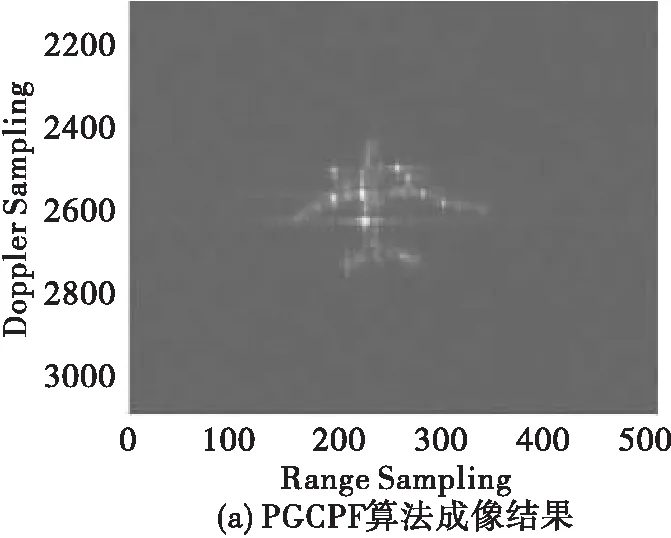
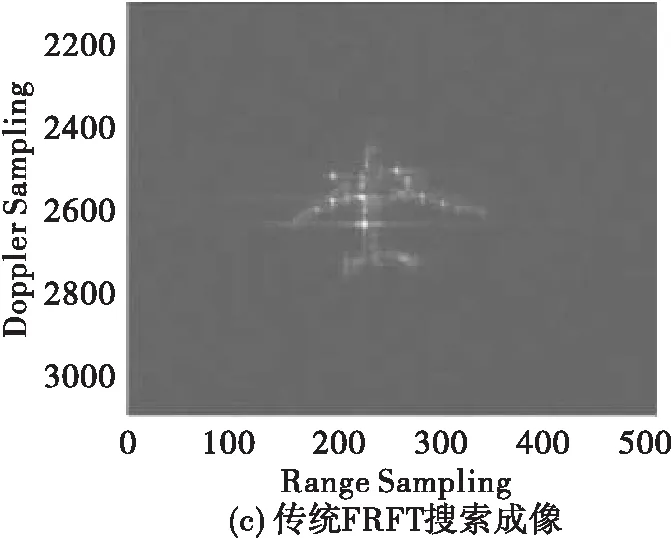
图5 各算法实测数据处理成像结果

图5给出了各算法处理实测数据后获得的成像结果，可以看出，由于存在传递误差的影响，PGCPF与CIGCPF算法处理获得的图像质量会出现下降。同样利用熵值对各幅图像的成像质量进行对比评估，具体的图像熵值、调频率估计值与处理所需时间均在表5中给出。可以看出所提算法获得的ISAR图像熵值低于PGCPF与CIGCPF，但要比传统FRFT搜索算法(搜索次数1000)略高，但所需时间远小于搜索算法。所提算法实现了图像精度与处理时间两者之间的折中，这也验证了所提算法在实际工程应用中的优势。

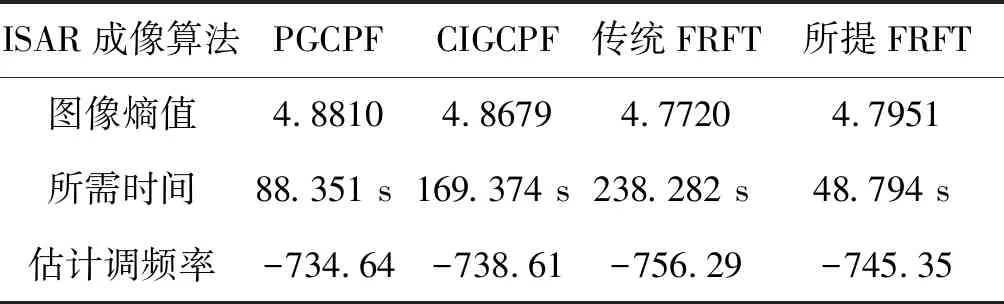
表5 实测数据成像性能参数指标

4 结束语

本文提出了一种基于FRFT的机动目标运动参数估计方法来实现多普勒调频率的快速估计与目标的高分辨成像。所提方法通过几何信息辅助的手段，在显著降低算法运算复杂度的同时，有效避免了传递误差的影响，实现了图像精度与运算量二者之间的折中，保证了最终参数估计的精度与所获得ISAR图像的分辨率。最后通过仿真实验与实测数据验证了所提算法的有效性与正确性。