基于零点插入法的带通FSS矩形系数改进
2020-10-13穆依飞李存龙
穆依飞 李存龙
(西安电子工程研究所 西安 710100)
0 引言
频率选择表面是由周期排列金属贴片或者孔径单元组成的二维结构,对电磁波的频率具有选择特性,但本身并不吸收能量,本质就是一种空间滤波器[1]。其在隐身雷达罩、吸波材料和反射面天线中有着广泛的应用[2-3]。带通FSS作为隐身雷达罩时,其主要原理是保证己方雷达频段的电波自由传播,而反射敌方雷达频段的电波,通过雷达罩的低RCS外形将敌方电磁波反射到四周空间,从而提高飞行器的隐身性能。所以设计具有良好滤波矩形系数的带通FSS具有重要的意义。
国内外关于带通FSS的滤波矩形系数的提升也有不少研究,大多数研究者的方法是多层孔径FSS的级联,但其并不能大幅提升带外性能,而且在一定程度上会影响通带性能[4-5]。部分学者也尝试通过复杂FSS单元来提升这一性能,但是也存在影响通带性能的弊端[6]。
本文旨在利用零点插入法设计一种具有良好滤波矩形系数的带通FSS。首先基于等效电路法验证了级联带阻FSS的零点插入法提升带通FSS滤波矩形系数的可行性。然后设计了以方环为基本单元构成的贴片-孔径-孔径-贴片四层FSS级联结构,并通过等效电路法建立其等效电路模型,与仿真结果作对比,分析其滤波机理,最后通过与双层孔径FSS的对比,验证了该设计方法的有效性。
1 ECM分析
在分析FSS的众多方法中,等效电路法是一种简单并且有效的方法。其基本原理是将FSS单元中的缝隙等效为电容,将窄带金属条等效为电感,从而将贴片型FSS等效为LC串联结构,将孔径型FSS结构等效为LC并联结构[7-8]。介质层的等效模型为传输线。
1.1 零点插入法的可行性验证
零点插入法是指通过一定的设计方法在FSS的传输曲线上引入传输零点,而达到特定的效果[9]。本节将这种思路运用到提升FSS滤波矩形系数的设计之中。尝试在通带的低频端和高频端分别引入传输零点,从而使得带通FSS具有更好的滤波特性。以下是对这一思想可行性的验证。
验证思路如图1所示,通过在带通FSS的一侧级联一阶带阻FSS。
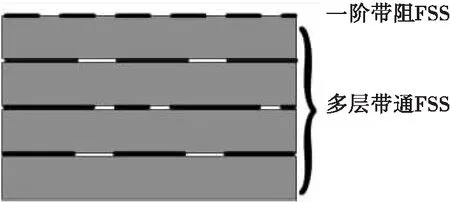
图1 带通FSS级联一阶带阻FSS
若在低频端引入零点,则对于多层带通FSS(包含介质层),其在低频端呈现出感抗特性。所以其在低频端的等效电路模型可以简化为图2。

图2 等效电路模型
其中L1C1串联电路为一阶带阻FSS等效电路模型;L为带通FSS在高频端的等效电路模型;Z0为自由空间阻抗。
图2所示电路网络为纯导纳型网络,其传输系数为
(1)
其中,
(2)
(3)
当|Y|=0时为传输极点,而当|Y|=时为传输零点。

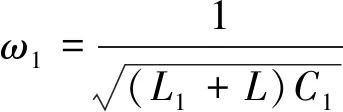
显然ω1<ω0。所以在传输零点ω0的低频端会存在一个传输极点ω1。
同理若尝试在高频端引入零点,则带通FSS呈现出容抗特性,经过类似推理,发现其也会在插入零点位置的高端产生一个传输极点。
在带通FSS设计中,低频端出现极点是不允许的,而高频端出现极点可通过控制极点的位置,让极点处于考察频段之外,也可以通过多个零点的引入来抑制这一极点在考察频段出现。
综上所述,Teach-Back 健康教育模式适合手足口病患儿家属,能有效提高其对疾病的认识和促进其采取健康行为。在临床护理工作中,应加强对护理人员的培训,增加其对Teach-Back健康教育方法的运用,提高健康教育效果。
综上所述,通过给带通FSS级联带阻型FSS在低频端插入零点的方法是不行的,而在高频端插入零点的方法是可行的。
1.2 PAAP结构ECM分析
本节设计了一种具有良好边缘陡降性的带通FSS,基本结构为以方环为基本单元构成的贴片-孔径-孔径-贴片(patch-aperture-aperture-patch,PAAP)四层FSS级联结构。设计思想是使用两层孔径级联可以在一定程度提升低频端滤波矩形系数,使用两层贴片结构可以在高频端插入两个不同的零点,形成宽阻带,从而提高高频端滤波矩形系数。
该结构侧视图如图3所示。FSS1与FSS4分别为贴片型,FSS2与FSS3分别为孔径层。各层FSS的单元示意图如图4所示。
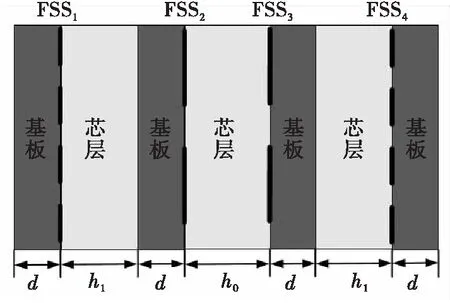
图3 PAAP模型结构图
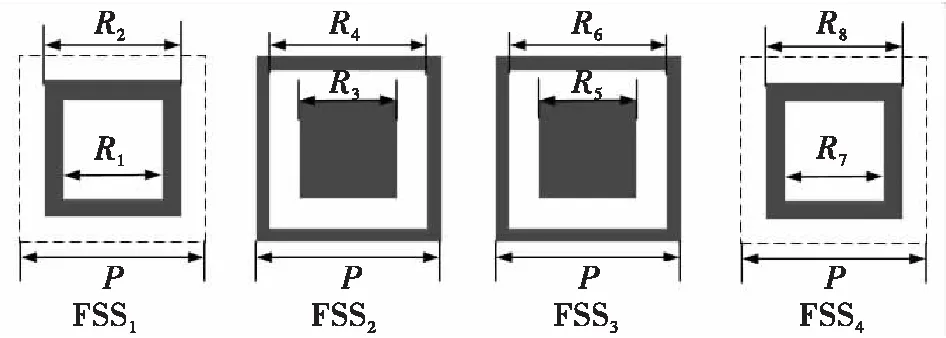
图4 各层FSS单元示意图

图5 PAAP等效电路图
其等效电路模型如图5所示,FSS2和FSS3构成等效电路中的LC并联电路,与其中间的传输线构成二阶带通滤波器,而FSS1和FSS4构成等效电路中的LC串联电路,将在高频端提供两个不同的传输零点f01与f02。
其中,
(4)
(5)
图5中Z0=377Ω,为自由空间的特性阻抗。Z1与Z2分别为芯层和基板等效为传输线后的特性阻抗。所以有
(6)
(7)
所以对于第一层与第四层贴片型FSS的归一化容抗和感抗分别为[10]
(8)
(9)
(10)
(11)
(12)
同理可推导出第二层与第三层孔径型FSS的归一化容抗和感抗分别为
(13)
(14)
(15)
(16)
其中
(17)

(18)
(19)
(20)
根据传输线理论,可计算出图5中所示的等效电路网络左端口的输入阻抗ZL。由反射系数公式可计算出该网络的反射系数为
(21)
由于所设计的结构使用的基板和芯层都是低损耗材料,可忽略。所以根据传输系数与反射系数的关系为
(22)
可以计算出其传输系数τ的模值。
2 算例验证与分析
设置图3中芯层的相对介电常数为εr1=1.1,损耗正切为tanδ1=0.001,基板的相对介电常数为εr2=2.65,损耗正切为tanδ2=0.001。通过调节图4中的各参数可控制通带位置与零点分布,各参数最终的优化取值如表1所示。

表1 各参数取值(单位:mm)
图6为PAAP结构在电磁波垂直入射下时的ECM结果与CST仿真结果对比图。发现ECM计算的结果与CST仿真结果在1~13 GHz具有很好的吻合性,而在在高频端,零点位置具有一定差异。原因在于不同层FSS之间存在耦合,尤其存在耦合电感,使得实际电感值大于等效电路中的电感值,所以导致实际FSS中插入的零点位置要低于等效电路模型中插入的零点位置。
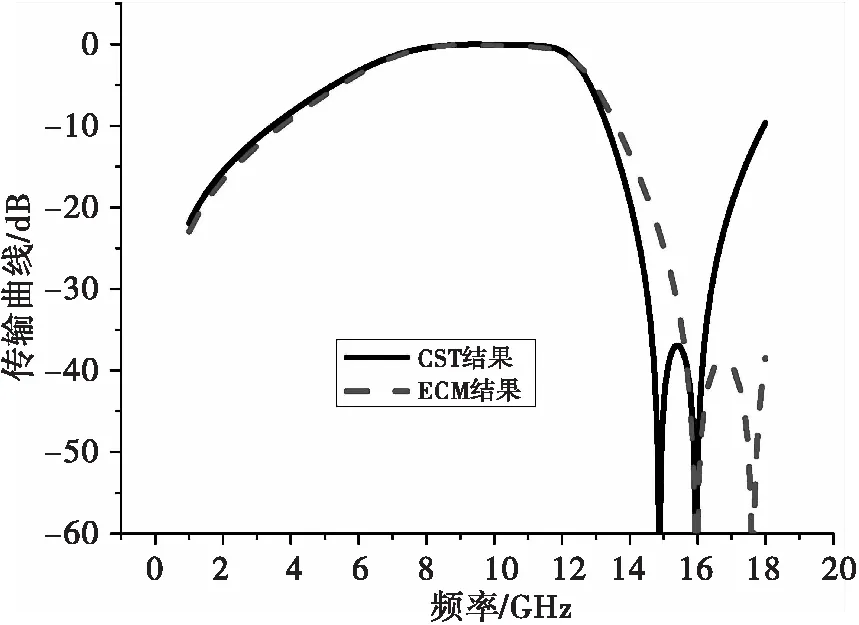
图6 CST仿真结果与ECM结果对比

图7 双层孔径结构侧视图与单元示意图

表2 各参数取值(单位:mm)
为了显现PAAP结构的良好滤波性能,同样设计了具有同样带宽(8~12 GHz)的以方环为基本单元的双层孔径FSS。双层孔径的模型如图7所示,结构参数如表2所示。图8、图9、图10分别为双层孔径与PAAP在0°、30°、60°电磁波入射角下的传输系数对比图。从图中可以发现,不管在多少入射角下,PAAP结构具有更加良好的滤波矩形系数,从而验证了这一设计思想的可行性和有效性。

图8 双层孔径与PAAP传输系数对比图(0°角入射)
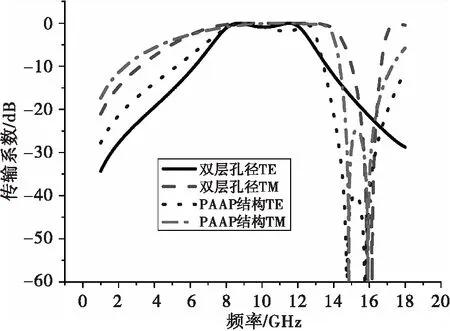
图10 双层孔径与PAAP传输系数对比图(60°角入射)
3 结束语
本文基于插入零点的思想,首先证明了通过给带通FSS级联带阻FSS的方式来提高其滤波矩形系数,在低频端是不可行的,因为其总会产生一个比零点位置更低的极点,而在高频端是可行的。继而设计了一种以方环为基本单元的贴片-孔径-孔径-贴片四层FSS级联的结构,并且通过等效电路法对这一结构进行了分析,从电路角度解释了这一设计思路的可行性。最后通过具体的算例,并与具有相同带宽的双层孔径FSS作对比,验证了这一设计方法的有效性。
