航天项目计划缓冲区尺寸确定方法研究
2020-10-13张沁生赵长见程永欣
张沁生,赵长见,赵 蕊,李 璞,程永欣
(中国运载火箭技术研究院,北京,100076)
0 引 言
新一代智能技术与航天技术的深度融合正在成为中国由航天大国走向航天强国的重要驱动,新一代项目管理智能信息化系统的发展也同步成为航天项目管理的热点问题。
关键链法提供了一种新的项目管理方法,相对传统关键路径法(Critical Path Method,CPM)或计划评审技术(Project Evaluation and Review Technique,PERT)的改进点在于在约束理论基础上实现了计划与资源的紧密结合。历经20 余年的发展,其理论逐渐被引入实际应用,但其先进性仍主要体现在管理思想方面,许多重要理论方法在实际应用中仍存在普适性不足的问题。
将关键链法应用于新一代航天项目管理信息化系统中需要解决多方面的问题,包括航天多级计划中哪几级应用关键链法、长周期型号项目缓冲区(项目缓冲、汇入缓冲、资源缓冲)设置问题、多项目计划的智能优化、多项目计划智能再调度以及多项目计划的鲁棒性等一系列问题。所有问题的最基本元素是活动的工期估计和各类缓冲区确定。
1 问题分析
1.1 航天项目科研生产活动分类及特点
依据“研制程序”等行业规范,项目科研生产直接相关活动主要分为:设计类(含技术创新与工艺创新)、产品生产类、试验类和验收评审类。通过分析历年来部分型号项目的各类活动完成工期,并与部分项目管理人员研究,总结了上述4 类活动工期特点:
a)设计类:工作分解结构中各活动由设计人员单独或与其他设计人员协调完成。其不确定性较大,主要取决于技术难度、人员的水平、态度及人员间的相互配合程度。多型号的此类活动实作工期数据统计分析显示,完工工期基本呈正态分布或略左倾的正态分布。“帕金森法则”、“学生综合症”等确实在一定程度上影响着工作的完成。
b)生产类:各类活动主要指各种产品或试验件的生产,其活动内容及时间由生产工艺进行规范,该类活动的完工工期有一定的刚性。不确定性主要来源于生产准备时间、人员操作熟练程度等。该类活动的完工工期统计数据呈右倾较多的正态分布,或以对数正态分布拟合更为恰当。
c)试验类:指利用试验设备、设施,按试验大纲规定完成试验,取得各类试验参数,供设计人员确定和调整设计状态。其不确定性主要来源于操作人员、试验进程是否符合预期等。不确定性介于设计类和生产类之间,完工工期统计数据呈现略右倾的正态分布。
d)验收评审类:经对统计数据分析,该类活动工期通常较短,确定性较高,可以将估计工期直接设置为计划的执行时间,不设置缓冲区。
主要类型活动的完工工期概率密度如图1所示(不包括评审验收类)。
1.2 缓冲区大小确定常用方法
关键链法缓冲区大小的确定通常采用“剪切-粘贴法”或“根方差法”。
“剪切-粘贴法”[1]由关键链法创始人Goldratt 提出,将活动执行时间设定为估计工期值的50%,将关键链或非关键链的各活动工期剪去部分的1/2 作为安全时间,求和后直接放置在关键链尾或非关键链尾,作为项目缓冲(Project Buffer,PB)或汇入缓冲(Feeding Buffer,FB)。此方法自提出之日起就颇具争议,文献[2]~[6]从不同侧面做了论述,项目缓冲、汇入缓冲都随着计划网络复杂度增加和活动数量增多而呈线性增长,与项目实际严重脱节。
根方差法[2]由Newbold 提出,主要目的是解决“剪切-粘贴法”缓冲区随链上活动线性增长问题。具体方法是以估计工期的50%作为执行时间,将核减的时间作为安全时间σi,对关键链或非关键链上各活动安全时间的平方和开平方,放置链尾形成项目缓冲PB 或汇入缓冲FB。其计算式为
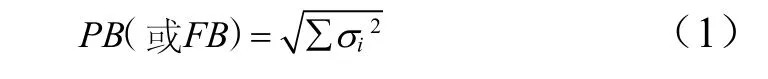
林晶晶[3]认为:根方差法提出的各活动相对独立的基本假设并不符合实际;张文静等[4]认为“根方差法”与“剪切粘贴法”一样,都未考虑资源约束的松紧度。
1.3 航天项目缓冲区确定需解决的首要问题
a)执行时间应符合航天项目各类活动工期分布
王雪青等[5]提出不应简单地将安全时间设定为估计工期的50%,缓冲区大小确定应考虑人员、设备、技术、风险等因素的影响。蔡晨等[6]在三点估值法基础上,设置弹性系数KB,通过KB计算安全时间。
航天项目3 类主要活动呈现出不同的工期分布特征,统一以估计工期的50%划分为执行时间和安全时间不符合航天项目实际。上级计划按此考核下级执行单位,对生产类、试验类工作则过于严苛、失实,不仅于任务完成无益,而且可能造成管理混乱。
b)多项目计划的鲁棒性问题
航天项目管理信息化系统,安排着众多的型号科研生产任务,各型号、各项目的众多活动存在对同一资源的争夺。为平衡竞争,在计划制定之初就依据设定的各活动工期进行了多项目计划的优化与反复协调。在执行过程中,如果由于活动工期严重失准,导致前项计划未按期完成,必然造成后续计划节点的批量调整。如果此现象在众多型号中普遍存在,必然造成多型号、多项目普遍进行计划的再调度和再优化。计划的大面积、频繁变更不仅造成计算资源大幅浪费,也将导致系统失败和项目管理失控。
面对上述问题,基于中心极限定理,忽略各活动工期分布特征,将缓冲区大小建立在统一的正态分布基础上,简单地将各活动估计工期的50%设定为安全时间显然是不可行的。
为解决这一问题,需要寻找更为灵活、符合航天项目各类活动实际完工工期分布特点的执行工期、安全时间及缓冲区大小的确定方法。综上,航天项目计划缓冲区确定方法应满足下述基本条件:
a)活动工期估计、执行时间确定、缓冲区大小计算方法应能够利用活动完工工期统计数据和经验,符合航天项目不同类型活动的完工概率密度分布特征;
b)以新方法编制的关键链法计划,不必追求项目纸面计划的尽可能短,而应为实际执行计划和多项目执行计划具有高鲁棒性提供必要的基础;同时,新方法计划也应体现关键链法的先进思想。
2 缓冲区大小确定
2.1 基于模糊理论的执行时间确定
项目工作分解结构中任意一项活动的执行时间及安全时间都源于对该活动的工期估计。活动的工期估计一般由经验丰富的项目管理人员依据经验主观估计,不可避免地具有模糊性。将模糊数学引入活动工期估计,能较贴切地描述和处理这种模糊性。
2.1.1 模糊数简介
模糊数学基本理论将模糊数定义为一个连续的模糊集合[7,8]。描述活动工期通常采用梯形模糊数和三角形模糊数,梯形模糊数形式如图2 所示。
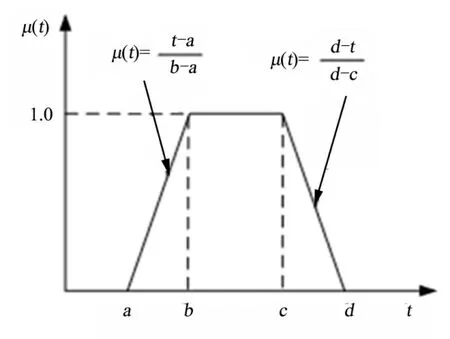
图2 梯形模糊数Fig.2 Trapezoidal Fuzzy Number
梯形模糊数(a,b,c,d)的隶属函数表达式为

式中 μ(t) 为隶属函数;t 为活动执时间。
2.1.2 一致指数
一致指数最早由Gupta 和Kaufmand[9]提出,被用来评价两个模糊事件的一致程度。其实际含义为描述模糊事件A 有多大比例分布在事件B 的区间中。两个事件A、B 的一致指数AI(A,B)面积表达式为

式中 μ(A∩B)为模糊数A 与模糊数B 交集的隶属函数;μ(A)为模糊数A 的隶属函数。
一致指数AI(A,B)指标的面积表示如图3 所示。设定项目工作分解结构中某一活动A(事件A)的工期估计为梯形模糊数(a,b,c,d);同时假定事件B 的模糊数为(0,0, th, th),则Area(A ∩ B)为图中阴影部分的面积,一致指数AI(A,B)为阴影部分面积除以梯形(a,b,c,d)的面积。
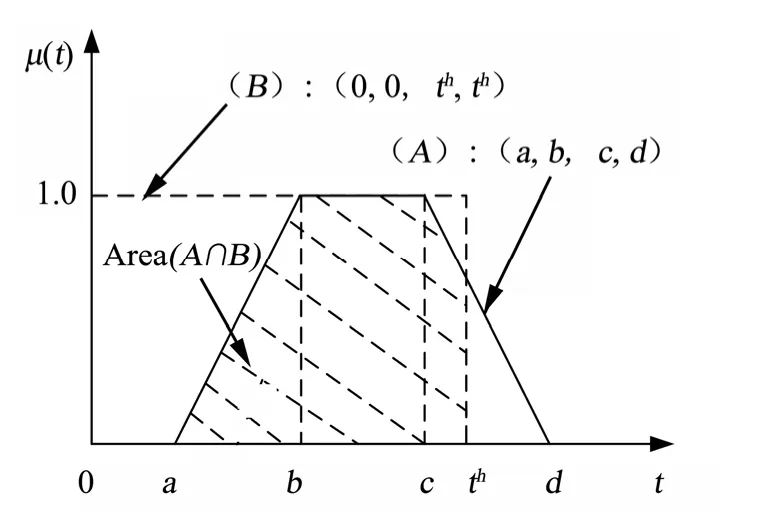
图3 一致指数的含义Fig.3 The Meaning of the High Agreement Index
性质1:0≤AI(A,B)≤1
性质2:AI(A,B)= f ( th)
2.1.3 执行工期确定
将梯形模糊数引入项目活动工期估计,梯形模糊数(a,b,c,d)对应的完工可能性如表1 所示。

表1 梯形模糊数表示的完工可能性Tab.1 Probability of Task Completion Indicated by Trapezoidal Fuzzy Number
梯形模糊数b,c 取值相等时,就转化为三角形模糊数,因此“三点法”可以看作“梯形模糊数法”的一个特例。
工期估计的四点分布需结合历史经验、活动类型、技术成熟度、活动不确定性等因素,应体现被评估活动完工概率密度的基本特征。
在文献[9]~[10]的基础上得出以下定义:
一致指数AI(A,B)反映的是:在 th时刻活动A的完工概率。若令h=AI(A,B),此时 th为完工概率为h 时活动A 的执行时间,称h 为活动A 的真度值。
由表1 可知,活动的执行时间th取值范围仅应在(b,c)或(c,d)区间内。
由假设条件及式(3),可推导出:
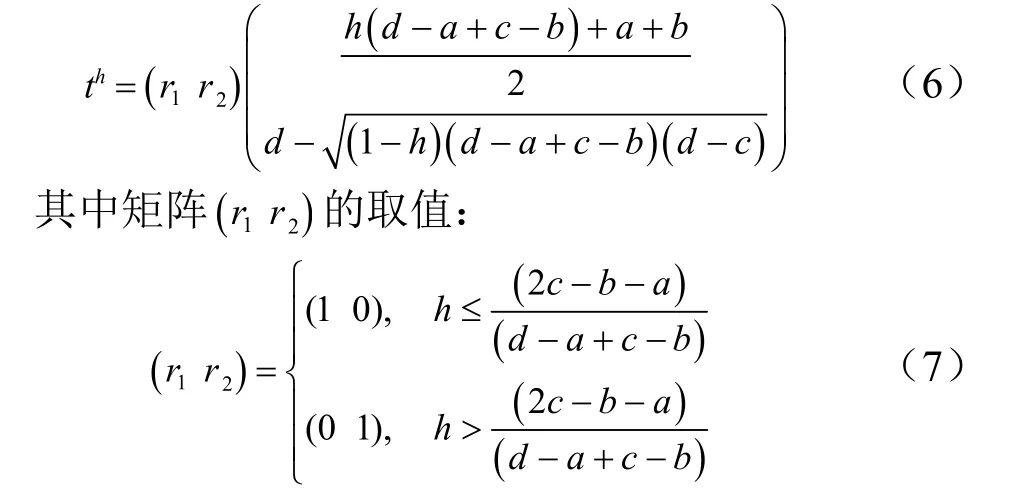
活动执行工期的分类计算:
a)新技术(新工艺)开发或应用等类型活动:主要归类为设计类活动,真度值h 取50%,活动执行时间可取t50%;
b)试验等类活动:真度值h 取55%,活动执行时间取t55%;
c)生产等类活动:真度值h 取60%,活动执行时间取t60%。
验收评审类工作与其它类型活动相比,通常时间较短,可以将估计工期作为执行时间,不设定安全时间裕量,不计入缓冲区。
本文仅基于部分统计数据和经验总结,对有关类型活动真度值h 选取给出概略性建议。更合理、准确的选取值有待大量各类活动实际执行时间的积累和分析。项目管理人员可依据经验、历史数据积累以及具体活动的不同特点等选取具体活动的真度值h。
通过真度值h 的调整,项目管理人员能灵活地应用活动的完工概率积累数据,确定活动的执行时间th,从而使计划更符合实际,有利于提高实际执行计划的鲁棒性。
2.2 缓冲区大小计算
2.2.1 安全时间裕量与风险因素
活动的安全时间裕量:

式中si为活动i 的安全时间裕量; di为活动i 估计工期的最大值; thi为活动i 的执行时间。
决定缓冲区大小的因素除安全时间裕量外,还有影响各活动执行的风险因素,主要有资源不确定性(αi)、网络活动复杂度(βi)、技术不确定性(δi)及环境不确定性等。
资源不确定性是指被评估活动所需资源(人力、设备及设施等可更新资源)的保障程度,其评价指标多以资源紧张度(αi)表示[3]。
网络活动复杂度是指:距离项目开始时间越远的活动,其工期估计的不确定性越大。其评价指标以网络活动复杂度(βi)表示[3]。
技术不确定性:活动包含新技术开发或应用,理论的成熟性、新技术的实现途径、作用机理、对环境的适应性以及应用结果等都会对活动完成时间造成较大的影响。为定量化表示技术不确定性,部分研究采用了层次分析法。该方法的评价指标打分、权重的确定是主观的,计算过程也相对较多。本文采用经验设定,即参照其他项目历史数据,对特定的活动可设定技术不确定性系数(δi)为0.2~0.5 的一个经验系数。
环境的不确定性,是指用户要求、项目实施环境变化等对活动的影响,具有不可预测性,一般采用临时应对措施,不在缓冲区计算中考虑。
2.2.2 缓冲区大小计算
确定缓冲区大小的步骤是:a)计算各活动执行时间;b)依据紧前、紧后关系,结合资源约束绘制网络图,确定关键链、非关键链;c)确定插入汇入缓冲及项目缓冲的位置;d)计算项目缓冲PB 及汇入缓冲FB。
综合各风险因素影响,项目缓冲与汇入缓冲大小的计算公式为
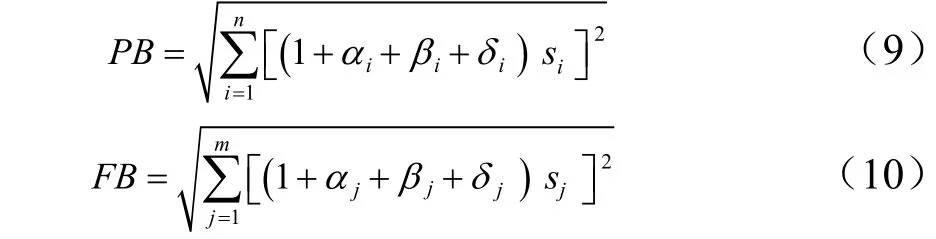
式中 PB 为项目缓冲;i 为关键链上所有活动(1,2,3…,i,…,n-1,n)的第i 项;n 为关键链上所有活动的最后一项;αi,βi,δi和si分别为关键链上第i 项活动的资源紧张度、网络活动复杂度、技术不确定性系数和安全时间裕量;FB 为汇入缓冲;j 为某一非关键链上所有活动(1,2,3…,j,…,m-1,m)的第j 项;m 为某一非关键链上所有活动的最后一项;αj,βj,δj和sj分别表示此非关键链上第j 项活动的资源紧张度、网络活动复杂度、技术不确定性系数和安全时间裕量。
2.3 缓冲的检验与调整
非关键链汇入关键链如图4 所示。
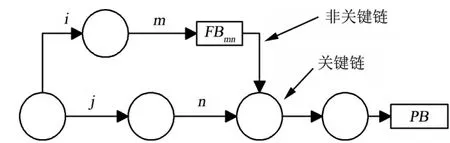
图4 非关键链汇入关键链示意Fig.4 Schematic Diagram of Non Critical Chain and Critical Chain
将关键链各项活动及项目缓冲向右靠齐,非关键链各项活动向左靠齐;汇入缓冲的大小须满足:
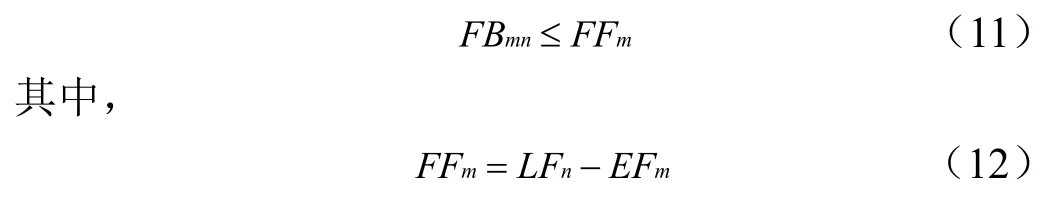
式中 FBmn为非关键链活动(i~m)的汇入缓冲;FFm为非关键链上最后一个活动m 的自由时差;LFn为关键链上活动n 的最晚结束时间;EFm为非关键链上活动m的最早结束时间。
若不满足式(11)要求,则令 FBmn=FFm;否则此汇入缓冲将导致关键变更和项目完工时间推迟。
3 算例
3.1 项目基本信息
算例网络图如图5 所示。
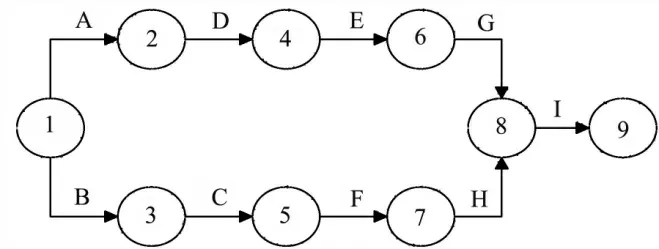
图5 算例网络Fig.5 Network Graph of the Example
算例的工作内容、资源、工期估计如表2 所示。
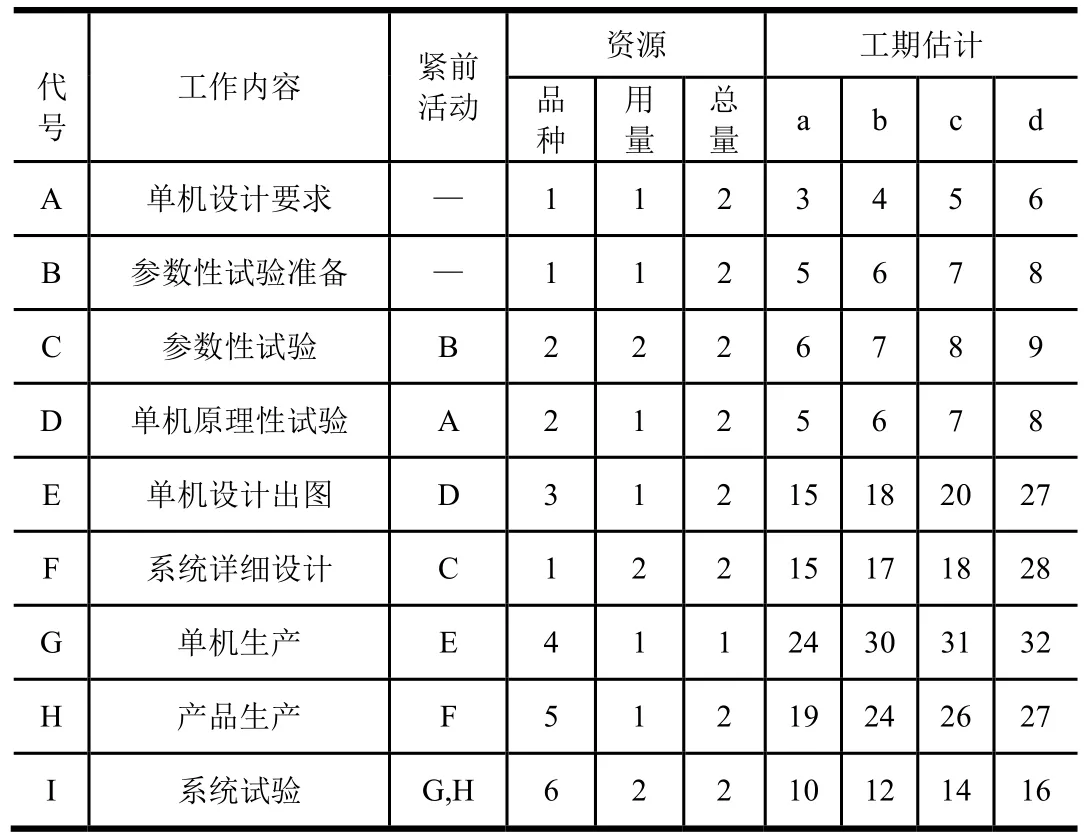
表2 算例基本信息Tab.2 Basic Information of the Example
其关键路径为B-C-F-H-I,以活动估计工期的期望值为执行工期,关键路径法求得的算例项目总工期为70.17 个时间单位。此关键路径未考虑活动C 与活动D的资源冲突,实际此关键路径不可执行。
3.2 缓冲区尺寸计算
不同方法计算所得各活动执行时间、安全时间裕量具体数值如表3 所示。
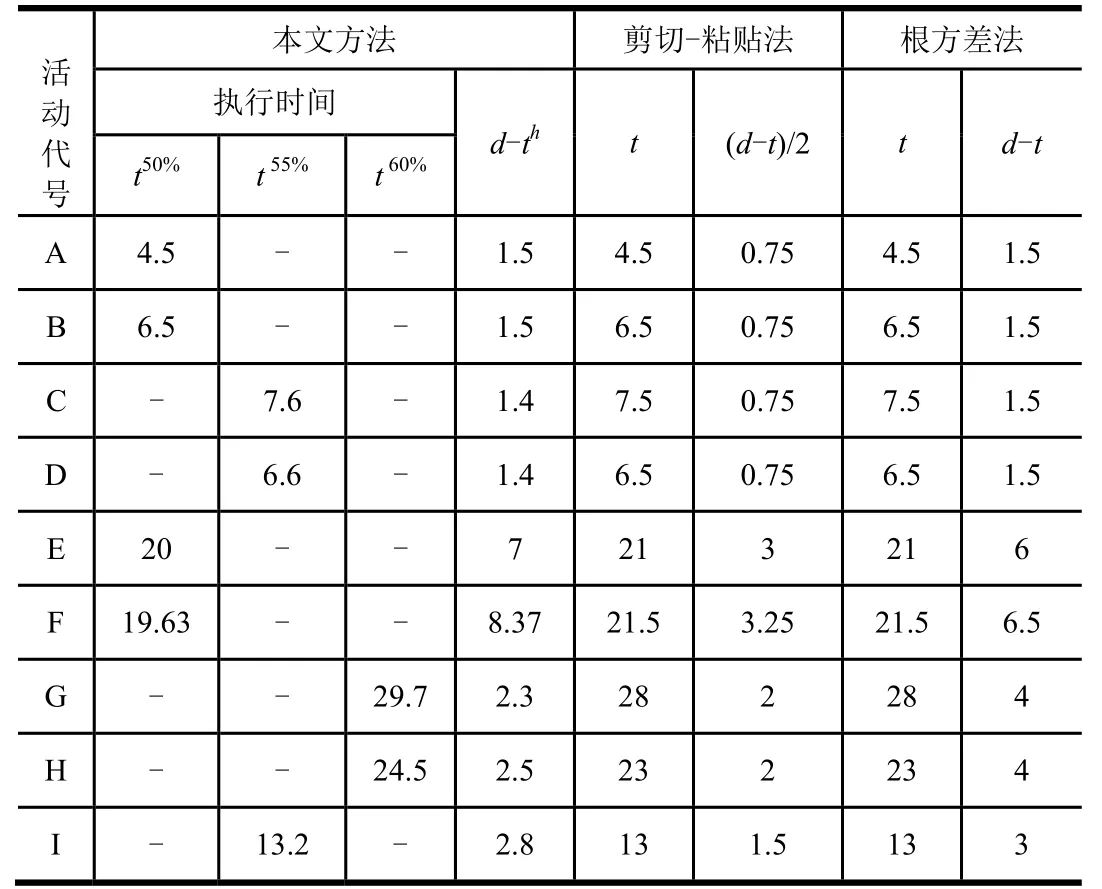
表3 各活动执行时间、安全时间裕量Tab.3 Execution Time and Safety Allowance of Activities
对比表3 中活动F、G、H 有关数据可见:当活动的估值范围(d~a)较大且不属于正态分布时,本文方法计算所得活动的执行时间、标准差明显不同于其他两种方法的计算值。其原因在于其他两种方法不考虑数据的分布特征。
算例中,由于活动C 与活动D 存在资源使用冲突,原并行执行关系转为了串行执行关系。以资源需求、供给为依据,根据活动的紧前关系、活动的执行时间,可寻得关键链与非关键链。此算例3 种不同计算方法所得关键链均相同,其甘特图如图6 所示,关键链为A-D-C-F-H-I,非关键链为B 及E-G。
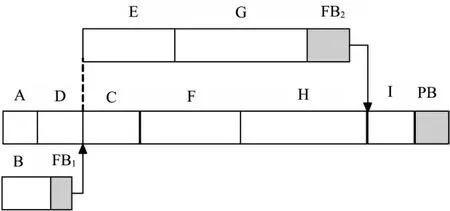
图6 算例关键链法甘特图Fig.6 Gantt Chart of the Example Based on Critical Chain
不同方法计算所得项目缓冲PB、汇入缓冲FB1、FB2以及项目完工时间如表4 所示。
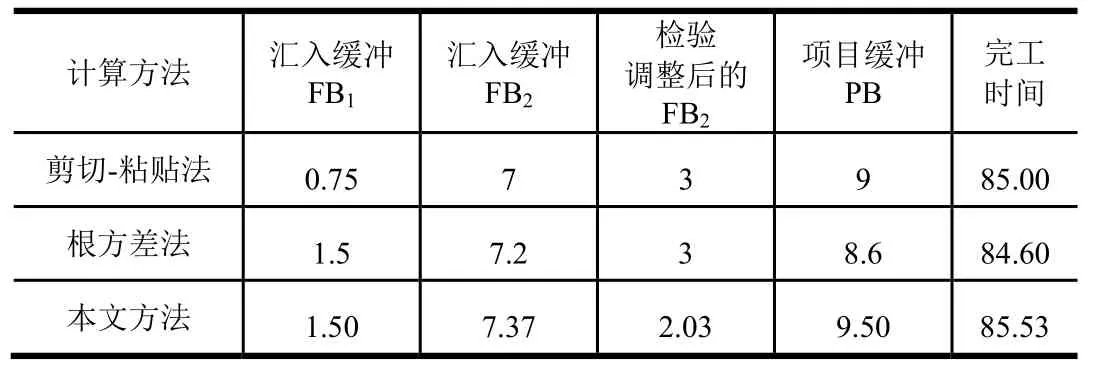
表4 不同方法计算所得缓冲区大小及完工时间Tab.4 Buffer Size and Completion Time Calculated by Different Methods
由表4 可知,3 种方法计算所得项目完工时间差别不显著,最大差距也仅为0.93 个时间单位;因此,本文所列方法既实现了关键链法的先进思想,也借助于真度值h 的灵活调整,使项目的各活动执行时间及各类缓冲区更符合实际。
3.3 完工时间模拟
本文应用Crystal Ball 软件,以各活动估计工期的概率密度为输入假设,进行算例完工时间模拟。
算例执行计划网络如图7 所示。由于资源约束,活动C 与活动D 之间增加了约束关系。
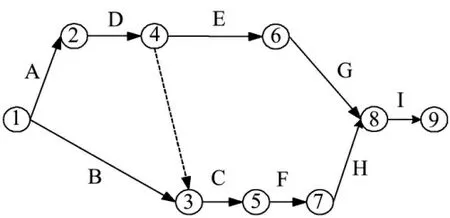
图7 算例关键链法计划网络Fig.7 Network Graph of the Example Based on Critical Chain
非关键链汇入关键链共有两个结点,由于输入数据为满足一定概率分布特征的随机数,故模拟过程中其紧后活动须满足限制条件式(13):
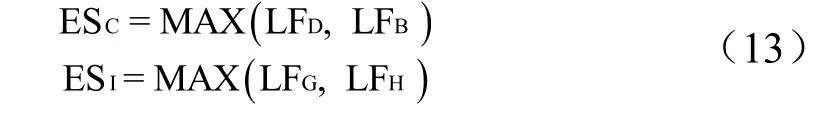
式中 ESC、ESI为关键链被汇入点紧后活动C、I 的最早开始时间;LFB、LFD分别为汇入节点紧前活动B、D的最晚结束时间;LFG、LFH分别为汇入节点紧前活动G、H 的最晚结束时间。模拟结果如图8、图9 所示。模拟结果显示:确定性为90%、95%时,项目完工时间分别为85.5、87.61 个时间单位。采用本文计算方法所得项目完工时间按计划完工的确定性达到90%,体现了关键链法的先进思想和作用。
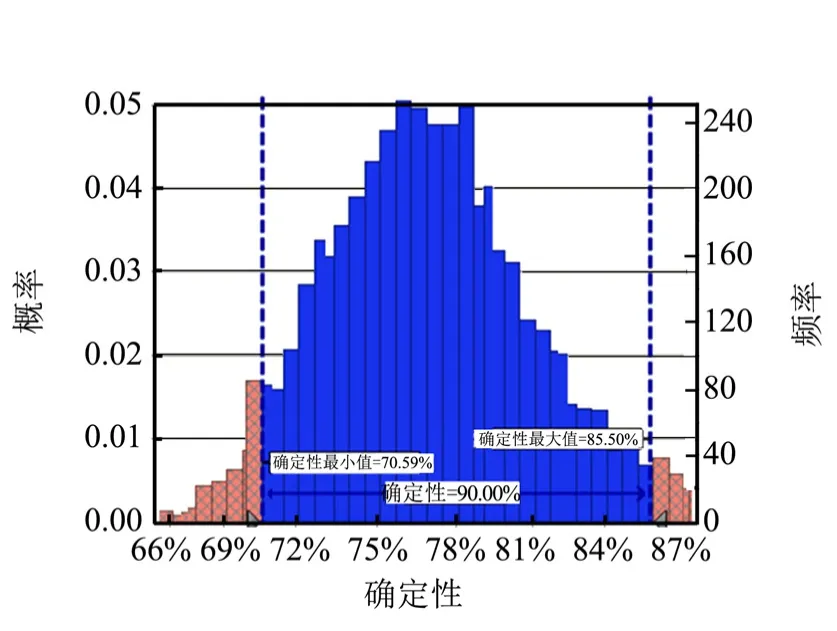
图8 完工时间模拟频率视图Fig.8 Simulation Frequency of Completion Time
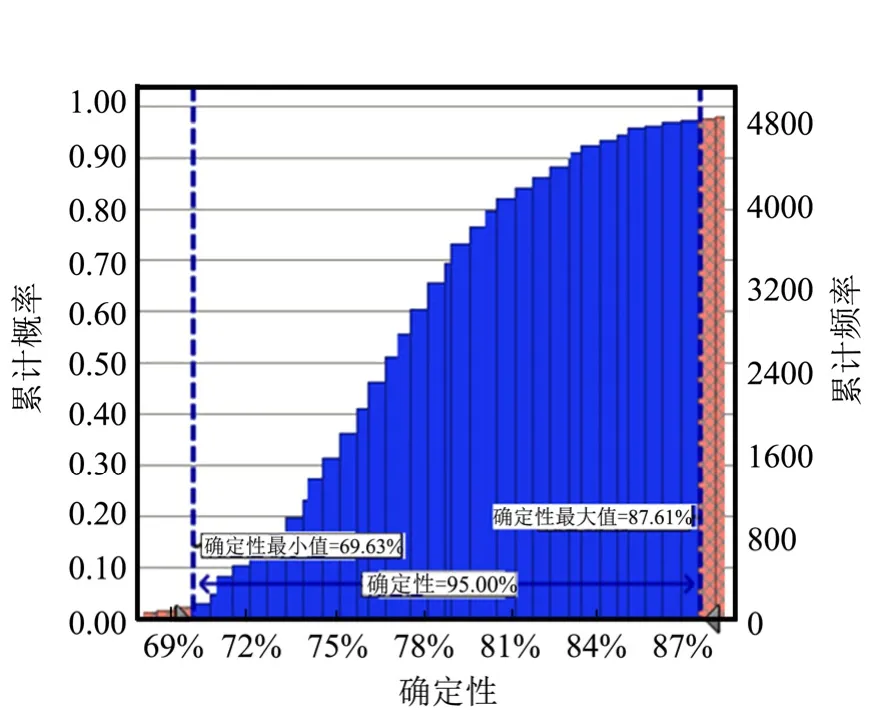
图9 完工时间累计频率视图Fig.9 Accumulation Frequency of Completion Time
4 结 论
a)将模糊数学引入活动工期估计,能较贴切地描述和处理工期估计的模糊性;同时采用梯形模糊数进行工期估计,也能体现航天项目不同类型活动的工期分布特征。
b)本文方法改变了僵化的执行时间确定方法,以不同真度值h 下的可靠工期th作为活动执行工期,有坚实的理论支撑。
c)项目管理人员可以充分利用人员经验和工期统计数据概率分布等知识,通过真度值h 取值的调整恰当地确定活动执行时间th、安全时间及缓冲区大小,从而使得编制的计划更加符合实际。
d)通过仿真模拟,应用该方法确定的缓冲区大小与项目计划,计划完工确定性可以达到较高水平,体现了关键链法的先进思想。
综上,本文提出的缓冲区大小确定方法,实现了初始设定的目标,具有一定的实用价值。
