基于频响比法的多维振动基础激励试验模态分析
2020-10-13张鹏飞吴家驹张永亮
张鹏飞,孙 颖,吴家驹,张永亮
(北京强度环境研究所,北京,100076)
0 引 言
结构动力学参数是航天器设计研制中重要的特性参数,可靠的动特性参数一般通过模态试验来获得。传统的模态试验中,使用力锤或者激振器对试验件进行力激励,通过测量激励力和响应加速度来计算频响函数,然后使用模态识别算法对频响函数进行识别得到结构的模态参数,目前该方法得到了广泛的应用[1]。但这种方法也存在一定不足,如当结构存在明显非线性时,其动力特性与试验量级高度相关,传统模态试验得到的频率阻尼特性与真实使用环境下的特性相差很大。
基础激励模态试验方法通过对试验件施加基础面激励形成分布载荷,利用试验件界面的运动参数识别边界约束条件下的模态参数。基础激励方法实际上是惯性力激振,激振力分布作用于结构,与试件真实使用环境的受力状态相似,所以从受力形式上来说,基础激励方法更符合实际。当结构存在强非线性时,基础激励方法可以通过施加真实环境振动得到更加可靠的模态特性。
文献[2]~[5]阐述了基础激励试验模态分析的方法,并用实例进行了验证,但都局限于单维振动激励的情况。产品的实际使用环境一般为多维振动环境。多维振动试验相对于单维振动试验,能够更真实的模拟产品的振动环境,激发出的振动响应更接近产品工作时的状态。但多维振动环境下结构模态识别面临新的问题,传递函数矩阵的估计需要避免各个自由度之间的相干影响导致的矩阵奇异。
本文深入研究多维振动基础激励模态分析试验方法,针对多维振动基础激励传递特性数据计算,提出了基于频响比的传递矩阵估计方法,解决了多维振动环境下传递矩阵获取的问题。设计典型试验对多维振动基础激励分析结果和传统力激励模态试验结果进行了对比,重点分析了多维振动基础激励模态结果反映出的结构频率和阻尼的非线性特征。
1 多维振动基础激励试验模态分析原理
运动基础激励试验模态分析的基本原理是,如果以运动基础作为参考坐标系,那么试验件受基础激励所产生的振动响应,相当于试验件与基础的连接界面固支,而结构上每个自由度被施加了一个大小与当地的质量和基础的振动有关的分布力[6]。
图1 为多维振动基础激励模态试验示意,试验件安装在六自由度试验台台面上。在固定坐标系下,试验台面的加速度为,试件响应的加速度为˙,试件与台面的相对加速度为,它们之间存在如下关系:

式中 G 为转换矩阵,包含6 列向量,即向量Gk,k=1,2,…,6,表示基础每个自由度的单位位移所造成的试件刚体位移,向量包含基础的3 个线运动分量和3 个角运动分量。

图1 多维振动基础激励模态试验示意Fig.1 Modal Analysis by Means of Multi-axis Base Excitation
基于线性理论和粘性阻尼假设,可以写出结构的运动微分方程:

式中 M,C,K 分别为试件的质量、阻尼和刚度矩阵。利用式(1)的运动关系可得:
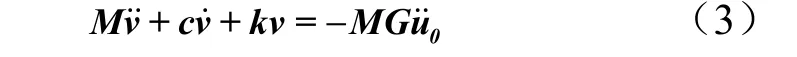
试件相对加速度与基础振动加速度之间的关系在频域有:
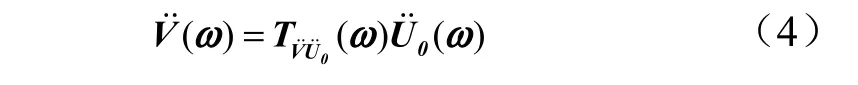
其中,传递率矩阵:
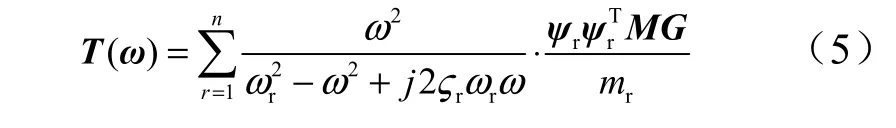
式中rω ,rς ,rψ 分别为第r 阶模态频率、模态阻尼比和振型,而 rm 为模态质量:

从式(5)可以看出,传递矩阵T(ω)是由标准的加速度比力的频响函数矩阵与质量阵M 和转换阵G 加权的频响函数和,所以可使用标准的模态估计算法来进行模态参数识别。传递矩阵可以从试验中测量出,从中可以识别出有效载荷边界约束状态的模态频率、阻尼比和振型。如果要获得模态质量,还需要引入有限元模型的质量矩阵,或者通过在试件与台面之间串入测力装置来测量界面力。
2 基于频响比的传递矩阵估计方法
获得传递矩阵T(ω)是进行频域法模态参数识别的基础。六自由度基础激励一般采用随机激励的形式,这种激励方式更接近试件的实际使用状态,能够更准确获得使用环境中的模态特性。常用的频响函数估计方法是响应比法[7]。首先在六自由度试验台上生成六自由度随机振动激励,并采集台面和试件上测点的响应˙˙u,然后解算出台面上的六自由度环境 ˙0˙u ,并根据式(1)计算出结构的相对运动˙˙v,那么传递率矩阵可直接算出
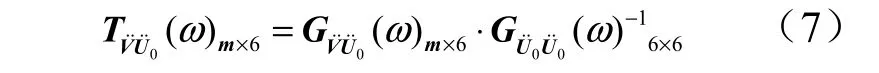
式中 GV˙˙U˙0(ω )和GU˙˙ 0U ˙˙0(ω )分别为输入和响应的互谱矩阵以及输入的自谱矩阵。
矩阵能够求逆的前提是矩阵 GU˙˙ 0U ˙˙0(ω )是正则矩阵,然而一般情况下,由于随机振动在结构传递的过程中相关性增强,即使将激振器的驱动信号设置为独立随机,六自由度激振系统加载台面的6 个振动方向也存在一定程度的耦合,例如加载台面的平动经常与转动相耦合。当六自由度振动输入之间不是完全线性独立时,矩阵 GU˙ 0U ˙˙0(ω )的条件数很大,求逆计算精度不高。
本文考虑到六自由度试验系统的激振原理,提出了基于频响比的传递矩阵估计方法。 e0为包含6 个激振器线性独立随机振动驱动信号的驱动向量,试件响应与驱动信号之间的关系在频域有
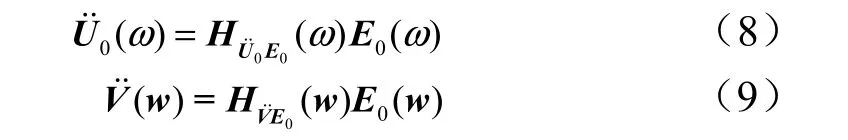
式中 H(ω)为响应对驱动的传递函数,可用谱矩阵的方法进行计算。传递率矩阵T(ω)可以这样估计:
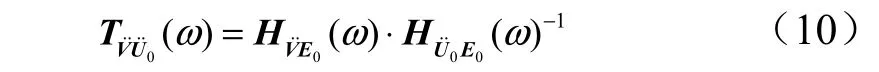
通过算例来说明式(7)和式(10)计算结果的区别。建立矩形截面梁的有限元模型,将梁划分为20 个单元,在梁根部同时施加不相干的线运动和角运动随机激励,求解端部节点1 到中部节点16 的角运动传递特性。虽然输入的线角激励不相干,但经过结构的传递,节点16 处的线角运动响应存在耦合。图2 显示了响应比法中需要求逆的矩阵 GU˙ 0U ˙˙0(ω )和频响比法中需要求逆的矩阵 HU˙0 E0(ω )在二范数下的条件数随频率的变化情况,后者的条件数远小于前者。图3 中将频响比法和响应比法计算的结果与理论值进行对比,可以看到基于频响比的传递矩阵估计方法得到的结果更接近理论值。
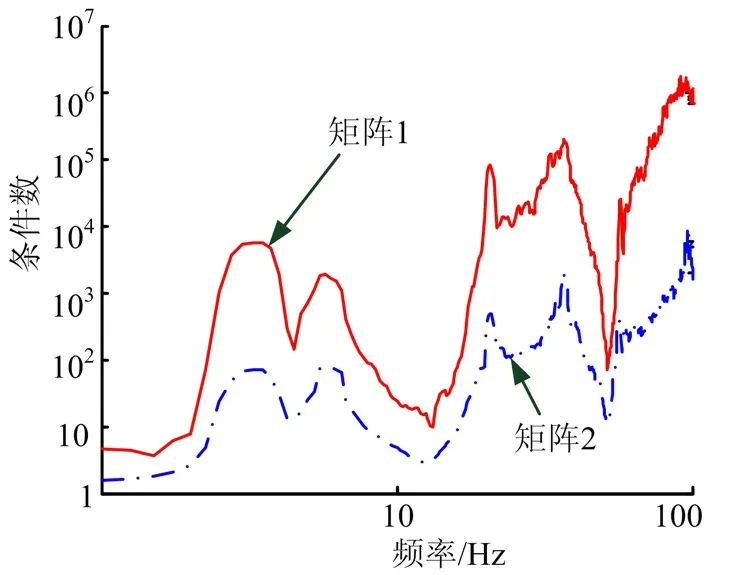
图2 矩阵条件数对比Fig.2 Compare of Condition Numbers
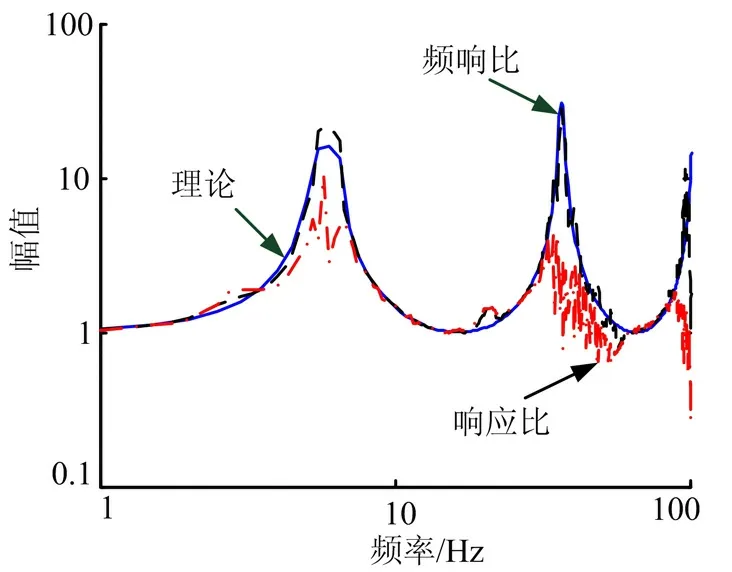
图3 传递率估计结果比较Fig.3 Compare of Estimate Results of Transmission Rate
3 试验研究
为了验证基于频响比的传递矩阵估计方法,发展多维振动环境中结构模态识别技术,进行了典型试验件的六自由度基础激励试验。试验激励设备为低频液压试验台,试验加载台面尺寸为2 m×2 m,由6 个液压作动器进行激励。试件为锥形结构,将试件底部通过转接工装连接在台面上,并在试件的一条母线上布置加速度传感器测点,试验系统组成见图4。
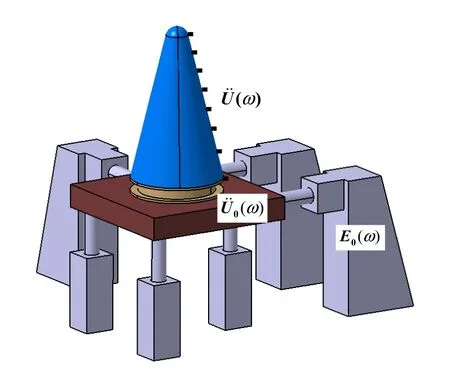
图4 试验系统组成Fig.4 Composition of Test System
对6 个液压激振器输入带宽1~80 Hz 的全不相干随机振动激励,在台面上产生六自由度运动,随机振动谱形见图5。按照基于频响比的传递矩阵估计方法,得到传递率矩阵T(ω)。图6 为试件顶部测点在Y、Z 方向的振动传递率曲线,能够清楚看到试验频带内存在2 阶共振频率,传递率曲线光滑无噪声,表明数据处理方法适用。
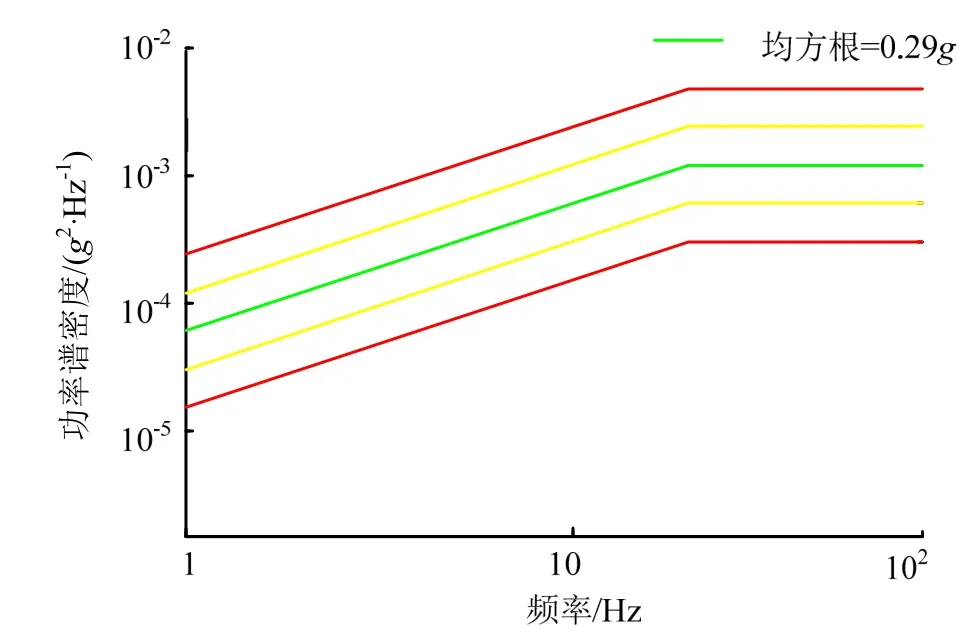
图5 随机振动功率谱Fig.5 Power Spectrum Density of Random Vibration
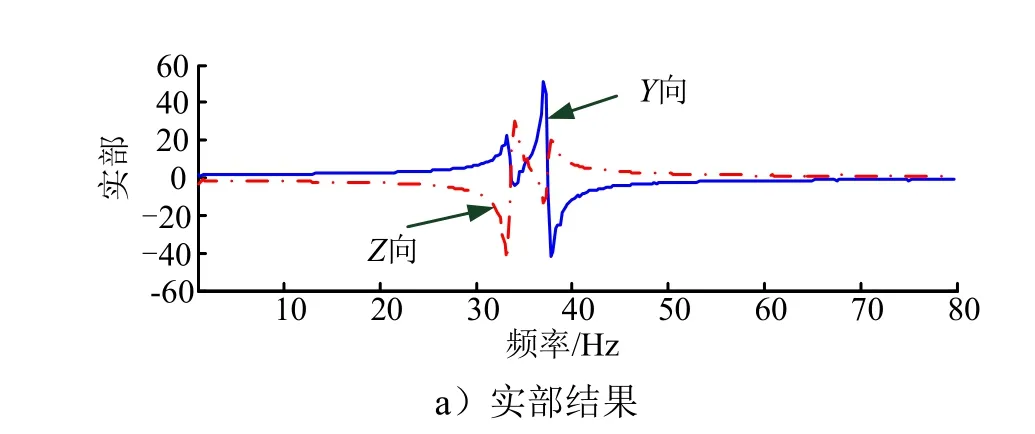
图6 传递率试验结果Fig6 Test Results of Transmission Rate

使用频域模态识别方法,识别出试件的频率、阻尼比和振型,识别出的试件在激振频率内的2 阶模态,结果见表1。为了便于比较,表1 列出了力激励固支边界模态试验结果,并使用振型相关系数表征两种试验方法识别出振型的相关性。可以看出,多维振动基础激励法与固支边界力激励法得到的模态振型一致性很好,但模态频率更低,阻尼比更大。这一结果符合多维振动基础激励模态试验的规律。多维振动基础激励试验将惯性激振力分布作用于结构,与力激励模态的点激励相比,结构受力更大,大部分金属结构具有渐软特性的非线性,因此频率更低。多维振动基础激励试验中结构振动位移大,产生的结构阻尼力更大,等效阻尼比也更大。

表1 模态试验结果Tab.1 Result of Modal Test
多维振动基础激励模态试验方法的优势还在于,对于大部分结构件,在材料、连接等环节存在多种非线性因素,使得结构的动态特性与环境振动量级高度相关[8],该试验方法能够获取模态特性与试验量级的相关性。在上述试验中,逐渐增大振动台的激振量级,分别按原试验条件的+3 dB 和+6 dB 量级进行振动加载和模态分析,模态频率和阻尼比识别结果随振动量级的变化见图7。
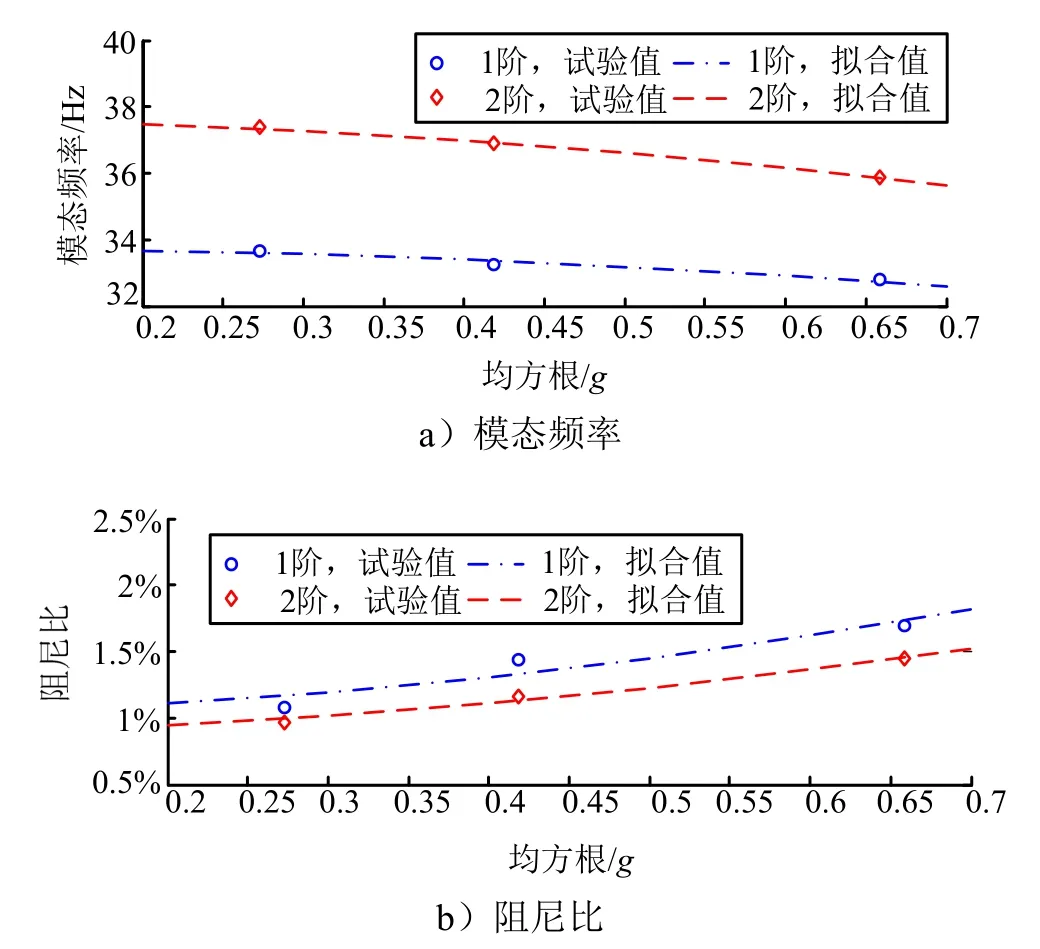
图7 模态频率与阻尼比的非线性特征Fig.7 Nonlinear Feature of Modal Frequency and Damping Ratio
随着振动量级的增大,模态频率逐渐降低,阻尼比逐渐增大,结构呈现出渐软刚度非线性特性。例如,1 阶模态频率降低了2.67%,阻尼比增加了57.31%。一般地,可以使用3 次多项式刚度和阻尼非线性模型对结构进行建模,对频率和阻尼结果进行拟合。结果表明,试验件的非线性特性基本符合3 次刚度和阻尼假设,多维振动基础激励模态试验方法能够很好的考核到模态特性的量级相关性。
4 结 论
a)本文提出基于多维振动基础激励的模态试验方法,获得试件固支边界下的模态特征,相比于力激励法和单维振动基础激励模态试验,多维振动基础激励法试件的试验边界和振动环境更接近其使用状态,获得的模态参数更接近实际工作状态。
b)在多维振动传递率的计算中,基于频响比的传递矩阵估计方法相对于响应比法,能够降低计算过程中矩阵的条件数,避免由于各个自由度之间的相干导致的矩阵奇异,从而获得高质量的传递矩阵。
c)对于非线性特性比较明显的结构,多维振动基础激励模态试验方法能够考核到试验件模态特性的量级相关性,有助于提高结构分析的精度。基于多维振动基础激励的模态试验方法能够得到更加可靠的试验结果,具有很好的实用价值和推广意义。
