一种简易RCS 系统姿态控制方法
2020-10-13马奥家李亚辉王辰琳
张 磊,马奥家,李亚辉,高 峰,王辰琳
(中国运载火箭技术研究院,北京,100076)
0 引 言
反作用力控制系统(Rejection Control System,RCS)通过对外喷射工质获得作用于飞行器上的反作用力矩,从而达到控制飞行器姿态的目的。RCS 系统产生的控制力矩相对较小,一般应用于在大气层外飞行或在稀薄大气中飞行的飞行器姿态控制中,具有不依赖外部使用环境、控制能力稳定等优点。
随着飞行器技术的不断发展,飞行器不断呈现出小型化的发展趋势,飞行器内部的装填空间变得越来越狭小。在满足飞行器姿态控制需求的前提下,如何降低RCS 系统的规模、降低对飞行器装填空间的需求成为了需解决的关键问题。
传统的RCS 系统为实现三通道姿态控制,采用8枚以上的姿控喷管[1~3],系统规模相对较大,对装填空间有较高要求。本文给出的一种简易的RCS 系统布局方案,采用4 枚姿控喷管布局,大幅降低了RCS 系统规模,同时,针对该布局存在的三通道耦合影响问题,提出了一种易于工程实现的姿控喷管开关逻辑策略,并设计了控制律,实现了三通道姿态的稳定控制。
1 RCS 姿态控制系统
本文给出的RCS 系统姿控喷管布局方案如图1 所示。4 枚姿控喷管安装于飞行器尾部某一平面上,姿控喷管向飞行器外侧喷射工质,反作用力方向指向飞行器内侧,推力作用线平行于象限间的45°线。
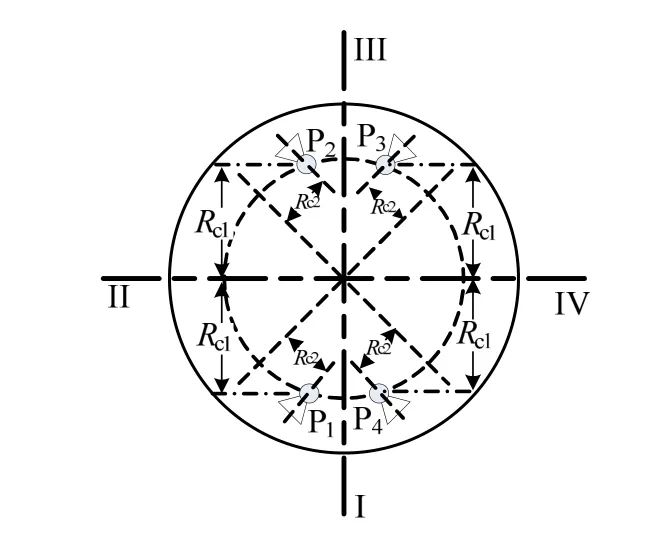
图1 RCS 系统喷管布局Fig.1 RCS System Nozzle Layout
同时打开任意两枚姿控喷管即可实现单通道姿态控制,共有6 种不同打开组合,分别与三通道独立控制时的6 种控制力矩方向需求相对应,可以实现三通道的独立姿态控制。当仅打开1 枚姿控喷管或同时打开3 枚姿控喷管时将产生三通道控制力矩,共有8 种不同的打开组合,分别与三通道同时控制时的共8 种控制力矩方向需求相对应,可以实现三通道的姿态控制。
喷管开关组合与控制力矩方向对应关系如表1 所示(4 枚喷管同时打开时不产生控制力矩,与喷管全部关闭时力矩相同,表格中不重复列出)。俯仰、偏航和滚动三通道的控制力矩需求组合共有27 种,而本文的姿控喷管布局方案仅能产生15 种不同的力矩组合形式,无法产生的12 种力矩组合为双通道有控制力矩需求时的组合。因此,在进行双通道姿态控制时,或是仅进行单通道姿态控制,暂时不对另一通道进行控制,或是产生三通道的控制力矩,实现双通道控制的同时不可避免的引入了对另一通道的耦合干扰。
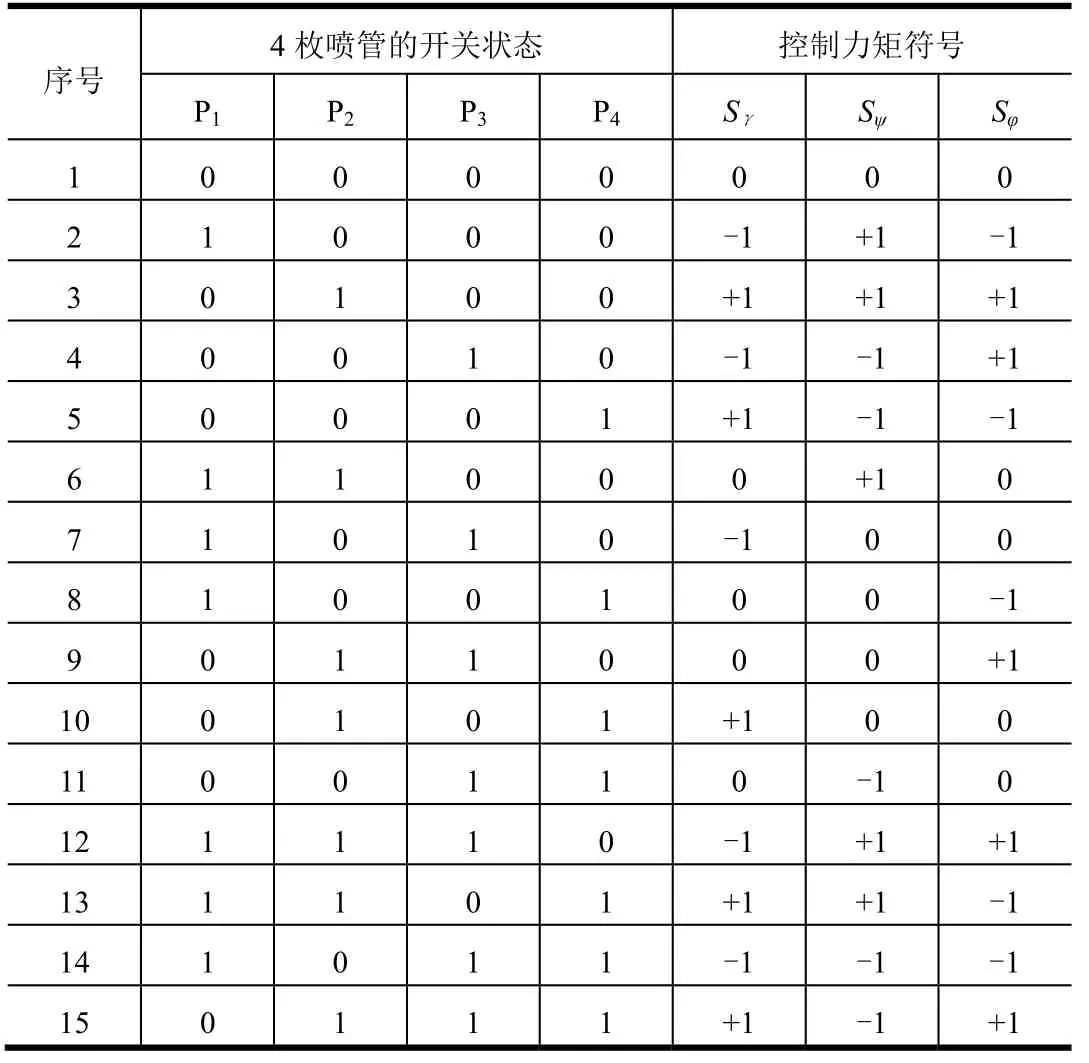
表1 喷管开关组合与控制力矩对照表Tab.1 The Comparison Table of Switch Combinations and Control Moment
2 RCS 系统姿态控制方案
2.1 控制率设计
采用极限环进行姿态控制[4,5],以俯仰通道为例,控制指令计算方法如式(1)所示。俯仰、偏航和滚动通道控制指令分别用Kφ、Kψ和Kγ表示。当控制指令为-1 时,表示该通道有负向控制力矩需求;为1 时表示有正向控制力矩需求;为0 时表示没有控制力矩需求。控制特性示意如图2 所示。
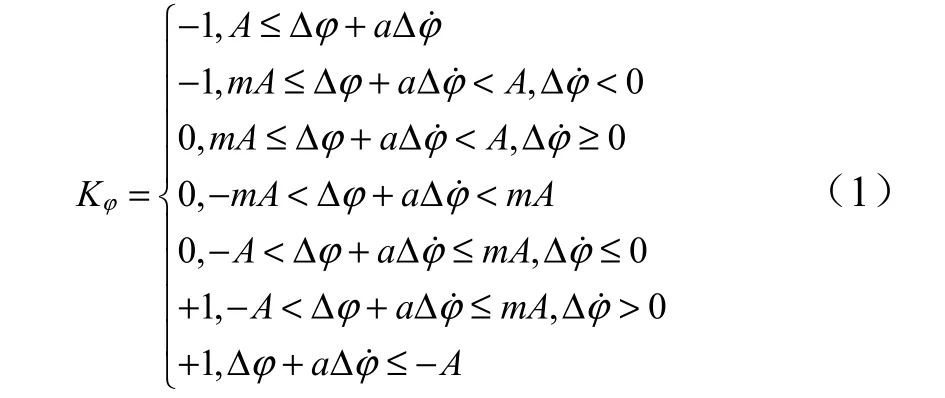
式中 m 为回环系数;A 为控制门限;a 为动态增益;ϕ为俯仰角; ϕΔ 为俯仰角偏差; ϕ˙Δ 为俯仰角速度。
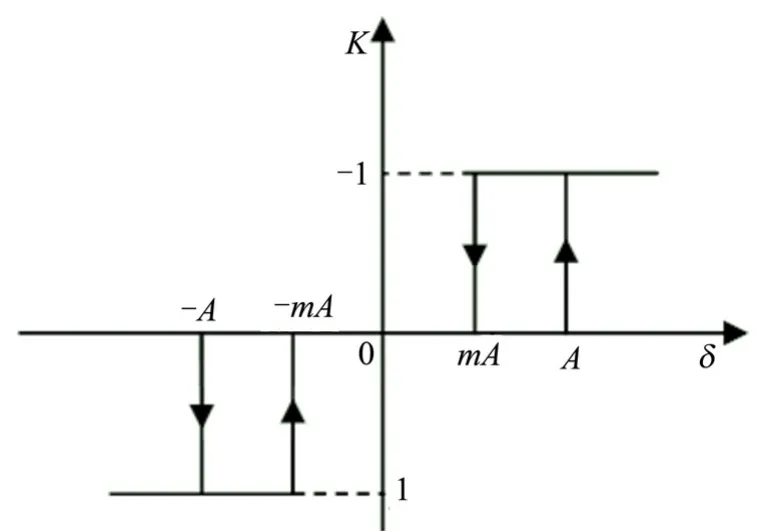
图2 控制特性示意Fig.2 Schematic Diagram of Control Characteristic
2.2 姿控喷管开关逻辑
在上述姿控喷管布局的基础上,制定姿控喷管开关逻辑时的主要策略如下:
a)单通道控制和三通道控制时,不存在通道间耦合影响,根据控制力矩需求直接分配姿控喷管产生相应的控制力矩;
b)在进行双通道控制时,引入三通道的控制力矩进行姿态控制。在实现双通道控制的同时,引入了对另一通道的干扰;
c)双通道的控制力需求均与两组三通道控制力矩需求相对应(如Kφ=Kψ=1时,对应Kφ=Kψ=Kγ=1和Kφ=Kψ=1,Kγ=-1 两种情况),在使用时遵循喷管使用最少原则,选择仅开启1枚喷管的开关逻辑来实现双通道的控制。
根据以上控制策略确定喷管开关逻辑如表2所示。
采用以上开关逻辑进行姿态控制,虽然在进行双通道控制时引入了对另一通道的干扰,但飞行器姿态在控制力矩和干扰力矩的双重作用下将逐渐转化为三通道姿态控制或单通道姿态控制问题,最终实现飞行器姿态的动态稳定。下文的仿真结果也证明了这一点。
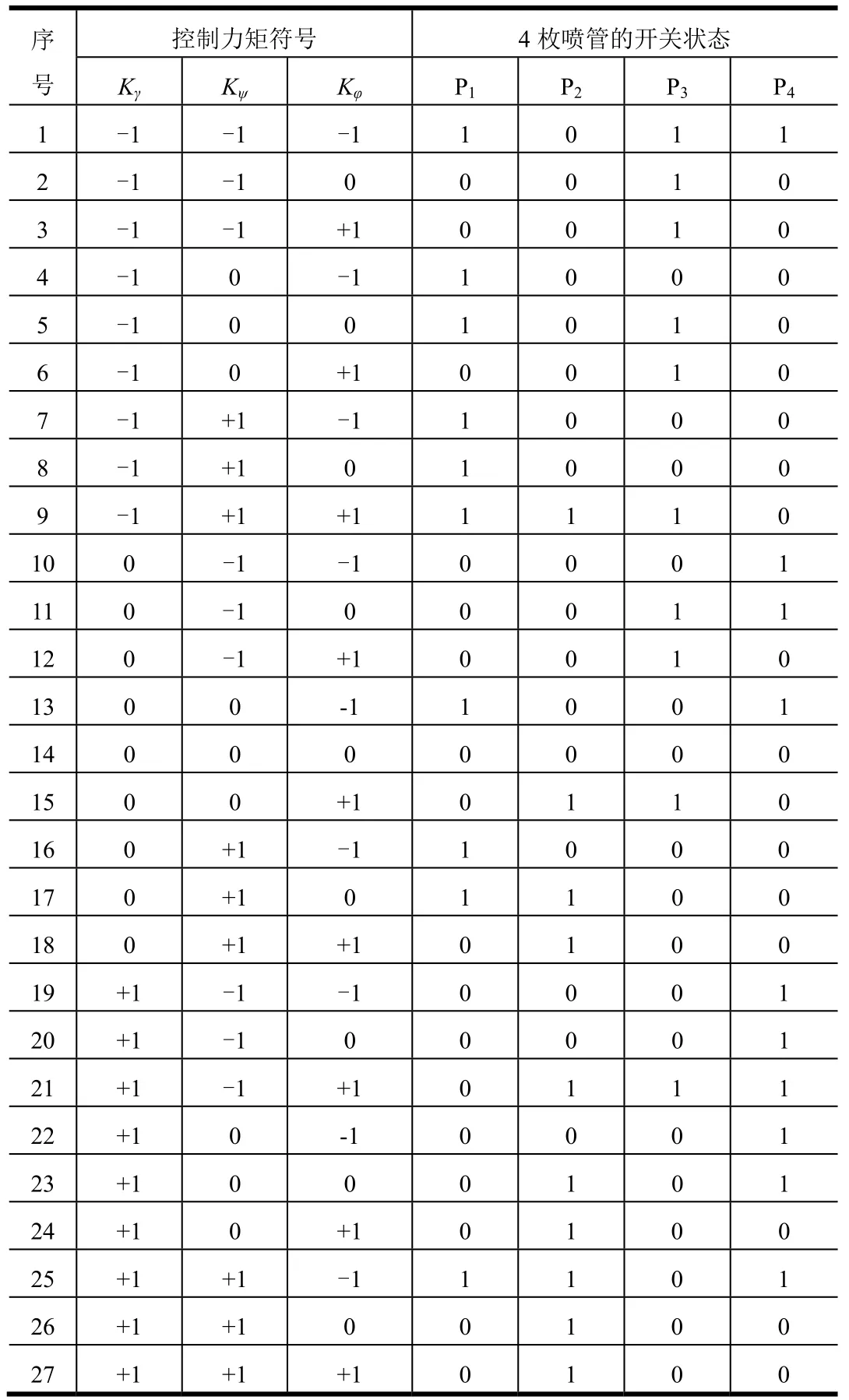
表2 姿控喷管开关逻辑表Tab.2 Switch Logic of the Attitude Control Nozzles
2.3 动力学模型
由于RCS 系统主要工作于稀薄大气或是大气层外飞行时段,因此忽略了大气等外部飞行环境影响。并且RCS 系统姿控喷管产生的推力量级较小且为断续作用,对飞行器质心运动的影响很小,因而在进行仿真分析时忽略了质心运动的影响,仅分析飞行器姿态的稳定性。飞行器动力学模型为[6~8]

式中 ϕ,ψ ,γ 分别为俯仰角、偏航角和滚转角;x1ω ,ωy1,ωz1分别为俯仰、偏航和滚转角速度; Jx, Jy, Jz为转动惯量;Mcx1,Mcy1,Mcz1为三通道控制力矩;Mdx1,Mdy1,Mdz1分别为三通道干扰力矩。
以仅打开喷管1 为例,产生的三通道控制力矩计算公式如下:
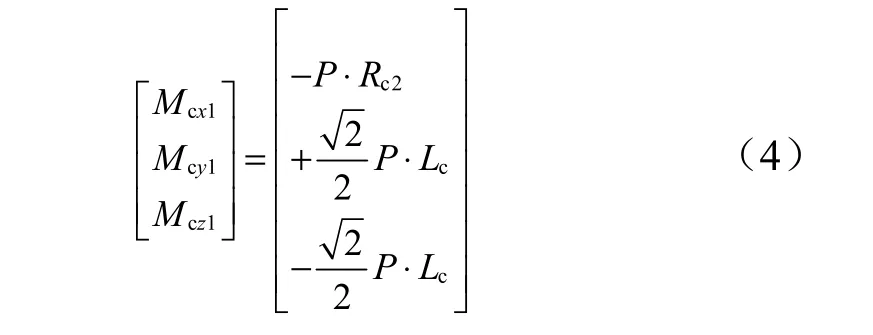
式中 Lc为姿控喷管在俯仰、偏航通道上的作用力臂;Rc2为姿控喷管在滚动通道上的作用力臂;P 为单个喷管的推力。喷管力臂示意见图1。
定义:P·Rc2=Mr,P· Lc=M,式(4)可以表示为
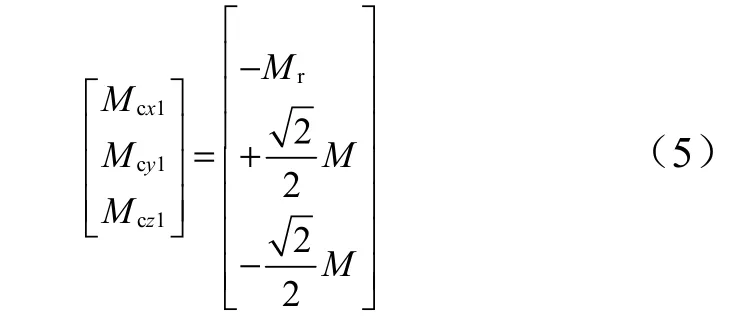
式中 Mr为单位滚动通道控制力矩;M 为单位俯仰、偏航通道控制力矩。
定义:Mcx1/Mr=,Mcy1/M=,Mcz1/M=。则当仅打开喷管1 时,通道等效控制指令为
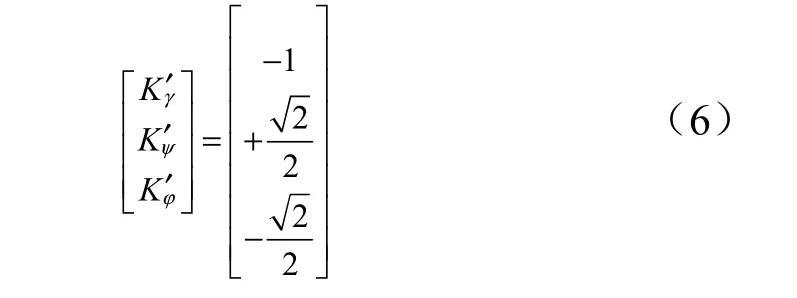
其他喷管打开时的等效控制指令计算方式与喷管1类似,因此也能够得到多个喷管同时打开时的等效控制指令,可以据此分析姿控喷管的解耦状态。
3 仿真分析
3.1 仿真条件
为验证姿态控制方案的有效性设计了仿真算例。姿态控制系统跟踪姿态指令,俯仰、偏航通道包括姿态调整及姿态保持等指令,滚动通道为姿态保持指令。
仿真时飞行器初始参数如表3 所示。
由于存在姿控喷管推力偏斜等干扰因素,在仿真中需要引入对应的干扰力矩。为引入简便且达到贴近真实工况的目的,在进行单通道控制时,在另外两个通道同时产生通道控制力矩1%的干扰力矩,以进行俯仰通道控制为例,在偏航通道将产生0.3 N·m 的干扰力矩,滚动通道将产生0.03 N·m 的干扰力矩。在进行三通道或双通道控制时,由于三通道均产生了控制力矩,作为小量的干扰力矩则可以忽略。
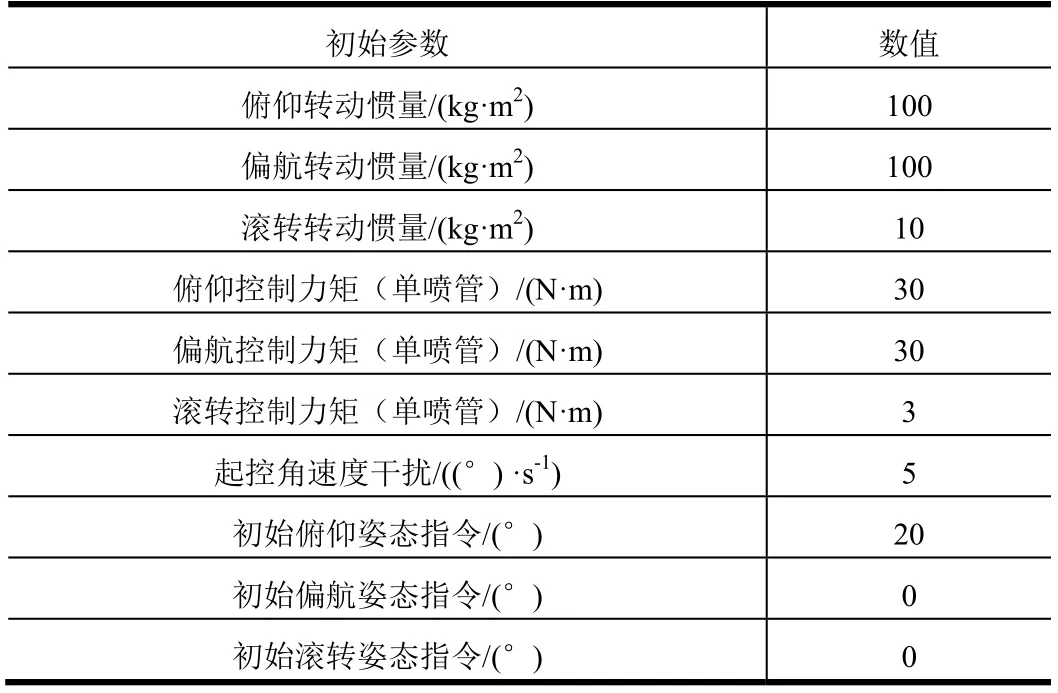
表3 仿真初始条件Tab.3 The Initial Condition of Simulation
3.2 仿真结果
采用上文所述的动力学模型、姿态控制方案和仿真初始条件,完成了控制参数设计和仿真分析。
图3、图4 为三通道姿态跟踪曲线。
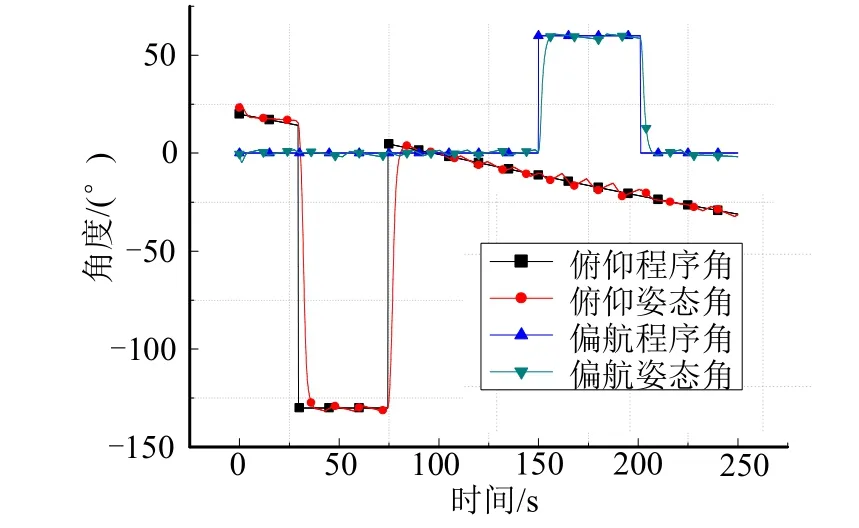
图3 俯仰、偏航姿态角跟踪曲线Fig.3 Tracking Curve of Pitch and Yaw Attitude Angle
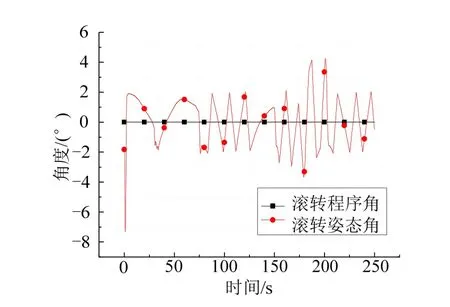
图4 滚转角跟踪曲线Fig.4 Tracking Curve of Roll Angle
由图3 和图4 可以看出在姿态稳定段和姿态调整段均能保证姿态稳定,同时在姿态调整时有很好的跟踪效果。
仿真部分时段的三通道等效姿态控制指令如图5所示。从图5 中可以看出,在进行多通道控制时,本文给出的姿控喷管开关逻辑工作正常,在出现通道耦合时,姿控系统有效的对姿态控制指令进行了解耦,实现了三通道稳定控制。
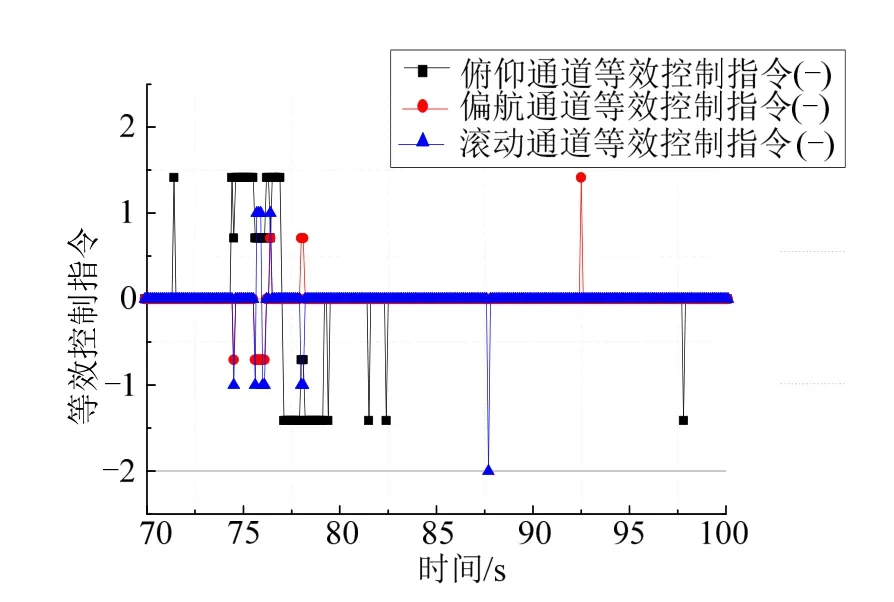
图5 等效姿态控制指令Fig.5 Equivalent Attitude Control Command
4 结 论
在保证三通道稳定控制的前提下,本文给出了一种新型RCS 系统姿控喷管布局方案,有效地对RCS系统进行了简化。针对该布局存在的双通道控制时无法完全解耦问题,给出了一种易于工程应用的姿控喷管开关逻辑策略并设计了控制律,有效实现了三通道姿态稳定控制。通过数学仿真分析证明了姿控喷管布局方案和开关控制逻辑的有效性。
