最近公共祖先算法在管道运输的应用

黄检宝，彭诗怡，郭煜锐

（南华大学，衡阳421001）

0 引言

国家发改委在2017 年1 月19 日，引发了《十三五规划》，我国管道运输的总里程增量十分巨大[1]，在互联网大数据时代背景下，如何用智能算法监控管道运输显得尤为重要。最近公共祖先算法是图论的经典算法，它能够快速地找出树中两点的最近公共祖先[2-3]，相对于朴素的暴力搜索算法，其有较低的时间复杂度，本文通过最近公共祖先算法实现了快速监控管道网络中的最大流量，保障了管道运输的安全。

1 最近公共祖先算法

1.1 概述

对于有根树T，结点u 和v 的最近公共祖先为LCA(u,v) ，LCA(u,v) 满足为u和v的深度最大的父结点。例如，存在树T0，其点集为V{1,2,3,4,5,6}，边集为E{(1,2),(1,3),(2,4),(2,5),(5,6)} ，令根结点为1，如图1 所示，结点4 和结点6 的公共祖先有结点1 和结点2，由于结点2 的深度比结点1 的深度大，所以结点2 是结点4 和结点6 的最近公共祖先。

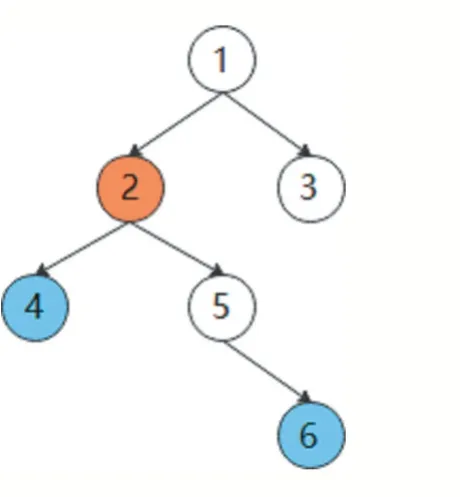
图1 示例图（一）

最近公共祖先问题的算法，主要包括欧拉序结合ST 表法、倍增法[3]、并查集[2-3]结合Tarjan 算法[4]和树链剖分法[2]。其中包括离线算法和在线算法，离线算法需要提前知道所有要求LCA 的点对{(ui),vi,…}，再一次性处理，得到所有的点对的公共祖先；而在线算法可以合理的根据需求，每输入一对u 和v，即可求出他们的LCA。这四种算法中，除了并查集结合Tarjan 算法为离线算法，其他都是在线算法。欧拉序结合ST 表法的核心思想是首先通过深度优先搜索得到有根树的欧拉序，然后通过ST 表不断查询两点的LCA；倍增法的核心思想是，将两点同时往根节点跳跃2 的指数倍，当深度差相等时，即可得到两点的LCA；并查集结合Tarjan算法的核心思想为，在深度优先搜索返回的过程中，不断的用并查集合并搜索到的点，LCA 为并查集根节点。树链剖分的核心思想为，将树划分为轻重链，然后用线段树或者树状数组来维护每一条链，LCA 即为数据结构查询得到的结果。

1.2 欧拉序和ST表

最近公共祖先问题，包括四大算法，有线算法更具有实际应用价值，下面对欧拉序和ST 表法求LCA 进行详细介绍。

欧拉序是对图搜索过程中，记录搜索路径中遍历的结点，每次经过的点都需要记录。与dfs 序不同的是，dfs 序类似于前序遍历，只是将第一次遍历的点按顺序记录下来。以图1 为例，欧拉序为：{1，2，4，2，5，6，5，2，1，3，1}，dfs 序为：{1，2，4，5，6，3}。

ST 表是一种能实现快速查找区间最大值或者最小值的数据结构，它通过二的幂次方来划分区间，不断的利用上一个小区间，合并求出当前大区间的最大值或者最小值，而查询时只需要将查询的区间划分为尽可能大的二次幂区间，重叠覆盖取其最大值或最小值即可得到结果。

将这两个算法结合，首先遍历树得到欧拉序，然后在欧拉序中使用ST 表快速查找LCA，例如，在图1 中，求结点4 和结点6 的最近公共祖先，在欧拉序中找到结点4 和结点6 第一次出现的位置，即第3 个和第6个，对应的序列为{4，2，5，6}，再利用ST 表查询第3 个位置和第6 个位置之间的最小值，即LCA 为{4，2，5，6}的最小值，结果是结点2。

2 管道运输问题

A 国建立了一个庞大的石油管道运输网络，如何才能快速的监控管道网络的流量，来保障石油运输过程中的安全性呢？A 国有N 个城市，为了节省管道的材料费，A 国只布置了N-1 条石油运输管道，即刚好能保证两两城市之间能互通，没有城市是孤立状态。现在A 国管道运输管理者经常需要增加某两个城市之间的石油流量，假设每增加1 单位流量，两城市之间的管道也会增加1 单位压力，经过多次操作后，A 国整个管道网络最大的压力是多少？

算法的输入格式为：第一行输入整型N，代表A 国城市的数量，之后输入N-1 行整型ai和bi之，代表城市ai和城市bi之间有一条管道连通，再输入整型k 代表需要对管道网络进行k 次操作，输入k 行aj，bj和cj，分别代表城市aj和城市bj经过的管道流量增加cj单位。（2≤N≤50000，1≤k≤100000）

算法的输出格式为：输出一行整型数据，即整个管道网络的最大压力。

3 算法分析与设计

3.1 问题简化

A 国的管道运输网络看做一个无向图，有N 个点、N-1 条边，两两点之间刚好相互可达，那么这个无向图不存在环，因此它也是无根树。对无根树T1中某些路径经过k 次增流，每次增流相当于增加边权，最终需要求k 次增流后的最大边的权值是多少。下面，通过LCA 和树上标记算法来解决这个问题，并分析为什么树上差分不可以有效地解决此问题。

3.2 数列区间操作

（1）数列差分

数列区间操作常用的方法为数列差分[3]，从数列差分的角度进行推广，对树链操作，因此想到树上差分，下面先介绍数列差分。数列差分可以做到批量操作数列区间加减法或者乘除法，适用于需要多次操作区间的情况。与枚举算法对比，枚举算法每次操作需要遍历区间，时间复杂度为O（n2)，而数列差分只需要将需要操作的端点标记即可，最后遍历一遍数列即可得到最终的结果，时间复杂度为O（n）。

例如，存在数列{1，5，6，2，5，5}，分别对区间[0，4]、[1，5]的每个数加1，首先计算出差分数组d={1，4，1，-4，3，0，0}，然后处理端点，对于区间[0，4]，将d[0]++，d[4+1]--，对于区间[1，5]，d[1]++，d[5+1]--，最终d={2，5，1，-4，3，-1，-1}，之后求d 数列的前缀和，即为最终答案：d={2，7，8，4，7，6}（答案只取前六个数）。

（2）数列标记

同样是对数列区间操作，不使用到差分，只对区间端点标记，也可以在O（n）时间复杂度下解决问题。同样在上一个例子的基础上，设标记数组为flag={0，0，0，0，0，0，0}，若[0，4]、[1，5]每个数都加1，则flag[0]++、flag[4+1]--、flag[1]++、flag[5+1]--，flag={1，1，0，0，0，-1，-1}，flag 前缀和为s={1，2，2，2，2，1，0}，这个数列就是原数列每个数的增量，因此，最终结果为{1+1，5+2，6+2，2+2，5+2，5+1}，即{2，7，8，4，7，6}。

3.3 LCA求解管道运输问题

（1）LCA 与树上差分

类比数列差分，结合LCA 做树上差分，能做到多次操作某一条链的权值。假设根节点为结点1，dis[i]代表结点i 前向边的差分流量，从结点1 开始遍历，首先求出初始的dis 数列，之后，若对结点aj到结点bj中每一条边加cj，因为涉及到操作LCA（aj，bj）的子结点，且又无法直接判断LCA（aj，bj）的子结点，是否在结点aj到结点bj的路径上，因此需要对结点aj到结点bj的路径搜索。

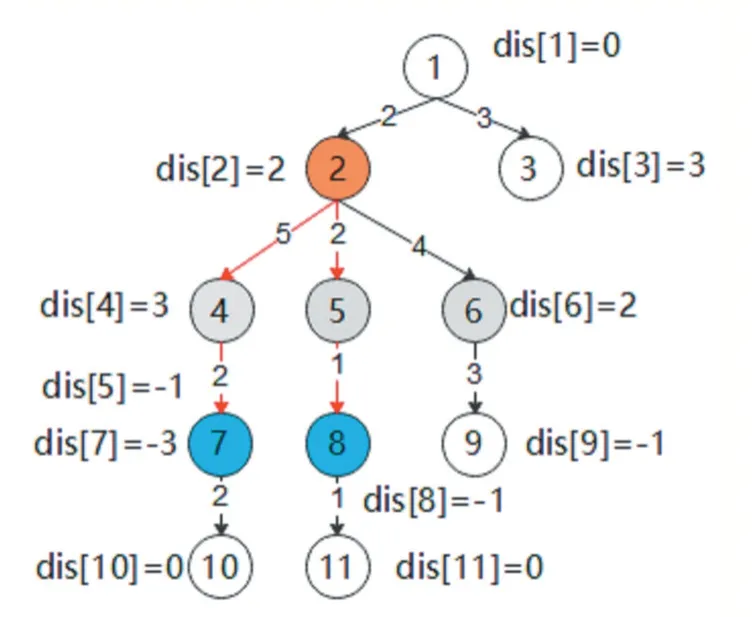
图2 示例图（二）

如图2 所示，对结点7 和结点8 的路径权值都增加1，LCA(7,8)为结点2，因为结点4 和结点5 在路径之上，并且为结点2 的子结点，因此dis[4]++，dis[5]++，对结点7 和结点8 的子结点操作，dis[10]--，dis[11]--，最后从结点1 开始求一遍前缀和即可。（这里在确定结点4 和结点5 时，则需要对结点7 到结点8 的路径搜索。）

时间复杂度分析：k 次询问，每次都需要对路径进行搜索，为O（n），所以总的复杂度为O（kn），与朴素的暴力搜索算法时间复杂度一致，因为用到了LCA 和其他的处理，因此时间复杂度常数会更大，总的来说还不如暴力搜索法。

（1）LCA 与树上标记

将根结点作为参考点，此时将dis[i]定义为结点i到根结点路径上边的增量，pre[i]定义为结点i 的前向边权，若对结点aj到结点bj中每一条边加cj，则dis[aj]+=cj，dis[bj]+=cj，dis[LCA（aj，bj）]-=cj，最后后序遍历树T1，原始的边的权值加上dis 的增量和，即为操作k 次后的边权结果，并求出边权的最大值即为问题结果。

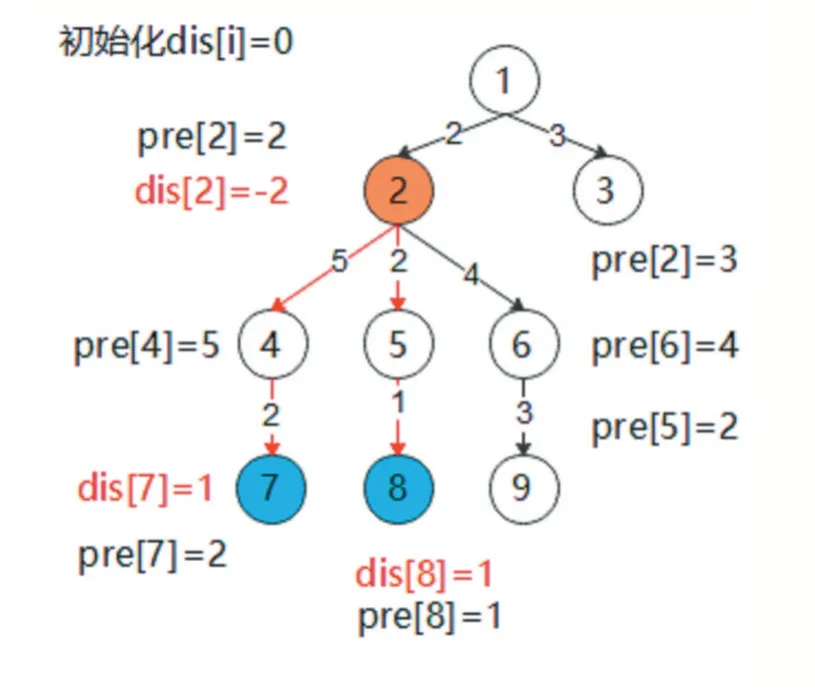
图3 示例图（三）

如图3 所示，对结点7 和结点8 的路径权值都增加1，dis[7]++，dis[8]++，dis[2]-=2，计算dis 从叶子结点到根节点的累积增量，从结点7 至结点1，从结点8 至结点1，dis[7]=1，dis[4]=1，dis[8]=1，dis[5]=1，dis[2]=dis[4]+dis[5]+dis[2]=0，最终pre[i]+=dis[i]为最终结果。

算法复杂度分析：LCA 使用欧拉序结合ST 表的方法，ST 表预处理的时间复杂度为O（nlog2n），查找的复杂度为O（1），树链操作都转化为标记，最后只需要遍历求出累积值即可，时间复杂度为O（n），所以整个算法时间复杂度为O（nlog2n）。

4 结语

本文分析了欧拉序、ST 表、数列区间问题和树上路径问题，结合欧拉序和ST 表能求出树上两结点的最近公共祖先，再以根节点为参考进行树上标记，能在O（nlog2n）的时间复杂度下，求解出了管道网络的最大压力，而暴力搜索算法和树上差分算法的复杂度为O（kn），由此可知在需要查询的次数k 较多时，本文提出的最近公共祖先和树上标记算法，能大大节省计算资源，在管道运输监控上具有较大价值。