改进蚁群算法在TSP 问题中的应用

徐书扬，王海江

（浙江科技学院，杭州310023）

0 引言

蚁群算法是一种于1992 年由文献[1]用于寻找最优路径的经典概率型算法。与其他启发式算法相比，蚁群算法具有良好的鲁棒性（可改进方向多，适用于多种问题的解决）以及优越的全局搜索能力（蚁群算法往往以全局最优为目标解决问题）。因此，蚁群算法在多个领域中得以应用，例如：区域建设[2]、路径规划[3-6]、影像测量[7]、调度管理[8-9]等。然而，蚁群算法也同样存在一些不足之处，例如：在处理信息量较大的问题时迭代速度过慢，算法易陷入局部最优而错过最优解，对参数的设置有很高的要求，错误的参数设置容易导致结果误差过大等[10-11]。

针对传统蚁群算法存在的问题，不少学者提出蚁群算法的改进方案来解决蚁群算法本身的缺陷。例如，在TSP（Traveling Salesman Problem）问题的解决中，黄泽斌[12]曾提出利用K-近邻分区方法对大规模TSP问题进行聚类分区，然后利用蚁群算法对每个子区域进行最优化求解，最后再将连接这些子区域之间距离最近的点连接起来实现TSP 问题的求解，该算法相较于传统算法有更快的收敛速度，并且在处理信息量较大的图中有更小的算法复杂度，节约了解决问题的时间成本。但是，连接两个子区域的方式为寻找子区域之间距离最近的点将其相连，意味着连接两个子区域之间的路径有且仅有一条，从而降低了算法探寻更优路径的可能性，使得结果易产生较大的偏差。在点与点的路径规划问题中俞烨[13]曾提出启发式因子的改进方案，该方案令启发式因子既考虑到下一步距离最近的结点，也考虑到下一步所到结点距离终点的距离，从而在图像信息量较小时一定程度上避免了算法陷入局部最优，也加快了算法初期的收敛速度。但是这样的改进策略仅适用于信息量较小的图，当图中信息量较大时，对下一结点到终点距离的考虑反而会是干扰算法收敛的因素。Stützle T[14]曾提出最大-最小蚁群系统的概念，在每次迭代中仅更新最优路径上的信息素，此方法加快了算法收敛的速度，但是同时也增大了算法陷入局部最优的可能。

上述算法一定程度上解决了蚁群算法的种种弊端，在某一特定场合下比起传统蚁群算法有着更好的适用性。但是在非特定情况下或多或少存在一些弊端。本文以TSP 问题的讨论为基，对蚁群算法做出改进，以全局最优为目标，降低结果陷入局部最优的概率，提高蚁群算法求解结果的精确度。在本问题的讨论中，苏晓琴[15]曾提出根据时间的推进改进信息迭代方案，使得算法能更快的收敛，这样的改进一定程度上能提高算法的求解精度，但是依旧未能解决算法易陷入局部最优的情况。黄泽斌[12]曾提出用近邻分区的方法来提高算法的求解精度，但是这样的方法仅适用于大规模求解TSP 问题。在TSP 问题的解决中上述算法相较于传统蚁群算法有着明显的优势，但是，仍未解决蚁群算法的一大弊端：易陷入局部最优。本文提出一种蚁群算法的改进方案，使得算法能一定程度上避免陷入局部最优的情况，提高算法整体的求解精度。

1 TSP问题和蚁群算法

1.1 TSP问题的描述

TSP 问题又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。它描述了以下场景：有一名旅行商人要拜访各个城市，城市的数量为n，限制条件为每个城市仅拜访一次且所有城市必须都需要拜访，优化目标为使得在拜访完所有城市并最终回到起点的情况下旅行商人走过的总路径长度最短。经典的TSP 问题中点与点之间的路径长度为点与点之间的直线距离。本文将改进后的蚁群算法应用于TSP 问题的解决中，减少蚁群算法易陷入局部最优的情况，使得TSP 问题的求解有更高的精确度。

1.2 蚁群算法的描述

蚁群算法的思想来源于自然界蚂蚁觅食，蚂蚁在寻找食物源时，会在路径上留下蚂蚁独有的路径标识——信息素，蚂蚁会感知其他蚂蚁在各条路径上留下的信息素，并根据各条路径上的信息素浓度来选择之后要走的路，路径上留有的信息浓度越高，则蚂蚁更倾向于选择该路径。在蚂蚁选择某条路径后也会在改路径上留下信息素吸引更多蚂蚁选择该路径，随着时间的推移，信息素浓度不断增大，蚂蚁选择路径的概率也随之增高，由此形成了正反馈机制。由于蚁群算法的正反馈性，因此蚁群算法也属于增强型学习算法的其中一种。

对于TSP 问题，设蚁群中蚂蚁的数量为m，结点的数量为n，结点i 与结点j 之间的欧式距离为dij(t)，t 时刻结点i 与结点j 之间相连接的路径上的信息素浓度为cij。初始时刻，蚂蚁放置在不同结点里，且各结点连接路径上的信息素浓度相同[13]，然后蚂蚁按一定的概率选择路线。不妨将Pk ij(t)设为t 时刻蚂蚁k 从结点i 转移到结点j 的概率。“蚂蚁TSP”策略收到两方面的左右，首先是访问某结点的概率，这个概率的大小依赖于其他蚂蚁释放的信息素浓度。所以定义：

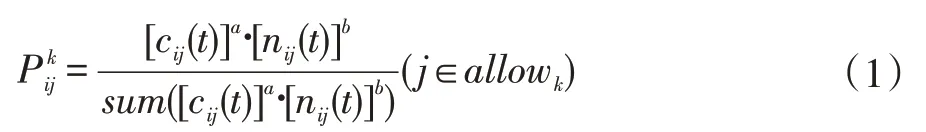
式中，nkij(t)为启发函数，表示蚂蚁从结点i 转移到结点j 的概率；allowk为蚂蚁k 下一步可转移结点的集合，随着时间的推移，allowk储存的元素数量会减小，最终会变为空集合。a 为信息素重要程度因子。

与实际情况类似的一点是：随着时间的推移，残留在路径上的信息素会逐渐挥发，蚂蚁在经过路径时残留的信息素量也会逐渐等同于信息素挥发量，最终使信息素残留量趋于稳定。令α表示信息素挥发程度，那么所有蚂蚁遍历完所有结点之后，各路径上的信息素残留量的数学表达式如下：

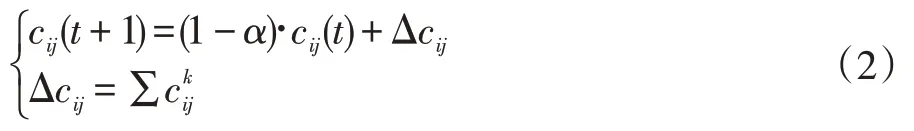
Δ为所有蚂蚁在结点i 与结点k 连接路径上释放信息素而增加的信息素浓度，通常情况下：

式中，Q 为路径信息素常量，l 为第k 只蚂蚁所经过路径的总长度。

2 蚁群算法的改进

2.1 初始信息素浓度的赋值

在传统蚁群算法中，各条路径上的初始信息素浓度相等，这意味着在第一次迭代时各个结点对蚂蚁有相同的吸引力，这样会造成以下两个弊端[13]：

（1）初始信息素的浓度不具有指导性，使得算法收敛速度过慢。

（2）前几次迭代蚂蚁有概率向错误的路径转移，信息素在错误的路径上残留，导致算法易陷入局部最优。

为了解决以上两个问题，本文对信息素浓度赋以合理的初值，确保算法向正确的方向收敛。初始信息素浓度的具体数学表达式如下：

其中，k0为常数，确保各条路径上初始信息素浓度在合理的范围内，dij为结点i 与结点j 的欧几里得距离（直线距离），τij为连接结点i 与结点j 的路径的初始信息素浓度。dij与τij呈反比关系，意味着初次迭代中距离越短的路径对蚂蚁有越强的吸引力，使各条路径上的初始信息素浓度在算法收敛的过程中有着合理的导向性，增大了最优路径被选择的概率。一定程度上加快了算法的收敛速度并避免陷入局部最优的情况。

2.2 信息素的更新策略

由于蚁群算法的正反馈机制，随着时间的推移，蚁群算法会逐渐收敛，各条路径上的信息素浓度更多的集中在当前最优路径上，使得每次蚂蚁所选择各条路径的概率趋于稳定，此时容易忽略潜在的最优路径，那么便有了陷入局部最优的可能。为了增强算法的全局搜索能力，减少局部最优发生的概率，需要提出一种更合理的信息更新策略。在迭代次数较小时，需要保证蚂蚁在路径上留下信息素浓度足够高，以确保迭代初期算法能更快的收敛，而当算法收敛到一定程度时，如果多次迭代中算法所求得最优路径长度一直未发生变化，那么算法既有可能已经得到了正确结果，也有可能陷入局部最优得到了有一定偏差的结果。此时为了避免算法陷入局部最优，需要适当增加信息素挥发量以及减小蚂蚁走过路径留下的信息素量，避免信息素过于集中，使得蚂蚁能有更大概率去探索潜在的最优路径，提高算法的全局搜索能力。为方便算法的描述，给出如下定义：

定义如果存在某个时间节点T0，在T0之前的固定时长范围内，算法所探索的最优路径未发生变化，则称该时间结点T0为信息素发散点。

每次迭代信息素更新的具体数学表达式如下：

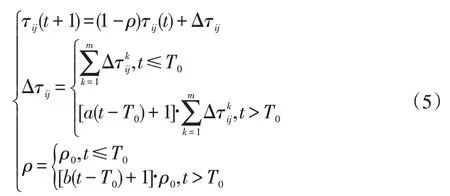
式中，τij为连接结点i 与结点j 的路径上的信息素浓度，Δτk ij为本次迭代中蚂蚁k 在路径上留下的信息素量，ρ为信息素挥发比率，a,b 为常数，控制当时间t 在过了信息素发散点后信息素的增加量和挥发量。

2.3 信息素矩阵的重置

尽管式（5）和文献[15]所给出的信息素更新方案能一定程度上避免陷入局部最优，但是并不能完全排除陷入局部最优的可能，为了更大程度上避免陷入局部最优的可能，我们在这里引入了熔断机制——当时间达到信息素发散点后的一段固定时间内，如果最优路径并没有发生变化，则将信息素矩阵按式（4）的方式重新进行赋值。

2.4 改进蚁群算法的具体流程

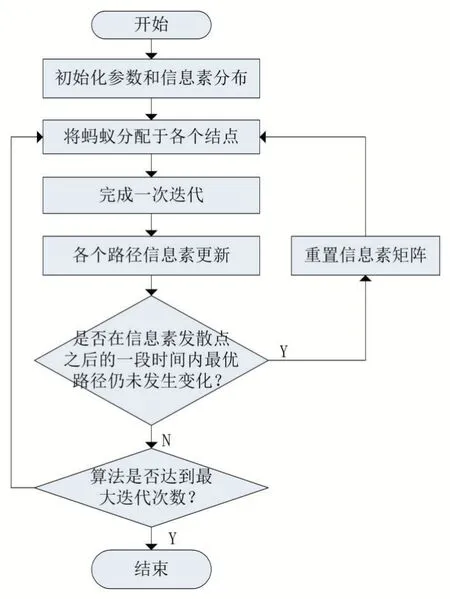
图1 改进后蚁群算法流程图

3 仿真实验

为对改进后蚁群算法的有效性与合理性进行验证，在五组结点位置坐标互不相同的平面图上通过MATALB 2018b 进行编程，用改进后的算法与传统蚁群算法进行比对。初始参数如下：α=1，β=5，ρ=0.1，Nmax=800，T=70，m=6，a=0.02，b=0.02，k0=100。

按以上参数分别代入改进后蚁群算法与传统蚁群算法，对每种情况分别求解1000 次求得结果如表1 所示。在得到表1 所示结果后对两种算法的正确收敛情况和平均路径长度减少情况进行比对后求得结果如表2 所示。

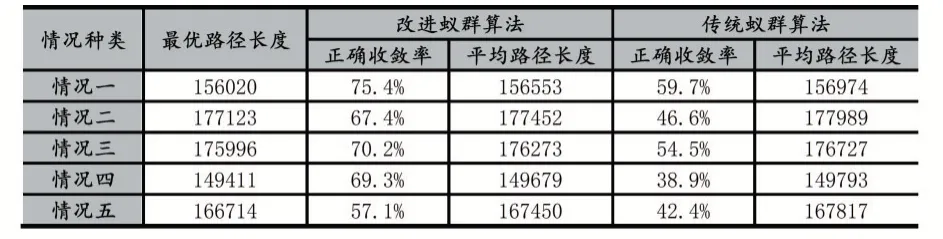
表1 两种算法正确收敛率与绝对误差值表

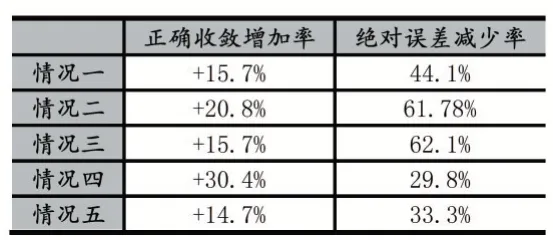
表2 算法正确收敛增加率与绝对误差值减少率表

对比五种不同情况下的改进后蚁群算法与传统蚁群算法的正确收敛率和绝对误差，我们可以发现在相同的参数设置下改进后的蚁群算法能更好地规避局部收敛的情况，增加算法正确收敛的比率，从而大大减小求解误差，得到更精确的答案。

4 结语

通过对蚁群算法的改进，使得蚁群算法在解决TSP 问题的过程中能更有效地规避算法陷入局部收敛的情况，提高算法的全局搜索能力，从而提高结果求解的精确度。然而，在本文对算法的改进中要求足够多的迭代次数以判别算法可能陷入局部收敛的情况，这是采用本文提出的改进方法的局限性。另外，本文对算法引入了新的参量，对这些参量赋以不同的值会对结果产生不同程度的影响，如何这些参数设置不当，会使得算法的全局搜索能力大大下降。因此，合理设置这些参数的值成为了本文算法应用的一个难点。但总体来说，本文提出的改进蚁群算法能很大程度上克服蚁群算法易陷入局部最优的弊端，在求解诸如TSP 问题之类的最短路径问题中有较好的适用性。