考虑员工加班和间接成本的多项目活动调度研究

施国洪　尹建建　张祖胜

摘要：文章在传统项目调度模型基础上，引入员工加班方案和间接成本，以项目完成时间和成本费用最小为目标，以项目活动顺序和员工最大加班时间为约束，建立多目标优化模型。通过设计充分利用员工可用加班时间的算法，得到各活动可选加班方案，求解多目标模型的帕累托解集。用无量纲化目标加权在所得的帕累托解集中选择满意解，以达到平衡项目工期和成本的目的。实例表明，该模型能有效确定工期短费用低的调度方案集合，为调度决策提供依据。

关键词：项目调度;员工加班;间接成本;多目标优化;遗传算法

一、前言

项目管理的意义在于合理利用资源，在保证项目的顺利实施的前提下，使企业的相关利益最大化。在新环境下，企业竞争越来越激励，竞争重心发生了转移——由企业资金成本的竞争转向企业人力资本的竞争。人力资源是项目管理中一类极为重要的资源，人员的调度就是让合适的人在合适的时间去从事合适的任务。人力资源的安排直接影响项目的工期和成本等绩效，目前已有较多研究。卢鹏宇等 基于项目演进时间片段使用启发式搜索进行人力资源调度。Jun等采用遗传算法对施工项目中的班次计划表进行了优化。Wu和Sun使用遗传算法解决了考虑员工学习效应的多项目人力资源调度问题。Campbell指出对员工进行交叉训练后制定的人力资源安排更好。Kazemipoor等采用差分进化的元启发式算法研究了多技能多项目的组合调度问题。付芳等运用列生成法对员工技能水平不同的多项目人力资源调度问题进行求解。Drezet和Billaut综合贪心算法和禁忌搜索方法，在符合相关法律前提下研究了人力资源约束下的项目调度问题。Chen等综合事件调度器和蚁群优化算法求解软件项目调度问题。

以上文献研究主要集中在员工多技能调度，多项目调度以及人员排班等问题上，对于采取员工加班的项目调度研究还较少。加班制度已经逐渐受到企业和国家的重视，出台的相关法律规定了劳动者的加班时间，调度决策中考虑员工加班意义重大。人力资源是一类特殊的可更新资源，存在一定的加班余量，对项目的成本和质量有很大影响。李明等采用遗传算法对员工加班调度进行研究。但其所设计的加班模型有所不足，不能很好挖掘员工的加班潜力。而且其成本模型未考虑间接成本，与现阶段现实脱离较大。随着产业服务的快速转型，诸如服务费、管理费等间接成本费用节节攀升，占总成本比重逐渐变大。以上多数文献的模型都存在忽视间接成本的不足。

在前人已有研究的基础上，根据现有法律法规对加班时间的约束，本文考虑项目员工加班和间接成本，建立以完成时间和成本费用最小为目标的优化模型，并采用并列选择遗传算法求解。其中，为充分挖掘员工加班潜力，设计一种最大利用员工可用加班时间的算法，从而计算出每个活动的加班模式集合。最后，结合实例的计算结果验证了模型和算法的有效性。

二、模型建立

项目网络图是由若干活动按一定的邏辑排列组成。考虑员工加班因素后，每个活动可以有多种工作（加班）模式，每种模式的活动完成时间和成本各不相同。据此，考虑员工加班和间接成本两大因素，建立以完成时间和成本费用最小为目标的多目标数学模型，也称工期——成本模型。

（一）模型建立的前提假设

为了使问题能被简化描述，在模型建立前进行假设。

假设一：相邻两个活动之间应为紧前紧后关系。即活动之间应满足“完成—开始”的顺序关系，不允许提前，也不考虑活动之间的时滞。

假设二：每项项目活动的人员固定，且存在整体约束。即活动进行所需人员一定，且数据已知，所有人员须同时进行标准活动和加班活动。

假设三：每个员工为满足相应活动要求的标准员工。即不考虑员工能力水平，效率的不同，每个员工的单位成本相同，且该数据已知。员工加班时间以小时/h为单位，且应满足国家法律的相关要求。我国法律规定：“职工每日工作8小时、每周工作40小时”。即平均每周休息两天，考虑国定节假期，休息日与工作日的比值约为0.4。

假设四：每个活动在员工正常工作状态下的活动持续时间已知，活动持续时间以天/d为单位，各种加班模式数据依照正常工作活动数据在相关约束下确定。

假设五：直接成本主要包括人工和材料两个方面。知道各活动在标准状态下的活动持续时间和员工每天的正常工作时间，项目的总时间是可以知道的。单位时间的材料费用一定，材料成本可看作一个常数，对调度结果不影响，可忽略;而由于加班和标准状态的员工小时工资不同，人工成本需根据模式具体计算。间接成本与项目工期有关，工期越长，间接成本越高。可由单位时间的间接成本费率计算间接成本，该数据可由专家估计或预算书分摊计算得到。

（二）数学模型

模型参数定义如下：

CT（completion time）表示项目完成总时间，包含工作日和节假日;RC（resource cost）表示项目成本总费用;i表示活动编号，0≤j≤N+1，N表示活动总数，0和N+1为虚活动，不增加时间和成本;ic表示单位时间间接成本费率;STj表示活动开始时间;FTj表示活动结束时间;t表示项目持续时间跨越的月度;Tj表示活动的作业总需时长;Pj表示活动的紧前活动的集合;rj表示活动所需人数，在虚活动中取值为0;Sj表示活动的加班模式，Sj∈{0，1，…，mj}，Sj=0表示加班时间为0，即正常工作模式;mj表示活动能采取的加班模式数量，包含正常工作模式在内，每个活动都有（mj+1）种加班模式可供选择，虚活动mj=0;wj表示活动的员工正常工作状态小时工资（元/h）;wj表示活动的员工加班工作状态小时工资（元/h）;Δt表示活动在加班模式Sj下的员工加班总时间，加班时间最小单位为1h，据相关法律规定，每人每天加班时间不能超过三个小时，即员工每天最多工作11h;D表示活动在加班模式Sj下的持续时间（不含节假日时间），单位为d;c表示活动在加班模式Sj下的人工成本，是正常工作人工成本和加班工作人工成本的总和。

据上述描述假设，以最小化项目完成时间和项目成本费用为目标，建立工期——成本多目标优化模型。

目标函数：min（z1=CT，z2=RC）（1）

其中 CT=[30×t+（max{FTN+1}-20×t）×（1+0.4）]（2）

RC=ic×CT+∑c（3）

约束条件：

STj≥max{FTi}?i，j∈Pj（4）

FTi=STj+D（5）

t=

（6）

Tj=rj×D×8（7）

≤3，?j，?Sj（8）

c=8×rj×wj×D+Δt×wj（9）

0≤Sj≤mj，?Sj∈{0，1，…，mj}（10）

模型中，式（1）为总优化目标，同时考虑项目完成时间和项目成本费用2个子目标;式（2）和式（3）为优化子目标，分别表示项目完成时间和项目成本费用。项目完成时间包含节假日，由于节假日与工作日存在比例关系，实际上是优化项目工作日时间。根据前提假设，项目成本费用实际只包含两部分，直接人工成本和间接成本，间接成本与项目完成时间有关。

模型约束中，式（4）为相邻活动之间的逻辑约束，活动开始时间必须比其所有紧前活动的最大结束时间大;式（5）为在所选加班模式下，相应活动完成时的时间;式（6）为项目持续时间跨越的月度;式（7）为相应活动的作业总需时长;式（8）为加班时间约束，员工每天加班时间不能超过法律规定的3个小时;式（9）为在所选加班模式下，完成相应活动需支付的人工成本，是正常工作人工成本和加班工作人工成本之和;式（10）为加班模式选择约束，必须在活动可行的加班模式中进行选择。

三、模型实施

本文模型有2个模块：初始化模块，初始化各活动的可行加班方案;多目标遗传算法模块，对项目可行加班方案的初始种群进行多次迭代选择，搜寻在多目标下的帕累托解集。

（一）初始化模块

初始化模块，其功能是对基本数据信息进行加工处理，确定项目中各活动可行的加班模式集合。模块需输入项目相关数据：活动j所需人数rj;活动j的员工正常工作小时工资wj;活动j的员工加班工作小时工资w;活动j在初始状态下的活动持续时间D;活动j的紧前活动的集合Pj。

各活动的加班模式应符合相关法律法规的约束。我国《劳动法》规定：“一天加班时间不能超过3个小时，一个月不能超过36个小时。安排劳动者延长工作时间的，支付不低于工资150%的工资报酬;休息日安排劳动者工作又不能安排补休的，支付不低于工资200%的工资报酬;法定休假日安排劳动者工作的，支付不低于工资300%的工资报酬。”根据法律法规，为方便计算，本模块对加班时间有如下假定：

1. 加班安排仅考虑延长劳动者工作时间的模式，不考虑节假日及休息日模式。假定加班工作小时工资w为正常工作小时工资wj的1.5倍。

2. 员工每日正常工作8小时，每天延长的工作时间不得超过3小时，加班最小单位为1小时，即加班模式下，员工每日工作时长在8～11小时之间。

3. 假定每月的标准工作日为20天，活动持续时间的最小单位为1天。每月加班时间不超过36小时。

4. 加班应满足整体约束，集体所有人员均参与加班，不考虑部分人进行加班工作的情况。

在上述约束条件下，以最大利用为原则，设计一种充分利用员工可用加班时间的算法流程，以此确定项目中各活动的加班模式集合。设计的这种算法能在法律约束下最大程度地利用员工可延长时间的加班方式，计算出每个活动的所有可行加班模式。

活动j的作业总需时长Tj Tj=rj×D×8（11）

活动j员工一个月最多工作时长MTj MTj=rj×36+rj×8×20（12）

活动j续tj个月 tj=

（13）

员工加班3小时的集体每天加班时间 ΔDTj ΔDTj=rj×11（14）

活动j最短持续时间min{D} min{D}=

+20×t （15）

活动j能采取的加班模式数量mj mj=D-min{D}（16）

可知活动j的加班模式Sj Sj∈{0，1，…，mj}

活动j在模式Sj的持续时间D D=D-Sj（17）

活动j在模式Sj的总加班时间Δt Δt=Tj-D×rj×8（18）

活动j在模式Sj的人工成本c c=rj×8×wj×D×Δt×wj（19）

（二）遗传算法模块

遗传算法模块，其功能是对初始化模块确定的各活动可行加班方案进行组合生成可行的项目加班方案，利用并列选择遗传算法對这些可行的项目加班方案进行多次选择和优化，搜寻在多目标下的帕累托解集。

组合优化问题的表述为：假定一个项目有m项活动，每项活动有n种加班模式，那么该项目的组合方案有mn种。这里使用遗传算法对此类问题进行多目标寻化。遗传算法是一种启发式搜索，不是盲目穷举，模拟自然界优胜劣汰的选择模式寻求全局最优，解决此类问题效果较好。

遗传算法采用并列选择法对多目标问题进行目标优化。其思路如下：首先，对种群的全部个体按子目标函数数目进行均等划分，一个子群体分配一个子目标函数，各子目标函数在其相应的子种群中进行独立地选择操作，各自选择一些适应度高的个体组成相应新的子种群;然后，将这些新子种群合并成完整群体，作为父代，在这个父代群体中进行交叉和变异操作，进而生成完整的子代群体;不断地重复“分割——并列选择——合并”操作，最终可得到多目标问题的帕累托解集。

1. 编码。采取基于活动列表的编码方式，染色体上的基因位数目为项目活动数（包括虚拟活动时），每个基因位为项目中相应活动所采取的加班模式。染色体编码和项目加班方案互相映射，确定了各活动的加班模式，一个项目加班方案也就确定了，具有良好的完备性。图1给出一条染色体编码，编码序列为（0，1，4，0，5，3，7，3，0），表示所对应项目有7项活动（序列前后为0的基因位表示虚拟活动），活动1加班模式为S1，活动2加班模式为S4，活动3加班模式为S0，依次类推。基于每个基因位对应的活动加班模式，可计算出项目的工期和成本，也就相应能确定染色体对应的适应度大小，为个体选择提供依据。

2. 选择。采用轮盘赌的选择方法筛选保留种群中的较优个体，继承优解和保持种群个体多样性，为下一步交叉操作贡献优质基因。适应度是评价各个体优劣程度的指标，适应度越大，被保留的概率也就越大。模型目标是成本工期越小越好，因此，划分的两个子种群对应的适应度函数分别为各子种群对应的目标函数，目标值越小，种群个体的适应度值越大，被选择保留的概率越大。将选择出来的两个新子种群合并为一个完整的种群作为父代，为交叉操作做准备。

3. 交叉。由于不同个体在相同基因位的可取值范围[0，mj]相同，这里采取简单单点交叉方式。从父代种群中选出满足交叉概率Pc的方案集合，对集合中相邻两个个体F1，F2进行交叉操作，随机确定交叉的位置j∈[1，N+1]，则生成的子代Z1和Z2在j前的基因分别和在j点前的基因相同，在后的基因分别和F1和F2在j点后的基因相同。交叉操作是遗传算法的关键，可将父代中的优良基因继承给子代，加快收敛速度。

4. 变异。采用基本位变异方式。其过程为先选出满足变异概率Pc的方案集合，对每个选中的个体随机确定其变异位置j∈[1，N+2]，对该点的基因值Sj重新定义，赋予其在取值范围[0，mj]内随机产生的一个新值，得到子代。变异操作是产生新个体的辅助方法，能有效保持种群个体的多样性，与交叉操作相配合能有效保证遗传算法的有效性。

四、实例验证

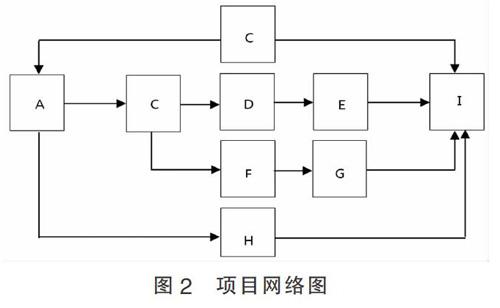
为体现本文所设计模型算法的优越性，对文献中的项目实例进行研究，项目网络计划如图2所示。项目各活动的正常工作活动时间、活动参与人员数量、员工正常工作小时工资保持不变，补充项目每天所需的管理费用（间接成本费率）数据，如表1所示。

为凸显间接成本对调度结果的影响，这里分别取间接成本ic=0，500，1000作比较。其中，活动A、I为虚拟活动，它们的各数据均记为0。

按照上述设计编制程序，基于MATLAB R2014a平台开发实现，在2.6GHz双核处理器、4GB内存的计算机上运行，进行多次结果搜索。

（一）初始化模块——生成活动可行加班模式集合

通过初始化模块，确定项目中各活动可行的加班模式集合。根据模块的功能设计，模块运行结果如表2所示。文献活动A-I的加班模式集合数量分别为[1，5，5，3，7，5，9，5，1]，而本模型得到的集合数量为，加班模式活动B增加1个，活动H增加2个，说明本文设计模型能更加充分挖掘企业员工的加班潜力。

（二）遗传算法寻优

对初始化模块确定的各活动可行加班方案进行组合生成可行的项目加班方案。基于活动列表的编码方式，将项目加班方案改编成机器可识别的染色体编码序列。根据各活动可行的加班模式数量，定出染色体基因座，基因座定义了染色体每个基因位上的取值范围。

遗传算法的相关参数设置如下：种群规模，将其划分为两个包含50个染色体的子种群，分别将项目工期和成本作为子种群的目标函数;交叉概率;变异概率;终止代。执行算法模块，确定出ic分别取0元/天、500元/天、1000元/天的帕累托解集如表3、表4、表5所示。观察三张表数据可以看出，间接成本对项目调度计划有很大影响，不可忽略。间接成本越大，帕累托解集逐渐向工期短的方案集中，可供選择的项目方案也越少。

（三）帕累托解集的决策

根据算法得到帕累托解集后，决策者面临在解集中选出适合企业情况满意方案的问题。企业在不同时期不同阶段的着重点不同，因此，满意方案很大程度上需要根据决策者的主观经验决定，如决策指标的重要度排序。

这里的两个指标分别为项目工期和成本。由于两个指标在数量级和单位上互不相同，影响对满意方案的确定，这里对这两个评价指标进行无量纲化处理。采取无量纲化方法中的“均值化”处理方法，它在多目标评价中效果较好，计算公式如下：

x=（20）

其中，μ为指标j的样本均值。

以表4为例，运用上述公式对ic=500的帕累托解集进行处理。通过决策者评价和专家打分综合评价确定各目标权重系数ωj。各方案的综合评价模型如下：

yi=∑ωjxij（21）

这里拟取CT权重系数ω1=0.3，RC权重系数ω2=0.7。将数据代入公式，计算出各方案的综合评价值为y=[0.974009;0.97957;0.983214;0.99242;0.996307;1.001787;1.005513;1.014961;1.024247;1.027973]向量y中最小值所对应的方案即为满意方案， min（y）=0.974009，即解集中的方案一为项目满意解。

五、结语

本文在现有法律对加班时间的约束下，考虑项目员工加班和间接成本，建立了以完成时间和成本费用最小为目标的项目调度模型，利用并列选择遗传算法求解问题，得到模型的帕累托解集。算法中设计一种最大程度利用员工可延长时间的算法，以此挖掘最大加班潜力，确定每个活动可选的加班模式集合。对比间接成本不同取值下的帕累托解集，揭示了间接成本对项目调度计划有很大影响。

对实例应用分析，验证了所提方法的实用性与有效性。结果显示，本文方法能快速识别各个活动的最大加班潜力，有效确定工期短成本低的调度方案集合，实现项目工期与成本费用的平衡。最后用综合无量纲化的目標加权法帮助决策者在解集中选出满意方案。

参考文献：

[1]李圆圆.新环境下企业人力资源管理调配问题及对策[J].湖北经济学院学报（人文社会科学版），2016，13（04）：61-62.

[2]任守纲，徐焕良，李相全.基于遗传算法的软件项目人力资源调度研究[J].计算机应用研究，2008， 25（12）：3563-3567.

[3]芦鹏宇，孙文俊，井瑞.基于时间片段的多IT项目人力资源调度问题求解[J].系统工程理论与实践，2012，32（04）：731-737.

[4]Jun D H， El-Rayes K. Optimizing the utilization of multiple labor shifts in construction projects[J].Automation in Construction，2010，19（02）：109-119.

[5]Wu M C， Sun S H. A project scheduling and staff assignment model considering learning effect[J].The International Journal of Advanced Manufacturing Technology，2006，28（11）：1190-1195.

[6]Campbell G M. Cross-Utilization of Workers Whose Capabilities Differ[J]. Management Science，1999，45（05）：722-732.

[7]Campbell G M， Diaby M. Development and evaluation of an assignment heuristic for allocating cross-trained workers[J].European Journal of Operational Research， 2002，138（01）：9-20.

[8]Campbell G M.A two-stage stochastic program for scheduling and allocating cross-trained workers[J]. Journal of the Operational Research Society，2011，62（06）：1038-1047.

[9]Kazemipoor H， Tavakkoli-Moghaddam R， Shahnazari-Shahrezaei P， et al. A differential evolution algorithm to solve multi-skilled project portfolio scheduling problems[J].The International Journal of Advanced Manufacturing Technology，2013， 64（05）：1099-1111.

[10]付芳，周泓.多项目人力资源调度实证研究[J].管理工程学报，2011，25（03）：73-77.

[11]Drezet L E， Billaut J C. A project scheduling problem with labour constraints and time-dependent activities requirements[J].International Journal of Production Economics，2008，112（01）：217-225.

[12]Chen W N， Zhang J. Ant Colony Optimization for Software Project Scheduling and Staffing with an Event-Based Scheduler[J].IEEE Transactions on Software Engineering，2013，39（01）：1-17.

[13]应瑛，寿涌毅.柔性工时约束下项目调度及其蚁群算法[J].计算机应用，2009，29（06）：1527-1528.

[14]Li H， Love P E D， Drew D S. Effects of overtime work and additional resources on project cost and quality[J].Engineering， Construction and Architectural Management，2000，07（03）：211-220.

[15]李明，徐哲，廖婷婷.项目员工加班调度多目标优化模型与算法[J].工业工程，2014，17（01）：37-43.

[16]姜健，赵杰，臧希喆.基于并列选择遗传算法的多机器人协作探测[J].计算机工程与设计，2008，29（05）：1218-1221.

[17]张卫华，赵铭军.指标无量纲化方法对综合评价结果可靠性的影响及其实证分析[J].统计与信息论坛，2005，20（03）：33-36.

（作者单位：施国洪、尹建建，江苏大学管理学院;张祖胜，重庆大学机械工程学院）