ACD模型自加权LAD估计的渐近性质

傅可昂, 吴梦雪, 黄 炜, 王江峰

(1. 浙大城市学院 计算机与计算科学学院, 浙江杭州310015;2. 浙江工商大学统计与数学学院, 浙江杭州310018;3. 浙江大学 数学科学学院, 浙江杭州310027)

§1 引 言

随着计算机技术的进步和发展, 数据存储和记录的成本越来越低, 人们可以获得金融市场上每笔交易的实时数据, 即获得采样频率越来越高的数据, 这些数据往往被称为高频数据. 通过对高频数据的分析, 人们能正确地揭示金融市场的微观结构, 这就使得对高频数据的研究成为当前的一个研究热点. 由于金融市场中每笔交易的交易时间都是随机的, 而高频数据记录的正是实时交易产生的数据, 因此高频数据的一个显著特点就是交易之间的时间间隔(又称持续期)不规则. 这些不规则的时间间隔包含了许多市场微观信息(比如交易的聚集或分散), 必须出现在描述数据的模型中, 而采用传统的等间距计量模型对其建模则会丢失很多信息. 有鉴于此,Engle和Russel[1]提出了描述交易时间间隔的自回归条件持续期(ACD)模型, 从而开启了ACD模型及其应用的研究.

在连续的交易过程中, 记Tt为第t次交易发生的时间,xt=Tt −Tt−1表示第t −1次和第t次交易之间的时间间隔(持续期). ACD模型的主要思想是在自回归条件异方差模型的基础上, 采用一个标记的点过程来刻画交易时间到达的随机性. 标准的ACD(p,q)模型可表示为

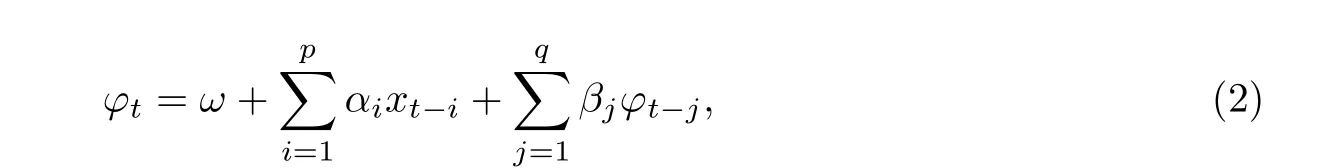
其中εt为独立同分布的非负误差项且满足Eεt= 1,ϕt= E(xt|Ft−1)为持续期xt的条件期望,Ft−1=σ(xt−1,··· ,x1)是前t −1次交易的信息集,p,q为模型的滞后阶数. 令θ:=(ω,α1,··· ,αp,β1,··· ,βq)T为模型参数. 由于持续期xt恒为正, 故ϕt也应该恒为正, 因此本文记参数空间Θ为Rp+q+10 中的紧集, 其中R0= (0,∞), θ0为参数θ的真实值. 众所周知, 高频数据还存在着明显的日内效应, 即在日内表现出周期性的规律, 因此结合Engle和Russel[1]的建议,本文的xt为去除日内效应后的持续期.

Engle和Russel[1]采用形如(1)和(2)式的模型, 在误差项服从指数分布和Weibull分布的条件下(此时的模型分别记为EACD和WACD模型), 较好地捕捉到了交易间隔的变化规律. 之后又有许多学者对ACD模型进行了多方面的推广, 有的提出了诸如误差项服从Gamma分布, Burr分布,Birnbaum-Saunders分布和Fr´echet分布的GACD,BACD,BS-ACD和FACD模型(见[2-5]),有的则在模型形式上进行了推广, 如Bauwens等[6]提出了Log-ACD模型, Zhang等[7]提出了门限ACD模型, 戴丽娜[8-9]采用非参数可加ACD模型和半参数ACD模型进行统计建模, Saart等[10]则对半参数ACD模型进行了理论分析探索.

在对目前运用较为广泛的参数ACD模型进行参数估计时, 应用最多的是拟极大似然估计(QMLE)方法. 众所周知, QMLE只有在假设模型误差方差有限的条件下, 才具有相合性和渐近正态性, 并且在估计过程中往往需要事先假设误差服从某种特定的分布. Lu和Ke[11]提出了广义最小二乘估计(GLSE), 并说明该估计比常用的QMLE较优, 但是它却要求数据的四阶矩有限.金融高频数据一般都呈现明显的“尖峰重尾”性, 其方差甚至可能无穷. 因此, 在ACD模型中要求误差方差有限显得不够合理, 并且一旦事先假定的误差分布与实际不符, 将会得出错误的结论.刘伟[12]对ACD模型采用了最小一乘(LAD)估计, 其主要优点是不用事先假定误差分布, 且不要求误差方差有限. 但是LAD估计也存在着一定的缺陷, 即面对具有极端值的数据时, LAD估计给所有数值以相同的权重, 这显然是不合理的.

为了弥补已有估计的不足, 本文拟对ACD模型采用自加权最小一乘(SLAD)估计(即根据数值自身特点给予不同的权重以降低极端值的影响), 并研究该估计的极限性质及其应用. 本文剩余部分结构如下:§2介绍一些基本概念后给出本文的主要结论(强相合性和渐近正态性),§3和§4分别给出了SLAD估计的数值模拟和实证分析结果,§5给出结论的证明过程.

§2 主要结论

由(2)式可知ϕt与θ有关, 故记ϕt为ϕt(θ). 对(1)式两端同时取对数, 可得

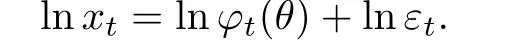
令yt=lnxt −c0,ηt=lnεt −c0, 其中c0=median(lnεt), 则有

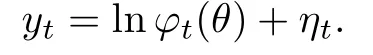
因此, 参数的SLAD估计为

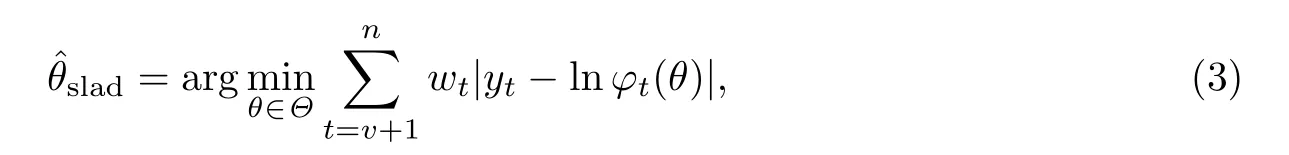
其中v=max(p,q),wt=wt(xt−1,xt−2,···)>0为一有界可测函数.

§3 数值模拟

本节将对参数的SLAD估计进行有限样本的模拟研究, 主要比较SLAD估计与QMLE和LAD估计在误差含有一定极端值时的表现以及SLAD估计的正态性表现. 考虑ACD(1,1)模型, 其中θ的真实值取(0.1,0.2,0.7), 误差项εt分别服从Exp(1), Lognormal(-0.5,1), Weibull(2,1.128),Pareto(2,1), Burr(3,0.5), Fr´echet(2,0.56)这六种期望为1的分布. 金融市场容易受新消息的影响,这种影响将直接导致持续期中存在较多的离群点(极端值), 这些离群点将直接影响估计效果.为了更好地体现金融数据的特点, 从产生的随机数中随机抽取5%的数据, 将这些数据加上分布的3倍样本标准差作为离群点. 在SLAD估计中, 选取

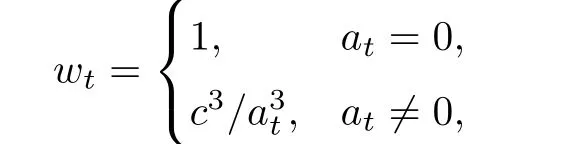
其中at=|xt−1|I(|xt−1|≥c),c为序列xt的95%分位数点.

产生样本容量为500的观察数据, 将重复运行2000次后的三种估计的平均偏差(Bias)和均方误差(MSE)进行比较, 具体结果如下表所示.

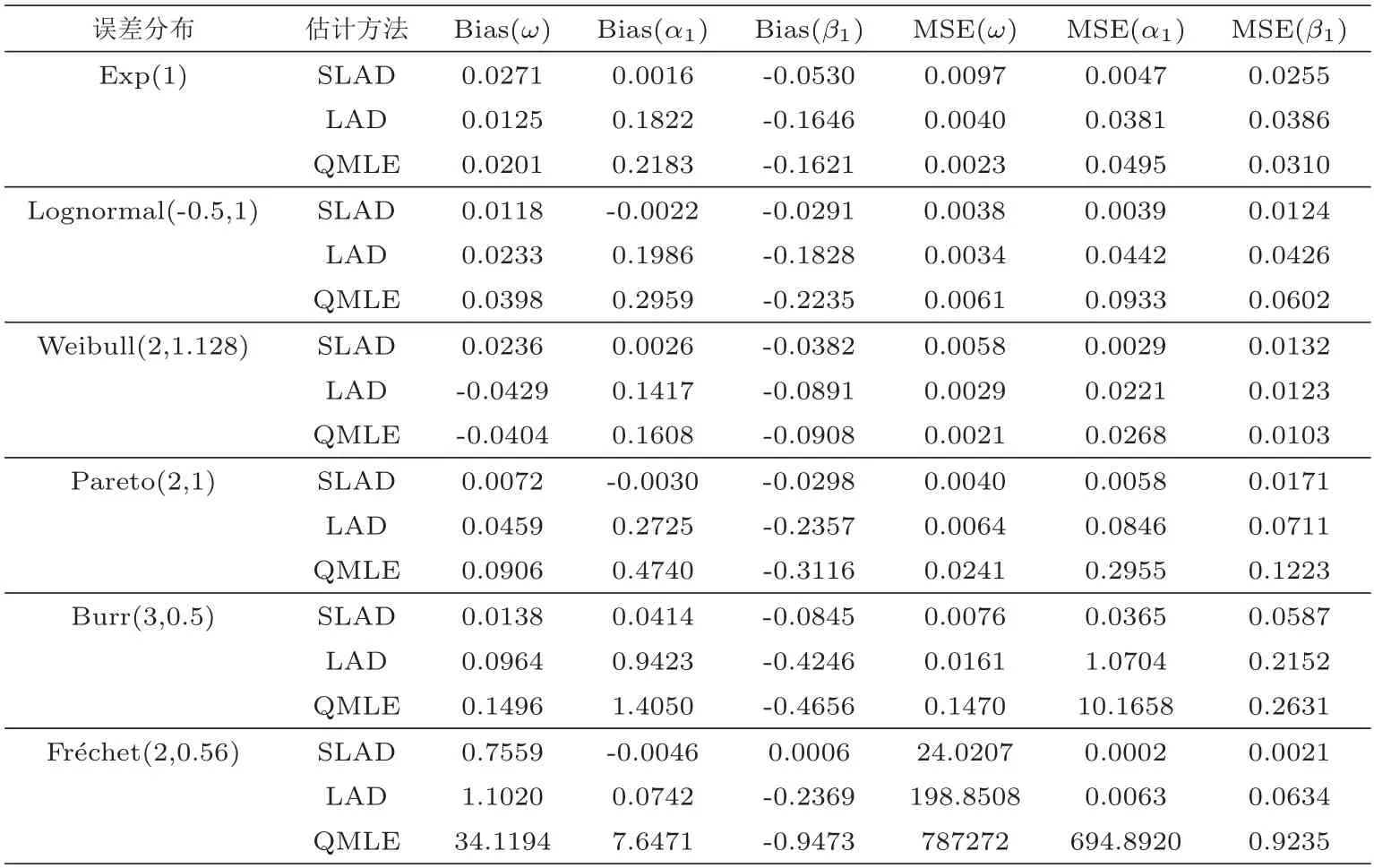
表1 不同分布下的估计结果比较

从表1可以看出, 不管是重尾还是轻尾误差分布, SLAD估计结果可以说整体上均好于LAD和QMLE. 这说明SLAD估计的结果更为稳健, 更适合具有重尾性和极端值的金融数据建模(对ACD(1,2), ACD(2,1), ACD(2,2)等高阶模型, 也可得到类似的模拟结果说明SLAD估计的结果较为稳健, 本节限于篇幅而未放高阶模型的数值模拟结果).

在误差分布服从Fr´echet(2,0.56)的条件下, 对按SLAD方法所得到的三个参数(ω,α1,β1)的估计值进行正态性检验, 所得QQ图如图1所示. 由图可知, SLAD方法所得估计符合§2中的渐近正态性结论.

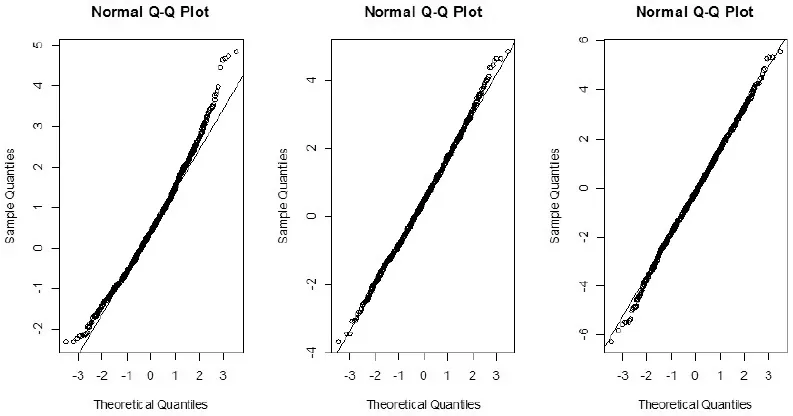
图1 ω(左), α1(中)和β1(右)的SLAD估计的QQ图

§4 实证分析

选取青岛海尔(600690)和宝信软件(600845)两只股票2017年6月19日至2017年6月23日的数据作为实证分析的样本. 价格持续期是指价格的变化超过一个给定的阈值所需的时间, 其中价格的变化指的是变化的绝对值. 在本节中, 将阈值设为0.01元, 即价格的绝对值每变化0.01元所需的时间即为一个价格持续期. 价格持续期可以用来衡量市场价格变化的速度和市场的流动性,投资者也可以根据对价格持续期的预测来及时地调整投资策略. 价格持续期越小, 说明市场波动性越大, 反之则越小. 图2和3分别给出了两只股票的部分原始价格持续期(纵坐标代表原始价格持续期值, 横坐标代表持续期序列值)散点图. 从图2和3这两张原始持续期图可以看出, 原始价格持续期存在着明显的聚集效应和日内效应(即在一天中持续期呈现出先增后减的趋势). 由于日内效应会影响模型的结果, 故同Engle和Russel[1]一样, 在建模前采用三次样条插值法去除价格持续期的日内效应. 样条节点分别为每个交易日的10: 00, 10: 30, 11: 00, 13: 30, 14: 00, 14:30. 去除日内效应前后, 价格持续期的描述性统计分析结果见表2和3.

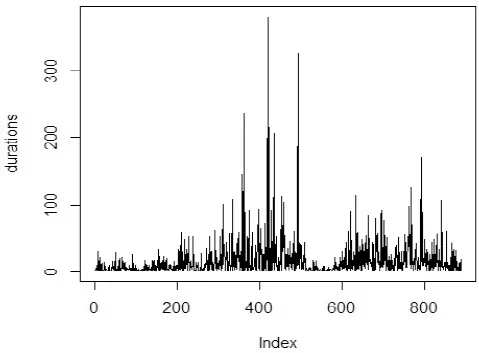
图3 宝信软件原始价格持续期

表2 原始价格持续期统计分析

表3 去除日内效应后价格持续期统计分析

对比表2和3可以发现, 去除日内效应后两只股票的价格持续期均值均接近于1且偏度和峰度都有所下降; 表中的偏度和峰度说明即使去除了日内效应, 两只股票的价格持续期也都不符合正态分布; 从Ljung-Box Q 统计量来看, 调整前后持续期的Q统计量值远大于阈值, 这表明原始价格持续期和去除日内效应后的价格持续期均存在着很强的自相关性, 同时也说明日内效应并不是导致价格持续期存在自相关性的唯一原因.

对去除日内效应后的价格持续期用QMLE建立WACD(1,1)模型(与GACD等模型相比,WACD模型估计结果相对较好), 同时应用SLAD和LAD方法估计ACD(1,1)模型参数. 具体结果如下表所示.

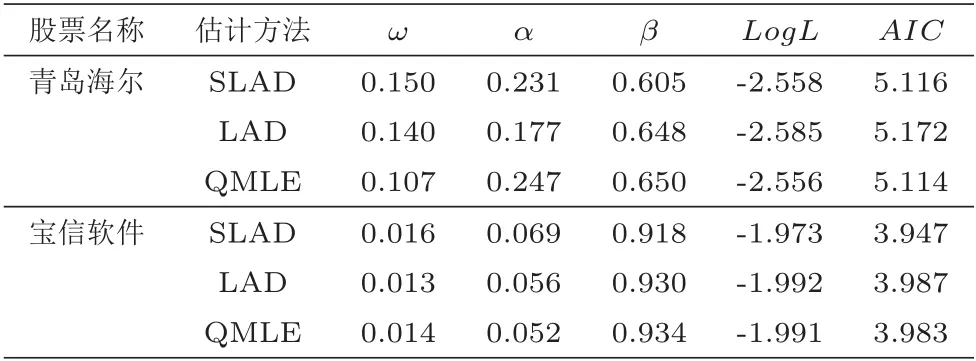
表4 三种估计结果对比表

从表4可以发现, 两只股票的α+β均小于1, 满足模型平稳性的要求, 且β的值远大于α, 说明价格持续期的期望受上一期期望的影响要大于上一期价格持续期;α+β的值均大于0.85, 说明其存在这较强的聚集效应. 从AIC等指标来看, SLAD估计的结果不比LAD和QMLE的结果差. 对应用SLAD方法建模估计后的残差(xt)进行自相关检验, 两只股票滞后10阶和20 阶的Ljung-BoxϕˆtQ 统计量分别为11.889(0.293), 23.587(0.261)和14.201(0.164), 23.124(0.283), 均接受了原假设,说明残差符合独立同分布的条件, 模型拟合得比较充分.

对残差序列采用Resnick[15]所介绍的Hill估计的方法估计尾部指数, 图4和5分别给出了青岛海尔和宝信软件价格持续期SLAD估计建模后残差序列的尾指数估计图. 从图中无法说明残差序列具有有限方差, 这也就意味着SLAD估计的结果相较而言更为可信.

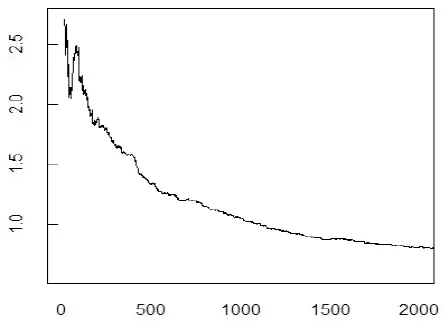
图4 青岛海尔尾指数估计图

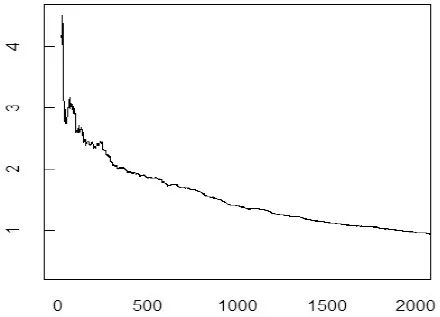
图5 宝信软件尾指数估计图

§5 结论证明