利用4n阶和幻方构造8n阶和幻方

张 婧，刘兴祥，刘娟娟

(延安大学数学与计算机科学学院，陕西延安716000)

矩阵是许多学科的基础工具，而幻方这类特殊的矩阵近年来研究的人层出不穷[1-10]。幻方首次是在十三世纪南宋数学家杨辉开始系统研究，欧洲十四世纪也开始了这方面的研究，著名数学家费尔玛、欧拉都进行过幻方研究。如今，幻方仍然是组合数学的研究课题之一，经过一代代数学家与数学爱好者的共同努力，幻方与它的变体所蕴含的各种神奇的科学性质正逐步得到揭示，它已在组合分析、实验设计、图论、数论、群、对策论、纺织、工艺美术、程序设计、人工智能等领域得到广泛应用。而本文在研究幻方的过程中，根据和幻方的定义和性质，得到和幻方的一种新的构造方法，利用已知一个低阶和幻方构造一个高阶和幻方。

1 预备知识

定义1[1]设矩阵A=(aij)m×n∈Zm×n，m,n∈N*，若矩阵A满足以下条件：

①m=n;

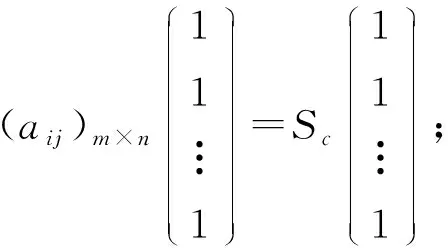
③(11…1)1×m(aij)m×n=Sl(11…1)1×n；

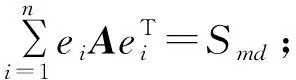
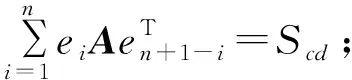
⑥Sc=Sl=Smd=Scd。

则称矩阵A=(aij)m×n为Z上的n阶和幻方，幻和记为S。

定义2[1]设矩阵A=(aij)n×n∈{1,2,…,n2}，n∈N*，若矩阵A满足以下条件：

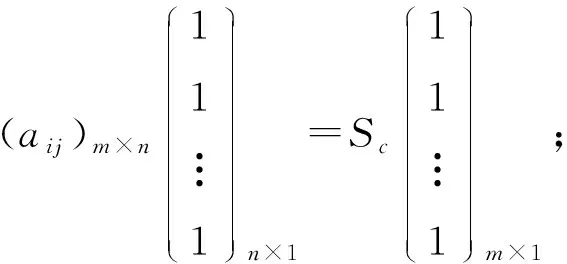
②(11…1)1×m(aij)m×n=Sl(11…1)1×n；

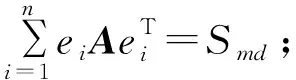
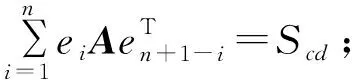
⑤Sc=Sl=Smd=Scd。

则称矩阵A=(aij)m×n为Z上的n阶始元和幻方，幻和记为S。

2 主要结果

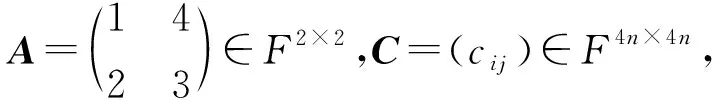
其中，Bij=

则矩阵D∈F8n×8n为8n阶和幻方，且幻和为256n3+4n。

证明因为C是4n阶始元和幻方，幻和为

32n3+2n=

4n(0+1+…+(4n-1))+(1+2+…+4n)=

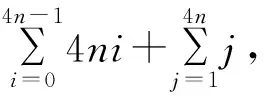
根据D的构造规律，记

则矩阵的的幻和为：

则矩阵D∈F8n×8n为8n阶和幻方，且幻和为256n3+4n。

例当n=1时，随机选取一个四阶和幻方C，

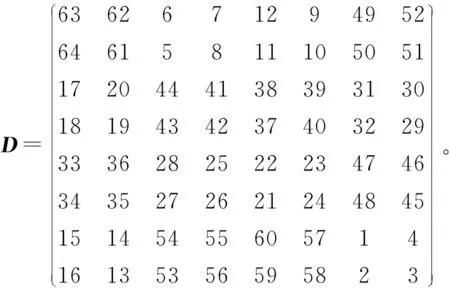
D就是一个8阶和幻方，幻和为260。