“乘”的想法始于哪儿

□郜舒竹

小学数学课程内容中，“乘”作为一种运算，其初步认识通常安排在二年级，学生已经学习了“加”的运算后。把“乘”视为“相同加数求和”，也就是“重复加（Repeated Addition）”的过程，目的是使加的过程简化。比如对于“2+2+2”，写为乘的算式就是“2×3”或“3×2”。在小学数学课程与教学中，普遍认识为：

●乘的初步认识是以加为基础的；

●乘的本质是加；

●乘是加的简便运算。

事实上，“乘”与“加”这两种运算存在很大差异。“乘”的想法并非源于“加”，更不仅仅是加的简便运算。“乘”的想法在“数数（音：shǔshù）”的过程中就已经出现了，而且这样的想法是先于“加”的。

一、“重复加”的窘境

美国哈佛大学数学教授吉斯·德芙林（Keith Devlin）于2008年在社交网站发文，强烈反对小学数学课程与教学中将“乘”定义为重复加，呼吁“停止重复加的说法”[1]。德芙林作为数学研究者，当然深知“乘”在数学中的意义。数学课程内容中，这样的意义是一个不断进化和演变的过程。

即便是低龄儿童，对于乘法的初步认识，“乘”与“加”的想法也是存在很大差异的。这里所说的“想法（Idea）”不同于通常所说的“算法”和“算理”，算法强调的是“操作（Manipulation）”和“程序（Pro⁃cedure）”，学习方式是“模仿+练习”，追求熟练，进而达到“又对又快”。“算理”是算法正确可行的理由或依据，这样的理由或依据追求的是逻辑上的正确，而不是学生认知过程中的意义生成。想法强调“意义生成（Sense Making）”，追求的是“理解（Un⁃derstanding）”。

“乘”作为运算，其意义在小学数学课程内容中，呈现出不断“进化（Evolution）”的动态特征。如果在小学中、低年级对乘运算形成的认识是“重复加”，那么到高年级学习诸如“0.2×0.3”或“小数和分数的运算，就会出现认知困难，这时的“乘”，已经失去了“加”的意义。

数学课程与教学的一个基本原理是“系统性（Coherence）”，类似于数学理论发展的“继承性（Permanence）”[2]。在课程或理论体系中，同一内容的意义可以在原有基础上“拓展（Extend）”，但不应“自相矛盾（Self Contradiction）”。对“乘”的认识，起初为“是加法”，而后又成为“非加法”，这样的是非混淆自然违背了课程与教学的系统性原理。

因此需要研究并挖掘“乘”这一运算相对稳定和一致的意义究竟是什么，这样的意义应当能够贯穿数学课程与内容的始终。在此基础上，就可以知道“乘”的认知起点究竟在哪儿。为此，先来探讨“乘”与“加”，在想法上的差异。

二、“增加”的两种眼光

人在日常活动中会无意识地使用加或乘的运算，自然数范围内二者都有“增加”的意义，比如：

●一瓶矿泉水2元，买3瓶，自然而然地使用乘法运算“二三得六”，使2元增加为6元，即“2元×3=6元”。

●如果今天是星期四，无须思索就会使用加法运算，想到再过两天即后天就是星期六，在星期四基础上增加2天，成为星期六，即“4＋2＝6”。

也有一些情境，如果看待“增加”的眼光不同，就会使用不同的运算，进而得到不同的结论。比如：假定有A、B两种植物，A植物2米高，B植物4米高。若干年后，二者都增高4米，A植物高度变为6米，B植物高度变为8米。

图1 植物生长示意图

如果把“生长”看作一个过程，这个过程应当包括三个要素：原有高度、增加高度和当前高度。三者的关系是“原有高度+增加高度=当前高度”。

从“增加高度”看，两种植物是相同的，都是在原有基础上增加了4米，从而使得A植物高度变为6米，B植物高度变为8米。用算式表达为：

A植物：2米+4米=6米

B植物：4米+4米=8米

如果此时关注两种植物生长的快慢，也就是对“生长速度”进行比较，用不同的眼光，就会出现不同的答案。

用“加”的眼光看，增长后当前高度是“原有”和“增加”高度的和。对于增长速度，如果只考虑“增加”的“米”数，不考虑原有高度，那么在相同时间内，两种植物“增加”的“米”数相同，可以说两种植物，在这段时间内增长的快慢是一样的，也就是增长速度是相同的。

另外一种是用“乘”的眼光，对于增长速度是看“相对于原有高度，增加的幅度”，将增加高度和当前高度的参照标准定位于原有高度，也就是将“单位一”视为“原有高度”，这个“单位一”对于A植物来说是2米，对于B植物来说是4米，二者是不同的。

A植物原有高度是2米，增长了4米，相当于原有高度又重复出现了“2次”，使得增长后的总高度6米包含了“3次”原有高度，或者说增长后的总高度包含了“3个”原有高度。这里出现的“次”和“个”，指向的单位不再是“1米”，而是“原有高度”。

所谓“乘”的眼光，首先是如何看待“1”，也就是“单位”。前面所说的“3次”或“3个”，可以统称为“3倍”。A植物增加了原有高度的2倍，增长后的高度是原有高度的3倍。B植物同样增长了4米，用原有高度4米作为单位一衡量，增长后高度8米是原有高度4米的2倍，都是将“原有高度”视为“单位”，两种植物的“单位”是不相同的。

在相同时间内，A植物高度增长为原来的3倍，即“原有高度×3”，也可以写为“3原有高度”。B植物高度增长为原来的2倍，即“原有高度×2”，写为“2原有高度”。因此用乘的眼光看，可以认为A植物相对于原有高度，比B植物相对于原有高度，增加的幅度更大，因此A植物比B植物增长速度快。

两种眼光，得到生长速度“既相同又不同”的判断。从形式逻辑的视角看，如果“相同”为真，那么“不同”为假；如果“不同”为真，那么“相同”为假。“相同”与“不同”作为相互对立的两个判断，不可能同真，也即不可能同时正确。为什么会出现这样违背逻辑的悖论？

原因就在于推理的大前提不同，由于看待“单位”的眼光不同，比较的对象发生了变化。如果说两种植物增长的高度相同，都是4米，前提是将“1米”视为单位，比较的对象是“增加的米数”，两种植物增加的米数都是4米，自然相同。

如果把“原有高度”视为“单位”，比较的对象是“相对于原有高度增加的幅度”，两种植物就不同了。A植物原有高度是2米，增长高度为4米，这时增加的幅度就成为“2个原有高度”，即“2个2米”。B植物原有高度是4米，增长高度也是4米，增加幅度就成为“1个原有高度”，也就是“1个4米”。正是因为看待单位的眼光变了，也就使得比较对象改变了，因而就出现了相悖的两个结论。因此可以说，“乘”的想法始于看待“单位”的眼光的改变。

三、“乘”与单位转换

综上可以归纳出“加”与“乘”意义上的差异。“加”是保持单位不变的运算，而“乘”是使得单位改变的运算。以A植物为例，用“加”的眼光看，其生长过程为：

●原有高度（2米）+增加高度（4米）=当前高度（6米）

算式中两个加数以及运算结果对应的单位都是“米”。原有高度和增加高度两个加数可以分别看待，是一种互不影响的并列关系，也可以看作是相互分离的两个局部构成一个整体的关系，通常用连接词“和”表达二者的关系。

如果用“乘”的眼光看，A植物生长过程可以用算式表示为：

●原有高度（2米）×3=当前高度（6米）

这个算式中的因数“3”的单位不是“米”，而且是不能独立存在的，与另外一个因数“原有高度”不是并列的关系，而是用“个”表达的包含关系，或用“的”表达的修饰或从属关系。比如“3个2米”，其中的“3个”是修饰“2米”的，也可以说“2米的3倍”，其中的“2米”从属于“3倍”。

因此乘法算式中参与运算的两个因数，是相互依赖与制约的关系。如果把“乘”运算看作“操作（Operation）”，那么两个因数各自的角色就分别是“被操作者”和“操作者”，也叫作“被动者（Oper⁃ant）”和“动者（Operator）”。历史上，为了区分乘法运算中的两个因数角色的不同，分别称它们为“被乘数（Multiplicand）”和“乘数（Multiplier）”。

“原有高度（2米）×3=当前高度（6米）”中的因数“3”，对应的“1”是前面的因数“2米”，脱离开前面的因数，这个“3”就没有意义，相当于“用3作用于2米”，因此“2米”是被乘数，“3”是作用于2米的乘数。乘的运算，就是将原有高度2米这个单位，改变成为6米。这里的6米，既可以看作“6个1米”，也可以看作“1个6米”，但无论如何已经失去了“3个2米”的意义。因此，乘在我国历史上被认为是“以数生数”的运算[3]，可以理解为将“2个3米”改变为“6个1米”或“1个6米”。

欧洲算术历史中，像“2米”这样表达具体量的数，也叫作“具体数（Concrete Number）”，如果把“2米”视为“单位一”，那么“3个2米”中的“3”就叫作“抽象数（Abstract Number）”。把具体数对应的单位叫作“原始单位（Primary Unit）”，抽象数对应的单位叫作“衍生单位（Derived Unit）”[4]。按照这样的说法，“乘”运算，其实就是将衍生单位改变为原始单位的过程。

用这样单位转换的眼光看，任何一个具体数，也就是以原始单位为单位的数，都可以用多种眼光看待。比如12个苹果，如果以“苹果”为单位是12，表示其中蕴含着12次“1个苹果”；如果以“12个苹果”为衍生单位，就是1，表示含有1次“12个苹果”。如果以“2个苹果”为衍生单位，12个苹果就是6，表示含有6次“2个苹果”。这样的关系都可以用乘法算式表达：

●1苹果×12=12苹果

●12苹果×1=12苹果

●2苹果×6=12苹果

单位转换的想法，在认知科学中叫作“意象图式转换（Image Schema Transformation）”，具体说就是“一”与“多”的相互转换，可以简称为“一多转换（Multiplex-Mass）”[5]。人类活动中，这样的思维方式十分普遍。比如12个苹果放满纸箱，这时眼中的“12个苹果”就转换为“1箱苹果”。再比如，远看很多头牛，视觉中的“多”在头脑中自然会成为“一”，也就是头脑中出现“一群牛”的意象。

图2 “一群牛”示意图

这样“一多转换”的思维方式其实是人的一种“认知能力（Cognitive Capacity）”，叫作“单位化（Unitizing）”。这种能力在数学认知过程中广泛应用。比如时间单位中的“2时等于120分”，同样的时间段，用“分”做单位，对应的数是120。用“时”做单位，就转变为“2”，其原因就在于将“60分”看作“单位”，命名为“1时”。“时”是从“分”这个原始单位衍生而来的衍生单位。同样道理，长度单位中将“100厘米”视为“单位”，命名为“1米”，“米”就成为相对于原始单位“厘米”的衍生单位。“乘”作为运算的一个重要意义，就是实现这样的单位转换。

四、“乘”的想法先于“加”

如果把“单位化”以及“单位转换”视为“乘”最初的想法，这样的想法并非始于加法运算，在“数数（Count）”和“记数（Numerals）”过程中已经出现。低龄儿童最初接触的运算就是“数数（Count）”。以数苹果为例：

图3 数苹果示意图

如果从左向右看，数数的过程实际是给每个苹果依次命名的过程：第一、第二、第三……每一个名称对应1个苹果。到最后数到“第六”，对应的是最右侧的1个苹果。

这时如果需要知道共有多少个苹果，思维中就需要把“第六个苹果”的“序数（Ordinal Number）”表达，转变为“共有6个苹果”的“基数（Cardinal Num⁃ber）”表达。这样的转变，不仅是语言的转变，实质是思维的转变。数到最后的“第六”，指向的对象是“1个苹果”，相应的“单位一”自然也是“1个苹果”。如果要想知道“共有多少个苹果”，就需要另外一个表达时间先后的概念，即一共数了6“次（Time）”，也就是“1个苹果的6倍”。用乘法算式表达，就是“1苹果×6=6苹果”。

算式中的因数“6”指向的单位不是“苹果”，而是数数动作出现的“次数”，是抽象的数。因此从“第六个苹果”转变为“共有6个苹果”，实质是“1个苹果”出现“6次”，也就是将“6次1个苹果”，转变为“1次6个苹果”的过程。这样的过程其实已经出现了“乘”的想法。

下面再来看数数过程中加的想法是如何出现的。图3中，如果数到“第二”时因故中断，然后需要重新开始，这时原来的“第三”自然成为重新开始的“第一”，依次类推。

图4 加法示意图

此时数数过程自然地分为两个阶段，第一阶段从序数转变为基数的结果是“共有2个苹果”，第二阶段同样的转变结果是“共有4个苹果”。

如果希望知道两个阶段的总数，又不希望重新数，就需要将两个阶段的结果“合并（Merge）”，这个合并的过程就产生了“加”的运算，写为算式就是“2苹果+4苹果=6苹果”。

如果把6个苹果看作一个整体，也就是一个集合，这时思维的提升在于出现了整体中的部分，也就是“子集”的概念。数数的两个阶段分别得到两个结果“2苹果”和“4苹果”，成为两个局部，两个局部合并成为整体“6苹果”。如果把这种合并的想法视为加的想法，自然是以序数转变为基数想法为基础的，因此说“乘”的想法并非始于“加”，而是先于“加”的。

更进一步，如果运用“一多转换”单位化的思维，数数过程中将“2个苹果”视为“1”，这时“6次”就变为“3次”，也就是3倍。

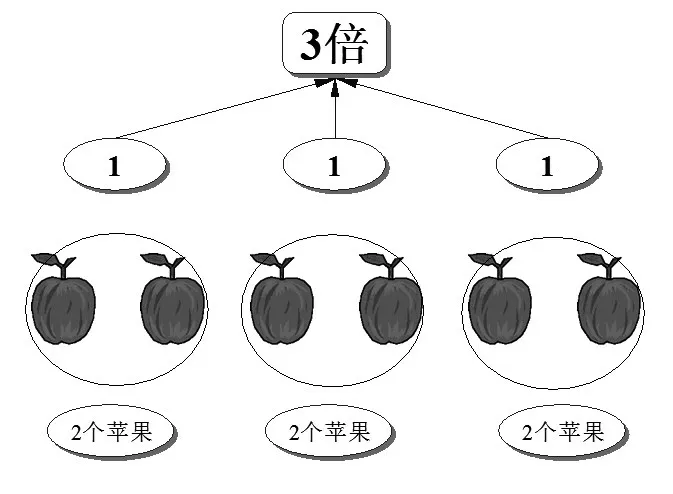
图5 乘法示意图

其中的“3次”或“3倍”，是原本苹果数量中所没有出现的数，是人将“2个苹果”视为“单位一”后出现的。写为乘法算式“2苹果×3”，其中的“3”就是表达“2苹果”出现3次，也就是“2苹果”这个衍生单位的3倍。

“2苹果×3”的出现，从想法看，并不是为了“2苹果+2苹果+2苹果”计算的简便，而是看待苹果的眼光发生变化，这样的变化体现为两方面，第一是看待“单位一”的眼光，第二是“单位一”之间的转化。

加的眼光是自始至终将“单位一”视为“1苹果”，两个加数和最后结果都是以“1苹果”为单位。因此加的想法相对单纯，并不出现看待“单位”的眼光变化，运算过程也不出现“单位”的转变。而“乘”的想法，既有看待单位眼光的变化，运算中也会出现单位的转化。

五、“单位化”的主观性与多样性

综上，乘的想法源于“单位化”的眼光。所谓“单位化”，指的是把什么看作“1”的问题。这样的眼光往往因人而异，具有主观性和多样性。古希腊时期欧几里得所著《原本》（Elements）中，并不认为“1”是数，而是一个“单位”，是度量数的标准，把“数”定义为“比（Ratio）”[6]，也即数的存在是相对于“单位”而言的。比如，“5”这个数是“5个1”的意思，离开了“1”，“5”是没有意义的。所以“5”实质是“5和1的比”。

这样的想法，在“记数”中也有体现。所谓记数，指的是用符号或语言表达数。比如目前仍然经常使用的罗马记数，“1，2，3”分别表示为“I，II，III”，其中的“II”和“III”都是以“I”为单位。符号“V”表示“5”，实际就是将“5个I”的“IIIII”，看作一个单位，用“V”表示“1个5”，也就是把“1的5倍”变成了“5的1倍”。

如今广泛使用的印度阿拉伯的十进制记数，如果把“1”看作单位，那么“10”表示“10个1”；如果把“10”看作单位，那么“30”就表示“3个10”。这也是为什么通常把“十，百，千，万，亿，兆”叫作记数单位。所以“30”原本是“30个1”。把“10”看作“单位”后，“30”就成为“3个10”，用乘法算式表示为1×30=10×3。等号左侧表示“1的30倍”，右侧表示“10的3倍”，看待“单位”的眼光是不同的。

罗马记数与印度阿拉伯记数方法的不同，实质是单位化的差异。这种差异也反映在语言与文化方面。比如在英文中就没有“万”这个单位，“10000个1”用“10个千（Ten Thousand）”表达。凡此都说明“单位化”的眼光具有主观性，因而也就有了多样性。

图5 是数苹果过程中，将“2苹果”视为“单位”，得到算式“2苹果×3”。如果将“3苹果”视为“单位”，又会得到“3苹果×2”。

图6 单位化眼光

还可以把“4苹果”视为“单位”：

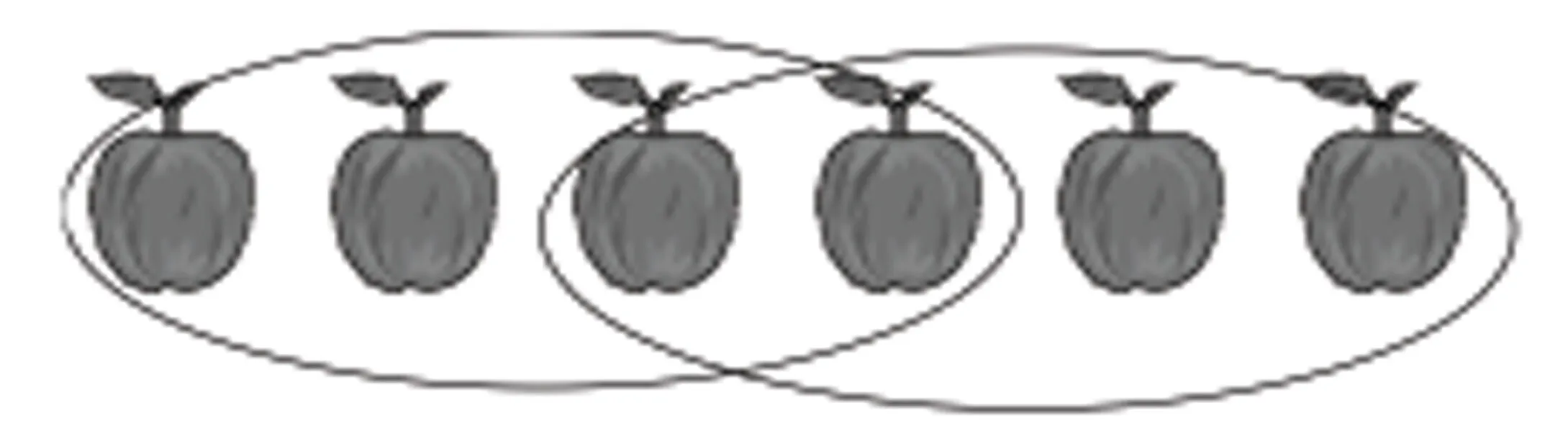
图7 重复示意图

此时如果用“4苹果×2”，出现了“重复”，也就是中间2苹果被使用2次，因此“4苹果×2=8苹果”就比实际苹果数多出2苹果，所以应当列出算式：4苹果×2－2苹果=6苹果。

如果将苹果的摆放方式改变为三角形形状，单位化的过程也会出现重复的情况。

图8 “三角形”排列示意图

把三角形一条边上的3苹果视为单位，每个顶点处的苹果就被重复利用，因此列出乘法算式“3苹果×3”，计算得到的9苹果中，有3苹果重复，因此还需要减去，即“3苹果×3－3=6苹果”。

因此，单位化眼光的差异，会带来算式和算法的差异，教师应当引导、鼓励学生运用异样和多样的眼光去观察。

综上，“乘”作为数学课程中的重要内容，其意义是动态的、发展的。认知起点并不限于“加”。乘的想法源于“单位化”的眼光，乘的运算在于实现单位转化，这样的想法从“数数”和“记数”的活动中就已经出现了。

随着数域的扩充，乘作为运算的算法和算理也会不断进化，但单位化的眼光和单位转换的意义将会继续沿用。计算教学仅关注算法和算理是不够的，更要关注背后的想法，特别是具有普遍意义的“大想法（Big Idea）”。像文中论及的“单位化”和“单位转化”这样的大想法，对于学生思维发展以及今后的数学学习都将起到重要作用。日复一日的日常教学，应当成为学生的想法逐步丰富与完善的过程。为学生设计的学习活动中，努力渗透这样的想法，应当成为教学研究的重要课题。