单站光测图像中空间目标姿态估计
2020-10-12杨小冈蔡光斌齐乃新马玛双
宋 平,杨小冈,蔡光斌,齐乃新,马玛双
(1.火箭军工程大学, 西安 710025; 2.中国人民解放军63768部队, 西安 710043)
空间目标监视系统,一般采用地基或天基探测设备对空间目标进行跟踪探测,获取目标的外形、尺寸、飞行轨迹、工作状态等信息,为民用和军用航天活动提供空间目标信息支援[1]。空间目标监视系统中地基光学设备具有测量精度高、投资成本低的优点,是空间目标监视系统重要探测手段之一。随着光电望远镜性能的提高和自适应光学技术的发展,地基自适应光学望远镜能够拍摄到空间目标的高分辨率图像。利用获取的光学图像数据,估计空间目标在飞行过程中的三维姿态,对分析目标实时状态、估计目标侦察区域、预测目标动作意图等方面的信息,具有重要意义。
目前,空间目标三维姿态估计方法大致可以分为两种:基于三维模型检索的方法和基于观测投影模型的方法。基于三维模型检索的方法,通常建立多视角卫星的二维姿态模型数据库,设计相应的特征匹配算法,将获取的目标图像特征与已建立的二维图像模型库中提取出的特征进行匹配,根据匹配结果估计出观测目标的真实三维姿态,如利用等积剖分网格建立模型数据库,通过几何特征提取和相似性匹配实现空间目标的三维姿态估计[2-4]。该方法需要建立庞大复杂的目标二维姿态模型数据库,需要掌握较多的目标先验信息,同时对硬件环境要求高,因此实际使用率较低。基于观测的投影模型方法,通常根据目标成像原理,建立二维图像和空间三维模型的某种特征投影关系,解算空间三维模型姿态,如使用光学或雷达传感器对目标进行跟踪观测获得目标图像,结合目标特征的投影成像关系,估计目标三维模型的姿态[5-7]。该方法需要准确建立投影关系,精确提取目标特征,实现难度较大。
在实际应用中,估计空间目标三维姿态主要目的是估计空间目标关键部件的空间指向,而且大多数空间目标存在明显的直线特征,例如卫星的太阳能帆板、卫星的主体轮廓。因此,本文提出了一种基于单站光测图像的空间目标姿态估计方法。通过建立目标三维模型,结合观测站观测空间目标的跟踪信息,获得空间目标仿真光测图像数据,采用Otsu阈值分割方法对图像进行目标和背景分割,利用LSD直线检测算法提取空间目标太阳能帆板的直线特征,采用面面交会方法解算出太阳能帆板中轴线在空间中的姿态,完成空间目标关键部件的指向估计。
1 三维姿态相关定义
1.1 目标三维姿态定义
在规定坐标系OXYZ中,空间目标的三维姿态参数包括俯仰角、偏航角和滚动角,分别定义如下:俯仰角α,目标特征轴线与坐标系水平面XOZ的夹角;偏航角β,目标特征轴线在坐标系水平面XOZ上的投影与OX轴的夹角;滚转角γ,目标绕中轴线旋转的角度,如图1所示。目标特征轴姿态指向可用单位矢量表示为
L=(cosαsinβ,cosαcosβ,sinα)T
(1)
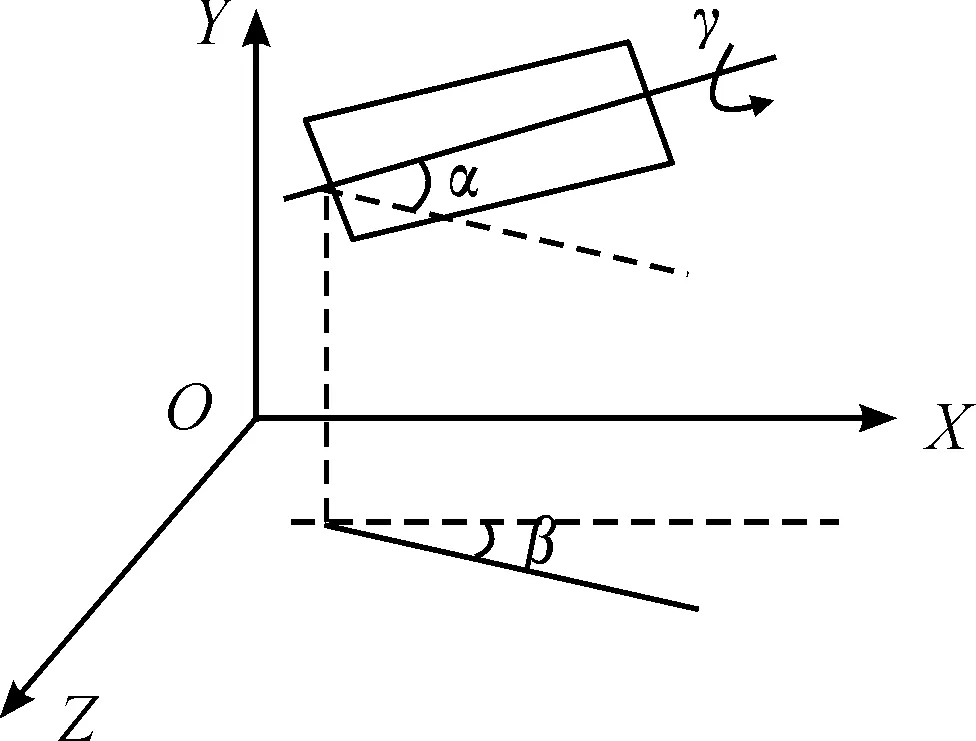
图1 目标特征轴三维姿态示意图
1.2 空间坐标系定义
地基光学望远镜对空间目标成像过程中,需要用到的坐标系主要有地球固定坐标系OXYZ、大地坐标系、测站坐标系OsXsYsZs、摄像机坐标系OcXcYcZc和图像坐标系o1x1y1。各坐标系的具体定义如下[8-10]:
1) 地球固定坐标系OXYZ。坐标原点O为地球质心,地球瞬时赤道面为基本平面,X轴在基本平面内由地球质心指向格林尼治子午圈;Z轴指向地球自转轴的瞬时北极,X、Y、Z满足右手定则。该坐标系固定在地球上,与地球一起自转。
2) 大地坐标系。观测站的站址坐标经常用大地坐标表示。该坐标系以大地参考为基准面,观测站的位置用λ、φ、h表示。大地经度λ,通过观测站的大地子午面与本初子午面的夹角。大地纬度φ,通过观测站的参考椭球面的法线与赤道面的夹角。大地高h,地面点沿法线到参考椭球面的距离。
已知测站原点用大地坐标系表示(λ,φ,h),则测站原点在地球固定坐标系下表示为(Xb,Yb,Zb),转换公式为
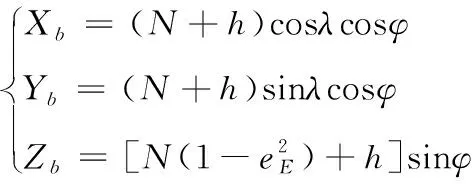
(2)
3) 测站坐标系OsXsYsZs。坐标原点Os为测站中心,即测量设备跟踪天线的旋转中心。站心当地地平面为基本平面。OsXs轴在基本平面内指向东方;OsYs轴指向大地正北方向;OsZs轴满足右手定则,与基本平面垂直指向上方。测站坐标系也称作测量坐标系。
根据测站坐标系OsXsYsZs的定义,测站坐标系OsXsYsZs与地球固定坐标系OXYZ的转换关系为
(3)
式(3)中,转换矩阵M为
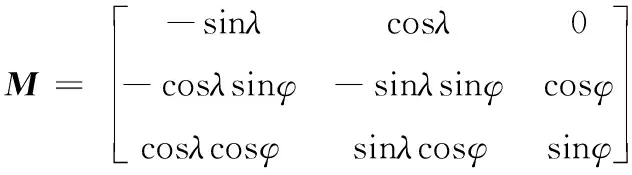
(4)
地基光学望远镜跟踪测量空间目标,就是在测站坐标系下测得目标的方位角A和俯仰角E,如图2所示。方位角A在测站坐标系中按顺时针方向从大地正北起算,俯仰角E从观测站当地地平面向上计量。ρ为目标到测站的距离,光学测量设备通常无法测得距离值。
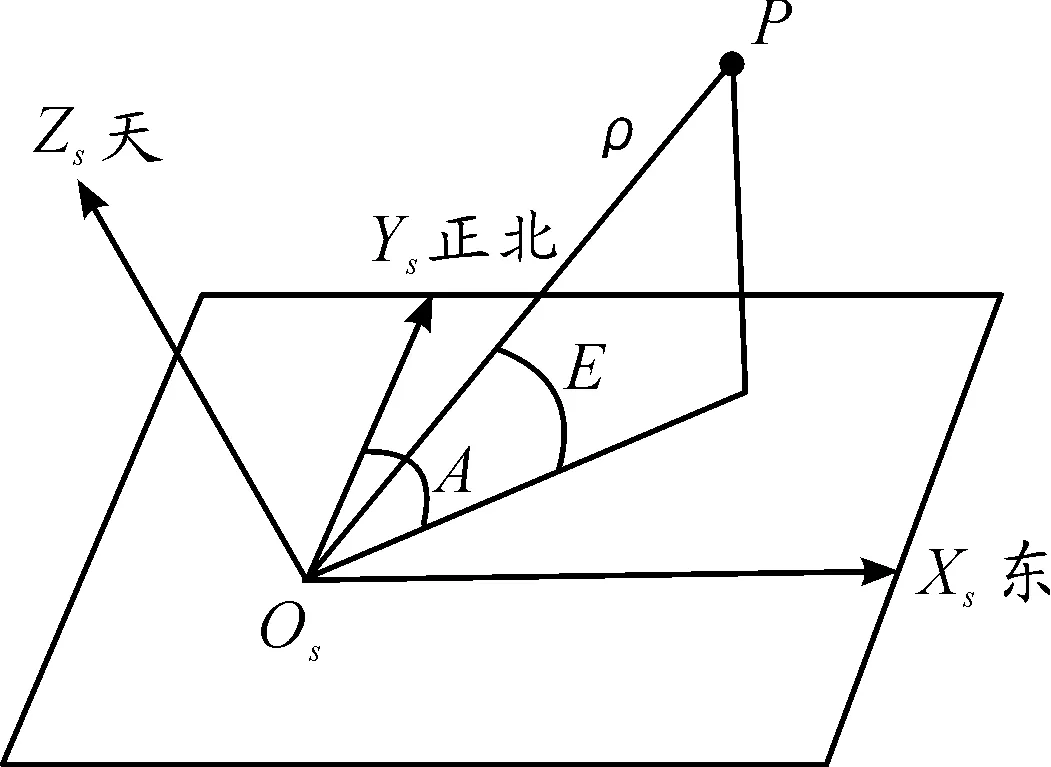
图2 测站坐标系示意图
4) 摄像机坐标系OcXcYcZc。坐标原点Oc为摄像机光心;Yc轴与摄像机的光轴重合,向前为正;Xc,Zc轴与下面图像坐标系的x1,y1轴平行。
5) 图像坐标系o1x1y1。图像坐标系o1x1y1是针对实时图成像所建立的二维直角坐标系,图像左上角点o1为坐标原点;x1,y1分别表示该像素在数字图像中的列数和行数。各坐标系的示意图如图3所示。
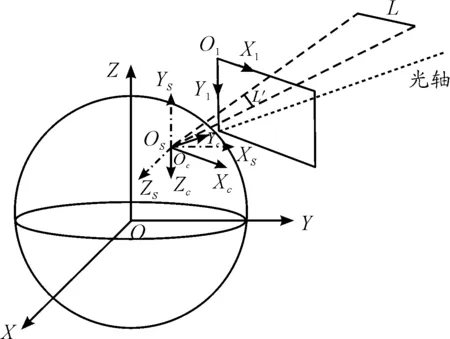
图3 各坐标系示意图
2 算法原理
本文提出的空间目标姿态估计方法利用地基自适应光学望远镜获得的空间目标图像数据,通过对图像数据预处理,提取目标图像的典型直线特征,结合测站成像关系,建立成像投影矩阵,估计目标直线特征在测站坐标系下姿态角参数α、β,从而完成目标直线特征指向的估计。同时利用测站坐标系和地球固定坐标系之间转换关系,能够实现目标直线特征在地球固定坐标系下的姿态估计。具体算法如图4所示,输入单帧图像经过图像预处理后,采用面面交会方法,估计目标特征轴在不同坐标系下姿态指向。
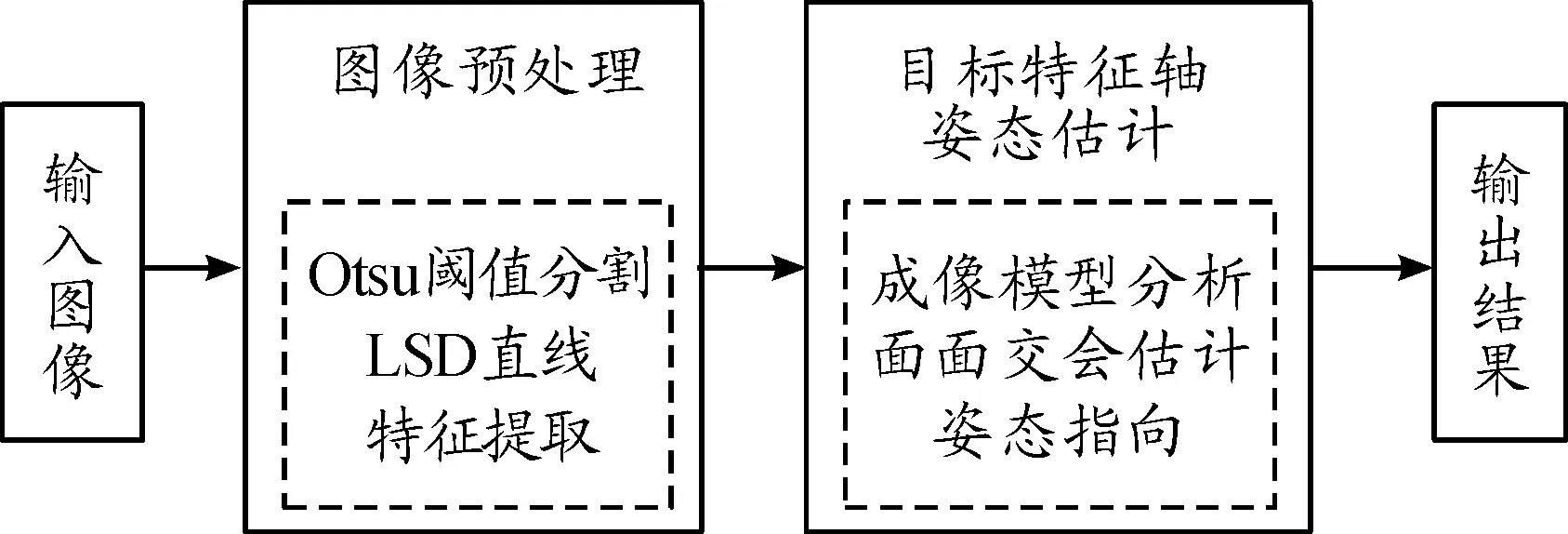
图4 目标特征轴姿态估计算法框图
2.1 图像预处理
地基光学望远镜拍摄空间目标图像主要是卫星。卫星的外形包含了较多直线特征,其中太阳能帆板最为明显,因此本文主要提取帆板直线特征。首先对图像进行目标和背景分割。由于空间目标图像的背景单一,目标与背景在灰度分布上差异明显,因此采用最大类间方差法(Otsu)阈值分割方法。Otsu阈值分割方法,通过选取一个最优阈值把原图像分为前景区域和背景区域,两部分的类间方差越大,说明两部分差别越大,便能有效的分割图像,选取最优阈值即为所求二值化阈值[11]。然后采用直线段检测算法(Line Segment Detector,LSD)提取图像数据上所有卫星的直线特征。LSD是一种直线检测分割算法,它通过寻找图像中梯度变化较大的像素,能够快速检测图像中的线段,同时使用了错误控制的方法,使得检测结果比较准确[12]。检测结果输出是线段的相关属性,比如线段的长度、线段两个端点坐标。由于卫星帆板的直线特征较为明显,因此通过LSD算法能够较为准确提取图像中卫星帆板的直线。
2.2 成像模型分析
摄影机模型采用中心透视投影成像模型。假设空间中任意一点P,其在测站坐标系中的坐标(Xs,Ys,Zs),在摄像机坐标系中的坐标(Xc,Yc,Zc),在图像坐标系中的坐标(u,v),则测站坐标系、摄像机坐标系、图像坐标系的关系如下[13]:
(5)
(6)
式(5)中:R是摄像机旋转矩阵;T是摄像机平移向量;式(6)中,f为摄像机焦距;s为倾斜因子;Cx,Cy为摄像机主点;α为图像像素纵横比。一般假设s=0,α=1,式(6)简化为摄像机内参数的三参数模型[14]。
在测站坐标系下,由于坐标系的平移并不影响目标中轴线指向,因此直接假设摄像机坐标系原点与测站坐标系原点重合。测站坐标系、摄像机坐标系、图像坐标系的转换过程式(5)和式(6)简化如下:
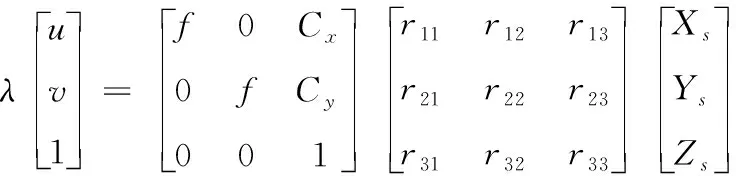
(7)
光电望远镜光轴上任意一点P的方位角和俯仰角分别是A、E。图5表示摄像机坐标系和测站坐标系的变换关系。摄像机旋转矩阵R为[15]:
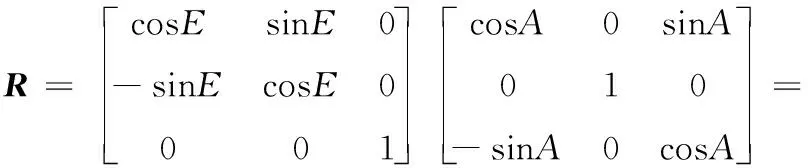

(8)
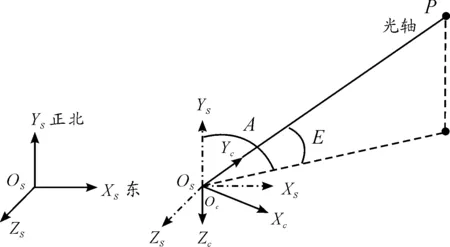
图5 摄像机坐标系与测站坐标系的关系示意图
2.3 面面交会估计姿态指向
太阳能帆板有两组相互正交的平行线,利用单幅图像中帆板两条平行长边,进行面面交会,计算帆板中轴线的姿态指向。如图6所示,帆板的两条平行长边为直线L1和L2,帆板的中轴线为直线L,L1和L2所成的像分别是l1和l2,l1和l2分别与光心C确定平面Π1和Π2。平面Π1和Π2交会得到空间直线L′,通过两个空间平面方程联立描述空间直线,即为面面交会确定空间直线。根据几何知识,平面Π1和Π2的交线L′平行于中轴线L,两者的姿态角一致。因此,求得Π1和Π2的交线L′的俯仰角和偏航角,就是中轴线L的姿态角。
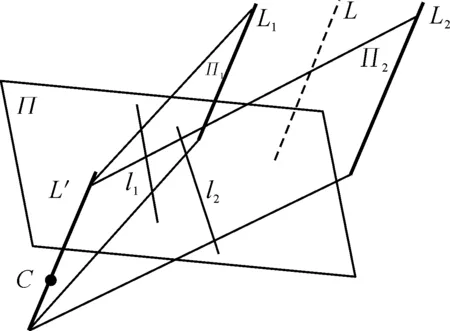
图6 面面交会求帆板中轴线姿态角原理示意图
图像上l1和l2的直线方程表示为
aiu+biv+ci=0 (i=1或2)
(9)
其中,i=1表示l1直线方程,i=2表示l2直线方程。将式(7)代入式(9),得
AiXs+BiYs+CiZs+Di=0 (i=1或2)
(10)
式中,i=1表示Π1平面方程,i=2表示Π2直线方程,
Ai=aifr11+aiCXr31+bifr21+biCyr31+cir31
Bi=aifr12+aiCXr32+bifr22+biCyr32+cir32
Ci=aifr13+aiCXr33+bifr23+biCyr33+cir33
由此得出平面Π1和Π2的交线L′的方程为
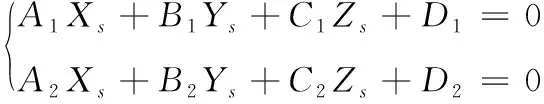
(11)
其矩阵表示形式为
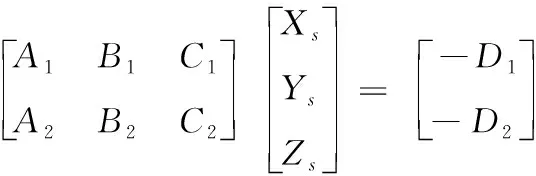
(12)

姿态角为
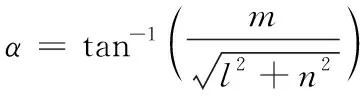
(13)
(14)
由于直线L平行于直线L′,利用式(13)和式(14)求得测站坐标系下直线L空间指向式(1),即目标中轴线姿态指向。
在地球固定坐标系下,将测站坐标系OsXsYsZs与地球固定坐标系OXYZ的转换关系式(3),代入交线的式(12),得
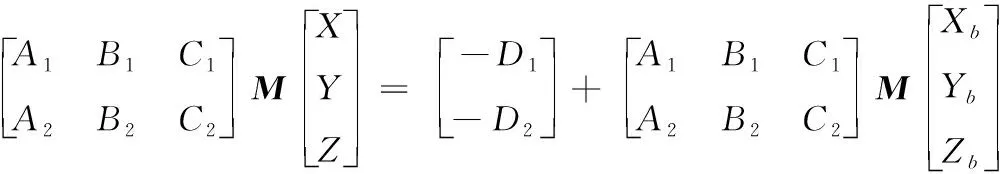
(15)

2.4 本文算法结构流程
本章提出采用单站光测图像估计空间目标姿态参数,算法流程如图7所示,首先采用Otsu阈值分割方法对图像进行目标和背景分割,利用LSD直线检测算法提取卫星太阳能帆板的直线特征;然后建立摄像机投影成像关系,通过面面交会方法,完成目标特征轴在不同坐标系下姿态角估计和指向预测。
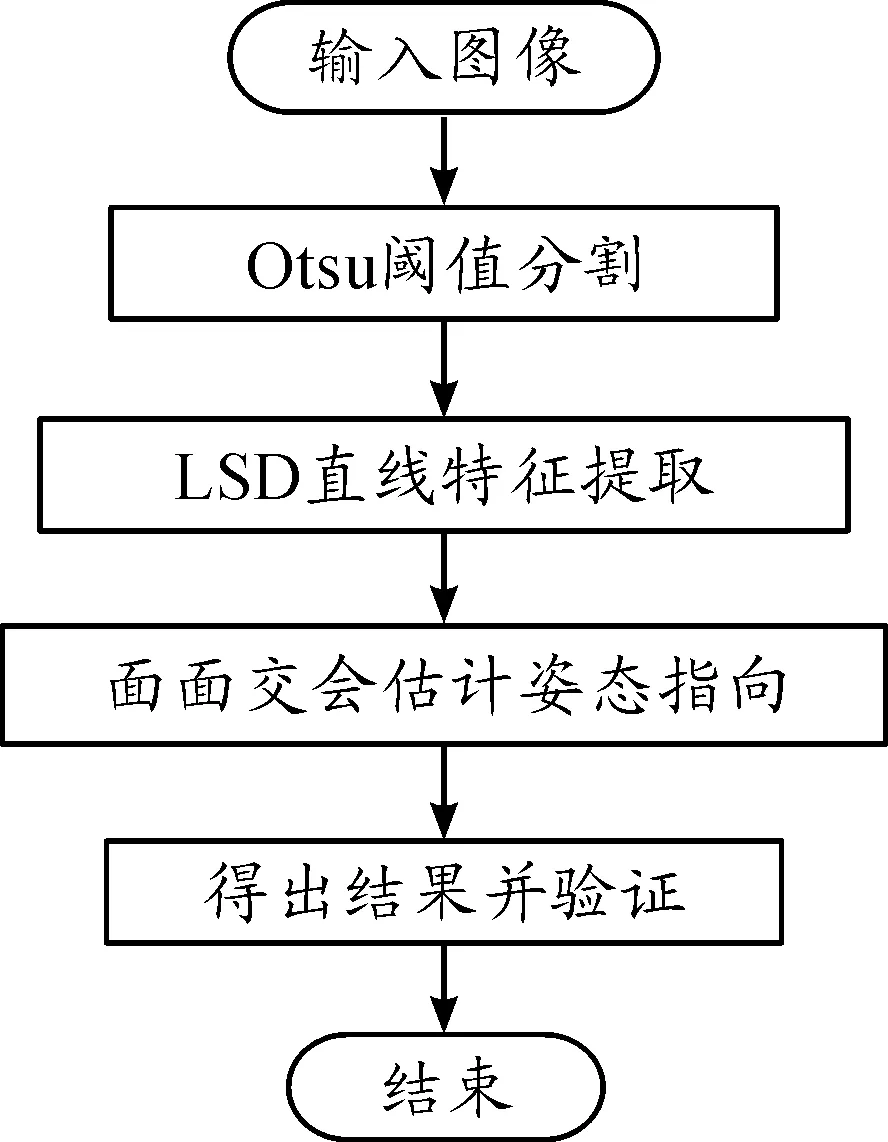
图7 目标特征轴姿态估计算法流程框图
3 仿真实验分析
3.1 实验结果
本文采用XX型号卫星三维模型作为仿真观测及姿态估计实验的空间目标。通过建立目标三维模型,结合实际观测弧段的观测时刻、测站方位和太阳光照,模拟空间目标成像过程,获取空间目标在轨姿态。为了提高光学系统分辨力,地基光学探测设备通常使用长焦距摄像机,假设摄像机焦距f=1 m。已知观测站观测不同姿态目标的方位角和俯仰角,观测站的站址位置经度108.95°,纬度34.27°。按照2.4节算法流程对卫星太阳能帆板中轴线的姿态进行估计。具体不同姿态的仿真图像如图8所示。
模拟观测图像需要采用Ostu阈值分割方法对空间目标与背景进行分割,得到去除背景后的空间目标二值图像。利用LSD直线提取算法提取二值图像上卫星的大部分直线特征,但其中只有帆板直线特征用于后续姿态估计。因此,通过提取直线的长度、斜率和端点坐标作为约束条件,对LSD算法提取的结果进行了筛选,筛选结果中只保留了帆板四周的直线,而其余直线特征被剔除。如图9所示,不同姿态下图像处理结果,图9(b)表明Ostu阈值分割方法能够较好分割空间目标和背景,图9(c)表明LSD直线特征提取算法能够准确、稳定提取卫星的大部分直线特征,图中绿色直线是通过提取直线约束条件筛选出帆板四周的直线。
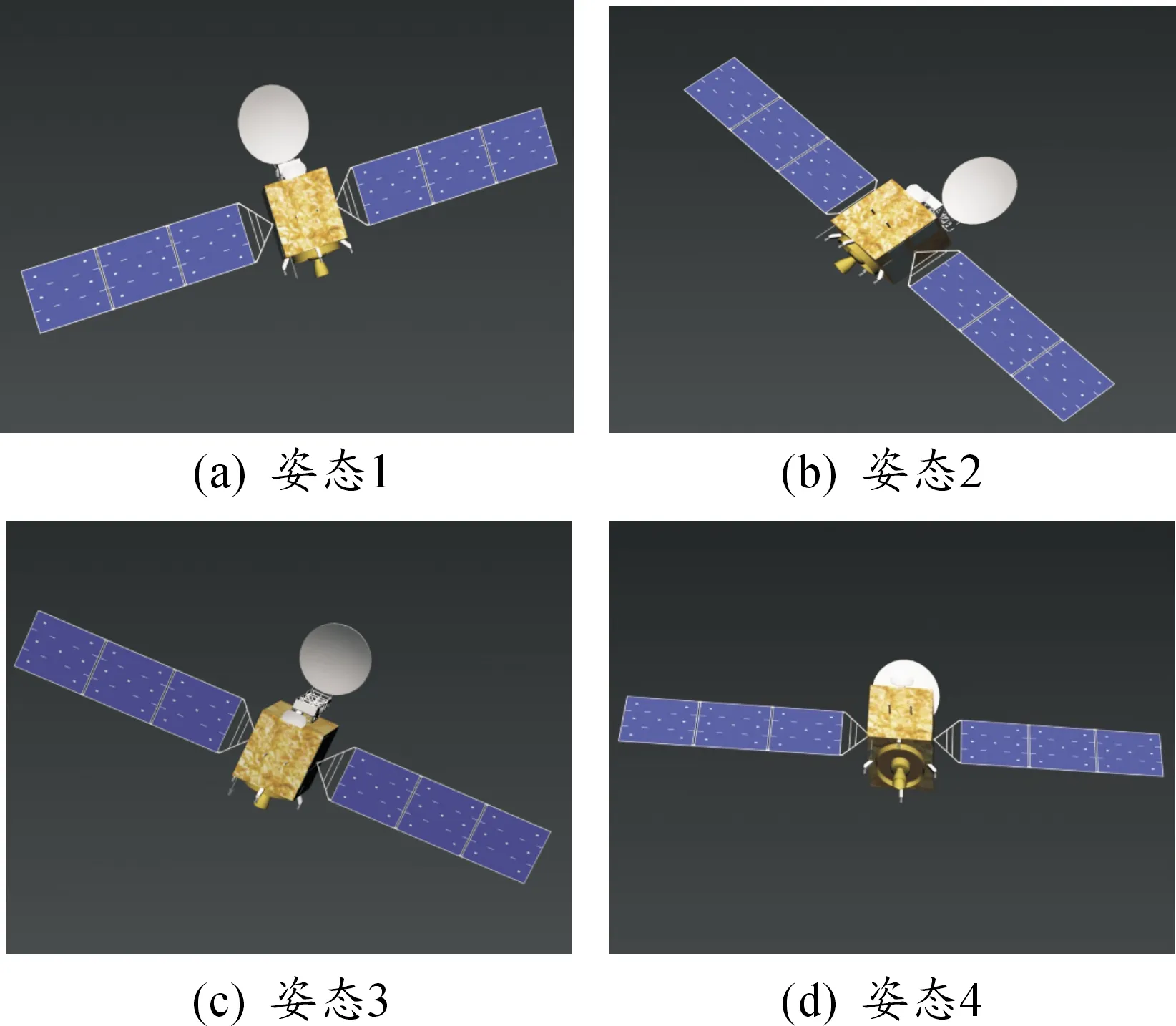
图8 不同姿态的仿真图像
结合已知信息,按照2.3节的方法求得在不同坐标系下不同姿态的卫星帆板中轴线姿态角和指向,如表1所示。表中,测站观测信息是地基光学望远镜跟踪测量空间目标时在测站坐标系下测得目标的方位角A和俯仰角E,具体定义见1.2中测站坐标系。特征轴三维姿态角是卫星太阳能帆板中轴线在测站坐标系下俯仰角和偏航角,具体定义见1.1。测站坐标系下空间指向式(1)直接通过式(12)交线方程解得;地球固定坐标系下空间指向式(1)通过式(15)交线方程解得。从表1可以看出:利用本文方法能够实现卫星太阳能帆板中轴线在不同坐标系下的三维姿态角和空间指向的估计。
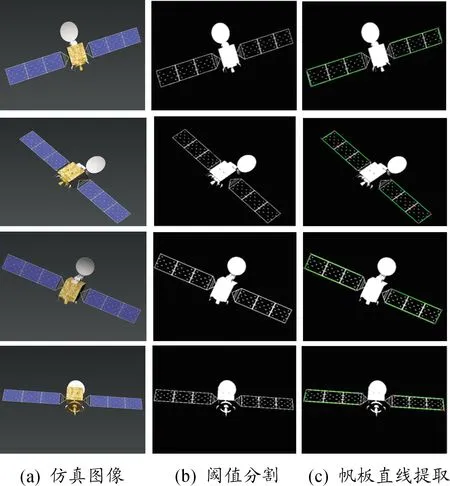
图9 不同姿态下处理后的图像
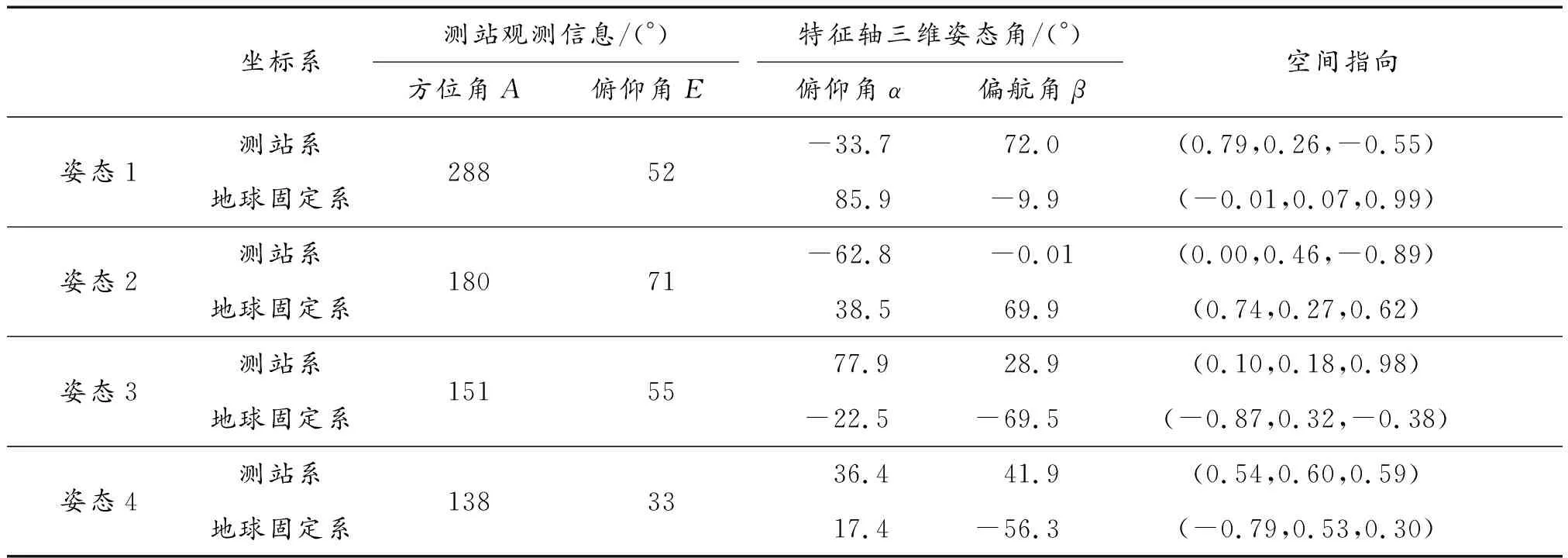
表1 卫星帆板中轴线姿态角和指向
3.2 验证分析
为了验证姿态估计结果的准确性,引入目标本体坐标系OtXtYtZt,Xt为帆板中轴线指向,Yt为垂直于帆板中轴线指向上,Zt由右手定则确定。目标本体坐标系与测站坐标系的关系如图10所示,α为目标的俯仰角,β为目标的偏航角。目标本体坐标系与测站坐标系的转换关系为
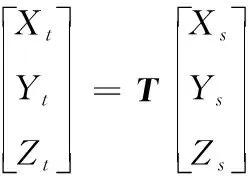
(16)
式(16)中,转换矩阵为

(17)

图10 目标本体坐标系与测站坐标系关系示意图
通过2.3节方法求解在测站坐标系下帆板短边的中轴线,如图11所示直线L″。已知目标本体坐标系与测站坐标系的转换关系式(16)和式(17),代入3.1节估计的姿态角α、β,则求得L″在目标本体坐标系下空间直线方程为
(18)

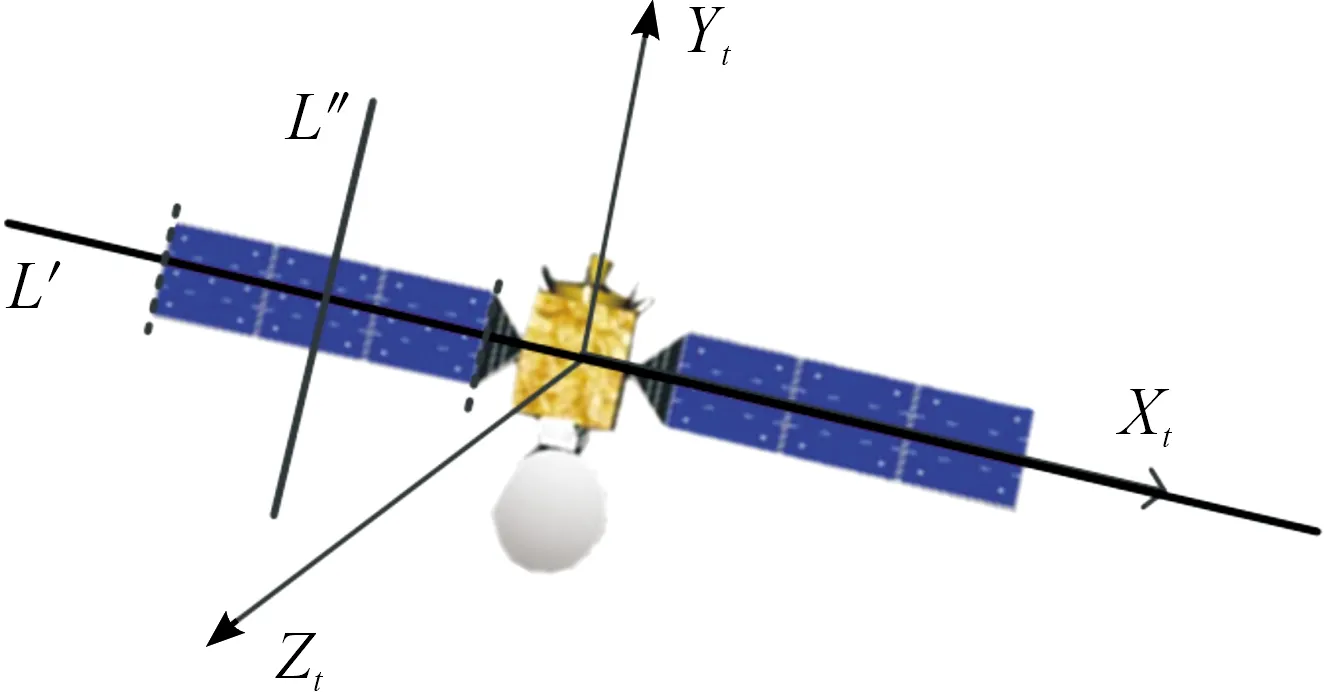
图11 帆板短边的中轴线示意图
由于目标本体坐标系定义Xt为卫星帆板长边中轴线指向,如图11所示直线L′,通过判断直线L′和L″是否垂直,验证本算法帆板中轴线指向估计的精度。按照上述方法代入实验数据求得L″与Xt轴的夹角,计算结果见表2。

表2 计算结果
从验证结果可以看出:在目标本体坐标系下直线L″与Xt轴的夹角接近90°,即直线L′和L″基本垂直,因此本方法估计卫星帆板中轴线指向结果较为精确。
4 结论
利用空间目标太阳能帆板直线特征,结合测站跟踪观测空间目标的信息,提出了一种基于单站光测图像的空间目标姿态估计方法。通过仿真验证,该算法能够解算出空间目标帆板直线特征在指定坐标系下的姿态,实现指向估计。
