独立微网逆变器VSG控制惯量阻尼系数自适应研究

高明宇，刘金宁，冯长江

(陆军工程大学石家庄校区 车辆与电气工程系, 石家庄 050003)

随着全球能源危机不断加深，新能源技术日趋成熟，更加灵活、智能，可靠性更高的微电网系统受到越来越多的关注[1]。其中，新能源并网逆变器是连接新能源分布式电源与同步发电机的关键环节，其控制方法的选取对于系统的稳定性有着重要影响[2-3]。虚拟同步机控制方法(Virtual Synchronous Generator,VSG)能够表现出发电机组的惯性特性和阻尼特性，得到广泛应用[4]。不同于传统发电机组，VSG控制中惯量和阻尼系数不受物理结构限制，取值更加灵活，具有更好的工程应用特性[5-6]。

针对VSG控制的惯量和阻尼参数优化控制，文献[7-10]采用转动惯量和阻尼系数自适应调节控制策略,能够在负载变化时抑制系统频率波动，从而提高稳定性，但以上研究主要针对单一逆变器输出系统，没有分析并联系统，且只涉及频率稳定，在功率调控方面没有提及。文献[11]针对双机并联系统，将负载变化的暂态过程分为两个阶段逐段分析，并提出一种基于虚拟电感和暂态阻尼的暂态主动功率分配优化方法，改进了暂态有功分配的动态性能，但是文献中方法需要并联微源的准确信息，且只改进了阻尼系数，对于惯量系数分析不足。文献[12]提出了一种基于分布式通信架构的互阻尼控制策略，通过相邻VSG间的互阻尼控制来抑制功率震荡，但是这一控制方法引入通信线路和上级控制，增加了系统的复杂程度。文献[13]利用等效同步发电机原理，提出了虚拟同步发电机多机并联运行的虚拟惯量匹配方法，但文献中只研究稳态功率分配问题，对于稳定性问题没有涉及，同时也需要并联微源的准确参数，自适应能力不强。

独立微网运行时，各微源间功率波动和分配不均是影响稳定性的重要因素。对此，本文通过采集不同阶段的系统功率波动差值和频率变化率，采用微网惯量、阻尼系数自适应方法，逐步消除功率分配不均现象，并通过Matlab/Simulink进行仿真验证。该方法不需要明确并网的发电机组各个参数值，具有较强的自适应能力。

1 惯量、阻尼系数特性分析

传统VSG控制运动方程：

(1)

其中：Pm为虚拟原动机输出的机械功率；Pe为输出的电功率；J0为惯量系数；D0为阻尼系数；ω为转子转速；ω0为同步角速度[14]。

典型虚拟原动机的功频表达式为式(2)：

Pm=Pn+Kω(ω0-ω)

(2)

其中：Pn为有功功率额定值；Kω为功频调差系数。由式(1)可得：

(3)

J、D为惯性、阻尼分量，s为微分算子，与惯量、阻尼系数关系为式(4)：

(4)

在稳态时，根据终值定理可得式(5)[15]：

(5)

传统下垂控制的功频特性方程为

ω=ω0+kp(Pn-P)

(6)

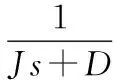
为进一步分析系统参数的影响，将分布式电源简化建立并联系统小信号模型如图1所示[16]。

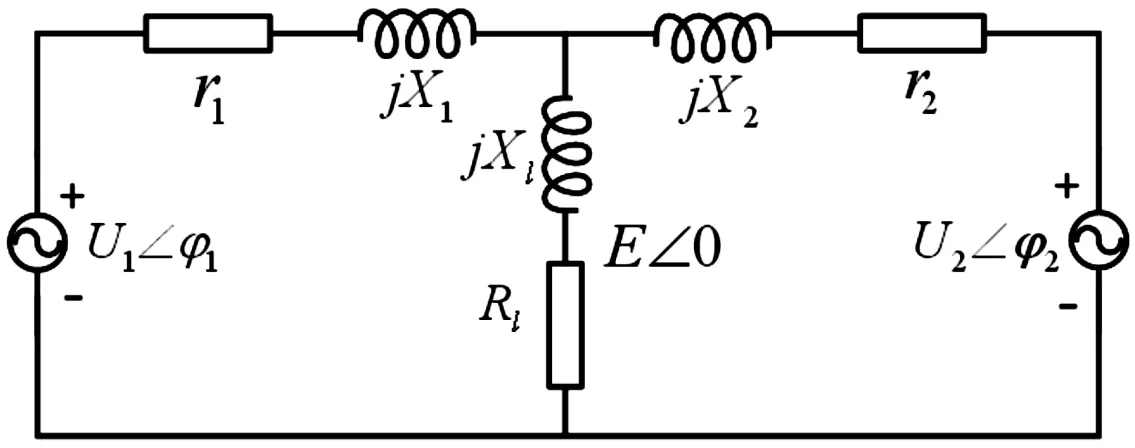
图1 微源并联系统模型结构示意图

其中，其中E∠0为交流母线电压，并设定相角为零，δi为VSG控制逆变器与发电机组的相角差，Ui∠δi(i=1,2)为各微源的逆变器输出电压值，Zl为并联系统的公共负载，Zi(i=1,2)分别为逆变器和发电机组的输出阻抗。

以图2所示系统建立小信号模型。文献[17]的方法，以功频特性方程为基础，建立系统的小信号模型：

(7)

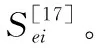
s3+As2+Bs+C=0

(8)

其中：

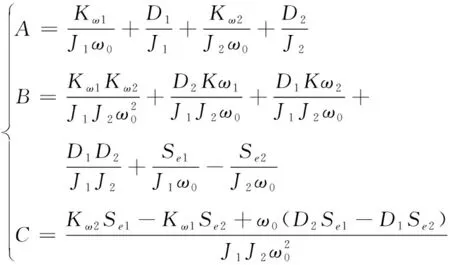
(9)

结合式(7)、式(8)、式(9)，假设微源U1∠δ1为发电机组，其惯量系数、阻尼系数值恒为定值，U2∠δ2为VSG控制逆变器，通过改变参数值，系数根轨迹变化如图2所示。

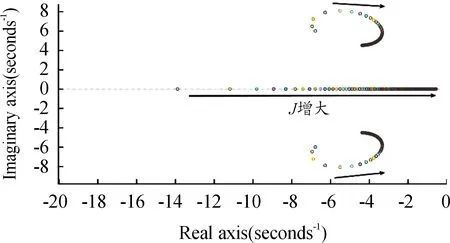
图2 惯量系数根轨迹变化图

(D1=D2=6，J1=1.2,J2=0～20)

由根轨迹图3可知：当J1=J2=1.2时，系统为近似二阶系统，特征根远离虚轴，稳定性最佳，随着参数值的继续增大，系统逐渐由近似二阶系统变为一阶系统，特征根逐渐逼近虚轴，稳定性降低。同理可得当D1=D2=6时系统的稳定性最好，并随着参数值增加，系统稳定性降低。因此当并联系统的惯量、阻尼系数一致时，系统稳定性最佳。由于系统参数相同时，功率分配的暂态及稳态特性趋于一致，能够减少功率环流及过冲，有利于系统稳定，这与参数小信号分析的结果一致。

图3 阻尼系数根轨迹变化图

(J1=J2=1.2，D1=6,D2=0～50)

2 自适应惯量、阻尼控制原理

由式(1)可得：

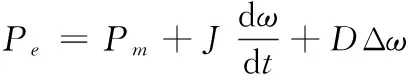
(10)

根据式(10)，设Pe1和Pe2分别为两个微源的输出功率，则有:

(11)

为简化分析，设并联微源的功频下垂系数及容量一致，当系统并联运行时，忽略线路阻抗，则有:

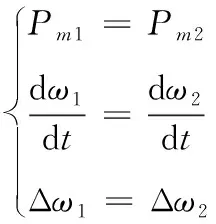
(12)

根据式(11)、式(12)，可知：

(13)

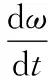
图4 惯量阻尼自适应控制框图

(14)

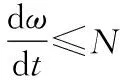
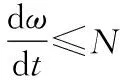
Pe1-Pe2≈(D1-D2)Δω

(15)

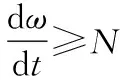
(16)

3 仿真验证

将以上内容通过Simulink进行仿真。仿真参数如表1、表2所示。

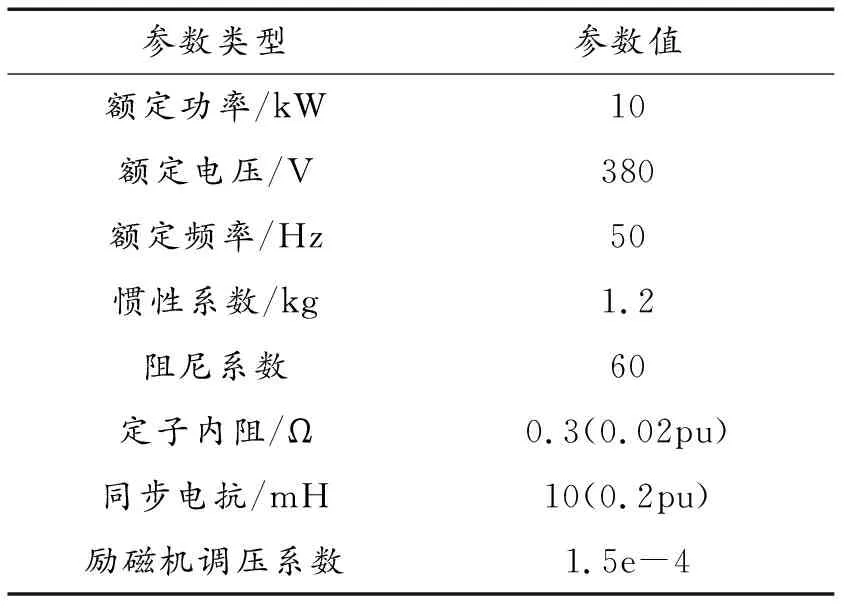
表1 发电机组参数

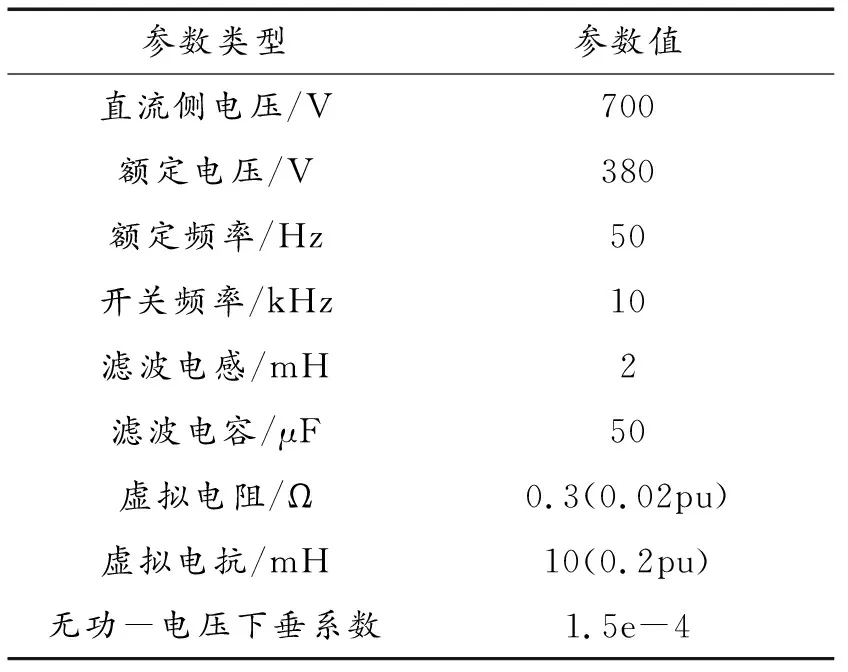
表2 逆变器控制参数

仿真以典型工况为例，区分并网和独立运行两种情况。并网运行中，预同步后在0.5 s切入大电网，1 s时加入5 kW负载，负载由2 s时切除负载并断开并网开关。独立运行时，并联运行的工况设置如下：新能源逆变器带8 kW负载运行，达到设置负载上限，空载启动发电机组，在0.2 s时，打开预同步环节[18]，在0.5 s时打开并网开关，逆变器与发电机组并联运行，1 s时加入5 kW负载，2 s时切除。3 s加入7 kW负载，4 s大负载切除，并联开关断开，新能源逆变器独立带7 kW负载继续运行。其中逆变器分别采用下垂控制、VSG控制和自适应系数控制，观察各微源有功功率输出波动情况。

由图5及数据分析可以看出，在并网运行时，系统的功率分配稳定有效。在独立运行中，采用各控制方法输出波形的数值对比如表3所示。如图6所示，采用下垂控制时，系统调节速度较快，但是在负载功率波动时，微源的输出功率不平衡。如图7所示，采用定参数VSG时，系统功率波动较大，稳定时间长。如图8所示。采用自适应惯量阻尼控制时，相较于定参数VSG控制，系统功率波动减小79%，稳定时间缩短31%，相较于下垂控制明显消除功率波动偏差，且稳态偏差减小25%。由此可以看出自适应惯量阻尼控制具有一定的优越性。如图9所示。系统完成自适应过程后，VSG控制的惯量和阻尼系数分别为J=1.17，D=6.16，与发电机组设定参数(J=1.2，D=6.08)相近。存在误差的原因为系统的惯量阻尼系数存在一定的耦合，分段控制可以减少这一偏差，但是不能完全消除。

图5 微网并网运行功率图

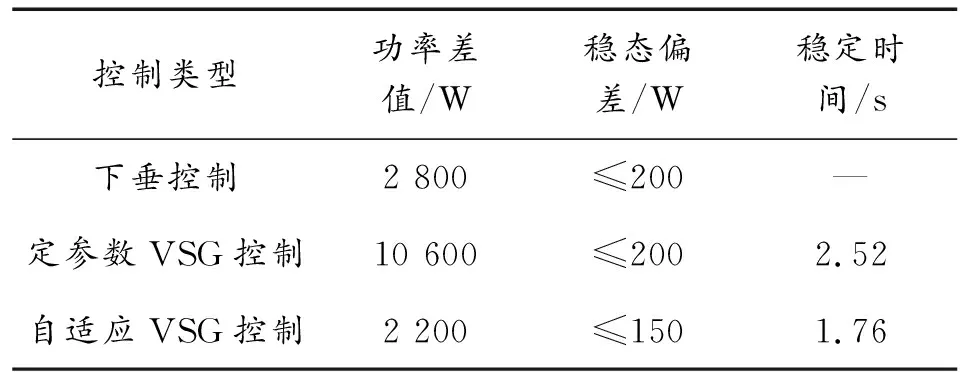
表3 控制输出波形参数

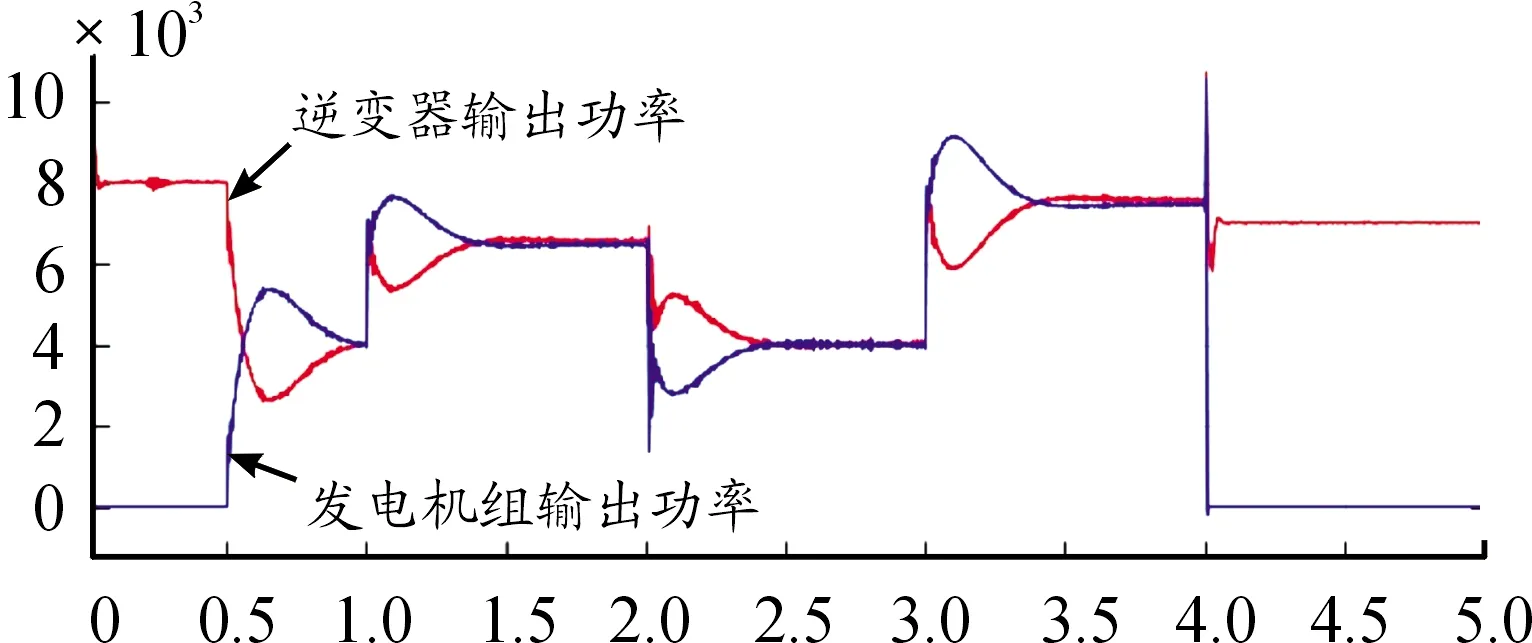
图6 下垂控制逆变器-发电机组并联功率图

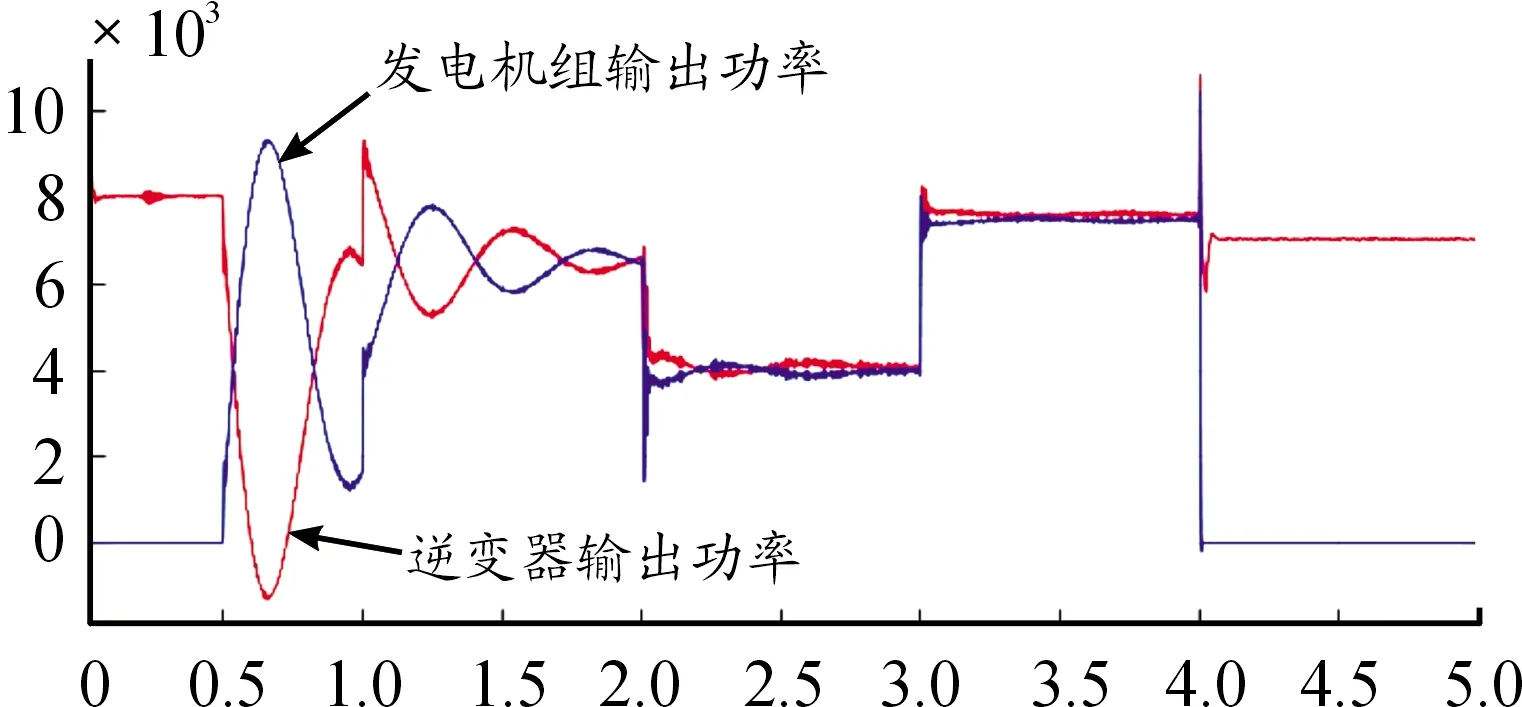
图7 固定惯量阻尼系数逆变器-发电机组并联系统模型

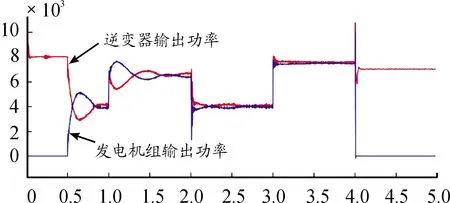
图8 自适应惯量、阻尼系数控制逆变器-发电机并联功率图

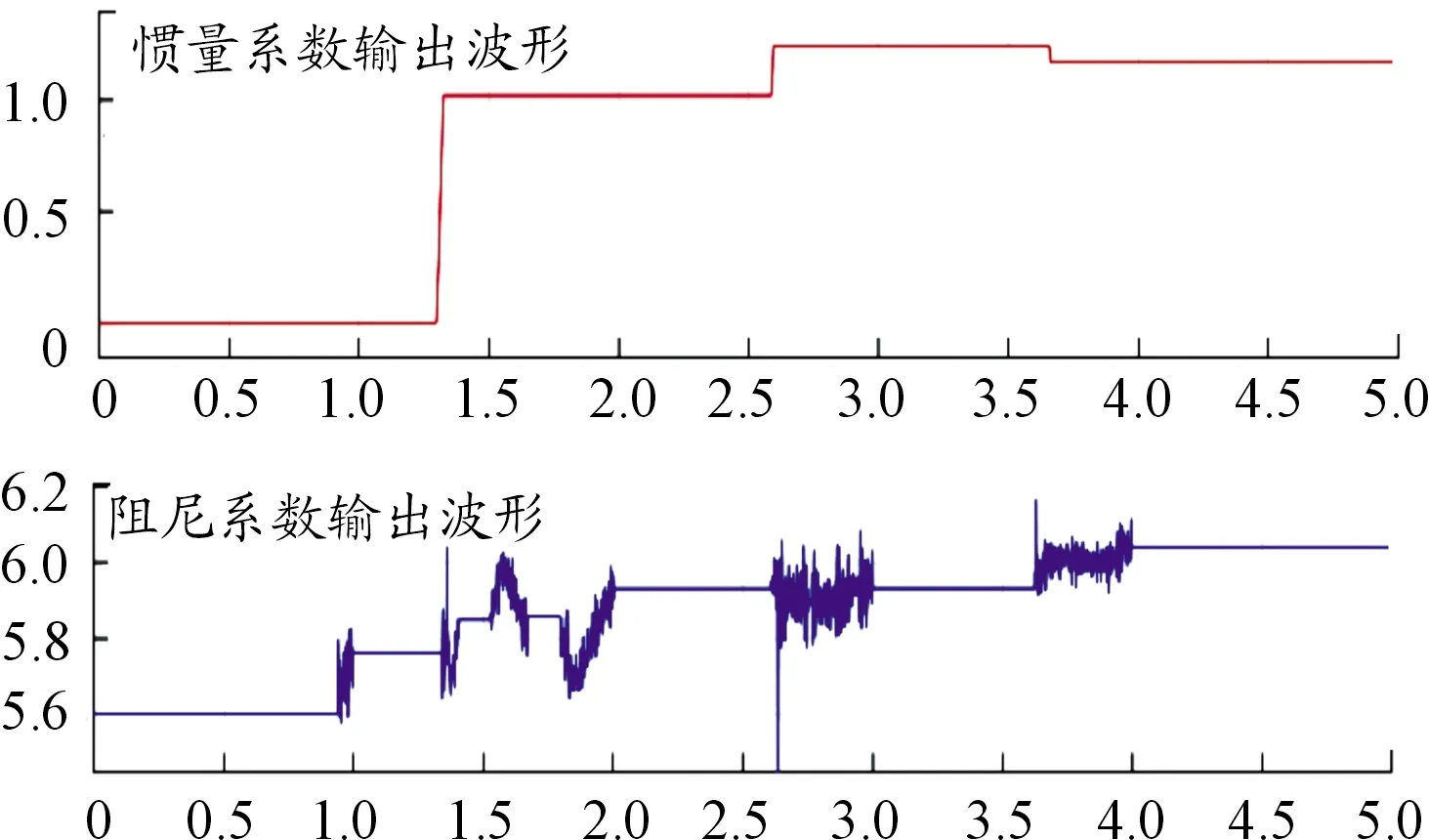
图9 自适应惯量、阻尼系数输出波形

4 结论

本文针对独立微网中发电机组-逆变器双机并联系统的功率波动问题，提出了采用分段自适应惯量、阻尼控制方法，提升系统整体性能，并在Matlab/Simulink上对该方法进行了仿真实验。结果表明：相较于传统下垂控制并联和固定参数并联而言，该方法功率波动和稳态误差更小，系统的稳定时间更短，该方法不需要明确发电机组的惯量和阻尼系数，能够实现和任意机型的发电机组稳定并联，克服了传统并联逆变器使用场景单一的缺陷，自适应性较强。